基于距离模型的动态直觉模糊多属性决策方法

梅晓玲

(郧阳师范高等专科学校数学与财经系，湖北 十堰 442000)



基于距离模型的动态直觉模糊多属性决策方法

梅晓玲

(郧阳师范高等专科学校数学与财经系，湖北 十堰 442000)

针对已知各决策时段的时间权重，以直觉模糊数形式给出的动态多属性决策问题，利用直觉模糊加权算子对各时段的评价值进行集成，得到综合评价值，同时构建直觉模糊集的记分函数，充分考虑和挖掘直觉模糊犹豫指数部分的信息，以提高对直觉模糊数评价的准确性。利用记分函数确定直觉模糊多属性决策指标集的正负理想点，避免采用绝对优的点或绝对劣的点进行评价引起偏差，并由此构造基于距离公式的排序模型，对整个方案集进行排序并择优。最后利用实例验证该方法的实用性与可行性。

动态多属性决策；直觉模糊数；直觉模糊数加权算子；记分函数

引 言

模糊多属性决策问题在人们的日常生活及工作中普遍存在，由于客观事物的复杂性、不确定性，以及决策者思维的模糊性，在决策中，数据往往难于给出精确数值而以模糊数的形式给出，即模糊决策问题。目前，对于模糊多属性决策问题研究较为突出的是单时段的模糊决策问题，如以区间数、三角模糊数、vague集和直觉模糊数为属性值的单时段模糊多属性决策问题。但在许多属性评价实践中，存在多时段的模糊决策问题，如：多时段投资决策、军事系统有效性动态评价以及医疗诊断等都需要引进决策时段，进行动态评价。

目前动态模糊多属性决策问题的研究已成为决策领域研究的热点[1-8]，主要的思想方法是将传统的多属性决策方法如TOPSIS、VIKOR、灰色关联法等思想拓展应用到动态多属性决策问题中，对这类问题的解决也提供了许多决策思路。在此基础上，本文针对各决策时段的时间权重已知，属性值以直觉模糊数形式给出的动态多属性决策问题，首先利用直觉模糊加权算子对各时段的评价值进行集成，得到综合评价值，同时，引入记分函数，利用记分函数思想确定直觉模糊多属性决策指标集的正负理想点，这样最优点与最劣点更贴近实际，避免采用绝对优的点(1,0,0)或绝对劣的点(0,1,0)进行评价引起偏差，并由此构造基于距离公式的排序模型，对整个方案集进行排序并择优。

1 基本理论

1.1 直觉模糊数的定义

集合A：A={|x∈X}的三重组称为A是X上的一个直觉模糊集，其中函数：μA:X→[0,1]和vA:X→[0,1]，且满足0≤μA(x)+vA(x)≤1(∀x∈X)，称μA(x),vA(x)分别为X上元素x属于A的隶属度和非隶属度，令πA(x)=1-μA(x)-vA(x)是x对A的犹豫程度。为方便起见，直觉模糊集也可表示为A=<μA(x),vA(x)>。

直觉模糊集最大的特点就是同时考虑隶属和非隶属两方面的信息，这使得直觉模糊集在处理不确定信息时比传统的模糊集有更强、更准确的表示能力，且更灵活。

1.2 直觉模糊集之间的距离

设

A={|x∈X}

B={|x∈X}

Euclidean距离[9]：

EIFS(A,B)=

Hamming距离[10]：

HIFS(A,B)=

1.3 记分函数的概念

记分函数思想是用函数将直觉模糊集转化成具体数值并确定直觉模糊集的优劣关系，这样筛选出的最优直觉模糊点与最劣直觉模糊点作为标准计算会更贴近实际，避免采用绝对优的点(1,0,0)或绝对劣的点(0,1,0)进行评价引起片面性。直觉模糊集已有记分函数主要有：

Chen和Tan提出的记分函数[11]：

S(E(Ai))=uAi-vAi

Hong和Choi提出的记分函数[12]：

H(E(Ai))=uAi+vAi

刘华文就“投票模型”进行分析提出新的记分函数[13]：

L(E(Ai))〗=uAi+(1-uAi-vAi)uAi

1.4 动态直觉模糊加权平均算子[14]

为动态直觉模糊加权平均算子(DIFWA)。

2 动态直觉模糊多属性决策方法

一个具有p个不同时段tk(1,2,...,p)的动态直觉模糊模糊多属性决策问题可以定义为：

ω(t)=(ω(t1)，ω(t2)，…，ω(tp)),i=1,2,…m

基于距离模型的动态直觉模糊多属性决策问题，已知的是各时段的直觉模糊数决策矩阵(假设均为效益型指标)、各时段的时间权重，通过一定的方法对各方案进行决策。决策过程如下：

步骤1 利用DIFWA算子集成得到直觉模糊综合评价矩阵。将p个不同时段的直觉模糊数决策矩阵

利用动态直觉模糊加权平均算子(DIFWA)集成得到直觉模糊综合评价矩阵：

这里

此记分函数充分考虑和挖掘了直觉模糊犹豫指数(不确定)部分的信息，提高对直觉模糊数评价的准确性，同时也可避免选择绝对优点(1,0,0)和绝对劣点(0,1,0)对决策问题带来计算偏差，这样筛选出的最优点与最劣点作为标准计算更贴近实际。

步骤3 构造基于直觉模糊数距离公式的排序模型，得到各方案的排序值并进行择优。

i=1,2,...,m

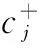
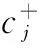
3 实例分析

某金融投资公司拟对4个备选企业(方案)xi(i=1,2,3，4)进行资金投资，制订了4项评价标准(属性)：企业经济价值(c1)、企业社会价值(c2)、企业员工幸福指数(c3)和企业环境污染程度 (c4)。现由投资公司领导团队对每个企业在4个不同时段的各项属性进行评价，评估信息经过统计处理后，得到直觉模糊决策矩F(t),t=1,2,3,4，见表1～表4。根据各时段外界因素的干扰程度确定时间权重为ω1=0.11，ω2=0.21，ω3=0.31，ω4=0.37，试以确定最佳的投资对象。

表1 直觉模糊决策矩阵F(1)

表3 直觉模糊决策矩阵F(3)

表4 直觉模糊决策矩阵F(4)

c+=((0.72，0.12，0.16),(0.79，0.13，0.08),(0.88，0.09，0.03),(0.82，0.12，0.06))

最劣属性值序列为：

c-=((0.70，0.21，0.09),(0.68，0.21，0.11),

(0.52，0.38，0.10),(0.74，0.21，0.05))

(3)由直觉模糊数距离公式排序模型计算各方案的S(xi)值：

S(x1)=1.4464

S(x2)= 2.7222

S(x3)=4.5600

S(x4)=1.0952

方案的排序为：x3>x2>x1>x4。

由距离模型计算得到的排序结果符合实际情况，企业3的各项指标在四个时段均表现较优，是最值得投资的企业，而企业4的指标1、2、4时段表现较差，由模型计算的综合结果也显示该企业整体可投资水平不高的现状。从实例可以看出，由该模型计算的排序结果分辨率较高，结果符合实际，从而为动态直觉模糊多属性决策问题提供一种新的决策思路。

[1] 杨威,庞永锋.一个基于不确定动态几何加权平均算子的多属性决策方法[J].数学的实践与认识,2011,41(8):45-49.

[2] 张世芳.几种模糊多属性决策方法及其应用[D].西安:西安电子科技大学,2012.

[3] 刘勇,JEFFREY F.基于区间直觉模糊的动态多属性灰色关联决策方法[J].控制与决策,2013,28(9):63-68.

[4] 张小芝,朱传喜,朱丽.一种基于变权的动态多属性决策方法[J].控制与决策,2014,29(3):33-38.

[5] 苏志欣,王理,夏国平.区间数动态多属性决策的VIKOR扩展方法[J].控制与决策,2010,25(6):836-840.

[6] 赵妍,吴涛.论动态直觉模糊数的灰色关联多属性决策方法[J].合肥学院学报,2014,11(24):23-26.

[7] 周佳敏,王展青.基于三角模糊数的动态混合多属性决策法[J].武汉理工大学学报:信息与管理工程版,2014,2(6):28-32.

[8] 胡浩,徐少华.直觉模糊动态信息交互的多属性群决策模型[J].中南大学学报,2015,8(8):45-49.

[9] KRASSIMIR T.New operations defined over the intuitionistic fuzzy sets[J].Fuzzy sets and Systems,1994,61(1):137-142.

[10] BUSTINCE H,BURILLO P.Correlation of Interval-valued lntuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1995,74(2):237-244.

[11] CHEN S M,TAN J M.Handling multicriteria fuzzy decision-making problems based on Vague set theory[J].Fuzzy Sets and Systems,1994,67:163-172.

[12] HONG D H,CHOI C H.Multicriteria fuzzy decision-making problems based on vague set theory[J].Fuzzy Sets and Systems,2000,114:103-113.

[13] 刘华文.多目标模糊决策的Vague集方法[J].系统工程理论与实践,2004(5):103-109.

[14] XU Z S,YAGER R R.Dynamic lntuitionistic Fuzzy Multiple Attribute Decision Making[J].international Journal of Approximate Reasoning,2008,48(1):216-262.

Dynamic Intuitionistic Fuzzy Multiple Attribute Decision-making Method Based on Distance Model

MEIXiaoling

(Department of Maths and Finance, Yunyang Teachers’ College, Shiyan 442000,China)

For the dynamic multiple attribute decision-making problems that the time-weights of different period was known, and the attribute values was given in the form of intuitionistic fuzzy number, The comprehensive evaluation value was obtained. by using the DIFWA operator to integrate the evaluation value of each period, At the same time, a new scoring function of intuitionistic fuzzy sets was built, and the information of the intuitionistic fuzzy hesitation index was fully considered and digged to greatly improve the accuracy of evaluation of intuitionistic fuzzy number. The scoring function was used to determine positive and negative ideal point of the index set of intuitionistic fuzzy multiple attribute decision making. And the absolute excellent and inferior point should be avoided. The model of sorting based on distance formula was constructed, and the whole scheme set was sorted and picked over. Finally an example proved the practicability and feasibility of this method.

dynamic multiple attribute decision-making; intuitionistic fuzzy number; DIFWA operator; scoring function

2015-11-12

湖北省教育厅重点科研项目(D20155001; D20156001)；湖北省教育厅青年科研项目(Q20145001)

梅晓玲(1980-)，女，湖北十堰人，讲师，硕士，主要从事系统优化方面的研究，(E-mail) meixiaoling2005@126.com

1673-1549(2016)01-0096-05

10.11863/j.suse.2016.01.20

TB115

A