基于矩阵2-范数池化的卷积神经网络图像识别算法

余 萍， 赵继生

(华北电力大学电子与通信工程系，河北 保定 071003)

基于矩阵2-范数池化的卷积神经网络图像识别算法

余 萍， 赵继生

(华北电力大学电子与通信工程系，河北 保定 071003)

卷积神经网络中的池化操作可以实现图像变换的缩放不变性，并且对噪声和杂波有很好的鲁棒性。针对图像识别中池化操作提取局部特征时忽略了隐藏在图像中的能量信息的问题，根据图像的能量与矩阵的奇异值之间的关系，并且考虑到图像信息的主要能量集中于奇异值中数值较大的几个，提出一种矩阵2-范数池化方法。首先将前一卷积层特征图划分为若干个互不重叠的子块图像，然后分别计算子块图像矩阵的奇异值，将最大奇异值作为每个池化区域的统计结果。利用5种不同的池化方法在Cohn-Kanade、Caltech-101、MNIST和CIFAR-10数据集上进行了大量实验，实验结果表明，相比较于其他方法，该方法具有更好地识别效果和稳健性。

深度学习；卷积神经网络；矩阵2-范数；池化；奇异值

近年来兴起的卷积神经网络技术已经成为计算机科学领域的研究热点，其通过多个阶段的变换，深度挖掘隐含信息的本质特征，由于可以直接将原始图像作为网络的输入，避免了复杂特征

提取和数据重建，因此被广泛应用在文本、语音、图像识别等领域[1-5]。池化是卷积神经网络架构中的重要组成部分，其核心思想源于 Hubel和Wiesel[6]有关哺乳动物视觉皮层模型结构的开创性研究工作以及Koenderink和Van Doorn[7]提出的图像局部相关性原理，是将某些固定区域的联合分布统计结果作为特征检测器的响应，用于实现图像变换的缩放不变性，以使得网络对噪声和杂波有很好的鲁棒性。通过池化操作，可以减少数据处理量并保留有用信息[8-9]。池化操作在卷积神经网络结构中非常重要，可对网络性能产生很大的影响，因此研究行之有效的池化方法是必要的。

1982年，Fukushima和Miyake[10]在神经认知机中采取特征池化的方法用于图像识别，为其后计算机视觉识别模型中运用池化操作奠定了基础；Lecun等[11-12]使用均值池化的方法成功训练出第一个基于误差梯度的卷积神经网络；Ranzato等[13]、Jarrett等[14]使用最大池化方法在 Caltech-101、MNIST和NORB数据集上取得了当时最好的测试效果；Sermanet等[15]使用向量范数池化方法将SVHN数据集的正确识别率提升到94.85%；Zeiler 和 Fergus[16]将一种简单而有效的随机池化方法用于防止卷积神经网络训练过程中产生的过拟合，并且取得了很好的效果。

均值池化方法考虑了池化区域里的所有元素，当使用 f(x) = max(0,x)线性修正函数(rectified linear units, ReLUs)对神经元进行激励时，在均值计算过程中有很多零元素会削弱较大激活值的贡献，不能很好地反映池化区域的特征，同时将会对权值的调整产生很大影响；尤其是使用双曲正切函数(tanh)时，由于tanh函数关于零点反对称，正负激活部分可能会相互抵消，导致很微弱的池化反应。最大池化很好地解决了上述问题，但是由于其只选取了每个池化区域的最大值，使得较小的激活值无法向下一层传递信息，在实际应用中容易产生过拟合，网络的泛化能力较差，很难将其推广到测试集上。随机池化方法因为是根据多项式分布按照概率随机选取激活值，在采样层测试阶段采取概率加权池化的方法下，使用tanh函数作为激励时，由于负数的存在，使得测试阶段计算出来的加权激活值与训练阶段随机选取的激活值差别很大，测试分类效果很差[16]。向量范数池化方法在进行特征提取时，需要选取多种形式的向量范数池化方法进行比较才能选择出表现良好性能的策略，降低了算法性能，使其并没有得到大规模运用。本文提出一种基于矩阵 2-范数的池化方法，将矩阵的最大奇异值作为池化区域统计结果，在常用的Cohn-Kanade、Caltech-101、MNIST和CIFAR-10数据集上的测试结果表明，该池化方法相比较于其他方法具有更好的识别效果。

1 卷积神经网络

卷积神经网络是一个多层的非全连接的神经网络，融合局部感受野、权值共享和子采样这 3种结构特性使其自适应实现图像的旋转、平移和缩放等形式变换[12,17]。局部感受野是指每一层网络的神经元只与上一层某个固定大小的相邻矩形区域内的神经元相连接，通过局部感受野，神经元可以提取到方向线段、端点和角点等初级视觉特征。权值共享极大地减少了网络模型需要训练的参数个数，降低了模型复杂度。子采样降低了特征图的空间分辨率，提高了模型抗噪能力。图 1为本文所用到的一个 Cohn-Kanade实验的卷积神经网络模型结构，包括输入层、卷积层(由C标识)、采样层(由S标识)、全连接层(由F标识)和输出层。

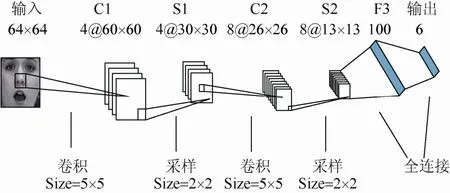
图1 Cohn-Kanade实验的卷积神经网络模型结构

1.1 卷积层

卷积层负责从输入图像的不同局部区域提取特征，可通过若干个可以学习的 × K K大小的卷积核与前一层的局部感受野进行卷积运算，并经过激活函数的非线性作用得以实现。每个卷积层由多个特征图组成，而每个特征图又可与前一层的多个特征图建立关系。卷积层的输入与输出形式分别为

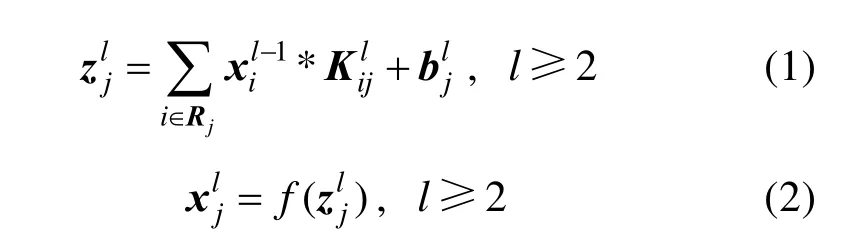
其中，Rj表示输入特征图的一个选择；是第(l- 1)层的第i个特征图的激活值；是第l层的第j个特征图与第( l-1)层的第i个特征图相连的卷积核；是第l层的第j个特征图的偏置；f(·)表示神经元的激活函数，常采用的有饱和非线性函数(例如：sigmoid，表达式为 f(x) = (1 + e-x)-1；tanh等函数)和不饱和非线性函数(例如：softplus，表达式为 f(x) = ln(1+ex)；ReLUs等函数)。

1.2 采样层

采样层是将卷积层的特征图进行抽样以提取用于分类的重要特征，即把输入的特征图划分为多个不重叠的子块，然后对每个子块进行池化操作。采样层只是做简单的缩放映射，采样层的特征图与前一层的特征图是一一对应的关系，假设前一个卷积层的特征图大小为N×N，第j个特征图矩阵记为，其中表示卷积层第j个特征图矩阵元素，s和t为对应的序号。采样窗口大小为n×n，采样层的输出为，其中。采样层主要有均值池化、最大池化、向量范数池化和随机池化4种构建方式，其计算公式如下：

(1) 均值池化的每个池化区域矩阵元素输出形式为

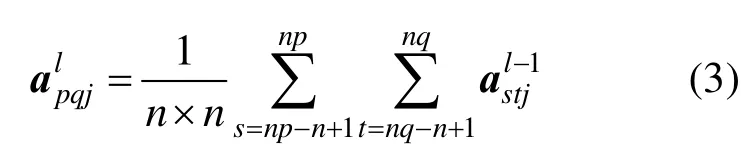
(2) 最大池化的每个池化区域矩阵元素输出形式为

(3) 向量范数池化的每个池化区域矩阵元素输出形式为

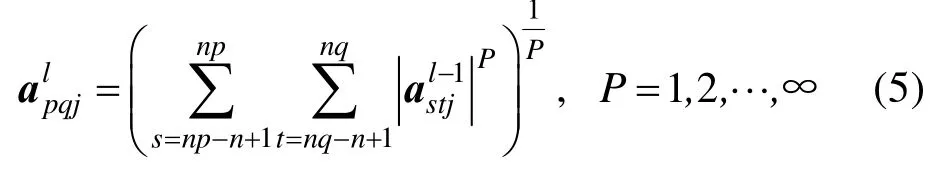
其中，P的取值不同代表了不同形式的向量范数。

(4) 随机池化的每个池化区域矩阵元素输出形式为

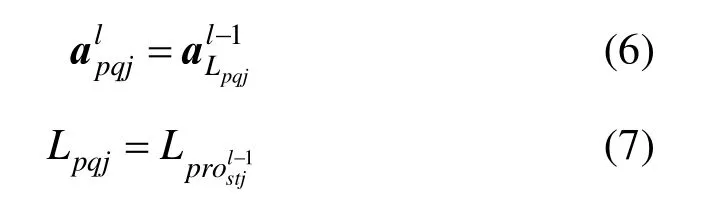
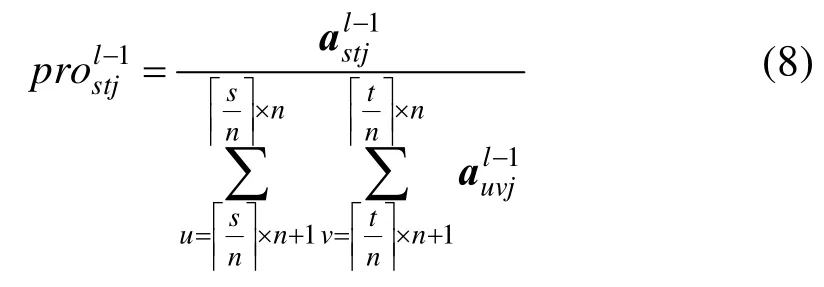
其中，“⌈⌉”为向上取整符号。

卷积神经网络通过卷积层和采样层的交替作用来学习原始图像的隐含特征，一般再经过若干个普通神经网络里的全连接层，其输入和输出形式为

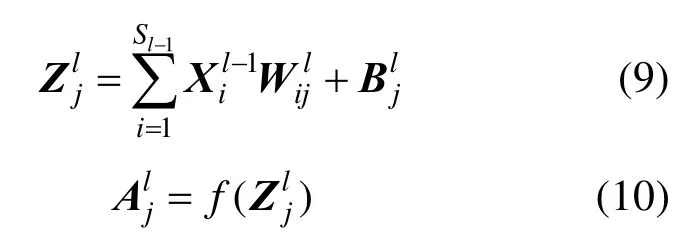
按照梯度下降的原则，基于反向传播算法(back propagation, BP)来调整相应的权重和偏置值。其中，全连接层权重值的更新公式为[18]

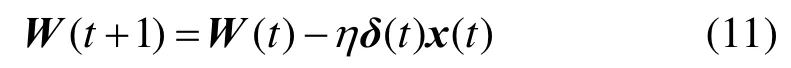
其中， x (t )表示该神经元的输出； δ (t)表示该神经元的残差项；η表示学习率。

2 基于矩阵2-范数的池化方法

(3) 三角不等式：对于 ∀B∈Rn×n，有；

(4) 相 容 性 ： 对 于 ∀B∈Rn×n， 有

根据以上矩阵范数的定义，介绍 2种常见的矩阵范数：

① Frobenius范数(F-范数，是向量 2-范数的推广)

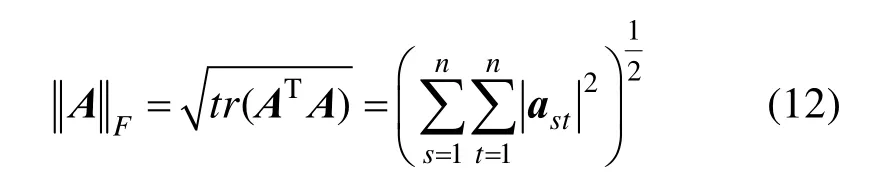
② 谱范数(矩阵2-范数)

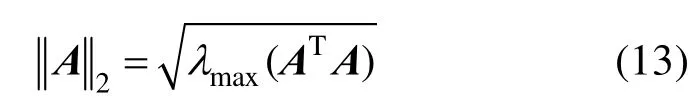
其中， AT为A的转置矩阵， λmax(ATA)为ATA的最大特征值。

对方阵A进行奇异值分解有 A =UDVT，其中U和V都是正交矩阵， D=diag(d1,d2,···,dr)为对角矩阵，并且满足d1≥ d2≥··· ≥ dr＞0是矩阵A 的r个奇异值，r为矩阵A的秩。矩阵A的 F-范数和2-范数又可以表示为

由式(14)、(15)可知，图像的能量信息可以用矩阵的奇异值来表征，当图像发生旋转、平移、缩放等几何失真时，根据奇异值分解理论，图像矩阵的奇异值只发生很微小的变化，即图像的能量信息具有较高的稳定性[19-21]。因此，可将图像的能量作为向下一层网络传递的信息，以使得图像的几何失真具有高度不变性。考虑到图像信息的主要能量集中于奇异值中数值较大的几个，本文提出一种基于矩阵2-范数的池化方法，将矩阵的最大奇异值作为池化区域统计结果。相比较于F-范数方法，不仅计算简单，且具有更好的稳健性。

以图 2所示的一个池化过程为例，描述本文提出的矩阵2-范数的池化方法：

步骤 1. 将N×N大小的卷积层特征图划分为若干个互不重叠的子块矩阵，每个子块矩阵的大小为n×n(图2的卷积层特征图中数字区域为其中一个子块矩阵)；

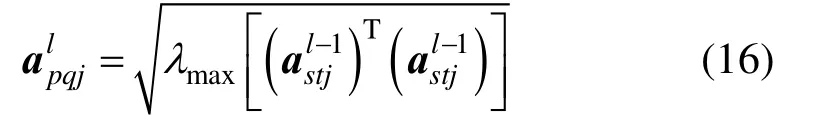
涉及到反向传播过程中，由式(11)可知，主要是计算残差项 δ( t)。

(1) 当l层是卷积神经网络中的输出层时，第i个神经元节点的残差为

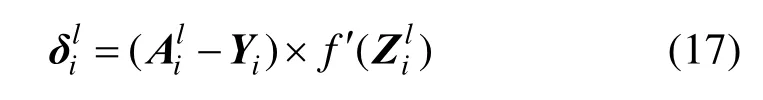
其中，Yi表示理想状态下的第i维标签，为非线性映射函数的导数，由于输出层用于分类使用的是sigmoid函数，因此，式(17)可以记为

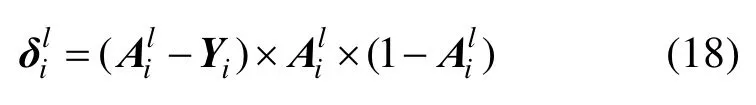
(2) 当l层是全连接层时，第i个神经元节点的残差为

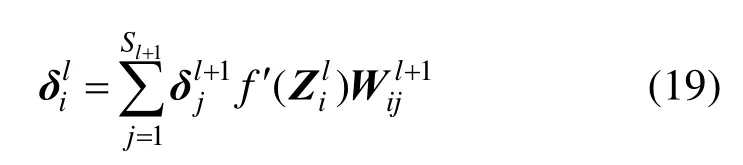
(3) 虽然采样层没有训练的参数，不需要进行参数更新，但是后面与之连接的卷积层和全连接层在计算残差项时需要对其进行相应的操作。因此，仍然需要计算采样层的残差。

①当采样层的下一层是卷积层时，第i个特征图的残差为

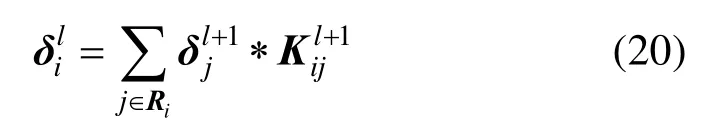
②当采样层的下一层是全连接层时，需要将最后一个采样层的二维特征图拉伸为特征列向量，这里计算的是特征向量中第 i个神经元节点的残差

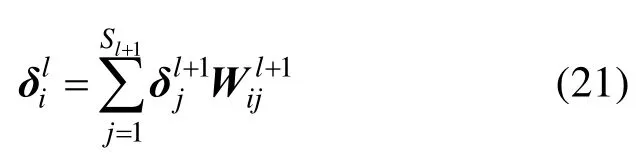
(4) 当l层是卷积层时，需要将图2采样层中的一个元素对应的残差项进行上采样，本文的策略类似于均值采样，将一个元素对应的残差上采样成具有相同元素的n×n大小的矩阵，第i个特征图的残差为

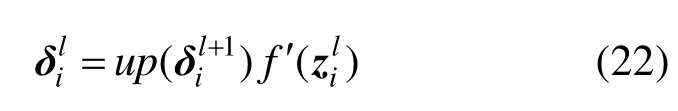
其中， up(·)为一个上采样函数，就是计算下一个采样层的残差与一个n×n大小的全 1矩阵的克罗内克积。

图2 矩阵2-范数的池化过程举例

3 实验及结果分析

为了验证矩阵 2-范数池化方法的有效性，并且考虑到矩阵 2-范数的定义条件，本文探讨在不同池化方法下，卷积层采取目前广泛使用的ReLUs函数，而全连接层使用sigmoid函数作为激活函数的图像识别效果。实验在 Matlab2013a环境下完成，采用的操作系统为Windows 8.1，CPU为Intel i5-4210m，主频为2.6 GHz，内存为8 G。实验中的训练次数最大设置为50次。

3.1 Cohn-Kanade数据集实验结果

Cohn-Kanade(CK)数据集是美国卡内基梅隆大学机器人研究所和心理学系共同建立的人脸表情库，本文首先将 CK数据库中的图片裁剪成64×64大小的表情图片，分为愤怒、厌恶、高兴、恐惧、惊讶和悲伤等6种不同的表情，包含1 839张图像，图3为Cohn-Kanade实验中用到的部分图像。实验中，每种表情都是随机选取大约 90%的图片作为训练样本，其余的作为测试样本。

图3 Cohn-Kanade实验中用到的部分图像

在图1所示的Cohn-Kanade实验的卷积神经网络模型结构中，第一个卷积层C1通过5×5大小的卷积核获得 4个 60×60大小的特征图，共有4×(5×5+1)=104个需要训练的未知参数；接下来的采样层S1对C1中所有互不重叠的2×2大小的子块进行池化操作，得到4个30×30大小的特征图，不含有未知参数；余下的C2和S2层与此相类似；F3是一个与 S2全连接的网络层，神经元个数为100，总共有100×8×(13×13)+100=135300个连接；输出层包含6个节点，使用全连接层的100维向量进行分类。图4显示了一张输入图像在矩阵2-范数池化网络模型的卷积层和采样层中的特征图，各特征的数值分布于0到1之间，黑色为0，白色为 1。在采样层使用不同池化方法下，Cohn-Kanade数据集的分类正确率如表1所示。从表1可看出，对于愤怒表情，最大和向量2-范数池化均能正确识别，而矩阵2-范数池化有1张错误识别；对于厌恶和高兴表情，只有均值和随机池化方法有 1张错误识别，其他池化方法均能正确识别；对于恐惧表情，5种池化方法都能正确识别；对于惊讶和悲伤表情，只有矩阵 2-范数池化方法识别效率好。矩阵2-范数池化方法在CK数据集上的正确识别率为97.77%。

图4 矩阵2-范数池化网络模型的卷积层和采样层中的特征图

表1 Cohn-Kanade数据集在不同池化方法下的分类正确率

3.2 Caltech-101数据集实验结果

Caltech-101数据集包含101类物体和一类背景图像，总共有9 144张大约300×300分辨率的图像，每类的图片数目从31到800张不等。考虑到特征维数较高会带来内存溢出问题，本文选取类别图像中数目大于 400张的作为实验对象，包括background、faces、faces_easy、motorbikes和airplanes 5类共计2 935张图像，每类随机选取M张图像做训练，训练样本共 5×M 张，其余的2935–5×M张为测试样本。为了满足输入图片的要求，使用双线性插值算法将其归一化为 140×140的灰度图像，图5为Caltech-101实验中用到的部分图像。

图5 Caltech-101实验中用到的部分图像

本研究设计的Caltech-101实验的卷积神经网络结构如图6所示的2个卷积层、2个采样层和1个全连接层，第一个卷积层的特征图个数为9，卷积核的大小为16×16；第二个卷积层的特征图个数为 18，卷积核的大小为 6×6；采样窗口大小都为5×5；全连接层的神经元个数为200。

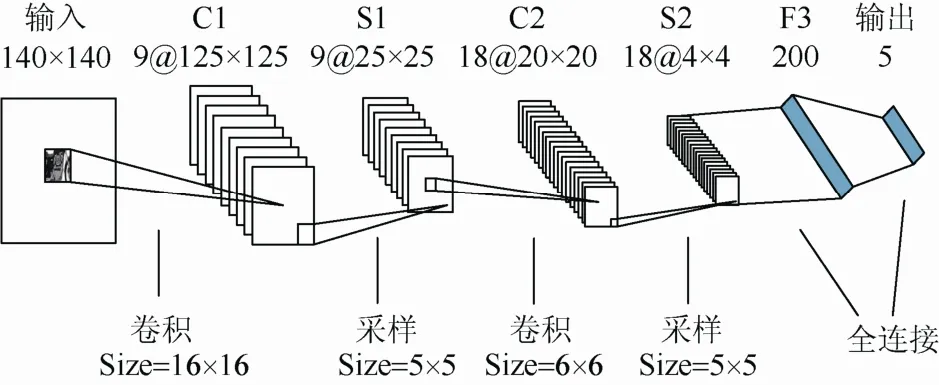
图6 Caltech-101实验的卷积神经网络模型结构

采样层使用不同池化方法，在训练样本不同时分类正确率如表2所示。从表2可以看出，本文提出的矩阵 2-范数池化方法比其他池化方法具有较高的识别率，而且训练样本的个数直接影响到识别率。当每类训练样本个数为 300时，本文提出的池化方法在测试样本集上的识别率为93.24%。

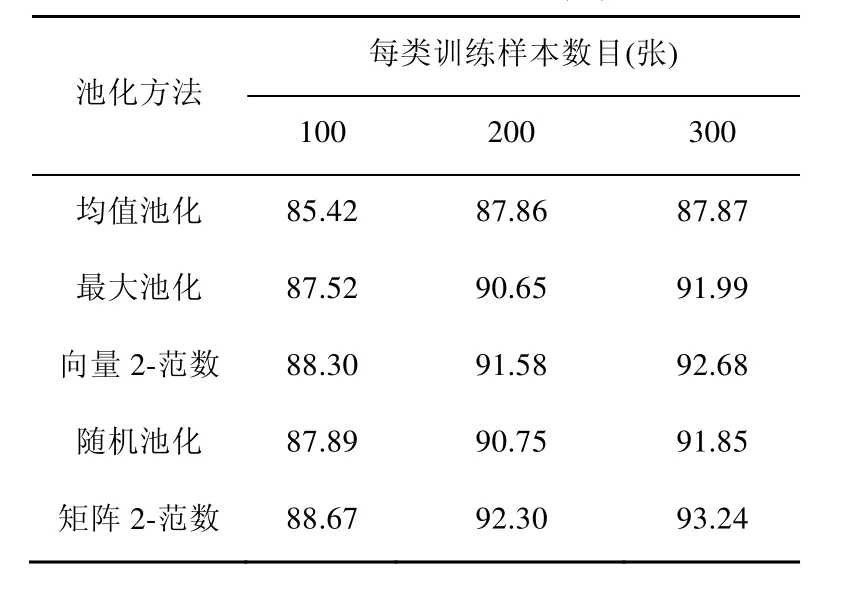
表2 Caltech-101数据集中训练样本不同时，不同池化方法下的网络分类正确率(%)

3.3 MNIST数据集实验结果

MNIST手写字体(0~9数字)数据集共计60 000张训练图片和10 000张测试图片，每张图片均为28×28的灰度图像，实验中只需要将其归一化为[0，1]。采用经典的卷积神经网络结构包括2个卷积层、2个采样层和1个全连接层，卷积核的大小为5×5，采样窗口大小都为2×2；第一个卷积层的特征图个数为 6，第二个卷积层的特征图个数为12，全连接层的神经元个数为200。在采样层采取不同池化方法下，网络分类正确率随着训练次数变化曲线如图7所示。

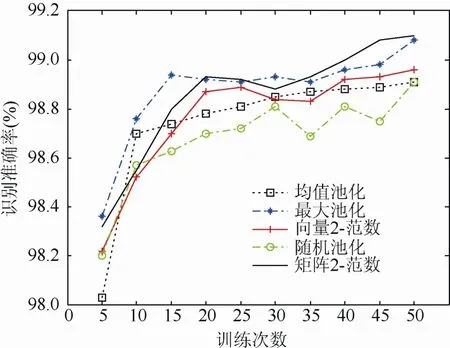
图7 MNIST数据集中不同池化方法的网络分类正确率随着训练次数变化曲线

MNIST数据集中的数字特征比较简单，从图7可以看出，5种池化方法都取得了不错的识别效果，在训练35次之后，使用矩阵2-范数池化方法的网络分类正确率要高于其他方法。表 3的结果为 5种池化方法的最好识别结果，本文提出的方法在经典卷积神经网络结构下的正确率最高为99.10%。

表3 MNIST数据集在不同池化方法下的网络分类正确率(%)

3.4 CIFAR-10数据集实验结果

CIFAR-10数据集包含10类50 000张训练图片和10 000张测试图片，每张图片均为32×32的彩色自然图像，实验中先将图像转换成灰度，再进行均值和方差归一化，最后进行ZCA白化操作。采用的网络结构设置为：8C1-4S1-16C2-4S2-240F3，卷积核大小为5×5。网络结构设置中的 C表示卷积层，前面对应的数字表示相应层的特征映射图个数；S表示采样层，前面对应的数字表示采样窗口的大小；F表示全连接层，对应的数字表示神经元的个数。在采样层使用不同池化方法下，CIFAR-10数据集的分类错误率如表4所示。从CIFAR-10数据集实验结果可以看出，使用矩阵2-范数池化方法提高了识别准确率。

表4 CIFAR-10数据集在不同池化方法下的网络分类错误率(%)

以上的实验结果说明，MNIST样本空间变化比较小，5种池化方法的识别率相差不大，但是使用矩阵 2-范数池化方法的识别率还是最高的，而在Cohn-Kanade、Caltech-101和CIFAR-10数据集上，识别率提升效果比较明显，体现了本文方法在复杂特征样本上具有较大的优势。进一步说明，采样层使用矩阵 2-范数池化方法在降低特征图分辨率的同时，保留了主要能量信息。

4 结束语

本文根据矩阵的奇异值分解对于图像的几何失真具有高度不变性的原理，考虑到图像信息的主要能量集中于奇异值中较大的几个，提出一种基于矩阵 2-范数的卷积神经网络池化方法，首先将卷积层特征图划分为若干个互不重叠的子块图像，然后分别计算子块图像矩阵的奇异值，将矩阵的最大奇异值作为池化区域统计结果。该方法将图像的能量信息作为下一层网络传播的特征，同时也不至于使得信息特征过于复杂化。在Cohn-Kanade、Caltech-101、MNIST和CIFAR-10公开数据集上的对比测试表明：本文方法具有更高的识别率和很好的稳健性，可以反映隐含在图像中的能量信息特征。

[1] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks [J]. Advance in Neural Information Processing Systems, 2012, 25(2): 1097-1105.

[2] Ji S W, Xu W, Yang M, et al. 3D convolutional neural networks for human action recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 221-231.

[3] Dahl G E, Sainath T N, Hinton G E. Improving deep neural networks for LVCSR using rectified linear units and dropout [C]//Acoustics, Speech and Signal Processing (ICASSP). New York: IEEE Press, 2013: 8609-8613.

[4] Jin J Q, Fu K, Zhang C S. Traffic sign recognition with hinge loss trained convolutional neural networks [J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 1991-2000.

[5] Kim I J, Xie X H. Handwritten Hangul recognition using deep convolutional neural networks [J]. International Journal on Document Analysis and Recognition, 2014, 18(1): 1-13.

[6] Hubel D H, Wiesel T N. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex [J]. The Journal of Physiology, 1962, 160(1): 106-154.

[7] Koenderink J, Van Doorn A. The structure of locally orderless images [J]. International Journal of Computer Vision, 1999, 31(2/3): 159-168.

[8] Boureau Y L, Ponce J, Lecun Y. A theoretical analysis of feature pooling in visual recognition [C]//Proceeding of the 27th International Conference on Machine Learning. Haifa, Israel: ICML, 2010: 111-118.

[9] Scherer D, Müller A, Behnke S. Evaluation of pooling operations in convolutional architectures for object recognition [C]//20th International Conference on Artificial Neural Networks. Berlin: Springer, 2010: 92-101.

[10] Fukushima K, Miyake S. Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position [J]. Pattern Recognition, 1982, 15(6): 455-469.

[11] Lecun Y, Boser B, Denker J S, et al. Handwritten digit recognition with a back-propagation network [C]// Advances in Neural Information Processing Systems. San Francisco, CA: Morgan Kaufmann Publishers, 1990: 396-404.

[12] Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition [J]. Proceeding of the IEEE, 1998, 86(11): 2278-2324.

[13] Ranzato M, Boureau Y L, Lecun Y. Sparse feature learning for deep belief networks [C]//Neural Information Processing Systerms. Cambridge: MIT Press, 2007: 1185-1192.

[14] Jarrett K, Kavukcuoglu K, Ranzato M, et al. What is the best multi-stage architecture for object recognition [C]// 2009 IEEE 12th International Conference on Computer Vision. New York: IEEE Press, 2009: 2146-2153.

[15] Sermanet P, Chintala S, Lecun Y. Convolutional neural networks applied to house numbers digit classification [C]// 21st International Conference on Pattern Recognition. New York: IEEE Press, 2012: 11-15.

[16] Zeiler M D, Fergus R. Stochastic pooling for regularization of deep convolutional neural networks [C]// International Conference on Learning Representations. Arizona, USA: ICLR, 2013: 1-9.

[17] Lecun Y, Kavukcuiglu K, Farabet C. Convolution networks and applications in vision [C]//Proceedings of 2010 IEEE International Symposium on Circuits and Systems. New York: IEEE Press, 2010: 253-256.

[18] Hinton G E. How neural networks learn from experience [J]. Scientific American, 1992, 267(3): 145-151.

[19] Wall M E, Rechtsteiner A, Rocha L M. Singular value decomposition and principle component analysis [J]. A Practical Approach to Microarray Data Analysis, 2002, 5: 91-109.

[20] 周 波, 陈 健. 基于奇异值分解的、抗几何失真的数字水印算法[J]. 中国图象图形学报, 2004, 9(4): 506-512.

[21] 朱晓临, 李雪艳, 邢燕, 等. 基于小波和奇异值分解的图像边缘检测[J]. 图学学报, 2014, 35(4): 563-570.

Image Recognition Algorithm of Convolutional Neural Networks Based on Matrix 2-Norm Pooling

Yu Ping, Zhao Jisheng

(Department of Electronics and Communication Engineering, North China Electric Power University, Baoding Hebei 071003, China)

The pooling operation in convolutional neural networks can achieve the scale invariance of image transformations, and has better robustness to noise and clutter. In view of the problem that pooling operation ignores the energy information hidden in the image when it extracts local features for image recognition, according to the relationship between energy of the image and singular value of the matrix, and taking into account the image information of the energy mainly concentrates on the larger singular value, a pooling method based on matrix 2-norm was proposed. The former feature map of convolutional layer is divided into several non-overlapping sub blocks, and then singular value of the matrix is calculated. The maximum value is used as the statistical results of each pooling region. Various numerical experiments has been carried out based on Cohn-Kanade, Caltech-101, MNIST and CIFAR-10 database using different kinds of pooling method. Experimental results show that the proposed method is superior in both recognition rate and robustness compared with other methods.

deep learning; convolutional neural networks; matrix 2-norm; pooling; singular value

TP 391

10.11996/JG.j.2095-302X.2016050694

A

2095-302X(2016)05-0694-08

2015-07-20；定稿日期：2016-04-25

余 萍(1963–)，女，浙江富阳人，副教授，学士。主要研究方向为图像处理、模式识别。E-mail：well_yp@yeah.net