“轻负”源自“高效”

唐乾青

摘 要：轻负高效其目的就是要减轻学生负担，提高教学质量，那如何实现“轻负”、“轻负到底源自哪里”是值得教师深思的问题，结合自身教学经验，在新课程视野下，从“高效备课、高效课堂、高效总结、高效作业”等几个方面浅谈初三数学复习课的高效性。

关键词：轻负；高效备课；高效课堂；高效总结；高效作业；初三复习课

如何优化中考复习模式，追求复习效益最大化是我们初三老师孜孜追求的目标。中考复习的目的是帮助学生对已学过的零碎的数学知识进行归类、整理、加工，使之规律化、网络化，从而使学生掌握的知识更为扎实，更为系统，能更好地提高学生分析问题、解决问题的能力。如何真正做到轻负担，高效率，我认为要把工夫花在每节课上，只有提升了每节课的教学水平，才能真正地做到轻负高效，所以，我坚持上课质量第一的原则，把功夫下在课前，效率体现在课中，素质展现在课后。

一、轻负源自高效备课

俗话说：“台上一分钟，台下十年功。”作为一名老师，要想上好一节课，就必须充分备课。在复习完二次函数相关的基础内容之后，在相应的提升练习当中经常会碰到点的存在性问题，于是我想能否将这些题“化零为整”呢？以一道题为模板，将点的存在性问题的各种情况全部归纳进去，学生真正明白了，还会犯愁吗？于是我对湖北潜江的一道中考试题进行了改编：

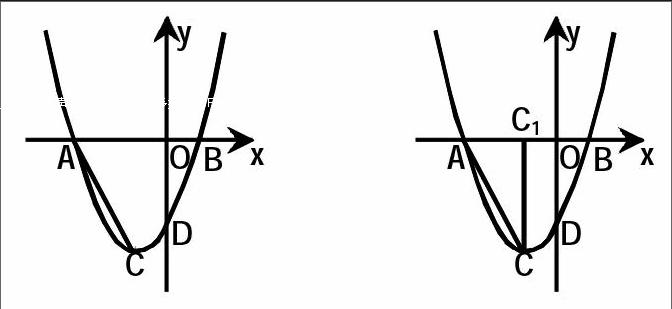
在平面直角坐标系中，抛物线y=ax2+bx-3与x轴的两个交点分别为A（-3，0）、B（1，0），且交y轴于点D，顶点为C，连结AC。

（1）直接填写：a= ，b= ，顶点C的坐标为 。

（2）已知R（-2，-3）是抛物线上的一点，则在抛物线上是否存在另一点H，使得S△ABH=S△ABR，若存在，请直接写出点H坐标，若不存在，说明理由。

（3）在x轴上是否存在点E，使得△ACE是等腰三角形？若存在，求出点E的坐标；若不存在，说明理由；

（4）在y轴上是否存在点F，使得△ACF为直角三角形？若存在，求出点F的坐标；若不存在，说明理由；

（5）点M（-0.5，b）在抛物线上，点N为抛物线上一动点，在x轴上是否存在点P，使以A、M、N、P为顶点的四边形是平行四边形，如果存在，求出所有满足条件的点P的坐标，若不存在，请说明理由。

（6）在此抛物线上是否存在点Q，使得以A、C、D、Q四点为顶点的四边形是梯形？若存在，求出点Q的坐标，若不存在，请说明理由。

（7）过点C作CC1⊥AB于点C1，若点P1为x轴下方的抛物线上一动点（点P1与顶点C不重合），P1Q1⊥AC于点Q1，当△P1CQ1与△ACC1相似时，求点P1的坐标。

存在性问题是探索型问题中的一种典型性问题，这类考题是近年来全国各地中考的热点问题，其特点是在一定条件下探索发现某些数学结论或规律是否存在的问题，纵观中考的压轴题，有关点的存在性问题，无非就是找第三（或第四）个点，使得某三角形（或四边形）为等腰三角形或直角三角形（或平行四边形、梯形等），于其零零散散地讲，不如将其综合到一起，讲个痛快，讲个明白，让学生也清清楚楚。

二、轻负源自高效课堂

高效课堂的主要特征为主动性、生动性、生成性。主动是学习状态，“主动”会激发潜能、乐在其中，带来效益、生成能力；生动性，是追求课堂的情感价值，突出“学乐”和“乐学”，学习如饮甘露琼浆，变“怕上学”为“怕下课”；生成性，课堂要敢于变各种“句号”“叹号”为“问号”。追求“主体多元”，鼓励不同个性的学习见解，让思维激荡思维，让思想冲撞思想，让方法启迪方法。课堂的智慧、高潮、价值尽在“不可预设”的“现场生成”上，一切的预设应服务于“现场”，而不是让“现场”服务于预设。

给学生点时间，他们很快搞定了预设的（1）（2）（3）三题，对于（4），先由学生独立思考，然后再小组讨论，此处直角顶点没有确定，同样要分三种情况解决，对于以点A或点C为直角顶点时，只要过点A（或C）作AC的垂线交y轴于点F，借助于三角函数或解析式法不难求出点F的坐标；但当以点F为直角顶点时，学生的方法有很多，不同层次的学生都举起了手，于是我索性让他们探究个够。

生1：设点F的坐标为（0，y）可根据勾股定理得AF2+CF2=AC2解出即可。

生2：可用相似，设点F的坐标为（0，y），过点C作CG⊥OD于点G，证明△AOF∽△FGC即可。

生3：直接借助于三角函数（当然这是在两三角形相似的前提下）

生4：只要以AC为直径画圆交y轴于点F，接下来求点F坐标方法颇多……

学生在这种乐学、好学的氛围中完成着后面几题。这样的课堂真正由“一言堂”变成“群言堂”，每个学生都成为课堂的主人，效率还会差吗？我觉得初三复习课重要的是要扣联系点，拓展外延，深化内涵，总结升华，整合知识，以提高解题能力。

三、轻负源自高效总结

叶澜教授说过，一个教师写一辈子教案也成不了名师，写三年教学反思就可能成为名师。同样道理，一个学生能够养成质疑、反思的习惯，就具备了良好的数学素养。题海无涯，总结是岸！对于上面题目，每分析一题，我就引导学生进行总结，主要是解题方法的理解掌握， 数学思想方法的渗透归纳；总结解析这类题目的通则，留给学生足够时间去体会、感悟，触类旁通，逐渐养成善于总结创新、勤于思考的数学思维品质。平时我们也这么要求学生了，还担心他们的成绩吗？常总结，促高效！

四、轻负源自高效作业

初三学生在复习时间上安排得很紧张，如何让他们有效地去做而不是疲惫应付呢？在平时教学中我尽力要求自己没有做过的题，不给学生做。我要像学生一样，逐题解答资料上的习题，从读题，到审题、规范解答，筛选出“好题”来。所谓好题，就是基础题、高频题，就是紧扣考点，不偏不怪、难易适宜，知识与能力结合完美、目标指向明确的题目。这样的题目有代表性，价值大，做会了、弄明白了，可以以一当十，作业自然达到了高效！

古希腊普鲁塔戈曾指出：“头脑不是一个要被填满的容器，而是一把需要被点燃的火把。”作为一名初三老师，应坚持“把功夫下在课前，效率体现在课中，素质展现在课后”的原则，充分调动学生上课的积极性，集中相关知识点提高课堂复习效率，精选题目，让师生真正体会到“轻负”源自“高效”！

参考文献：

[1]孙强.论人的全面发展思想对教育创新的启示[J].扬州大学，2008.

[2]刘艳，钮丽丽，邹泓.对中学生压力状况的研究[A].第九届全国心理学学术会议文摘选集[C]，2011.

[3]刘燕青.从知识传授能力培养到人的全面发展：人类教育观念变革初探[J].中央音乐学院党校，2009（3）.

[4]孙启胜.数学教学要注意培养学生的现代意识[J].山东教育，1997（24）.

[5]郑小兵.浅谈数学课堂教学的有效性[J].中学数学研究 2012（1）.

[6]潘翠霞.课堂教学中充分发挥学生的主体性[J].中学数学研究，2012（1）.