传统三段论的形式化和公理化研究
张晓君,李晟
(四川师范大学逻辑与信息研究所,四川成都610068)
传统三段论的形式化和公理化研究
张晓君,李晟
(四川师范大学逻辑与信息研究所,四川成都610068)
利用广义量词理论对四个亚里斯多德量词的真值定义,可以对传统三段论进行形式化。在AAA-1和EAE-1这两个公理的基础上,利用四个亚里斯多德量词的单调性之间的可转换关系,可以对传统三段论进行公理化。这些创新性成果,对于自然语言信息处理以及计算机科学中的知识表示和知识推理,都有着重要的理论意义和实践价值。
广义量词理论;传统三段论;亚里斯多德量词;形式化;公理化
一、引言
亚里斯多德学派认为,根据第一格AAA式(简记为AAA-1)三段论和第一格EAE式(简记为EAE-1,其他类似)三段论的有效性,可以推出除了预设主项存在的三段论以外的其他所有的有效的传统三段论[1]228。为此,他们主要利用换位法、归谬法和显示法等方法对其进行了非形式化的论证[2]94。“在我国语言学界和计算语言学界,缺乏语义分析的形式化成为中文信息处理的瓶颈问题”[3]。那么,我们是否可以对亚里斯多德学派的这一结论进行形式化的证实或证伪呢?如若能够证实的话,那么,这一创新性成果将为传统三段论建立起一个形式化和公理化的推理系统。由于绝大部分的自然语言推理(包括汉语推理)都可以用传统三段论或广义三段论(也叫扩展三段论)来加以形式化,并判断其是否有效[4]155~202,在对量化表达式的语义进行准确分析的基础上,对自然语言语句传达的信息进行准确的形式化刻画,是自然语言走向人工智能的第一步[5],因此,对传统三段论进行形式化和公理化,是一项十分有趣而且富有意义的工作,其研究成果将有利于自然语言处理(包括中文信息处理),以及计算机科学中的知识表示和知识推理。
本文的中心目的就是:在对传统三段论进行形式化的基础上,对传统三段论进行公理化。其研究思路和研究方法再一次证实了:(1)逻辑学研究重心已经转向多学科交叉融合的互动研究[6];(2)逻辑学的形式化研究存在多元化进路[7];(3)为了适应信息时代和人工智能时代的到来,现代逻辑正在对大范围的信息进行形式化的转换[8]。
《基于广义量词理论的亚氏三段论》一文,从广义量词理论(generalized quantifiers theory)的视角证明了:不同传统三段论之间的可化归性,本质上反映了all、some、no和not all这四个亚里斯多德量词(简称亚氏量词)与其三种否定量词的单调性、对称性等语义性质之间的关系的可转换性[4]176~177。由于三段论AAA-1的有效性表征了all的右单调递增性,而三段论EAE-1的有效性表征了no的左单调递减性,而且从一个亚氏量词的单调性和对称性,就可推出其三种否定量词的单调性和对称性[9],可见,要对传统三段论进行形式化和公理化,还需要从广义量词理论谈起。
二、相关基础知识
20世纪50年代以来,为了解释传统三段论形式以外的大量的有效推理,拓展一阶逻辑的表达力,提升计算机处理自然语言的能力,逻辑学家开始对一阶逻辑中量词加以扩展,引入了广义量词[10]482~525。广义量词包括:(1)一阶逻辑的全称量词∀和存在量词∃;(2)限定词;(3)由限定词a、an、the或其他量化关系指称所组成的所有名词短语[11]。比如“正好三个苹果”、“他的手机”、“所有的树木”、“没有”、“两者都不”、“几个”、“两打的”、“超过三分之二的”、“大多数的”、“不到一半的”等等都是广义量词。严格地说,对自然语言中的名词短语或限定词进行语义解释后,才能够得到集合论中的广义量词,即:名词短语或限定词的指称对应于广义量词[12]25。
广义量词理论的代表作主要有:Barwise和Cooper(1981)[13]、Keenan(1997)[14]、Peters和Westerståhl(2006)[15]、Szymanik(2009)[16]、Moss(2010)[17]和Chow Ka Fat(2012)[18]等。此理论的基本思想就是:利用广义量词的真值定义,来揭示广义量词所涉及的论元集合的性质或不同论元集合之间的关系,从而彰显自然语言中的广义量词的普遍语义性质及其推理特征[4]28。在本文中,Q表示广义量词,S、M、P表示论元的集合,E表示论域,符号“⇒”表示“蕴涵”。
广义量词可分为:〈1〉类型量词、〈1,1〉类型量词、〈1,1,1〉类型量词、〈1,2〉类型量词等等,前两种类型的量词是自然语言中最常见的[4]43。常见名词短语一般对应于〈1〉类型量词,大多数限定词一般对应于〈1,1〉类型量词[15]11~12。亚氏量词就是〈1,1〉类型的广义量词,它揭示了表示广义量词的左论元与右论元所涉及集合之间的二元关系[19]。以〈1,1〉类型量词开头的语句都具有QE(S,P)这样的三分结构,这种结构在自然语言中普遍存在。例如:“所有男孩子都贪玩”和“没有男孩子贪玩”,可以分别表示成allE(S,P)和noE(S,P)这样的三分结构。其中,all和no分别表示亚氏量词“所有”和“没有”,S表示论域E中男孩子组成的集合,P表示论域E中贪玩的个体组成的集合。在广义量词理论中,all和no的真值定义分别为:allE(S,P⇔S⊆P⊆E和noE(S,P)⇔S∩P=Ø,前者表示集合S包含于集合P,而后者表示集合S和集合P的交集为空集。
一个广义量词Q有三种否定形式[4]54~57,即,外否定(outer negation)┓Q、内否定(inner negation)Q┓、对偶(dual)否定Qd,其定义如下:
定义1〈1,1〉类型量词的三种否定运算
令E是任意的论域,且S,P⊆E,对〈1,1〉类型量词Q而言:
(1)(┓Q)E(S,P)⇔not QE(S,P);
(2)(Q┓)E(S,P)⇔QE(S,E-P);
(3)(Qd)E(S,P)⇔┓(Q┓)E(S,P)⇔(┓Q)E┓(S,P)。
对于四个亚氏量词而言,all与not all是互为外否定,no与some也是互为外否定;no与all是互为内否定,some与not all也是互为内否定;some与all是互为对偶否定,no与not all也是互为对偶否定。
广义量词的主要性质有:同构闭包性、扩展性、单调性、驻留性、相交性、对称性以及逻辑性[15]。单调性是广义量词最为重要的语义性质和推理性质。本文将用到的单调性和对称性定义如下:
定义2令QE是任意的〈1,1〉类型量词,E是任意的论域,且M,S,P⊆E
(1)QE是右单调递增的(简记为Mon↑),当且仅当:若P⊆M⊆E,则QE(S,P)⇒QE(S,M);
(2)QE是右单调递减的(简记为Mon↓),当且仅当:若P⊆M⊆E,则QE(S,M)⇒QE(S,P);
(3)QE是左单调递增的(简记为↑Mon),当且仅当:若S⊆M⊆E,则QE(S,P)⇒QE(M,P);
(4)QE是左单调递减的(简记为↓Mon),当且仅当:若S⊆M⊆E,则QE(M,P)⇒QE(S,P)。
定义3一个〈1,1〉类型的广义量词Q是对称的[15]206~214,当且仅当,对所有的论域E和所有的S,P⊆E而言,QE(S,P)⇒QE(P,S)。
广义量词的单调性与它的三种否定量词┓Q、Q┓和Qd的不同单调性之间,有着可以相互转换的关系,具体的转换关系可参见下面的单调性关系定理1,定理1的部分证明可以参见Peters and Westerståhl[15]170~171。
单调性关系定理1[20]对于一个〈1,1〉类型量词Q而言:
(1)Q是Mon↑,当且仅当,┓Q是Mon↓;(2)Q是Mon↑,当且仅当,Q┓是Mon↓;
(3)Q是Mon↑,当且仅当,Qd是Mon↑;(4)Q是Mon↓,当且仅当,┓Q是Mon↑;
(5)Q是Mon↓,当且仅当,Q┓是Mon↑;(6)Q是Mon↓,当且仅当,Qd是Mon↓;
(7)Q是↑Mon,当且仅当,┓Q是↓Mon;(8)Q是↑Mon,当且仅当,Q┓是↑Mon;
(9)Q是↑Mon,当且仅当,Qd是↓Mon;(10)Q是↓Mon,当且仅当,┓Q是↑Mon;
(11)Q是↓Mon,当且仅当,Q┓是↓Mon;(12)Q是↓Mon,当且仅当,Qd是↑Mon。
具体地说,四个亚氏量词的单调性及其相互关系如图1[20]。
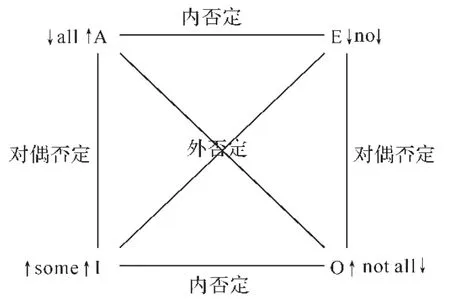
(图1)四个亚氏量词的单调性及其相互关系
即:对互为外否定的两个〈1,1〉类型的广义量词而言,其左右单调性相反;对于互为内否定的两个〈1,1〉类型的广义量词而言,其左单调性相同,右单调性相反;对于互为对偶否定的两个〈1,1〉类型的广义量词而言,其左单调性相反,右单调性相同[20]。由于亚氏量词是广义量词的特例,因此,这一结论也适合于四个亚氏量词。
三、传统三段论的形式化
要对传统三段论进行公理化的前提是先对其进行形式化。在下文中,S、P和M分别表示满足直言命题的主项、谓项、中项所表示性质的个体所形成的集合,E表示为所涉及的论域。因此,对于传统三段论所研究的A、E、I、O四个直言命题而言:
(1)A命题,即:全称肯定命题“所有S是P”,可以表示成allE(S,P)这样的三分结构。
(2)E命题,即:全称否定命题“所有S不是P”,意思是“没有S是P”,可以表示成noE(S,P)这样的三分结构。
(3)I命题,即:特称肯定命题“有S是P”,可以表示成someE(S,P)这样的三分结构。
(4)O命题,即:特称否定命题“有S不是P”,意思是“并非所有S是P”,可以表示成not all(S,P)这样的三分结构[21]。
可见,传统三段论主要讨论了涉及“所有的(all)”、“并非所有的(not all)”、“没有(no)”、“有些(some)”这四个亚氏量词的三段论的有效性。由于广义量词是亚氏量词的推广,亚氏量词是广义量词的特例,所以,广义量词理论对亚氏量词也是适用的[22]。因此,我们可以利用三分结构把所有的24个有效的传统三段论形式化如下:
[01]第一格AAA式:allE(M,P)且allE(S,M)⇒allE(S,P)
[02](第一格AAI式):allE(M,P)且allE(S,M)⇒someE(S,P)
[03]第一格AII式:allE(M,P)且someE(S,M)⇒someE(S,P)
[04]第一格EIO式:noE(M,P)且someE(S,M)⇒not allE(S,P)
[05]第一格EAE式:noE(M,P)且allE(S,M)⇒noE(S,P)
[06](第一格EAO式):noE(M,P)且allE(S,M)⇒not allE(S,P)
[07]第二格AEE式:allE(P,M)且noE(S,M)⇒noE(S,P)
[08](第二格AEO式):allE(P,M)且noE(S,M)⇒not allE(S,P)
[09]第二格EAE式:noE(P,M)且allE(S,M)⇒noE(S,P)
[10](第二格EAO式):noE(P,M)且allE(S,M)⇒not allE(S,P)
[11]第二格EIO式:noE(P,M)且someE(S,M)⇒not allE(S,P)
[12]第二格AOO式:allE(P,M)且not allE(S,M)⇒not allE(S,P)
[13]第三格EIO式:noE(M,P)且someE(M,S)⇒not allE(S,P)
[14]第三格OAO式:not allE(M,P)且allE(M,S)⇒not allE(S,P)
[15]第三格IAI式:someE(M,P)且allE(M,S)⇒someE(S,P)
[16]第三格AII式:allE(M,P)且someE(M,S)⇒someE(S,P)
[17]第三格AAI式:allE(M,P)且allE(M,S)⇒someE(S,P)
[18]第三格EAO式:noE(M,P)且allE(M,S)⇒not allE(S,P)
[19]第四格IAI式:someE(P,M)且allE(M,S)⇒someE(S,P)
[20]第四格EIO式:noE(P,M)且someE(M,S)⇒not allE(S,P)
[21]第四格AAI式:allE(P,M)且allE(M,S)⇒someE(S,P)
[22]第四格AEE式:allE(P,M)且noE(M,S)⇒noE(S,P)
[23](第四格AEO式):allE(P,M)且noE(M,S)⇒not allE(S,P)
[24]第四格EAO式:noE(P,M)且allE(M,S)⇒not allE(S,P)
其中,[2]、[6]、[8]、[10]和[23]这5个加括号的三段论称为弱式三段论,即:本可以推出全称命题,却得出特称命题的三段论;而[17]、[18]、[21]和[24]这4个三段论,只有在主项存在(即,前提的主项或谓项所指称的对象是存在的)的情况下,才是有效的,否则,是无效的三段论。
四、传统三段论的公理化
传统三段论第一格AAA式的具体形式是:所有M都是P,而且所有S都是M,所以,所有的S都是P;第一格EAE式的具体形式是:所有M都不是P,而且所有S都是M,所以,所有的S都不是P。正常的人仅仅凭直觉就可以判断这两个三段论是有效的,亚里斯多德学派很巧妙地选择了这两个不证自明的第一格的全称三段论作为传统三段论的公理。现在,笔者从第一格AAA式三段论的有效性和第一格EAE式三段论的有效性,来尝试推出其他22种有效的三段论。如果尝试成功,就说明我们完成了对传统三段论的公理化。
现在,我们可以利用广义量词理论来证明这两个公理的有效性。
(1)第一格AAA式三段论的形式化表示是:allE(M,P)且allE(S,M)⇒allE(S,P)。据亚氏量词的真值定义可知:allE(M,P)⇔M⊆P⊆E;且allE(S,M)⇔S⊆M⊆E。因此,由M⊆P⊆E且S⊆M⊆E可得S⊆P⊆E,据亚氏量词的真值定义可知S⊆P⊆E⇔allE(S,P)。故:allE(M,P)且allE(S,M)⇒allE(S,P)。即:第一格AAA式三段论是有效的。
(2)第一格EAE式三段论的形式化表示是:noE(M,P)且allE(S,M)⇒noE(S,P)。据亚氏量词的真值定义可知:noE(M,P)⇔M∩P=Ø;且allE(S,M)⇔S⊆M⊆E。因此,由M∩P=Ø且S⊆M⊆E可得S∩P=Ø,据亚氏量词的真值定义可知S∩P=Ø⇔noE(S,P)。故:noE(M,P)且allE(S,M)⇒noE(S,P)。即:第一格EAE式三段论是有效的。
(一)根据AAA-1三段论有效可以推出的有效三段论
第一格AAA式三段论有效,即:allE(M,P)且allE(S,M)⇒allE(S,P)。根据亚氏量词的真值定义可知allE(M,P)⇔M⊆P⊆E,因此,“allE(M,P)且allE(S,M)⇒allE(S,P)”成立,等价于M⊆P⊆E且allE(S,M)⇒allE(S,P)。根据单调性定义2(1)可知:all是右单调递增的。即:AAA-1三段论有效,当且仅当,all是右单调递增的。由此可以推出以下15个传统三段论有效。
(1)根据单调性关系定理可知,Q是右单调递增的,当且仅当,┓Q是右单调递减的;由于all与not all是互为外否定,根据单调性关系定理1(1)可知:all是右单调递增的,当且仅当,not all是右单调递减的,当且仅当,P⊆M⊆E且not allE(S,M)⇒not allE(S,P)(根据右单调递减的定义),当且仅当,allE(P,M)且not allE(S,M)⇒not allE(S,P)(根据all的真值定义)。即:第二格AOO式三段论有效。
(2)根据单调性关系定理可知,Q是右单调递增的,当且仅当,Q┓是右单调递减的;由于all与no是互为内否定,根据单调性关系定理1(2)可知:all是右单调递增的,当且仅当,no是右单调递减的,当且仅当,P⊆M⊆E且noE(S,M)⇒noE(S,P)(根据右单调递减的定义),当且仅当,allE(P,M)且noE(S,M)⇒noE(S,P)(根据all的真值定义)。即:第二格AEE式三段论有效。
(3)由于E命题和O具有从属关系,由“所有S都不是P(等价于没有S是P)”为真,可以得到“有S不是P(等价于并非所有的S是P)”为真,即:noE(S,P)⇒not allE(S,P)。因此,由(2)中的“allE(P,M)且noE(S,M)⇒noE(S,P)”,可得“allE(P,M)且noE(S,M)⇒not allE(S,P)”。即:第二格AEO式三段论有效。
(4)由于no具有对称性,根据对称性的定义可知:noE(S,M),当且仅当,noE(M,S)。因此,用noE(M,S)代换(2)中的“allE(P,M)且noE(S,M)⇒noE(S,P)”中的noE(S,M)。可得“allE(P,M)且noE(M,S)⇒noE(S,P)”。即:第四格AEE式三段论有效。
(5)与(3)的思路类似,由于E命题和O具有从属关系,即:noE(S,P)⇒not allE(S,P)。因此,由(4)中的“allE(P,M)且noE(M,S)⇒noE(S,P)”,可得“allE(P,M)且noE(M,S)⇒not allE(S,P)”。即:第四格AEO式三段论有效。
(6)根据单调性关系定理1(3)可知,Q是右单调递增的,当且仅当,Qd是右单调递减的;由于all与some是互为对偶否定,因此,all是右单调递增的,当且仅当,some是右单调递增的,当且仅当,M⊆P⊆E且someE(S,M)⇒someE(S,P)(根据右单调递增的定义),当且仅当,allE(M,P)且someE(S,M)⇒someE(S,P)(根据all的真值定义)。即:第一格AII式三段论有效。
(7)由(6)可知,第一格AII式三段论有效,即:allE(M,P)且someE(S,M)⇒someE(S,P),那么,根据命题变形规则“从(p&q→r)可以推出(┓r→┓(p&q))可以推出(┓r→(┓p∨┓q))可以推出(┓r→(p→┓q))可以推出(┓r&p→┓q)”,简言之,从(p&q→r)可以推出(┓r&p→┓q)。因此,从allE(M,P)且someE(S,M)⇒someE(S,P),可以推出┓someE(S,P)且someE(S,M)⇒┓(allE(M,P)),经过字母代换可得┓someE(M,P)且someE(M,S)⇒┓(allE(S,P))。又因为some与no是互为外否定,all与not all是互为外否定,因此,noE(M,P)且someE(M,S)⇒not allE(S,P)。即:第三格EIO式三段论有效。
(8)由(7)可知,第三格EIO式三段论有效,即:noE(M,P)且someE(M,S)⇒not allE(S,P)。又因为no具有对称性,根据对称性的定义可知:noE(M,P),当且仅当,noE(P,M)。这样,用noE(P,M)代替“noE(M,P)且someE(M,S)⇒not allE(S,P)”中的“noE(M,P)”,可得noE(P,M)且someE(M,S)⇒not allE(S,P)。即:第四格EIO式三段论有效。
(9)由(7)可知,第三格EIO式三段论有效,即:noE(M,P)且someE(M,S)⇒not allE(S,P)。又因为some具有对称性,根据对称性的定义可知:someE(M,S),当且仅当,someE(S,M)。这样,用someE(S,M)代替“noE(M,P)且someE(M,S)⇒not allE(S,P)”中的“someE(M,S)”,可得noE(M,P)且someE(S,M)⇒not allE(S,P)。即:第一格EIO式三段论有效。
(10)由(9)可知,第一格EIO式三段论有效,即:noE(M,P)且someE(S,M)⇒not allE(S,P)。又因为no具有对称性,根据对称性的定义可知:noE(M,P),当且仅当,noE(P,M)。这样,用noE(P,M)代替“noE(M,P)且someE(S,M)⇒not allE(S,P)”中的“noE(M,P)”,可得noE(P,M)且someE(S,M)⇒not allE(S,P)。即:第二格EIO式三段论有效。
(11)由(5)可知,第四格AEO式三段论有效,即:“allE(P,M)且noE(M,S)⇒not allE(S,P)”。与(7)的推理过程类似,根据命题变形规则“从(p&q→r)可以推出(┓r&p→┓q)”。因此,从allE(P,M)且noE(M,S)⇒not allE(S,P),可以推出┓(not allE(S,P))且allE(P,M)⇒┓(noE(M,S)),经过字母代换可得┓(not allE(P,M))且allE(M,S)⇒┓(noE(S,P))。又因为some与no是互为外否定,all与not all是互为外否定,因此,allE(P,M)且allE(M,S)⇒someE(S,P)。即:第四格AAI式三段论有效。
(12)由于A命题和I具有从属关系,由“所有S都是P”为真,可以得到“有S不是P”为真,即:allE(S,P)⇒someE(S,P)。因此,由于第一格AAA式三段论有效,即:“allE(M,P)且allE(S,M)⇒allE(S,P)”。故:allE(M,P)且allE(S,M)⇒someE(S,P)。即:第一格AAI式三段论有效。
(13)由(12)可知,第一格AAI式三段论有效,即:allE(M,P)且allE(S,M)⇒someE(S,P)。与(7)的推理过程类似,根据命题变形规则“从(p&q→r)可以推出(┓r&p→┓q)”。因此,由allE(M,P)且allE(S,M)⇒someE(S,P),可以推出┓(someE(S,P))且allE(S,M)⇒┓(allE(M,P)),经过字母代换可得┓(someE(M,P))且allE(M,S)⇒┓(allE(S,P))。又因为some与no是互为外否定,all与not all是互为外否定,因此,noE(M,P))且allE(M,S)⇒not allE(S,P)。即:第三格EAO式三段论有效。
(14)由于some具有对称性,根据对称性的定义可知:someE(S,M),当且仅当,someE(M,S)。因此,用someE(M,S)代换(6)中的“allE(M,P)且someE(S,M)⇒someE(S,P)”中的someE(S,M),可得allE(M,P)且someE(M,S)⇒someE(S,P)。即:第三格AII式三段论有效。
(15)由(11)可知,第四格AAI式三段论有效,即:allE(P,M)且allE(M,S)⇒someE(S,P)。与(7)的推理过程类似,根据命题变形规则“从(p&q→r)可以推出(┓r&p→┓q)”。因此,由allE(P,M)且allE(M,S)⇒someE(S,P),可以推出┓(someE(S,P))且allE(P,M)⇒┓(allE(M,S)),经过字母代换可得┓(someE(P,M))且allE(M,S)⇒┓(allE(S,P))。又因为some与no是互为外否定,all与not all是互为外否定,因此,noE(P,M))且allE(M,S)⇒not allE(S,P)。即:第四格EAO式三段论有效。
(二)根据EAE-1三段论有效可以推出的有效三段论
第一格EAE式三段论有效,即:noE(M,P)且allE(S,M)⇒noE(S,P)。根据亚氏量词的真值定义可知allE(S,M)⇔S⊆M⊆E,因此,“noE(M,P)且allE(S,M)⇒noE(S,P)”成立,等价于S⊆M⊆E且noE(M,P)⇒noE(S,P)。据单调性定义1(4)可知:no是左单调递减的。即:EAE-1三段论有效,当且仅当,no是左单调递减的。由此可推出以下7个传统三段论有效。
(16)根据单调性关系定理1(10)可知,Q是左单调递减的,当且仅当,┓Q是左单调递增的;由于no与some是互为外否定,因此,no是左单调递减的,当且仅当,some是左单调递增的,当且仅当,M⊆S⊆E且someE(M,P)⇒someE(S,P)(根据左单调递增的定义),当且仅当,someE(M,P)且allE(M,S)⇒someE(S,P)(根据all的真值定义)。即:第三格IAI式三段论有效。
(17)由于some具有对称性,根据对称性的定义可知:someE(M,P),当且仅当,someE(P,M)。因此,用someE(P,M)代换(16)中的“someE(M,P)且allE(M,S)⇒someE(S,P)”中的someE(M,P),可得“someE(P,M)且allE(M,S)⇒someE(S,P)”。即:第四格IAI式三段论有效。
(18)根据单调性关系定理1(12)可知,Q是左单调递减的,当且仅当,Qd是左单调递增的;由于no与not all是互为外否定,因此,no是左单调递减的,当且仅当,not all是左单调递增的,当且仅当,M⊆S⊆E且notE(M,P)⇒not allE(S,P)(根据左单调递增的定义),当且仅当,not allE(M,P)且allE(M,S)⇒not allE(S,P)(根据all的真值定义)。即:第三格OAO式三段论有效。
(19)由于no具有对称性,根据对称性的定义可知:noE(M,P),当且仅当,noE(P,M)。而第一格EAE式三段论有效,即:noE(M,P)且allE(S,M)⇒noE(S,P)。因此,用noE(P,M)代换“noE(M,P)且allE(S,M)⇒noE(S,P)”中的noE(M,P),可得“noE(P,M)且allE(S,M)⇒noE(S,P)”。即:第二格EAE式三段论有效。
(20)与(3)的思路类似,由于E命题和O具有从属关系,即:noE(S,P)⇒not allE(S,P)。因此,由(19)中的“noE(P,M)且allE(S,M)⇒noE(S,P)”,可得“noE(P,M)且allE(S,M)⇒not allE(S,P)”。即:第二格EAO式三段论有效。
(21)与(20)的思路类似,由于E命题和O具有从属关系,即:noE(S,P)⇒not allE(S,P)。而第一格EAE式三段论有效,即:noE(M,P)且allE(S,M)⇒noE(S,P)。故:noE(M,P)且allE(S,M)⇒not allE(S,P)。即:第一格EAO式三段论有效。
(22)由(20)可知,第二格EAO式三段论有效,即:noE(P,M)且allE(S,M)⇒not allE(S,P)。与(17)的推理过程类似,根据命题变形规则“从(p&q→r)可以推出(┓r&p→┓q)”。因此,从noE(P,M)且allE(S,M)⇒not allE(S,P),可以推出┓(not allE(S,P))且allE(S,M)⇒┓(noE(P,M)),经过字母代换可得┓(not allE(M,S))且allE(M,P)⇒┓(noE(S,P))。即:allE(M,P)且┓(not allE(M,S))⇒┓(noE(S,P))。又因为some与no是互为外否定,all与not all是互为外否定,因此,allE(M,P)且allE(M,S)⇒someE(S,P)。即:第三格AAI式三段论有效。
五、结语
根据以上的论述可见,笔者由AAA-1三段论的有效性和EAE-1三段论的有效性证明了其他22个有效的三段论(如下编号与文中证明的序号相对应,其中编号(1)—(15)三段论的有效性是根据AAA-1三段论的有效性推出来的,编号(16)—(22)三段论是根据EAE-1三段论的有效性推出来的),现在我们按照第一格至第四格有效三段论的顺序罗列如下:
(6)AII-1(9)EIO-1(12)AAI-1(21)EAO-1
(1)AOO-2(2)AEE-2(3)AEO-2(10)EIO-2(19)EAE-2(20)EAO-2
(7)EIO-3(13)EAO-3(14)AII-3(16)IAI-3(18)OAO-3(22)AAI-3
(4)AEE-4(5)AEO-4(8)EIO-4(11)AAI-4(17)IAI-4(15)EAO-4
而亚里斯多德学派认为,从AAA-1、EAE-1这两个三段论的有效性,可以推出除了预设了主项存在的三段论以外的其他所有的有效的传统三段论[1]228。即,可以证明,除去预设主项存在的AAI-3、AAI-4、EAO-3、EAO-4这4个三段论以外的18个三段论的有效性,而笔者利用广义量词理论证明了包括这4个三段论在内的22个三段论的有效性。很显然,笔者不仅证实了亚里斯多德学派的结论,而且还从AAA-1、EAE-1这两个三段论的有效性,证明了预设了主项存在的AAI-3、AAI-4、EAO-3、EAO-4这4个三段论的有效性,结果比预期的还要完美。
综上所述,笔者主要利用了广义量词理论对四个亚里斯多德量词的真值定义,在对传统三段论进行形式化的基础上,利用广义量词理论所揭示的四个亚里斯多德量词的单调性之间的转换关系,根据AAA-1和EAE-1这两个显而易见的公理,完成了对传统三段论的公理化这一艰巨的任务。这些创新性成果,对于中文信息处理以及计算机科学中的知识表示和知识推理,有着重要的意义。
[1]Westerståhl,D.uantifiers in Formal and Natural Languages[M]//D.M.Gabbay,F.Guenthner.Handbook of Philosophical Logic.Dordrecht:Kluwer Academic Publishers,2007.
[2]中国人民大学逻辑学哲学院逻辑学教研室.逻辑学(第三版)[M].北京:中国人民大学出版社,2014.
[3]林胜强,邹崇理.句法和语义的对应——语义形式化的基石[J].湖北大学学报:哲学社会科学版,2016,(1).
[4]张晓君.广义量词理论研究[M].厦门:厦门大学出版社,2014.
[5]于宇,唐晓嘉.汉语量化表达式的单调推理[J].湖北大学学报:哲学社会科学版,2012,(3).
[6]杜国平,邹崇理.逻辑在中国征信的基本途径[J].湖北大学学报:哲学社会科学版,2015,(1).
[7]桂起权.从逻辑哲学看辩证逻辑的形式化[J].湖北大学学报:哲学社会科学版,2014,(1).
[8]范丙申.逻辑与推理:事实重要吗[J].湖北大学学报:哲学社会科学版,2012,(3).
[9]张晓君,黄朝阳.基于广义量词理论的亚氏三段论的研究[J].重庆理工大学学报:社会科学版,2012,(10).
[10]Barwise,J.,Cooper,R.Generalized Quantifiers and Natural Language[M]//S.Davis,B.Gillon.Semantics:A Reader.Oxford:Oxford University Press,2004.
[11]林胜强,张晓君.广义量词的推理模式研究[J].湖南科技大学学报:社会科学版,2014,(6).
[12]张晓君.广义量词的语义性质研究[D].北京:中国社会科学院,2011.
[13]Barwise,J.,Cooper,R.Generalized Quantifiers and Natural Language[J].Linguistics and Philosophy,1981,4(2).
[14]Keenan,E.L.The Semantics of Determiners[M]//S.Lappin.The Handbook of Contemporary Semantic Theory.Oxford:Blackwell Publishing,1997.
[15]Peters S.,Westerst尖hl,D.Quantifiers in Language and Logic[M].Oxford:Claredon Press,2006.
[16]Szymanik,J.Quantifiers in Time and Space[M].Polen:Geboren te Warschau,2009.
[17]Moss,L.S.Syllogistic Logics with Verbs[J].Journal of Logic and Computation,2010,(4).
[18]Chow Ka Fat.Inferential Patterns of Generalized Quantifiers and their Applications to Scalar Reasoning[D].Hong Kong:Hong Kong Polytechnic University,2012.
[19]张晓君,吴宝祥.广义量词的单调性与其他语义性质之间的关系[J].重庆理工大学学报:社会科学版,2015,(1).
[20]张晓君,黄朝阳.广义量词的单调性与其三种否定量词的单调性之间的关系[J].安徽师范大学学报:人文社会科学版,2012,(6).
[21]张晓君,林胜强.基于广义量词理论的直言三段论推理规则的形式化辨析[J].中国社会科学院研究生院学报,2015,(1).
[22]张晓君.广义量词的相关性质研究[J].逻辑学研究,2010,(3).
[责任编辑:熊显长]
B81
A
1001-4799(2016)06-0032-07
2016-05-16
国家社会科学基金资助项目:15XYY012
张晓君(1970-),女,四川南充人,四川师范大学逻辑与信息研究所副研究员,哲学博士,主要从事自然语言逻辑、人工智能逻辑和Agent理论研究;李晟(1986-),男,四川德阳人,四川师范大学逻辑与信息研究所助教,哲学博士,主要从事现代逻辑、自然语言逻辑研究。
——对《物理学》8.6(259b1- 20)的一种解读
——“自由落体”教学中的物理学史辨
——《古希腊文化的集大成者亚里士多德》一课的教学思考与实践

