Gorenstein AC-投射复形的稳定性

赵仁育,权艳红

(西北师范大学数学与统计学院,甘肃兰州 730070)



Gorenstein AC-投射复形的稳定性

赵仁育,权艳红

(西北师范大学数学与统计学院,甘肃兰州 730070)

证明了以Gorenstein AC-投射复形为对象,利用定义Gorenstein AC-投射复形方法构造出的复形仍然是Gorenstein AC-投射复形.其次,引入了复形的Gorenstein AC-投射维数的概念,并对其进行了刻画.

Gorenstein AC-投射模;Gorenstein AC-投射复形;level复形;Gorenstein AC-投射维数

0 引言

近年来,Gorenstein同调代数受到了人们的极大关注[1-11].1998年,Enochs等[12]把 Gorenstein投射(内射)模的概念推广到了复形的范畴中,引入并研究了Gorenstein投射(内射)复形,称复形X是Gorenstein投射复形.如果存在投射复形的正合列

使得X≅Im(P0→P-1),且对任意的投射复形Q,Hom(P,Q)正合.对偶地,可以定义Gorenstein内射复形.随后,Gorenstein同调代数的许多结论被拓展到了复形范畴[3,11-15].作为平坦模和内射模的推广,Gao等[16]研究了弱平坦模和弱内射模,这两类模也被称为level模和AC-模[17].受Ding投射(内射)模[5-6]和Ding投射(内射)复形[14]研究思想的启发,Bravo等[17]研究了两类特殊Gorenstein复形——Gorenstein AC-投射复形和Gorenstein AC-内射复形,讨论了这两类复形与其各层次的模之间的关系.Xu等[11]证明了对复形X,若存在Gorenstein投射复形的正合列

使得X≅Im(P0→P1)，并且对任意的投射复形Q,Hom(P,Q)是正合复形,则X仍是Gorenstein投射复形,即Gorenstein投射复形是稳定的[11].受此结果的启发,在本文的第2节,我们讨论了Gorenstein AC-投射复形的稳定性,证明了以Gorenstein AC-投射复形为对象,利用定义Gorenstein AC-投射复形的方法构造出的复形仍然是Gorenstein AC-投射复形.在第3节中,通过引入复形Gorenstein AC-投射维数的概念,并对复形的Gorenstein AC-投射维数进行了刻画.对Gorenstein AC-内射复形有对偶的结果,本文不再赘述.

1 预备知识

将R-模的复形

记为(X,δ),简记为X.复形X的第n层次的循环(边缘,同调模)记作Zn(X)(Bn(X),Hn(X)).用Ch(R)代表R-模的复形构成的Abel范畴.设X,Y∈Ch(R),用Hom(X,Y)表示X到Y的所有复形态射构成的Abel群;对任意的i≥1,Exti(X,Y)表示Hom的右导出函子.用Hom(X,Y)表示由X和Y确定的Abel群的复形,它的第n层次为

第n层次的边缘算子是

设A是Abel范畴,X是A中一些对象的类,据文献[2],称X是投射可解的.如果X包含A的所有投射对象,并且对A中的任意短正合列0→A′→A→A″→0,若A″∈X,则A∈X当且仅当A′∈X.称A中对象的复形C是Hom(-,X)正合的,是指对任意的X∈X,复形Hom(C,X)是正合的.

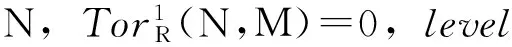
其中每个Pi是投射模,使得M≅Ker(P-1→P-2).由GorensteinAC-投射模的定义易见.

引理1 设M是模.则M是GorensteinAC-投射模,当且仅当对任意的level模F,Ext≥1(M,F)=0,并且存在Hom(-,L(R))正合的正合列

其中Pi都是投射模.

引理2GorensteinAC-投射模的类是投射可解的.

证明 类似于文献[10]定理2.6的证明可得. 】

称复形P是投射复形,如果P是正合复形,并且每个Zn(P)是投射模.据文献[17],称复形L是level复形,如果L是正合复形,并且每个Zn(L)是level模,将level复形的类记作L(Ch(R));称复形X是Gorenstein AC-投射复形,简称为GAC-投射复形,如果存在Hom(-,L(Ch(R))正合的正合列

其中每个Pi都是投射复形,使X≅Ker(P-1→P-2).

2 Gorenstein AC-投射复形的稳定性

本节讨论Gorenstein AC-投射复形的稳定性,为此先做一些准备工作.

引理3 由文献[17]中定理4.13，设X∈Ch(R).则X是GAC-投射复形当且仅当对任意的i∈Z,Xi是GAC-投射模,且对任意的level复形L,Hom(X,L)是正合复形.

引理4GAC-投射复形的类是投射可解的.

证明 显然,投射复形是GAC-投射复形.设0→X→Y→Z→0是复形的短正合列,其中Z是GAC-投射复形.设L是level复形,由level模的定义易见每个Li是level模.由引理3知每个Zj是GAC-投射模,所以由引理1,对任意的n,t∈Z,Ext1(Zt,Lt+n)=0.于是对任意的n,t∈Z,有短正合列

进而有复形的短正合列0→Hom(Z,L)→Hom(Y,L)→Hom(X,L)→0.由引理3,Hom(Z,L)是正合复形,所以由引理2和引理3可证得X是GAC-投射复形,当且仅当Y是GAC-投射复形,从而结论成立. 】

引理5GAC-投射复形的类关于直和项和任意直和封闭.

证明 设X是GAC-投射复形,且A⊕B=X.则由引理3知,对任意i∈Z,Ai是GAC-投射模.设L是level复形.则由引理3知,Hom(X,L)是正合复形.因为Hom(A⊕B,L)≅Hom(A,L)⊕Hom(B,L),所以Hom(A,L)正合.于是由引理3知,A是GAC-投射复形.

引理6 设0→X→Y→Z→0是复形的正合列.若X和Y是GAC-投射复形,则Z是GAC-投射复形,当且仅当对任意的level复形L,Ext1(Z,L)=0.

证明 必要性显然,现证充分性.因为X是GAC-投射复形,所以存在复形的正合列0→X→P→G→0,其中P是投射复形,G是GAC-投射复形.于是推出图

在短正合列0→Y→Q→G→0中,因为G和Y是GAC-投射复形,所以由引理4知,Q是GAC-投射复形.又因为P是level复形,所以Ext1(Z,P)=0.从而第二行的正合列可裂.由引理5知,Z是GAC-投射复形. 】

引理7 设

(1)

是复形的正合列,其中G1和G0是GAC-投射复形.则

1)存在正合列

(2)

和

(3)

其中J和P是投射复形,G和F是GAC-投射复形.

2)如果(1)是Hom(-,L(Ch(R)))正合的,那么(2)和(3)也是Hom(-,L(Ch(R)))正合的.

证明 1)因为G1是GAC-投射复形,所以存在正合列0→G1→J→Q1→0,其中J是投射复形,Q1是GAC-投射复形.考察推出图

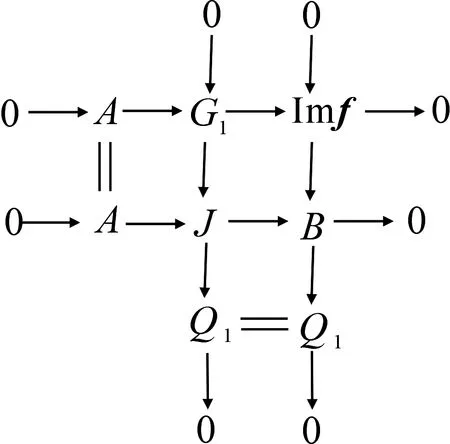
由第三列和短正合列0→Imf→G0→X→0,有下列推出图

由上面两个推出图的第二行得正合列0→A→J→G→X→0.在正合列0→G0→G→Q1→0,因为G0,Q1是GAC-投射复形,所以由引理4,G是GAC-投射复形.

因为G0是GAC-投射复形,所以存在正合列0→Q2→P→G0→0,其中P是投射复形,Q2是GAC-投射复形.考察拉回图

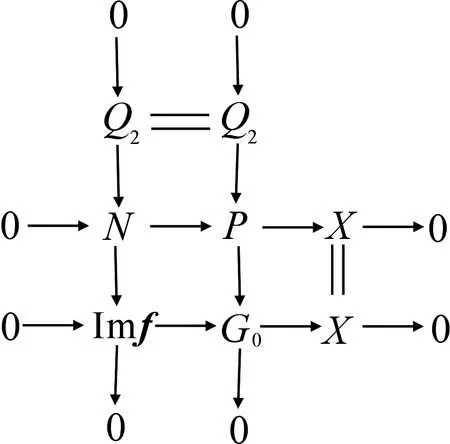
由该图中的第一列和短正合列0→A→G1→Imf→0,考察拉回图

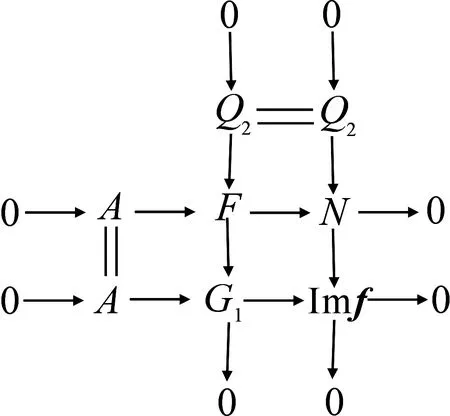
由以上两个拉回图的第二行得正合列

0→A→F→P→X→0,

并且由引理4,F是GAC-投射复形.

2)设L是level复形,并且(1)是Hom(-,L)正合的,则Ext1(Imf,L)=0.因为Q1是GAC-投射复形,所以Ext1(Q1,L)=0.从而Ext1(B,L)=0.故Hom(-,L)保持(2)的正合性.因为Ext2(X,L)=0且P是投射复形,所以Ext1(N,L)=0.Hom(-,L)保持(3)的正合性. 】

引理8 设n是正整数,

(4)

是复形的正合列,其中每个Gi是GAC-投射复形.则

1)存在复形的正合列

0→A→Pn-1→…→P1→P0→Y→0 (5)

和0→X→Y→U→0，其中每个Pi是投射复形,U是GAC-投射复形.

2)存在复形的正合列

0→B→Pn-1→…→P1→P0→X→0(6)

和0→V→B→A→0,其中每个Pi是投射复形,V是GAC-投射复形.

3)如果(4)是Hom(-,L(Ch(R)))正合的,那么(5)和(6)也是Hom(-,L(Ch(R)))正合的.

证明 1)对n进行归纳.

当n=1时,在正合列0→A→G0→X→0中,因为G0是GAC-投射复形,所以存在正合列0→G0→P0→U→0,其中P0是投射复形,U是GAC-投射复形.于是由推出图

可得所需的正合列0→A→P0→Y→0和0→X→Y→U→0.

设n≥2且有正合列

其中每个Gi是GAC-投射复形.令K=Coker (Gn-1→Gn-2).则有正合列

和

0→K→Gn-3→…→G1→G0→0.

由引理7知存在正合列

由归纳假设,存在正合列

0→A′→Pn-2→Pn-3→…→P1→P0→X→0

和

0→X→Y→U→0,

其中每个Pi是投射复形,U是GAC-投射复形.于是有正合列

其中每个Pi是投射复形.

2)类似于1)可证.

3)设L是level复形,并且Hom(-,L)保持(4)的正合性.当n=1时,上面推出图的第一行与第二列是Hom(-,L)正合的,故第二行是Hom(-,L)正合的.当n≥2时,由引理7及归纳假设可得(5)是Hom(-,L)正合的.(6)的Hom(-,L(Ch(R)))正合性类似可证. 】

定理1 设X∈Ch(R).则X是GAC-投射复形当且仅当存在GAC-投射复形的正合列

使得X≅Cokerσ1并且对任意的level复形L,Hom(G,L)正合.

证明 ⟹.显然.

⟸.设存在Hom(-,L(Ch(R)))正合的GAC-投射复形的正合列

使得X≅Imσ0.对任意的i∈Z,令Xi=Imσi.则X0=X,并且对任意的i∈Z,有Hom(-,L(Ch(R)))正合的正合列0→Xi+1→Gi→Xi→0.下面证明X是GAC-投射复形.

考察正合列

由引理8,存在Hom(-,L(Ch(R)))正合的正合列

和

其中P-1是投射复形,V-1是GAC-投射复形.于是由推出图

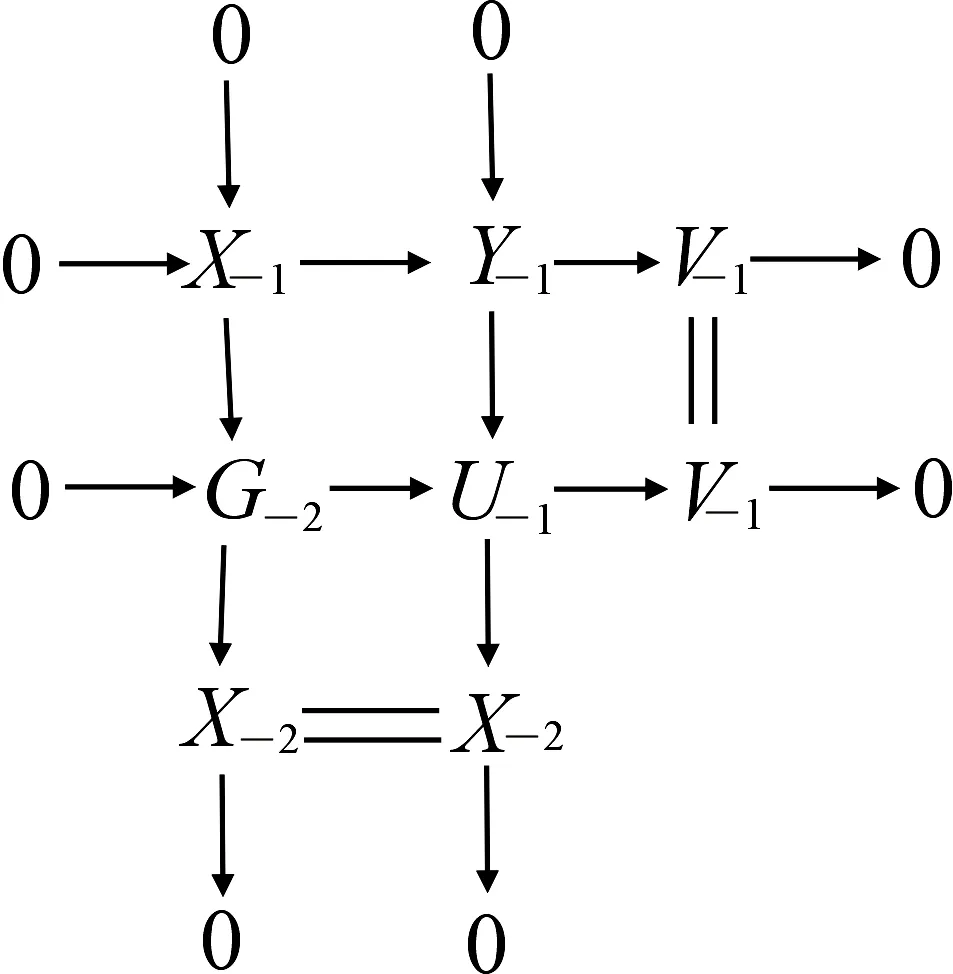
可得正合列

因为G-2和V-1是GAC-投射复形,所以由引理4知,U-1是GAC-投射复形.因为

是Hom(-,L(Ch(R)))正合的,所以

是Hom(-,L(Ch(R)))正合的.重复上述过程可得Hom(-,L(Ch(R)))正合的正合列

其中P-i是投射复形,i=1,2,…,Y0=X.于是有Hom(-,L(Ch(R)))正合的正合列

(*)

其中每个P-i是投射复形.

对偶地,可以证明存在Hom(-,L(Ch(R)))正合的正合列

(**)

其中每个Pi是投射复形.

由(*)和(**)得Hom(-,L(Ch(R)))正合的正合列

其中每个Pi是投射复形,使得X≅Im(P0→P-1).因此X是GAC-投射复形. 】

3 复形的Gorenstein AC-投射维数

作为引理7的另一个应用,本节研究复形的Gorenstein AC-投射维数.因为投射复形是GAC-投射复形,所以每个复形都有GAC-投射分解,从而可以定义复形的GAC-投射维数.

引理9 设X∈Ch(R).考察复形的正合列

证明 作映射锥,得复形的正合列

进而有复形的正合列

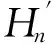
推论1 设X∈Ch(R).考察复形的正合列

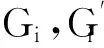
证明 由引理9可得. 】

定理2 设X∈Ch(R),n≥0.则以下条件等价:

1)GAC-pd(X)≤n;

2)GAC-pd(X)<∞,且对任意level维数有限的复形L,Ext>n(X,L)=0;

3)GAC-pd(X)<∞,且对任意level复数L,Ext>n(X,L)=0;

4)对复形的任意正合列…→Gn→Gn-1→…→G0→X→0,其中每个Gi是GAC-投射复形,Kn=Ker(Gn-1→Gn-2)是GAC-投射复形;

5)对任意的0≤t≤n存在正合列0→Pn→…→Pt+1→Gt→Pt-1→…→P0→X→0,其中Gt是GAC-投射复形,Pi是投射复形.

证明 2)⟹3),4)⟹5)和5)⟹1)显然.

1)⟹2).因为GAC-pd(X)≤n,所以存在X的长度为n的GAC-投射分解

由维数转移,对任意的m>n和任意的level维数有限的复形L,Extm(X,L)≅Extm-n(Gn,L)=0.

3)⟹4).设

是X的一个GAC-投射分解.下证Kn=Ker(Gn-1→Gn-2)是GAC-投射复形.

由3),设GAC-pd(X)=m<∞.则存在X的长度为m的GAC-投射分解

i)若m≤n,将上述X的GAC-投射分解扩充为长度为n的GAC-投射分解

由推论1知,Kn是GAC-投射复形.

1)⟹5).对n进行归纳.

当n=1时,存在正合列0→D1→D0→X→0,其中D0,D1是GAC-投射复形.由引理7(A=0的情形),存在正合列0→P1→G0→X→0和正合列0→G1→P0→X→0,其中G0,G1是GAC-投射复形,P0,P1是投射复形.故n=1时结论成立.

设n≥2,且有复形的正合列0→Dn→Dn-1→…→D0→X→0,其中每个Di是GAC-投射复形.令A=Ker(D1→D0).则有正合列

0→A→D1→D0→X→0.

令Y=Ker(P0→X).则GAC-pd(Y)≤n-1.由归纳假设,存在正合序列

其中Gt是GAC-投射复形,Pi是投射复形,i=0,1,…,t-1,t+1,…,n.下面证明t=0的情形.令B=Coker(D2→D1),由归纳假设,存在正合列

由引理7,存在正合列0→C→P1→G0→X→0,其中G0是GAC-投射复形,P1是投射复形.于是有正合序列

其中Pi是投射复形,i=1,2,…,n. 】

推论2 设0→X′→X→X″→0是复形的短正合列,n∈N.则

1)若GAC-pd(X″)≤n,则GAC-pd(X′)≤n当且仅当GAC-pd(X)≤n.进而,

GAC-pd(X′)≤max{GAC-pd(X),GAC-pd(X″)},

GAC-pd(X)≤max{GAC-pd(X′),GAC-pd(X″)}.

2)若GAC-pd(X′)>GAC-pd(X″)或GAC-pd(X)>GAC-pd(X″),则GAC-pd(X′)=GAC-pd(X).

3)若GAC-pd(X″)>0,X是GAC-投射复形.则GAC-pd(X′)=GAC-pd(X″)-1.

因此,在0→X′→X→X″→0中,如果任意两项的GAC-投射维数有限,那么第三项的GAC-投射维数也有限.

证明 1)当n=0时,X″是GAC-投射复形.于是由引理4知,X′是GAC-投射复形当且仅当X是GAC-投射复形.故n=0时结论成立.

假设n>0.作X′,X″的投射分解

由马掌引理有以下交换图

2)设GAC-pd(X′)>GAC-pd(X″).则由1)中的第二个不等式知,GAC-pd(X)≤GAC-pd(X′).若GAC-pd(X)

由1),2),3),最后一个事实成立. 】

[1] ENOCHS E E,JENDA O M G.Gorenstein injective and projective modules[J].MathZ,1995,220(1):611.

[2] ENOCHS E E,JENDA O M G.RelativeHomologicalAlgebra[M].Berlin:Walter de Gruyter,2000.

[3] CHRISTENSEN L W.GorensteinDimension[M].Berlin:Springer,2000.

[4] HOLM H.Gorenstein homological dimensions[J].JPureApplAlgebra,2004,189(1):167.

[5] DING N Q,LI Y L,MAO L X.Strongly Gorenstein flat modules[J].JAustMathSoc,2009,86(3):323.

[6] DING N Q,MAO L X.Gorenstein FP-injective and Gorenstein flat modules[J].JAlgebraAppl,2008,7(4):491.

[7] GILLESPIE J.Model structures on modules over Ding-Chen rings[J].Homology,HomotopyAppl,2010,12(1):61.

[8] HUANG C H,HUANG Z Y.Gorenstein syzygy modules[J].JAlgebra,2010,324(12):3408.

[9] GENG Y X,DING N Q.W-Gorenstein modules[J].JAlgebra,2011,325(1):132.

[10] YANG G,LIU Z K,LIANG L.Ding projective and Ding injective modules[J].AlgebraColloq,2013,20(4):601.

[11] XU A M,DING N Q.On stability of gorenstein categories[J].CommAlgebra,2013,41(7):3793.

[12] ENOCHS E E,GARCA ROZAS J R.Gorenstein injective and projective complexes[J].CommAlgebra,1998,26(5):1657.

[14] YANG G,LIU Z K,LIANG L.Model structures of complexes over Ding-Chen rings[J].CommAlgebra,2013,41(1):50.

[15] XIN D W,CHEN J L,ZHANG X X．Completely W-Resolved complexes[J].CommAlgebra,2013,41(4):1247.

[16] GAO Z H,WANG F G.Weak injective and weak flat modules[J].CommAlgebra,2015,43(9):3857.

[17] BRAVO D,GILLESPIE J.Absolutely clean,level,and Gorenstein AC-injective complexes[EB/OL].[2015-07-28]http://arxiv.org/pdf/1408.7089v/.pdf.

(责任编辑 陆泉芳)

On stability of Gorenstein AC-projective complexes

ZHAO Ren-yu,QUAN Yan-hong

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

In this paper,it is proved that an iteration of the procedure used to define Gorenstein AC-projective complexes yields exactly Gorenstein AC-projective complexes.We also introduce and characterize the notion of the Gorenstein AC-projective dimension of complexes.

Gorenstein AC-projective modules;Gorenstein AC-projective complexes;level complexes;Gorenstein AC-projective dimension

10.16783/j.cnki.nwnuz.2016.01.001

2015-08-05;修改稿收到日期:2015-10-29

国家自然科学基金资助项目(11361052)

赵仁育(1977—)，男，甘肃景泰人，副教授，博士.主要研究方向为环的同调理论.

E-mail:zhaory@nwnu.edu.cn

O 153.3

A

1001-988Ⅹ(2016)01-0001-07