具有可选服务的M/M/1排队驱动的流模型
徐秀丽, 王现英,李晓庆
(燕山大学理学院,河北秦皇岛 066004)
具有可选服务的M/M/1排队驱动的流模型
徐秀丽, 王现英,李晓庆
(燕山大学理学院,河北秦皇岛 066004)
在驱动系统中添加一种服务规则,研究第二次服务可选的M/M/1排队系统驱动的流模型,流体的净输入率由驱动系统的外部环境控制.首先给出无穷小生成元矩阵,确定净输入率的结构;然后,使用Laplace变换(LT)方法得到库存量平稳分布的Laplace-Stieltjes变换(LST)及平均库存量的表达式.最后,通过数值实验讨论了参数的可行性及对系统性能指标的影响.
流模型;可选服务;平稳分布;无穷小生成元;Laplace变换(LT)
在发达的网络社会,网络交易已成为人们最重要的的交易活动之一,网上转账、汇款、缴费、购物等都是我们日常生活必不可少的一部分.就网上缴费来说,当完成缴费以后,再一次对话费余额进行查询就可以理解为第二次服务,也就是可选服务,由此可见,对可选服务的研究具有很广泛的实际意义.Mandan[1]首先应用补充变量的方法研究了具有二次可选服务的一般排队模型;Medhi[2]对文献[1]做了改进,更一般化地分析了服务时间的分布情况,得到了模型的性能指标;田乃硕等[3]结合广义时间提出嵌入马尔可夫链的方法,研究了第二次服务可选的单重休假离散排队系统.
快速发展的高科技时代,流排队模型的研究也具有很重要的实际意义.2009年,Bckker等[4]研究了通讯数据传输的流模型;关于M/M/1流排队模型的研究源于Virtamo和Narros[5],他们在有限环境中延伸了谱方法,讨论了一类M/M/1驱动流排队模型;Ramaswami[6]提出了一种矩阵解析方法,验证了流模型与拟生灭过程之间的联系,完善了文献[5]的工作;Mao等[7]分析了多重休假及N策略的驱动流排队模型,并获得了一些可行性的系统性能指标;梅宁等[8]研究了具有负顾客的M/M/1排队系统驱动的流模型;刘晓艳等[9]在文献[8]的基础上引入多重休假,并得到了相应的理论结果;Xu等[10]分析了关于工作休假的M/M/c排队驱动的流模型.
本文在外部驱动系统中考虑一种新的服务模式,通过研究第二次服务模式具有可选性的M/M/1排队系统驱动的流模型,建立净输入率结构,分析系统的各项性能指标,并尽可能得到符合实际意义的变量参数.
1 驱动系统的基本描述
本文讨论一类流模型,假设该模型缓冲器的容量是无限的,并且其净输入率结构由外部的驱动过程控制,设{L(t),t≥0}是排队系统中的队长.对于外部驱动过程做如下描述:
( i )系统中的顾客都以参数为λ(λ>0)的Poisson流到达;
( ii )假定每一次的服务时间都符合负指数分布;
(iii)到达的顾客都需要接受第一次服务,设定μ1(μ1>0)为第一次的服务率,在第一次服务完成后,顾客要么会以概率p留在系统要求接受第二次服务,要么以概率1-p离开系统,设定μ2(μ2>0)为第二次服务的服务率;
(iv)系统中任意顾客的到达时间间隔、接受服务的时间均相互独立,服务规则为先到先服务(FCFS).
设L(t)表示系统中的顾客数,那么{L(t),t≥0}便是一种可数状态空间上的马氏过程,状态空间为Ω={0,1,2,…},无穷小生成元

其中
当该模型的驱动系统的负载ρ=λ/M<1时,平稳队长L(t)服从参数为ρ的几何分布,且

2 流模型的平稳条件
假设在时刻t下缓冲器的库存量是X(t),且X(t)是一非负随机变量,缓冲器的净输入率(输入率-输出率)结构可以用随机过程{(X(t),L(t)),t≥0}的函数表达,即
其中σ<0,σ1>0.
上述表达式说明,当系统的驱动过程处于闲期时,库存量以速率σ减少,直到缓冲器容量为零,并保持零值不变;反之,处于忙期时,库存量以速率σ1增加.
二次可选服务的M/M/1排队系统驱动的流模型在一定意义上可以看作是二维Markov过程{(X(t),L(t)),t≥0},状态空间是具有混合型(连续×离散)的:Ω=[0,+∞)×{0,1,2,…}.当t→∞时,X(t)有唯一的极限分布,流模型的平均净输入率d(平均漂移)应为负值,即
当d<0时,流模型表现出一种平衡的状态.也就是说,如果缓冲器的容量是无限大,那么Markov过程{(X(t),L(t)),t≥0}的平衡条件为ρ<1及d<0同时成立.
3 基本方程及其解
引入联合分布,设
假定流模型的驱动过程平衡时,{(X(t),L(t)),t≥0}收敛到随机变量(X,L),其中X,L分别是稳态下系统的库存量及任意时刻的顾客数.记(X,L)的联合分布为
则稳态下库存量的分布函数为
为了简便计算,F(x)可用向量表示为
那么F(x)满足矩阵微分方程
(1)
同时满足边界条件Fj(t,x)=P{X=0,L=0}=a,Fj(0)=0,j≥1,其中Λ=diag(σ,σ1,…)为漂移矩阵,a为稳态下的流模型的空库概率.
引入联合分布的Laplace变换,记Fj(x)和F(x)的Laplace变换分别为:
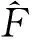
(2)
4 稳态分布及均值
引理1 若ρ<1,则二次方程
存在两个不同实根r0(s)与r1(s),满足0 定理1 如果流模型稳定,且d<0和ρ<1同时成立,那么稳态联合分布的Laplace变换为 (3) 并且库存量平稳分布F(x)的Laplace变换为 (4) 证明 差分方程组(2)可以表示成 从第一个方程式,解得 由引理1知,r0(s)是方程 的根,所以 引入Fj(s)的联合分布的Laplace-Stieltjes变换,记为 库存量平稳分布F(x)的Laplace-Stieltjes变换为 (5) 定理2 如果流模型稳定,即d<0及ρ<1成立,则库存量稳态分布的Laplace-Stieltjes变换和均值分别为 (6) (7) 其中d=σ(1-ρ)+σ1ρ是平均漂移. 证明 联立(4)和(5)式,可得 (8) 由正规化条件及r0(s)=ρ可得 所以a=d/σ,代入(8)式,整理即得(6)式. 对(6)式两边同时关于s求导,令s=0,结合引理1,得 所以(7)式成立. 】 当系统中某些参数变动时,我们讨论流模型的稳态库存量及空库概率的变化情况.设定参数值λ=2,σ1=3,μ1=μ2=4,当确定净输入率σ时,图1说明,空库概率a随着概率p的增大而增大;图2说明,平均库存量E(X)随着概率p的减少而增大.当确定概率p时,图1说明,空库概率a将会随着净输入率p的减少而增大;图2说明,平均库存量E(X)将会随着净输入率σ的增大而增大.所以,参数值发生变化时,流模型的稳态库存量及空库概率都将随之发生变动. 图1 空库概率a随p和σ的变化Fig 1The curves of a with the change of p and σ 图2 平均库存量E(X)随p和σ的变化Fig 2The curves of E(X) with the change of p and σ 本文给出了一种新的外部驱动环境,进而建立了对应的流模型.同时,提出了流模型的净输入率 结构,利用Laplace变换方法给出了流模型的稳态性能指标的表达式,是对经典的M/M/1排队系统驱动流模型的推广.最后,通过Matlab数值分析,讨论了流模型性能指标随系统参数的变化情况,具有一定的实际意义. [1]MANDANKC.AnM/G/1Queuewithsecondoptionalservice[J].Queuing Systems,2000,34(1-4):37. [2] MEDHI J.A single sever poisson input queue with a second optional channel[J].QueuingSystems,2002,42(3):239. [3] 田乃硕,赵媛,康小娟.第二次服务可选的单重休假离散排队系统[J].西北师范大学学报(自然科学版),2010,46(3):19. [4] BCKKER R,MENDJES M.A fluid model for a relay node in an ad hoc network:the case of heavy-tailed input[J].MathMethodsOperaRes,2009(70):357. [5] VIRTAMO J,NORROS I.Fluid queue driven by an M/M/1 queue[J].QueuingSystems,1994,16(3/4):373. [6] RAMASWAMI V.Matrix analytic methods for stochastic fluid flows[C]//Proceedingsofthe16thInternationalTeletrafficCongress.Edingurgh:ROYAUME-UNI,1999:1019. [7] MAO B,WANG F,TIAN N.Fluid model driven by an M/M/1 queue with multiple vacations and N-policy[J].JournalofAppliedMathematicsandComputing,2012,38(1-2):119. [8] 梅宁,徐秀丽,刘晓艳.具有负顾客的M/M/1排队系统驱动的流模型[J].辽宁工程技术大学学报(自然科学版),2014,33(1):116. [9] 刘晓艳,梅宁,徐秀丽.带负顾客的M/M/1多重休假排队系统驱动的流模型[J].西北师范大学学报(自然科学版),2013,49(5):25. [10] XU X,GENG J,LIU M,et al.Stationary analysis for the fluid model driven by the M/M/c working vacation queue[J].JournalofMathematicalAnalysisandApplications,2013,403(2):423. (责任编辑 马宇鸿) Fluid model driven by an M/M/1 queue with optional service XU Xiu-li, WANG Xian-ying,LI Xiao-qing (School of Science,Yanshan University,Qinhuangdao 066004,Hebei,China) In this paper,a fluid model driven by an M/M/1 queue with optional service is considered,where the net input rate of fluid is controlled by the drive system of the external environment.Firstly,the infinitesimal generator is given,and the structure of net input rate of fluid is determined.Secondly,using the Laplace transform(LT) method,a smooth buffer content distribution of the Laplace-Stieltjes transform(LST) and the average buffer content formula are given.Finally,the numerical results of the model are presented. fluid model;optional service;stationary distribution;infinitesimal generator;Laplace transform(LT) 10.16783/j.cnki.nwnuz.2016.01.005 2015-01-27;修改稿收到日期:2015-07-16 国家自然科学基金资助项目(11201408);河北省自然科学基金资助项目(A2013203148) 徐秀丽(1976—),女,辽宁北票人,教授.主要研究方向为随机模型及性能分析. E-mail:xxl-ysu@163.com O 226 A 1001-988Ⅹ(2016)01-0021-04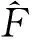
5 数值分析
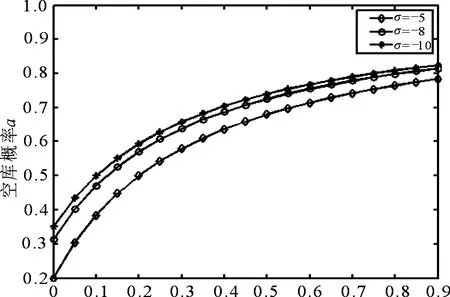
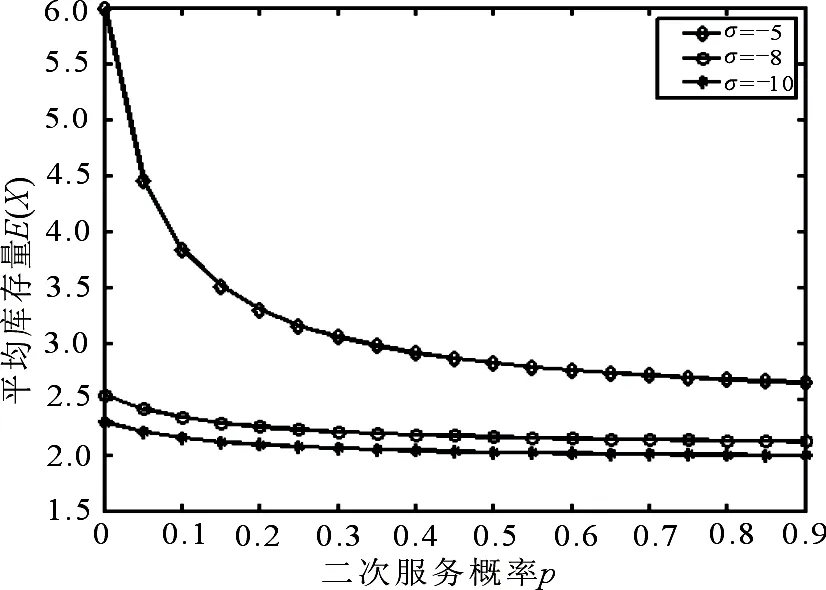
6 结论

