一种特殊家庭联合保险的精算模型研究
关清元,陶菊春
(1.武夷学院数学与计算机学院,福建武夷山 354300;2.西北师范大学数学与统计学院,甘肃兰州 730070)
一种特殊家庭联合保险的精算模型研究
关清元1,陶菊春2
(1.武夷学院数学与计算机学院,福建武夷山 354300;2.西北师范大学数学与统计学院,甘肃兰州 730070)
为了消除利率随机性所产生的风险,对随机利率采用AR(1)模型建模,以一种特殊家庭联合保险模型为基础,讨论了多元生存函数,给出了保额的精算现值及其均衡年保费的计算方法.
精算现值;均衡保费;寿险;年金;AR(1)模型
0 引言
现阶段,学术界对寿险精算模型的研究大多数都是确定利率环境下的一些结论.1998年,吴耀华等[1]探讨了确定利率下夫妻联合养老保险的保费准备金的计算问题.2004年,王丽燕、冯恩民探讨了确定利率下家庭联合保险的保费计算问题.然而现实生活中,实际的利率都是变化的,所以也有一批学者对寿险和年金中死亡率与利率均为随机的情况进行了专门的研究[2-6].本文通过对随机利率采用AR(1)模型建模,以家庭联合保险模型为基础[7],讨论随机利率下的一种具有养老性质的单亲家庭的家庭联合保险的精算问题,并推导其年均衡纯保费的计算公式.
1 承保对象及其保险责任
1.1 承保对象
年龄为1~10周岁的独生子女,其父(或母)由于某种原因死亡,其跟随25~35周岁的母(父)以及50~60(外)祖父母一起生活的单亲家庭.
1.2 保险责任
1.2.1 寿险 若其父(或母)以及其(外)祖父母三方任何一人在保单生效后死亡,则在死亡即刻给付保险金R1;若此独生子女先于其父(或母)以及其(外)祖父母死亡,则在死亡时即刻给付保险金a1R1(a1>3),若后于其父(或母)及其(外)祖父母死亡,则不给付保险金.
1.2.2 年金 若其父(或母)以及其(外)祖父母三方任何一方生存至60周岁(或55周岁)时开始给付养老金,至三方全部死亡时为止.养老金每年年初给付,以(x)表示年龄为x的被保险人,假设此独生子女的年龄为z,其父(或母)的年龄为w,其(外)祖父母双方的年龄分别为x和y,不妨设z (i)在投保后第n年至第m年(m>n),若(x),(y)至少有一人活着,(w)与(z)都活着,则每年支付R2. (ii)在投保后第n年至第m年,若(x),(y)均死亡,而(w)与(z)都活着,则在第二个死亡发生时刻,每年支付R3. (iii)在第m年至第η年间,若(x),(y)至少有一人活着,(w)与(z)也活着,则每年支付a2R2(R2是正常退休金的1.5~2倍,且按人头数发放). (iv)在第m年至第η年间,若(x),(y)均死亡(以第二个死亡日期为准),(w)活着而z<18,则每年支付a3R3至z=18(a3>1). (v)若η年后,(x),(y),(w)均死亡,则每年支付R4,至最后一人死亡为止. 考虑三个生命(x),(y),(z)的情形,以及四个生命(x),(y),(z),(w)的情形.按惯例,以T(x)表示(x)的未来寿命(或未来余命),tqx=P(T(x)≤t)=1-P(T(x)>t)(t≥0)为(x)在t年内死亡的概率,K(x)=[T(x)]来表示(x)未来寿命的周年数或(x)在未来生存的整年数,即K(x)是T(x)的最大整数部分[8],用μx表示在x岁时的死力(也称瞬间死亡率或死亡密度). 2.1 多生命的联合生存状态与最后生存状态 2.1.1 联合生存状态 当且仅当(x),(y),(z)都生存时状态存续,只要其中有一个死亡时即消亡的状态.此时把一个x岁的生命(x)和一个y岁的生命(y)以及一个z岁的生命(z)组成的状态称为联合生存状态,这种状态记为(xyz),T(xyz)表示联合生存状态(xyz)的余命,即T(xyz)=min(T(x),T(y),T(z)).对于联合生存状态(xyz),在T(x),T(y),T(z)相互独立的条件下,有 (1) 故有 FT(t)=1-tpxyz. (2) 从而T(xyz)的密度函数为 (3) (4) 此时 (5) (6) 四元联合生存状态可记为(xyzw),此种情况类似于三元联合生存状态,在T(x),T(y),T(z),T(w)相互独立的条件下,也有类似结果tpxyzw=tpx·tpy·tpz·tpw. 2.2 多生命的条件生存状态[9] (7) 针对利息力累积函数,当利率满足AR(1)[10]模型时,即 (8) 其中,δt代表第t年的利率,-1<φ<1,{εt}是相互独立的均值为0、方差为σ2的同正态分布序列,即εt~N(0,σ2),所以 (9) (10) 此处假设δ(t)与T(x),T(y)相互独立. 假设缴费期为h(h≤min(m,n,η,λ))年,保费在(x),(y),(z),(w)都活着时年初缴付,下面先按照寿险和年金两种情形分别计算被保险人未来收益的精算现值和均衡年缴纯保费,再求和即得总保费. 4.1 寿险 (11) 对非单个的寿险来说,可以先设其死亡受益金为1,则其责任可视为如下三部分的组合: (a)在三元联合生存状态(xyw)终止时,受益金为1; (c)在四生命条件存在状态结束时受益金为1. (12) (13) (14) 均衡年保费是h年内当(xyzw)存在时每年年初支付的,第k(0≤k≤h)年的受益金为1的精算现值为 (15) 根据平衡原理,投保时趸缴保费的精算现值应与均衡年保费的精算现值相等,从而得到平衡方程 (16) 同理可得 (17) 4.2 年金 方式( i )是该年金(xyw)延期n年的定期(m-n)年的年金[6],其精算现值为 (18) 其均衡年保费为 (19) 故 (20) 故 (21) (22) (22)式上标中两个2表示(z),(w)均在(x)与(y)中的残存者之后死亡. 方式(v)的精算现值和均衡年保费分别为 (23) 综上可得,保单的均衡年保费为 (24) 其中a1>3,a2,a3>2. 本文设计并讨论了一种具有养老性质的单亲家庭的投保问题,首次给出了随机利率下该种情况的家庭联合保险的保额的精算现值及其均衡年保费的计算方法,并推导出了相应的公式,具有一定的创新性和实用价值. [1] 吴耀华,蔡新中,吴之强.一种夫妻联合养老金(付死亡)保险的计算问题[J].中国科学技术大学学报,1998,28(4):439. [2] BEEKMAN J A,FUELLING C P.Interest and mortality randonmess in some annuities[J].Insurance:MathematicsandEcomomics,1990,9:185. [3] BEEKMAN J A,FUELLING C P.Extra randomness in certain annuity models[J].Insurance:MathematicsandEconomics,1991,10:275. [4] De SCHEPPER A,De VYLDER F,GOOVAERTS M,et al.Interest randomness in annuities certain[J].Insurance:MathematicsandEconomics,1992,11:271. [5] De SCHEPPER A,GOOVAERTS M.Some further results on annuities certain with random interest[J].Insurance:MathematicsandEcomomics,1992,11:283. [6] De SCHEPPER A,GOOVAERTS M,DELBAEN F.The Laplace transtorm of annuities certain with exponential time distribution[J].Insurance:MathematicsandEcomomics,1992,11:291. [7] 王丽燕,柳杨.一种家庭联合保险的精算模型[J].大连大学学报,2004,25(2):45. [8] 卢仿先,曾庆五.寿险精算数学[M].天津:南开大学出版社,2001. [9] 张波.应用随机过程[M].北京:中国人民大学出版社,2000. [10] 王晓军.企业养老金计划精算模型[J].统计研究,2003(2):24. [11] 刘新红.随机利率下一种家庭联合保险的精算模型[J].北京石油化工学院学报,2007,15(3):56. (责任编辑 马宇鸿) A special family coinsurance actuarial model GUAN Qing-yuan1,TAO Ju-chun2 (1.College of Mathematics and Computer,Wuyi University,Wuyishan 354300,Fujian,China;2.College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China) In order to eliminate interest rate risk arising from randomness,a family coinsurance model is established based on the random rate dertermied byAR(1) model,the multiple survival function is discussed,and the actuarial present value of the insured amount and equilibrium premiums are given. actuarial present value;equilibrium premiums;life insurance;annuity;AR(1) model 10.16783/j.cnki.nwnuz.2016.01.007 2015-04-20;修改稿收到日期:2015-08-25 武夷学院科技类项目(XL1202,XD201405) 关清元(1981—),男,河南信阳人,讲师,硕士.主要研究方向为计算数学与保险精算. E-mail:441729707@qq.com F 840 A 1001-988Ⅹ(2016)01-0031-042 多生命函数

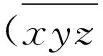
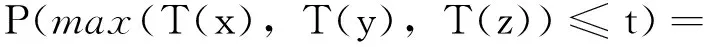



3 利息随机性的建模
4 纯保费的计算