Bargmann-Segal空间刻画Banach空间值广义泛函
周玉兰,王玄静
(西北师范大学数学与统计学院,甘肃兰州 730070)
Bargmann-Segal空间刻画Banach空间值广义泛函
周玉兰,王玄静
(西北师范大学数学与统计学院,甘肃兰州 730070)
引入Banach空间值Bargmann-Segal空间E2(v,X),其中v是广义函数空间E*C上的复Gauss测度,X是一个可分自反Banach空间.借助于指数向{ε(ξ):ξ∈Dp}的完全性,通过广义算子象征方法,应用E2(v,X)讨论了Banach空间值广义泛函L[Gp,X]的解析刻画,其中p∈R.同时,应用广义泛函在E2(v,X)中的Hilbert范数计算了向量值广义算子T∈L[Gp,X]的算子范数.
白噪声分析;Banach空间值Bargmann-Segal空间;广义泛函;解析刻画
0 引言
标量值白噪声广义泛函的解析刻画是一个很有用的工具[1-4],近年来,向量值广义泛函在白噪声分析应用中扮演了更加重要的角色.
向量值广义泛函的象征存在很多优点:Wang[5]及Ji-Obata[6]考虑了一个G*值广义泛函的解析刻画,其中G*是可列Hilbert空间G的对偶空间;王才士等[7]讨论了Banach空间值广义泛函的解析刻画;Grothaus等[8]给出了Bargmann-Segal空间广义泛函的解析刻画.本文设X是一个可分自反Banach空间,我们引入一个Banach空间值Bargmann-Segal空间E2(v,X),其中v是广义函数空间E*C上的复Gauss测度,并讨论Banach空间值广义泛函的解析刻画.
1 预备知识

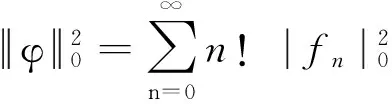
(A1)infspec(A)≥1.

记
这里D∞和D-∞是一列可分Hilbert空间的投影极限和归纳极限,在其上分别赋予投影极限拓扑和归纳极限拓扑.
除此之外,Dp(D∞)的对偶空间D*p(D*∞)与D-p(D-∞)同构.D-p×Dp(D*∞×D∞)上的典则双线性型表示为·,·,它在HC上与内积一致.由此我们得到一个Gelfand三元组:
通过二次量子化方法,得到一个新的Gelfand三元组:



显然,对∀Φ∈Gp,Φ的S变换能被唯一地扩张为D-p上的一个完全解析函数.
我们引入Bargmann-Segal空间.除了条件(A1)外,自伴算子A还满足下列条件:
(A2)A是一个实算子,即A(Dom(A∩H))⊂H;
(A3)存在一个嵌入D∞∩H中稠密且连续的实核空间E,使得E在A之下不变.
因此,E⊂D∞⊂H⊂D*∞⊂E*,E*×E上的典则双线性型表示为·,·.
设μ1/2是E*上的高斯测度,其特征函数为

由v(dz)=μ1/2(dx)μ1/2(dy)(z=x+iy,x,y∈E*)定义了E*C=E*+iE*上的一个概率测度v,v是复高斯测度,(E*C,v)是复高斯空间.
设P是定义在E*C上值域落在HC中的有限秩投影算子全体的集合,B⊂P可以很自然地从E*C扩张为HC上的一个连续算子.定义标量值Bargmann-Segal空间

定理A[8]设p,q∈R,D∞×D∞上的一个C值函数Ξ是广义算子T∈L[Gp,Gq]的象征的充要条件是:
(i)Ξ可以扩张为Dp×D-q上的解析函数;
(ii)存在一个常数λ≥0,使得对∀k≥1,ξj∈Dp,aj∈C,j=1,2,…,k,都有

定理B[9]设p∈R,D∞上的解析函数g是Φ的一个S变换,当且仅当g可以扩张为D-p上的一个连续函数,且g∘Ap∈E2(v).

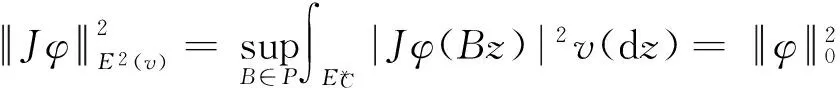
2 Banach空间值Bargmann-Segal空间和Banach空间值广义泛函的刻画
我们将引入Banach值Bargmann-Segal空间并且给出Banach空间值广义泛函的解析刻画.


(i)g是HC上的解析函数,即


定义2 定义在G∞(Gp,p∈R)上取值于Banach空间X的连续线性泛函称为Banach空间值广义泛函,其全体形成的空间记作L[G∞,X](L[Gp,X]).
命题1 设p∈R,T∈L[Gp,X],则对任意k≥1,aj∈C,fj∈X*,j=1,…,k,都有
(1)

证明 对f∈X*,有
于是对∀k≥1,fj∈X*,aj∈C,j=1,2,…,k,有

所以(1)式成立. 】
接下来应用Banach空间值Bargmann-Segal空间E2(v,X)讨论Banach空间值广义泛函L[G∞,X]或L[Gp,X],p∈R的解析刻画,同时给出广义泛函T∈L[Gp,X]的算子范数.


(ii)Ξ可以扩张到Dp上且Ξ∘A-p∈E2(v,X).

证明 因T∈L[Gp,X],所以∀f∈X*,T*f∈G-p,且对ξ,η∈D∞及ω∈C,有

由指数向量{ε(ξ):ξ∈Dp}的稠密性知,S(T*f)可以扩张到Dp上.

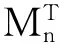

即Ξ∘A-p∈E2(v,X),且
反过来,X值函数Ξ满足一定条件时,可唯一确定一个向量值广义泛函T∈L[Gp,X].
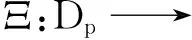

(ii)存在常数λ≥0,使得对∀k≥1,aj∈C,fj∈X*,j=1,2,…,k,有

证明 由( i )可知Ξ是解析函数,我们可以证明对∀ξ,η∈Dp,有
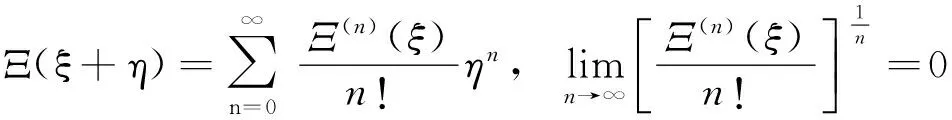
因此


(2)


所确定.又对∀f∈X*,ξ∈D∞,有
因此,

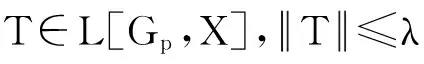
我们可以放宽对Ξ的条件,从而得到
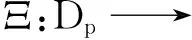

(ii)存在常数λ≥0,使得对∀k=1,aj∈C,fj∈N,j=1,…,k,有


定义Ff:Dp→C为Ff(z)=f,Ξ(z),则由定理2,我们可将证明补充完整. 】
推论1 设N是X*的完全子集,T∈L[Gp,X],如果存在一个常数λ≥0,使得对∀k≥1,aj∈C,fj∈N,j=1,…,k,有

证明 由定理3可知,对∀f∈X*,条件(ii)成立,且对φ∈Gp,Tφ∈X,有
因此,
[1] HIDA T,KUO H H,STREIT J P L.WhiteNoise:AnInfiniteDimensionalCalculus[M].Dordrecht:Kluwer Academic,1993.
[2] HUANG Z Y,YAN J A.IntroductiontoInfiniteDimensionalCalculus[M].Dordrecht:Kluwer,1997.
[3] KUO H H.WhiteNoiseDistributionTheory[M].Boca Raton:CRC Press,1996.
[4] OBATA N.WhiteNoiseCalculusandFockSpace[M].Berlin:Springer,1994.
[5] WANG C S.A new idea to define theδ-function of an observable in the context of white noise analysis,infinite dimensional analysis[J].QuantumProbabilityandRelatedTopics,2005,8(4):659.
[6] JI U C,OBATA N.A unified characterization theorem in white noise theory[J].InfinDimensAnalQuantumProbabRelatTop,2003,6:167.
[7] WANG C S,CHEN J S,QU M S.An analytic characterization of B-valued generalized functionals of white noise[J].ActaMathSinica,2007,27(A):322.
[8] GROTHAUS M,KONDRATIEV G Y,STREIT L.Complex gaussian analysis and the Bargmann-Segal space[J].MethodsFunctAnalTopology,1997,3:46.
[9] HIDA T.BrownianMotion,ApplicationsofMathematics[M].New York:Springer,1980.
[10] WANG C S,HUANG Z Y.A moment characterization of B-valued generlized functionals of white noise[J].ActaMathematicaSinica(English Series),2006,22(1):157.
[11] WANG C S,HUANG Z Y,WANG X J.Analytic characterization for Hilbert-Schmidt operators on Fock space[J].ActaMathematicaSinica(English Series),2005,21(4):787.
[12] HUANG Z Y.Quantum white noise-white noise approach to quantum stochastic caculus[J].NagoyaMathJ,1993,129:23.
(责任编辑 马宇鸿)
The characterization of Banach-valued generalized functional by Banach-valued Bargmann-Segal space
ZHOU Yu-lan,WANG Xuan-jing
(College of Mathematics and Information Science,Northwest Normal University,Lanzhou 730070,Gansu,China)
The Banach-valued Bargmann-Segal spaceE2(v,X) is introduced,wherevis complex Gauss measure in generalized functional spaceL[Gp,X],Xis a complex separable reflexive Banach space.The totality of exponential vectors set {ε(ξ):ξ∈Dp} is used to discuss the analytic characterization of Banach-valued generalized functional viaL[Gp,X],wherep∈R.Meanwhile,thegeneralizedoperatornormisgivenbymeansofHilbertoperatornormofgeneralizedfunctionalinE2(v,X).
whitenoiseanalysis;Banach-valuedBargmann-Segalspace;generalizedfunctional;analyticcharacterization
10.16783/j.cnki.nwnuz.2016.01.003
2015-09-15;修改稿收到日期:2015-10-09
国家自然科学基金资助项目(11461061)
周玉兰(1978—),女,甘肃天水人,副教授,博士.主要研究方向为随机分析及其应用.
E-mail:zhouylw123@163.com
O 177.2
A
1001-988Ⅹ(2016)01-0012-05

