无证书的层次认证密钥协商协议

苏航，刘建伟，陶芮

（北京航空航天大学电子信息工程学院，北京 100191）

无证书的层次认证密钥协商协议

苏航，刘建伟，陶芮

（北京航空航天大学电子信息工程学院，北京 100191）

提出了一种无证书的层次认证密钥协商协议，协议的安全性基于计算性Diffie-Hellman困难假设，并在eCK（extended Canetti-Krawczyk）模型下证明了该协议的安全性。该协议中，根PKG为多层的域PKG验证身份并生成部分私钥，域 PKG为用户验证身份并生成部分私钥，私钥则由用户选定的秘密值和部分私钥共同生成。与已有协议相比，协议不含双线性映射配对运算，且具有较高的效率。

无证书；层次认证密钥协商协议；计算性Diffie-Hellman困难假设；eCK模型

1 引言

密钥协商是保障节点间安全通信的重要机制。在传统公钥基础设施[1]（PKI, public key infrastructure）中，需要证书来验证用户的身份。因此，PKI中涉及大量的证书管理问题。为了简化这一问题，Shamir[2]于1984年提出基于身份的密码体制（IBC,ID based cryptography）。在该体制中，选取用户的身份作为公钥，私钥由可信的私钥生成中心 PKG生成。然而在IBC中，PKG可掌握所有用户的私钥，这就是IBC中固有的密钥托管问题。在2003年，Al-Riyami和Paterson[3]提出了无证书的公钥密码体制（CLPKC, certificateless public key cryptography），这一体制解决了 IBC中的密钥托管问题。利用CLPKC，学者们提出了大量的无证书认证密钥协商协议[4～10]。

在空间信息网络中[11]，含有多种异构网络和大量网络节点，集中式的管理模式会因数据流过于集中，而导致网络拥塞和服务延时及单点失效问题。空间节点的软硬件处理能力相对较低，处理资源和带宽相对较少，电源和推进能力有限。对于部分实时性要求较高的任务，通常不允许在运算过程中耗费过多时间。上述机制均是在单一 PKG环境下提出的，不适用于含有大量节点的空间信息网。Gentry等[12]提出了基于身份的层次加密体制（HIBC, hierarchical ID based cryptography），该体制中包含一个根PKG及多层的域PKG，根PKG对域PKG进行验证并为其生成私钥，上层域 PKG验证下层域PKG并为其生成私钥，直至用户的上一层域。利用HIBC体制，Cao等[13]和Liu等[14]分别提出了基于身份的层次认证密钥协商协议，不过这些协议没有解决 IBC固有的密钥托管问题。Chow、Roth和Rieffel[15]于 2008年首次对无证书的分层密码体制（HCLC, hierarchical certificateless cryptography）进行了研究。这一体制既保留了HIBC体制的优点，又避免了HIBC体制中的密钥托管问题。

本文基于HCLC体制，提出一种无证书的层次认证密钥协商协议，并在eCK模型下证明了其安全性。在本文协议中，多层 PKG有效防止了单点失效问题，减轻了 PKG的运行压力，提高了系统的承载能力，而且，解决了IBC体制中固有的密钥托管问题。协议的计算开销与双方用户所处层级呈线性关系，运算过程不含双线性对运算，具有较高的效率，适用于计算能力小的空间节点。

2 预备知识

2.1 椭圆曲线

y2且

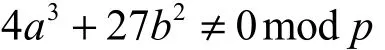
群G为循环加法群，群运算为加法运算（点乘运算），描述如下

2.2 困难问题及假设

计算性 Diffie-Hellman问题（CDH, computational Diffie-Hellman problem）：G为q阶的循环加法群，给定P, aP, bP∈G（ a, b ∈是未知的随机数），计算abP∈G。

定义1 多项式时间算法A在安全常数λ下解决CDH问题的优势定义如下

定义2 CDH假设指出，不存在多项式时间算法A，使其具有不可忽略的优势

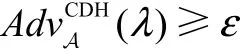
可以解决CDH问题。

2.3 无证书的层次密钥协商协议定义

结合无证书的密钥协商协议[4～10]及无证书的层次密码体制定义[15]，本节给出无证书的层次认证密钥协商协议的定义。

1) ( pp, m sk)←Root-Setup(λ)：系统建立算法Root-Setup以安全常数λ∈N作为输入，输出全局性系统参数pp及主私钥msk。

2) (k)← Partial-Private-Key-Extract(msk,ID)：部分私钥生成算法 Partial-Private-Key-Extract以主密钥 msk和任意一个用户身份向量 ID =(I1, I2,… ,It)作为输入，输出为该用户ID的部分私钥k。

3) (x)←Set-Secret-Value(pp, ID)：秘密值生成算法Set-Secret-Value以全局性系统参数pp和用户ID作为输入，输出为该用户ID的私有秘密值x。

4) (d)←Set-Private-Key(k, x)：私钥生成算法Set-Private-Key以部分私钥k和用户的私有秘密值x作为输入，输出为该用户ID的私钥d。

5) (pk)←Set-Public-Key(pp,x)：公钥生成算法Set-Public-Key以全局性系统参数pp和用户ID的私有秘密值x作为输入，输出为用户的公钥。

6) (k)← Partial-Delegate(k′,ID)：部分私钥委托算法Partial-Delegate以用户身份向量 ID′ =(I1,…,It−1)的部分私钥k′、用户身份向量 ID =(I1, I2,… , It)作为输入，输出为用户ID的部分私钥k。

7) (T)←Temporary(d)：临时信息生成算法Temporary以用户私钥d作为输入，输出为用于密钥协商阶段的临时信息T。

8) (sk)← Agreement(pk′, T′, d)：密钥协商算法Agreement以参与密钥协商的用户的私钥d和另一用户的公钥pk′及其临时信息T′作为输入，输出为协商的会话密钥sk。

2.4 安全模型

在无证书的密钥协商协议中存在2种类型的敌手[6]，其具有的攻击能力如下。

敌手1 敌手A1是一个不诚实的参与者，他不能获取系统的主私钥，但是可以任意替换参与密钥协商的用户的私有秘密值和公钥。

敌手2 敌手A2是一个恶意的PKG，但是不可以替换参与密钥协商用户的私有秘密值和公钥。

Lippold等[17]将传统的eCK模型扩展成无证书体制下的eCK模型。每个参与者被模拟为多项式时间图灵机，可以并行地执行多项式通信会话，称会话为参与者I和J的第s个会话。此模型是通过挑战者C和敌手A之间的游戏来定义的，游戏可分为2个阶段。

阶段1 A被允许以任意顺序做如下查询。

Creat(IDi)：C是身份为IDi的参与者生成公私钥对。称不被A控制的用户为诚实用户。

RevealMasterKey：C返回系统主私钥给A。

RevealPartialPrivateKey(IDi)：C返回IDi的部分私钥给A。

RevealSecretValue(IDi)：C返回IDi的私有秘密值给A。

ReplacePublicKey( IDi, pk)：C将IDi的私有秘密值和公钥替换为A选定的值。

RevealEphemeralKey( ∏s)：C返回ID的临时

I,Ji私钥给A。

一旦A认为第一阶段可以结束了，则选择一个新鲜会话开始第2阶段的游戏。

在游戏的最后，A需要输出一比特'{0,1}b∈ 。如果b′=b，则A赢得此次游戏。定义A赢得游戏的优势为

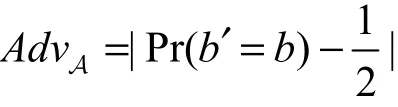
定义5 安全性。若一个无证书密钥协商协议满足下列条件。

2) A赢得游戏的优势AdvA是可以忽略的。那么本文称该协议在eCK模型下是安全的。

3 协议设计

3.1 协议描述

本文提出的无证书的层次认证密钥协商协议包 括 Root-Setup、Partial-Private-Key-Extract、Set-Secret-Value、Set-Private-Key、Set-Public-Key、Partial-Delegate、Temporary、Agreement这 8个部分，协议的具体构造过程如下。

1) (pp, msk)←Root-Setup(λ)：系统建立算法选取满足安全常数λ的阶为q的椭圆曲线循环加法群G，即|q|=λ，G的生成元为P。选取安全的散列函数G × G →K，其中，K为会话密钥空间。选取主私钥msk=s，计算公钥Ppub=sP。输出共享的全局性系统参数

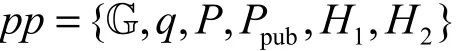
2) (k)← Partial-Private-Key-Extract (msk, ID)：给定主私钥 msk和任意一个用户身份向量ID =(,… ,It)，部分私钥生成算法随机选取计 算 r = H( I ||g P)， 其 中 ，

i1i i

1≤i≤t。输出该用户所对应的部分私钥

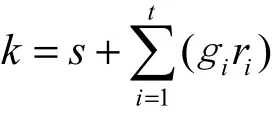
若等式不成立，则拒绝此部分私钥。

3) (x)←Set-Secret-Value(pp, ID)：给定全局性系统参数pp，秘密值生成算法随机选取 x∈Z*q，输出用户ID的私有秘密值为x。

4) (d)←Set-Private-Key(k, x)：给定用户ID的部分私钥k和私有秘密值x，输出该用户ID的私钥

若d=0，则需要重新执行Set-Secret-Value算法。

5) (pk)←Set-Public-Key( pp, x)：给定全局性系统参数pp和用户ID的私有秘密值x，输出该用户ID的公钥

6) (k)← Partial-Delegate(k′,ID)：部分私钥委托算法由用户 ID =(I1, I2,… ,It)的上层PKG运行，其中PKG的部分私钥为部分公钥为随机选取 gt∈，计算PKG为用户ID生成部分私钥

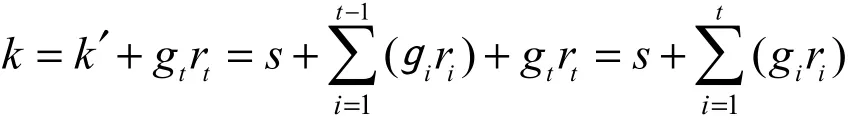
若k=0，则需要重新选取 gt∈。通过安全信道将{g1P, … , gtP, k }发送给用户 ID，其中，g1P,… , gtP为用户ID的部分公钥。用户验证等式为

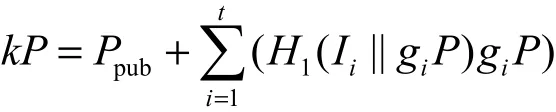
若等式不成立，则拒绝此部分私钥。若等式成立，用户可执行 Set-Secret-Value、Set-Private-Key和Set-Public-Key算法生成自己的私钥和公钥。

7) (T)←Temporary(d)：用户A和B分别执行临时信息生成算法，A随机选取临时私钥 tA∈，计算 TA=tAdAP，发送{pkA}给B。B随机选取临时私钥 tB∈，计算 TB=tBdBP，发送{TB,p kB}给A。

8) (sk)← Agreement(pk′, T′, d)：用户 A 和 B分别执行密钥协商算法，计算会话密钥。

A计算

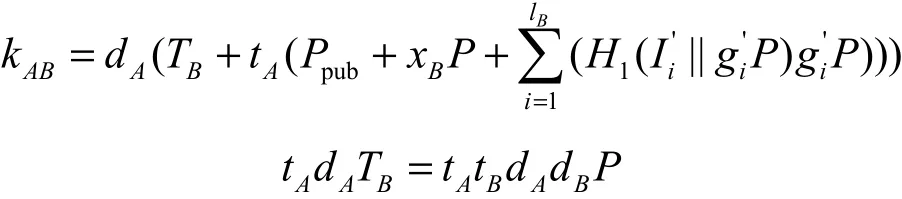
会话密钥

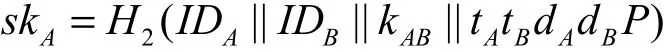
B计算

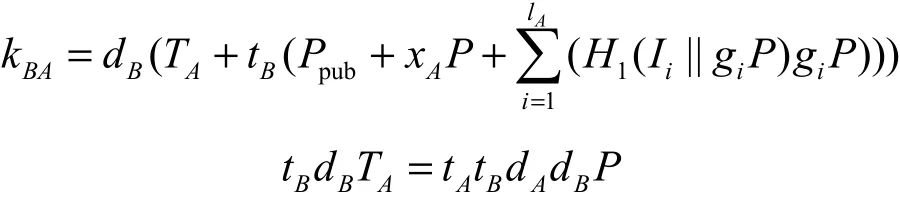
会话密钥

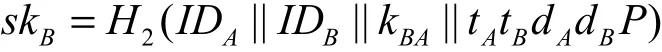
3.2 协议正确性

要证明协议中用户 A和 B获得相同的会话密钥，即 skA=skB，只需证明 kAB=kBA，证明如下。

用户A做如下计算

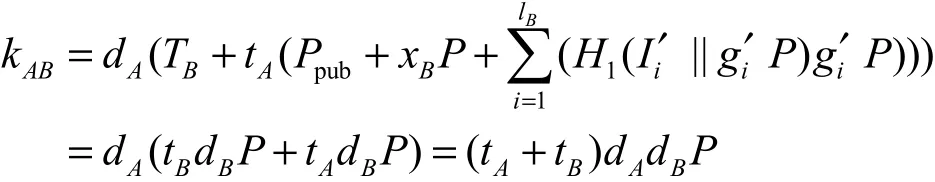
用户B做如下计算

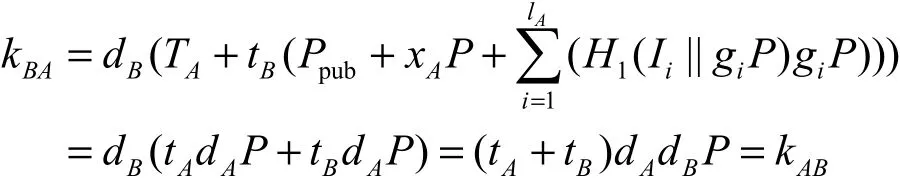
因此，用户A与用户B可计算获得相同的会话密钥。

4 安全性分析

本节在基于身份的eCK模型[7]下证明本文协议的安全性，在证明过程中将模拟根 PKG为不同层次的节点生成部分私钥的功能，密钥托管功能可由相同方式模拟。假定散列函数H1和H2是随机预言机，由定义可知匹配会话和可计算得到相同的会话密钥。

4.1 引理1的证明

引理1 假定CDH假设成立，则本文协议在A1的攻击下在eCK模型下是安全的。

证明 假设A1以不可忽略的优势 AdvA1在多项式时间内赢得在2.4节中定义的游戏，那么C可利用A1的能力解决CDH问题。C选择 s∈，并令 Ppub= P0= sP 。令全局系统参数 pp ={G,q, P, P0,H1, H2}，并发送pp给敌手A1。

令n0表示每个参与者最多发起的会话数，假定敌手A1最多激活n1个诚实用户，最多做n2次散列H2查询。当A1做Test查询后，只有3种方法来赢得此游戏。

1) 猜测攻击：A1直接猜测出会话密钥。

2) 密钥复制攻击：A1使Test会话的一个非匹配会话拥有和Test会话一样的会话密钥，通过查询该非匹配会话的会话密钥赢得游戏。

3) 伪造攻击：在某时刻，A1向C进行了值为(I||J||Z1||Z2)的H2查询。此时，A1计算出了正确的Z1和Z2值。

通过协议构造和2.4节中的定义可知，猜测攻击的优势可以忽略。而由于H2中的会话标识符包含了通信双发的身份及发送和接受的消息，非匹配会话不可能拥有与Test会话相同的会话密钥，密钥复制攻击的优势也可忽略。因此，只需考虑伪造攻击的情形。

令AdvC为C解决CDH问题的优势。给定CDH问 题 实 例 U = uP, V = vP，C的 任 务 是 计 算W =CDH( U, V )= uvP 。C模拟2.4节定义的游戏，对A1的查询做出以下回答。

2) 不存在诚实的用户拥有Test会话的匹配会话。

A可以通过 ReplacePublicKey查询获得参与者的私有秘密值x和公钥xP。此时可分为以下4种情形。

1)A1既不知道I的临时私钥，也不知道J的部分私钥

C对A1的查询做出以下回答。

Creat(IDi)：假设 IDi=(I1, I2,… ,Ili)，C维护初始为空的列表L，记录格式为 { ID ,k, R1,… ,Rli,

C

若IDi=J，C在LC列表中找形如的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为 IDj=(I1, I2,… ,Ilj),lj≤li。选 取 L 列 表 中 相 应 的 rn,Rn， 随 机 选 择

H

计算

1

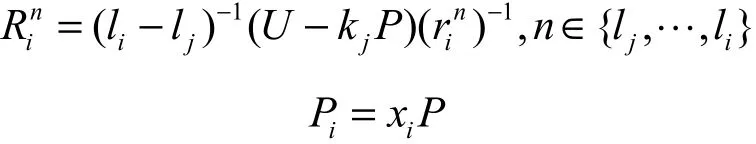
令 H( I ||Rn) = rn,n ∈ {1,… , l}，记录L元组为

1n i i iC记 录L 元 组 为H1

若 IDi≠ J, li=1，C随机选择计算

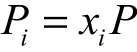
若 IDi≠ J, li≠1，C在LC列 表 中 找 形 如{ IDj,*,*,… , *,*,*}的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为选取 LH1列表中相应的随机选择 rlj,… ,rli,k, x∈Z*。计算i i i i q

H1( In,)查询：C维护初始为空的列表 LH1，记录格式为{ In,,}的元组。若(In,)在列表LH1中，则返回给A1；若不在，则随机选择∈返回给A1，并记录{ In,,}。

H2(I Di, I Dj,Z1, Z2)查询：C维护初始为空的列表LH2， 记 录 格 式 为{ IDi, I Dj,Ti, Tj, pki, pkj,Z1,Z2,s k}的元组。若 LH2中有记录则返回对应的sk给A1；若没有记录，则按如下操作。

若IDi=J，C在LS列表中找{ IDi, I Dj,Ti, Tj,pki, p kj, s k}的元组。若找到，则计算

若IDi≠J，C在LS列表中找的 元 组 。 若 找 到 ， 则 在 LH2中 记 录的元组，sk为LS中的值。否则，随机选取sk∈K，在 LH2中记录的元组。返回 sk给A1。

RevealSecretValue(IDi)：C查询LC列表，若找到形如{ IDi,*,*,… , *,*,*}的元组，则返回xi给A1；否则执行Creat(IDi)，再返回xi给A1。

ReplacePublicKey( IDi,pk)：C查询LC列表，若找到形如{ IDi,*,*,… , *,*,*}的元组，则替换 xi, Pi为A1所选值；否则执行Creat(IDi)，再替换 xi, Pi为A1所选值。

RevealPartialPrivateKey(IDi)：若IDi=J，则C停止模拟；否则，C发送部分私钥给A1。

若IDi=J，C随机选取并计算

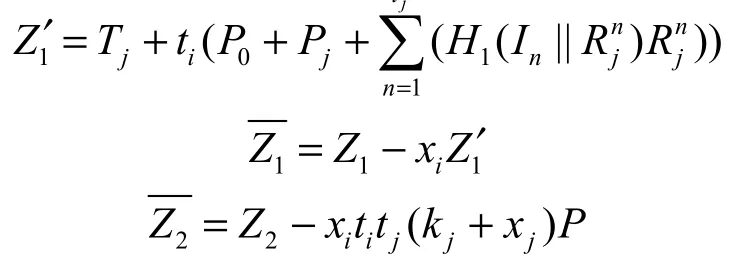
Test( ∏s)：若≠，则C停止模拟；否

I, J

则，C随机选取ξ∈K，发送ξ给A1。

假定A1赢得此次游戏，则A1必定计算出了正确的Z、Z。C则有的概率在 L 中找到对应

12H2

的正确元组。又因为 TI= tI( kI+ xI) P = V ，则

否则，按照协议规则进行回答。

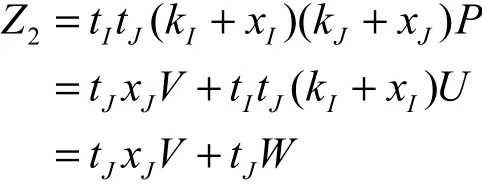
A1忽略，则AdvC也不可忽略。这与CDH假设矛盾。

2) A1既不知道 J的临时私钥，也不知道I的部分私钥

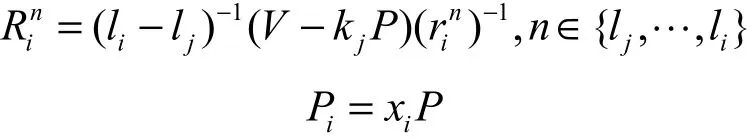
H2查询：C维护初始为空的列表LH2， 记 录 格 式 为Z2,s k}的元组。若 LH2中有记录则返回对应的sk给A1；若没有记录，则按如下操作。

若IDi=I或IDi=J，则按照1)中IDi=J时进行，其余按照1)中的规则进行。

RevealPartialPrivateKey(IDi)：若 IDi=I或IDi=J ，则C停止模拟；否则，C发送部分私钥给A1。

假定A1赢得此次游戏，则A1必定计算出了正确的Z、Z。C则有的概率在 L 中找到对应

12H2的正确元组，则

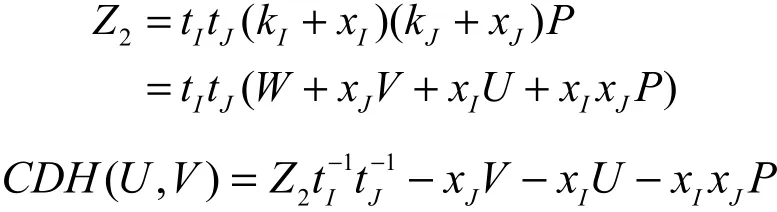
4) A1不知道I和J的临时私钥

除以下查询的回答不同外，其余查询均按照1)中的规则进行。

Creat(IDi)：假设 IDi=(I1, I2,… ,Ili)，C维护初始为空的列表LC，记录格式为的元组。C按如下规则生成元组数据。

C在LC列表中找形如的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为 IDj=(I1, I2,… ,Ilj),lj≤ li。选取LH1列表中相应的随 机 选 择计算

H2查询：C维护初始为空的列表LH2， 记 录 格 式 为Z2,s k}的元组。若 LH2中有记录则返回对应的sk给A1；若没有记录，则按如下操作。

C在LS列表中找的元组。若找到，则计算

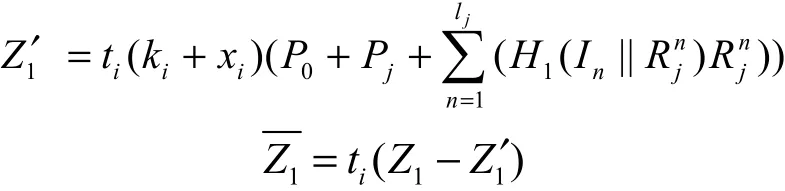
RevealPartialPrivateKey(IDi)：C查找LC列表，发送部分私钥给A1。

1i1按照协议规则进行回答。即可。

3) A1不知道I和J的部分私钥

除以下查询的回答不同外，其余查询均按照1)中的规则进行。

Creat(IDi)：假设 IDi=(I1, I2,… , Ili)，C维护初始为空的列表LC，记录格式为 { IDi,ki,,… ,,}的元组。C按如下规则生成元组数据。

若IDi=I，C在LC列表中找形如{ IDj,*,*,… ,*,*,*}的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为 IDj=(I1, I2,… ,Ilj),l≤l。选取 L 列表中相应,，随机选择

j iH1

假定A1赢得此次游戏，则A1必定计算出了正确的Z、Z。C则有的概率在 L 中找到对应

12H2的 正 确 元 组 。 又 因 为 TI= tI( kI+ xI) P = U ，TJ= tJ(kJ+ xJ)P = V ，则

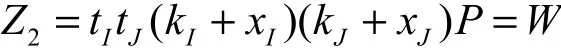
所以 CDH( U, V)=Z2。

4.1.2 不存在诚实的用户拥有Test会话的匹配会话

不存在诚实的用户拥有Test会话的匹配会话可分为以下2种情形。

1) A1拥有 I的部分私钥和私有秘密值，根据新鲜性定义，敌手不能查询I的临时私钥。

2) A1不知道 I的部分私钥和私有秘密值，根据新鲜性定义，敌手可以查询I的临时私钥。

上述2种情形分别与4.1.1节1）和2）类似，同理可证明其安全性。

4.2 引理2的证明

引理2 假定CDH假设成立，则本文协议在A2的攻击下在eCK模型下是安全的。

证明 假设A2以不可忽略的优势 AdvA2在多项式时间内赢得了在2.4节中定义的游戏，那么C可利用A2的能力解决CDH问题。同引理1中证明类似，此时本文只需考虑2种情形。

2) 不存在诚实的用户拥有Test会话的匹配会话。

A2作为恶意PKG可以获得所有参与者的部分私钥k。此时，存在诚实的用户拥有Test会话的匹配会话又可分为以下4种情形。

1) A2既不知道I的临时私钥，也不知道J的私有秘密值

C对A2的查询做出回答，除以下查询的回答不同外，其余查询均按照4.1.1节中1)的规则进行。

Creat(IDi)：假设 IDi=(I1, I2,… ,Ili)，C维护初始 为 空 的 列 表LC， 记 录 格 式 为 { IDi,ki,,… ,的元组。C按如下规则生成元组数据。

若IDi=J，C在LC列表中找形如*,… ,*,*,*}的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为 IDj=(I1, I2,… ,Ilj),l≤l。选取 L 列表中相应的,,，随机选

j iH1择计算

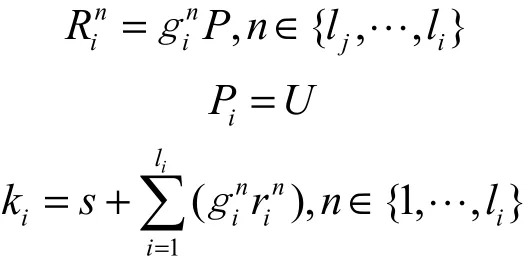
若IDi≠J，C在LC列表中找形如{I Dj,*,*,… ,*,*,*}的元组，其中，IDj为IDi的上层用户，取其中层级最大的用户，记为 IDj=(I1, I2,… ,Ilj),lj≤li。 若 li≠ 1， 则 选 取 LH1列 表 中 相 应 的随 机选择若 li=1，则 lj= 0，随机选择计算

C记 录 LH1元 组 为{In,Rin,

H2查询：C维护初始为空的列表LH2，记录格式为的元组。若 LH2中有记录则返回对应的 sk给A2；若没有记录，则按如下操作。

若IDi=J，C在LS列表中找的元组。若找到，则计算

LH2中记录的元组。返回sk给A2。

若IDi≠J，按4.1.1节中1)的规则回答。

RevealSecretValue(IDi)：C按以下规则回答。

若IDi=J，则C停止模拟；否则，按4.1.1节中1)的规则回答。

RevealPartialPrivateKey(IDi)：C发送部分私钥给A2。

RevealMasterKey：C返回主私钥给A2。

Send(∏s,m )：若=，则返回 T=V给

I,Ji

A2。若IDi=J，C随机选取*iqt∈Z，并计算

否则，按照协议规则进行回答。

假定A2赢得此次游戏，则A2必定计算出了正确的Z、Z。C则有的概率在 L 中找到对应

12H2的正确元组。又因为 TI= tI( kI+ xI) P = V ，则

剩余情形的证明与引理1类似，同理可得引理2成立。

由引理1和引理2可得出定理1。

定理1 本文基于CDH假设的协议在eCK模型下是安全的。

5 效率分析

5.1 协议复杂度

本节对本文协议主要算法的计算复杂度进行分析，并与文献[13,14]协议相对比，结果如表1所示。由于3种协议在构造上存在差别，所以分别以Key-Extract、Delegate和Agreement代表 3种协议的私钥生成、私钥委托和密钥协商算法。在分析计算复杂度时，主要考虑的计算类型有：椭圆曲线上的双线性对运算、循环加法群G中点乘运算及双线性群GT中的指数运算及散列函数运算。用 P表示双线性对运算，M表示点乘运算，E表示GT中的指数运算，H表示散列函数 H ：{0,1}*→G的运算。对于有系统最大层级限制的方案，用L表示系统最大层级，l表示用户所处层级，lA、lB为用户 A和 B的层级，i表示为用户A和B在第i层有相同的节点。

表1 计算复杂度分析

5.2 算法执行耗时

为了对比协议的计算开销，本节选取jpbc库中A类椭圆曲线进行测试，其曲线方程为 y2=x3+x，G群阶数为512 bit，域阶数为160 bit。测试平台的相关配置信息如表2所示。

本节对A类曲线中的双线性对运算、G群点乘运算、G群乘法运算、GT群指数运算、GT群乘法运算、域乘法运算、域加法运算及散列函数运算的单次运算耗时分别进行了测试，结果如表3所示。

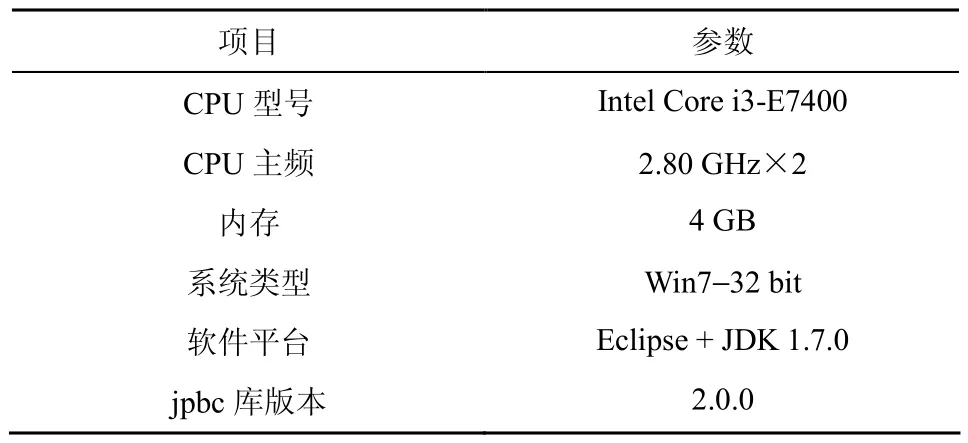
表2 测试平台配置

表3 单次运算执行耗时

假设系统层级为 7，表 4和表 5分别为Key-Extract和 Delegate算法的执行耗时。在Agreement算法中，本节选取3种情形进行测试，假设用户所处层级分别为 lA= 2、 lB= 7、i=1，测试结果如表6所示。

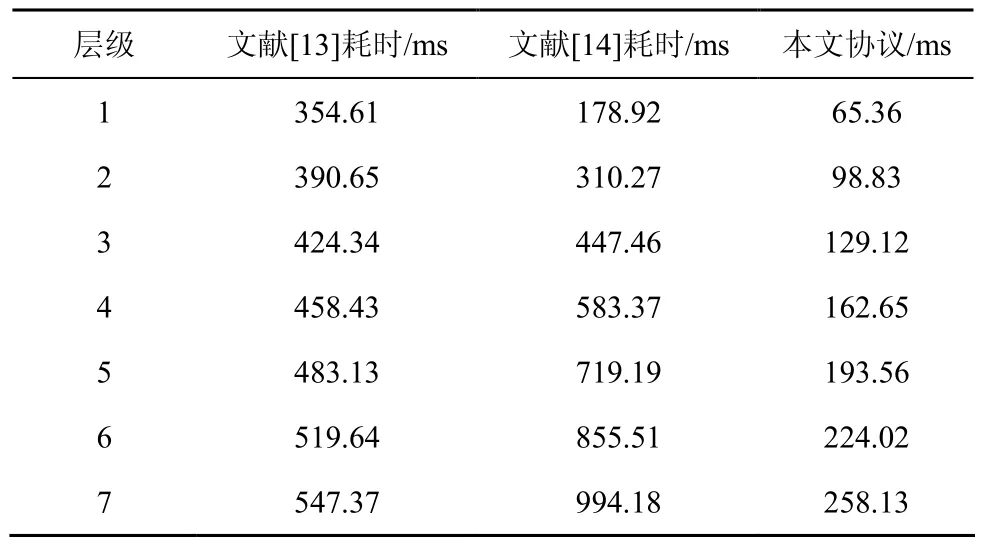
表4 Key-Extract算法执行耗时

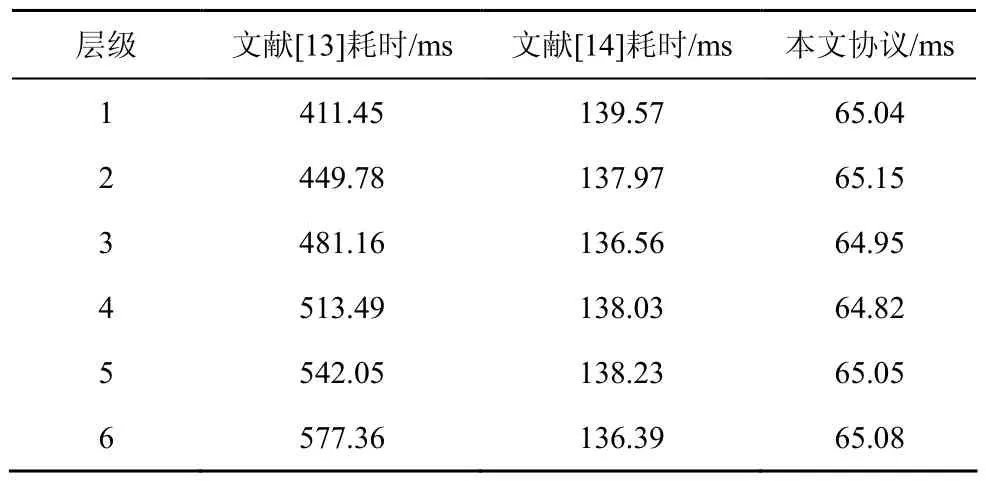
表5 Delegate算法执行耗时

表6 Agreement算法执行耗时

测试结果表明，与同类协议相比，本文协议不仅解决了身份基密码体制固有的密钥托管问题，而且具有较高的执行效率。在私钥生成和私钥委托算法方面，本文协议具有不可比拟的优势。在密钥协商阶段，算法耗时与用户所处层级之和呈线性关系。虽然算法耗时随着用户所处层级之和的增加而不断增加，但与前2种协议相比，本文协议仍具有较高的效率。

6 结束语

本文提出一种适用于空间信息网的无证书的层次认证密钥协商协议，并对协议的安全性进行了证明。本文协议不仅解决了传统公钥基础设施中的证书管理问题，而且避免了基于身份密码体制固有的密钥托管问题。与同类协议相比，本文协议具有较高的执行效率。本文协议对系统层级深度没有限制，扩大了无证书的层次认证密钥协商协议的适用范围。

[1] HUNT R. PKI and digital certification infrastructure[C]// Ninth IEEE International Conference on Networks. IEEE, c2001： 234-239.

[2] SHAMIR A. Identity based cryptosystems and signature schemes[C]//Advances in Cryptology Crypto84. Berlin： Springer-Verlag, c1984： 47-53.

[3] AL-RIYAMI S S, PATERSON K G. Certificateless public key cryptography[M]. Advances in Cryptology-ASIACRYPT 2003, Springer Berlin Heidelberg, 2003： 452-473.

[4] HE D, CHEN Y, CHEN J, et al. A new two-round certificateless authenticated key agreement protocol without bilinear pairings [J].Mathematical and Computer Modelling, 2011, 54(11)： 3143-3152.

[5] HE D, CHEN J, HU J. A pairing-free certificateless authenticated key agreement protocol[J]. International Journal of Communication Systems, 2012, 25(2)： 221-230.

[6] HE D, PADHYE S, CHEN J. An efficient certificateless two-party authenticated key agreement protocol[J]. Computers & Mathematics with Applications, 2012, 64(6)： 1914-1926.

[7] TONG D, LIU J W, MAO K F, et al. Certificateless and pairing-free key agreement scheme for satellite network[C]//Communications Security Conference (CSC 2014). IET, c2014： 1-5.

[8] MOHAMED N A F, HASHIM M H A, BASHIER E, et al.Fully-secure and efficient pairing-free certificateless authenticated key agreement protocol[C]// 2012 World Congress on Internet Security(WorldCIS), IEEE, c2012： 167-172.

[9] SUN H Y, WEN Q Y, ZHANG H, et al. A strongly secure pairing-free certificateless authenticated key agreement protocol for low-power de-vices[J]. Information Technology and Control, 2013, 42(2)： 191-204.

[10] GHOREISHI S M, ABD R S, ISNIN I F, et al. New secure identity-based and certificateless authenticated key agreement protocols without pairings[C]// 2014 International Symposium on Biometrics and Security Technologies (ISBAST). IEEE, c2014： 188-192

[11] WANG Z, DU X, SUN Y. Group key management scheme based on proxy re-cryptography for near-space network[C]// 2011 International Conference on Network Computing and Information Security (NCIS).IEEE. c2011, 1： 52-56.

[12] GENTRY C, SILVERBERG A. Hierarchical ID-based cryptography[M]. Advances in cryptology—ASIACRYPT2002, Springer Berlin Heidelberg, 2002： 548-566

[13] 曹晨磊, 刘明奇, 张茹, 等. 基于层级化身份的可证明安全的认证密钥协商协议[J]. 电子与信息学报, 2014, 36(12)： 2848-2854.CAO C L, LIU M Q, ZHANG R, et al. Provably secure authenticated key agreement protocol based on hierarchical identity[J]. Journal of Electronics & Information Technology, 2014, 36(12)：2848-2854.

[14] LIU W, LIU J, WU Q, et al. SAKE： scalable authenticated key exchange for mobile e-health networks[J/OL]. Security and Communication Networks, http：//onlinelibrary.wiley.com/doi/10.1002/sec.1198/epdf.

[15] CHOW S S M, ROTH V, RIEFFEL E G. General certificateless encryption and timed-release encryption [M]. Security and Cryptography for Networks, Springer Berlin Heidelberg, 2008： 126-143.

[16] HANKERSON D, VANSTONE S, MENEZES A J. Guide to elliptic curve cryptography [M]. Springer Science & Business Media, 2004.

[17] LIPPOLD G, BOYD C, NIETO J G. Strongly secure certificateless key agreement[M]. Pairing-Based Cryptography-Pairing 2009, Springer Berlin Heidelberg, 2009： 206-230.

Hierarchical certificateless authenticated key agreement protocol

SU Hang, LIU Jian-wei, TAO Rui
(School of Electronic and Information Engineering, Beihang University, Beijing 100191, China)

A hierarchical certificateless authenticated key agreement protocol was proposed, and the proposed protocol was proved secure in extended Canetti-Krawczyk (eCK) model, the security of the protocol was based on the computational Diffie-Hellman assumption. In the protocol, a root PKG authenticates the identity and generates a partial private key for lower-level PKG which authenticate the identity and generate a partial private key for users, private key generated by partial private key and user selected secret value. Comparing with the existing protocols, the protocol is efficient without bilinear pairings computation.

certificateless, hierarchical authenticated key agreement protocol, computational Diffie-Hellman assumption,eCK model

s: The National Basic Research Program of China (973 Program) (No.2012CB315905), The National Natural Science Foundation of China (No.61272501), The Fundamental Research Funds for the Central Universities (No.YWF-15-GJSYS-059)

ΤΝ918.1

A

10.11959/j.issn.1000-436x.2016145

2015-11-04；

2016-01-20

国家重点基础研究发展计划（“973”计划）基金资助项目（No.2012CB315905）；国家自然科学基金资助项目（No.61272501）；中央高校基本科研业务费专项基金资助项目（No.YWF-15-GJSYS-059）

苏航（1992-），男，安徽宿州人，北京航空航天大学硕士生，主要研究方向为空间网络安全、密码学。

刘建伟（1964-），男，山东莱州人，博士，北京航空航天大学教授、博士生导师，主要研究方向为密码学、网络与信息安全。

陶芮（1991-），女，天津人，北京航空航天大学硕士生，主要研究方向为密码学、网络与信息安全。