基于二级混沌映射的OFDM安全传输方案

王颖，张晓忠,2，曾娟,2，汪永明

(1. 中国科学院信息工程研究所，北京 100093；2. 中国科学院大学，北京 100049)

基于二级混沌映射的OFDM安全传输方案

王颖1，张晓忠1,2，曾娟1,2，汪永明1

(1. 中国科学院信息工程研究所，北京 100093；2. 中国科学院大学，北京 100049)

基于 OFDM 技术，结合混沌序列的伪随机特性和初值敏感性，提出了一种数据相位混沌旋转和子载波混沌映射的安全传输方案。仿真结果和分析表明，该方案能够有效地对信息进行混沌安全传输，增强输出信号的随机特性，窃听方无法通过信号的统计特性估计出发送信息，从而保证通信的安全性。与常用的安全措施，如AES（高级加密标准）、多天线随机化传输矩阵等方法相比，所述方案能够达到较好的计算安全性。

安全通信；混沌映射；OFDM；相位旋转；子载波映射

1 引言

20世纪40年代末，Shannon发表了密码学的奠基性论文《保密系统的通信理论》[1,2]，提出将混沌理论所具有的混合、对参数和初值的敏感性等基本特性，应用在密码学中，并提出了指导密码设计的2个基本原则：扩散和混乱。

传统的密码算法依赖于密钥的传递和提取，而混沌伪随机映射依赖于初始参数；传统的加密算法，通过增加加密轮次实现混乱和扩散，混沌理论通过迭代将初始域扩散到整个相空间。

以密码学为基础的加密技术，其核心在于不断提高密码破解的计算量，缺点在于加密过程主要针对网络层、应用层等高层协议，通信的底层基础不牢固，容易遭受DoS（拒绝服务）等攻击。

混沌理论应用在数字密码系统中，包含基于混沌伪随机数发生器的序列密码、基于前向混沌迭代/反向混沌迭代的分组密码（已有学者用选择密文攻击和已知明文攻击的方法破解了某些分组密码方案）以及散列函数的S盒设计等[3]。

混沌序列是由非线性动态系统产生的一种伪随机的非周期序列。当系统初值和参数一定时，所产生的混沌序列是确定的。混沌序列的产生过程是不收敛的、有界的，对初值及系数有极强的敏感性，导致混沌序列虽然具有确定性，但又是不可预测的[4]。由于具备如此良好的密码学特征，混沌序列已被广泛地应用于密码构建、图像加密和安全通信等领域[5,6]。

OFDM 技术具有频谱利用率高、带宽扩展性强、有效对抗多径衰落、实现简单、易于与多天线技术结合等优点。20世纪90年代，OFDM技术被广泛地应用在数字音/视频广播、无线局域网、超宽带等宽带数据通信系统中[7]。随着OFDM技术被广泛应用，其安全性也被广泛关注。

结合混沌理论的混沌安全通信技术，能够利用混沌系统的基本特性，有效提升OFDM系统的可靠性和安全性。Muhammad等[8]提出了一种基于符号混沌重排序的 OFDM 安全传输方案。Liu等[9]和Zhang等[10]提出了一种基于混沌加扰的时频域二维置换的物理层安全传输方案，分别应用于OFDM-PON（无源光网络）系统和CO-OFDM（相干光正交频分复用）系统，能有效地阻止外界非法者的恶意攻击。文献[11]提出了一种基于混沌序列和反向迭代的物理层混沌调制方案。

本文结合混沌序列的优良特性与 OFDM 系统中的调制和传输特性，从实用性和计算复杂度角度，提出了一种基于混沌序列的数据相位混沌旋转和子载波混沌映射的安全传输方案。

在OFDM系统的发射端基带信号处理中，随机改变星座图映射的相位，以及随机干预OFDM符号对子载波的映射选择，并将混沌映射的初始参数作为密钥，在信号接收端，能够按照该密钥产生的逆过程恢复出原始信号。即便信号在无线信道传输过程中被截获，截获方也无法根据“加密“信号得到真实信息。

2 Logistic混沌映射及分段Logistic映射

Logistic混沌映射是一种被广泛研究的混沌映射，其具有表达式比较简单、随机特性良好等特点。Logistic混沌映射的定义为

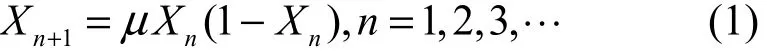
其中，0＜Xn＜1，1 ≤ µ≤ 4，µ称为分形参数。当3.569 94…≤µ≤4时，系统工作于混沌状态。Xn随机分布于0～1，是非周期、不收敛的序列，µ取值越靠近 4，这种随机性就越好。当µ的取值在此范围之外时，经过一定次数的迭代，Logistic映射必将收敛于一个固定数值，系统不能工作于混沌状态。

以下采用2种方法验证Logistic混沌映射的随机性能，第一种针对量化后的混沌序列，首先把混沌序列Xn转化成为二值序列An，其中，An∈{0,1}，转化公式如下

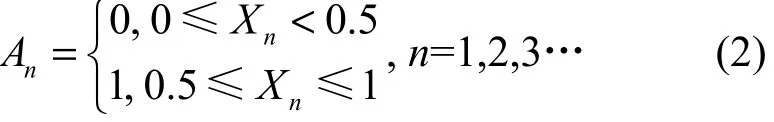
平衡性是衡量映射生成序列分布均匀和随机的一个标准，平衡性高的序列应该具有相同数目的0和1。假设混沌序列的长度为N，即转化而成的二值序列An长度为 N，设An中 0和 1的元素个数分别为J和K，则二值序列An的平衡度定义为[12]

图1为当µ=4，N=10 000，给定不同初值X0时，二值序列An的平衡度测试结果。结果显示，给定不同的X0，平衡度测试结果均接近于0，说明An中0和1的个数几乎相等，Logistic映射的随机性良好。

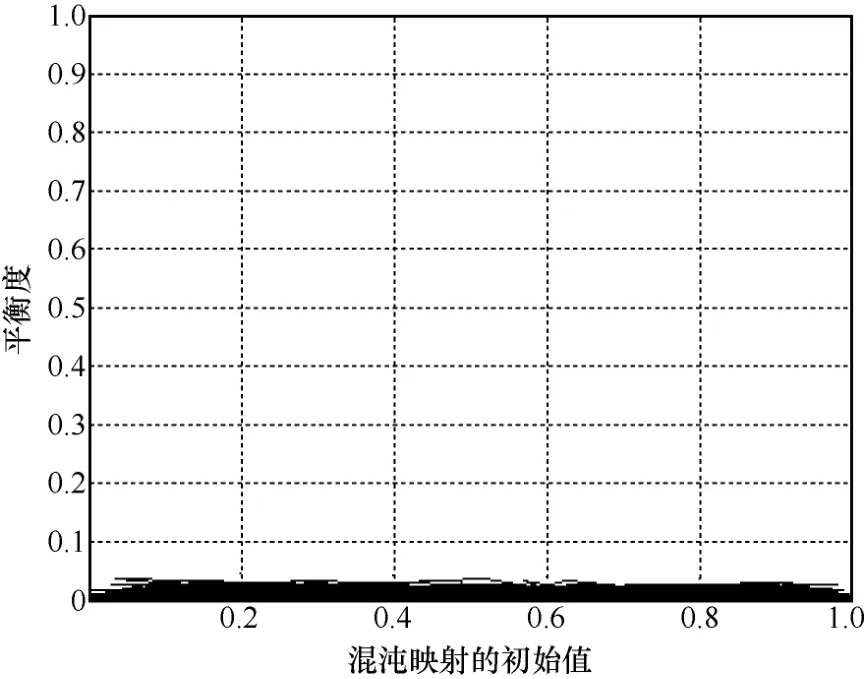
图1 Logistic混沌映射的平衡度

另一种验证Logistic映射随机性的方法，针对没有量化的混沌实值序列。根据定义产生一个长度为N=100 000的Logistic实值混沌序列，其中，每个值都是[0, 1]实数。如果对于[0, 1]中的任何数X，小于X的数占总数N的比例为X，那么可以说这个混沌序列的随机性较好。

图2为没有进行量化和预迭代处理的Logistic映射的随机性实验结果，没有进行预迭代的Logistic映射产生的实值序列的随机性与理想情况有一定差距。但是应用在OFDM系统中，经过二进制量化后的平衡度已符合预期目标，后续根据实际需求可以再做适应性的优化设计。

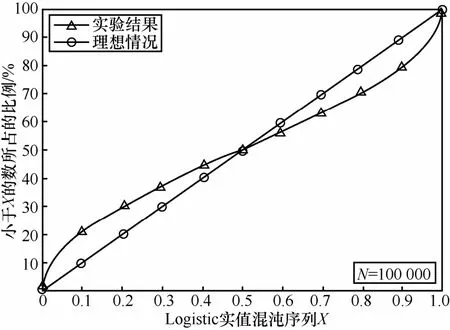
图2 Logistic混沌实值序列的随机性实验结果

文献[13]提出了一种分段 Logistic混沌映射，映射定义为

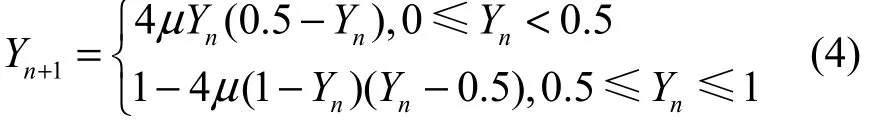
其中，3.569 94…≤µ≤4，0＜Yn＜1。实验证明，分段Logistic混沌映射和Logistic 混沌映射各方面性能相当，且其相邻轨道分离得更快，运动轨迹相比于Logistic 混沌映射更加不稳定。

本文以Logistic 混沌映射和分段Logistic 混沌映射为例进行说明，并分别产生OFDM系统的相位旋转因子序列和子载波映射因子序列，需要说明的是，所述方案可使用的混沌映射并不局限于Logistic映射。

3 OFDM混沌安全通信系统模型

OFDM混沌安全通信系统的系统模型，如图3所示，在传统OFDM系统的基础上，其数据发射端增加了相位混沌旋转模块和子载波混沌映射模块，分别对应了密钥K1、K2，信号经过无线信道传输后，利用密钥K1、K2在数据接收端恢复出传递的原始信号。以下讨论假设采用的数字调制方式为QPSK（四相相移键控）映射。

设 An为原始基带信号经过信道编码的输出序列，长度为N，Bn为An经过QPSK映射得到的复值信号，Bn共有 4 种状态{-1-i，-1+i，1-i，1+i}。相位旋转因子由Logistic混沌映射产生，其使用的分形参数µ、初始值X0，以及预迭代次数共同构成密钥K1。

为提高混沌映射的伪随机性和初值敏感性，方案中对映射序列采用了30次的预迭代，迭代次数取自多次实验得到的最优结果。需要注意的是，发送端和合法接收端需进行相同次数的预迭代处理才能恢复出原始的相位信息和载波位置信息。

首先，由混沌映射产生长度为mN(m=lbN)的混沌序列，由混沌序列生成的二值序列中每连续m位生成旋转因子序列 Wn，序列长度为 N，其中，W ∈ [0,2m− 1]。Wn中的元素即为Bn中对应数据的

n相位旋转因子。相位旋转引起的状态转化关系由下式给出，相位旋转后输出的序列用Cn表示为

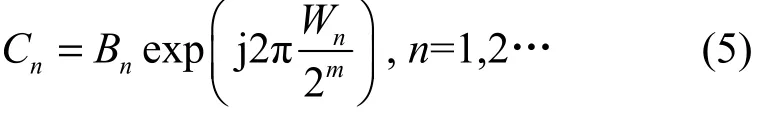
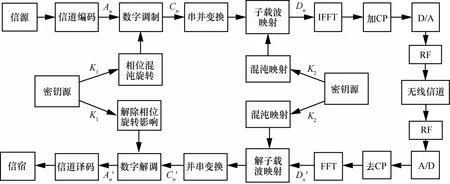
图3 OFDM混沌安全传输系统原理

当m=8和m=5的星座图对比情况如图4所示。随着 m的增大，相位旋转后的星座图呈现一个圆形，当m足够大，数据量足够多时，旋转后的星座图必将模糊成一个闭合的圆形，造成相位模糊，达到数据安全传输的目的。相位混沌旋转方法适用于所有的PSK调制情况，并可以推广到所有的QAM（正交幅度调制）数字调制系统。

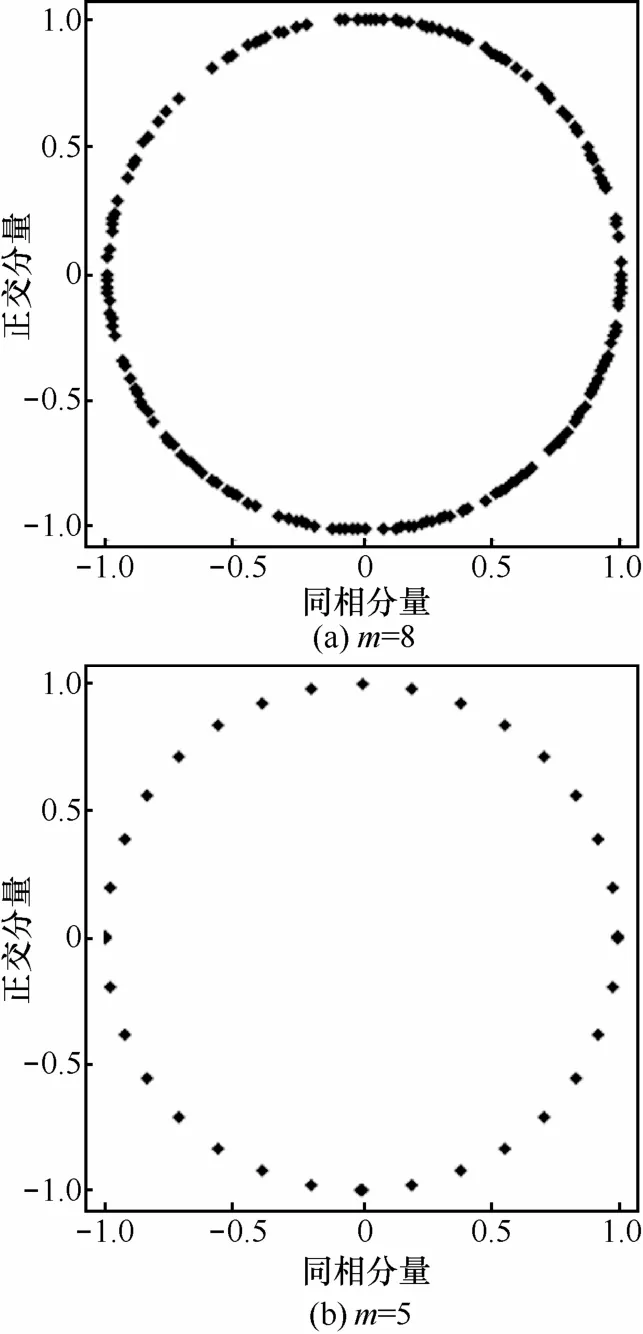
图4 不同m下相位旋转后星座图对比

上述相位混沌映射为第一重安全传输措施，下面介绍第二重安全传输措施，即子载波混沌映射。采用不同于相位混沌旋转时使用的混沌映射，即分段的Logistic混沌映射。混沌系统中使用的系统参数、初始值及预迭代次数构成密钥K2。

假设子载波个数为 N，混沌序列长度为mP(m=lbN，P>>N)，相位旋转输出的符号序列Cn在映射到子载波前，利用混沌序列产生二值序列，在此二值序列的控制下随机打乱子载波的映射位置。

量化后的混沌序列，其每 m位构成一个固定窗，用来产生子载波选择因子，由于混沌序列具有良好的遍历性[11]，子载波选择因子最终能够遍历0到N-1，组成子载波映射序列Vn，扰乱后的信息序列Dn为

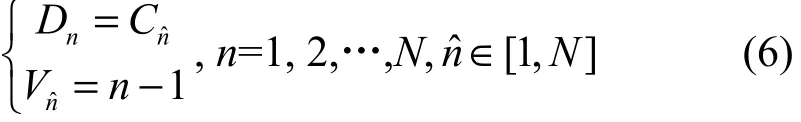
其中，ˆn表示经过混沌映射后新的子载波序号，n表示原始的从1到N的子载波序号，下同。实际应用时，实现的算法逻辑是在每一个0到N-1的整数产生时，需要与已保存在寄存器中的数进行比较，一旦出现重复的数值，即丢掉该数值，再用下一个m位二进制数重新产生，直至不重复，最后遍历0到N-1。

将扰乱顺序的信息序列 Dn调制到相应的载波位置上，送入信道传输，便能起到信息安全传输的目的。得到的OFDM信号的基带表述为

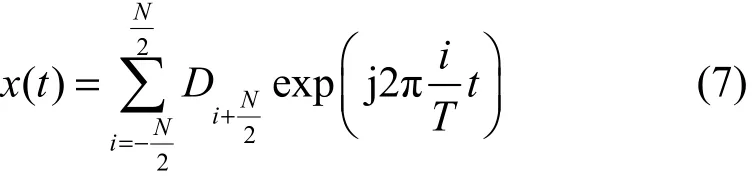
系统将密钥K1、K2通过隐蔽信道传递给合法接收端，接收机根据K1、K2还原出旋转因子序列和子载波映射序列，再根据该序列对“加密”信号进行解密。

为方便描述，假设信道模型为加性高斯白噪声信道，则接收端接收的信号可以表示为

其中，n(t)表示加性高斯白噪声。接收机利用子载波的正交特性，可以采用单路子载波信号进行解调，从而得到该路的数据。不考虑信道干扰和噪声的影响，以对第k路子载波进行解调为例，可以得到

分别对N路子载波进行解调，便可得到解调输出序列，记为Dn′。若信道模型为多径衰落信道，则会引入符号间干扰，上述解调方法不能正确解调出原始信号。为消除多径衰落的影响，需先对接收信号进行频域均衡，如ZF（迫零均衡）、MMSE（最小均方误差均衡）等，然后再解调数据。

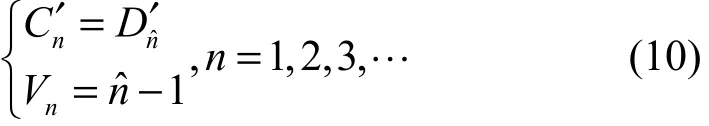
根据子载波映射序列对Dn′进行子载波逆映射再根据密钥K1恢复的旋转因子序列，解除相位混沌旋转的影响，如式(11)所示，对An′进行常规解调，即可恢复出原始信号。.

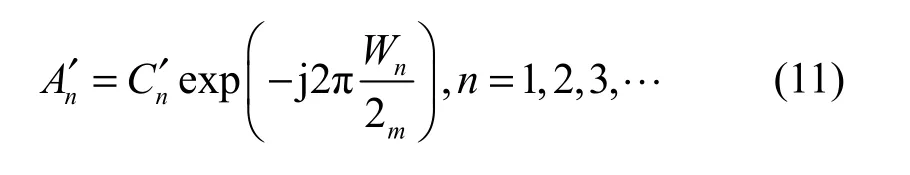
此过程中，经过QPSK调制后的信号Bn、相位混沌旋转后的信号Cn及子载波映射后的信号Dn的实部包络如图5所示。经过混沌映射模块传输后，信号波形的包络呈现出良好的随机特性。

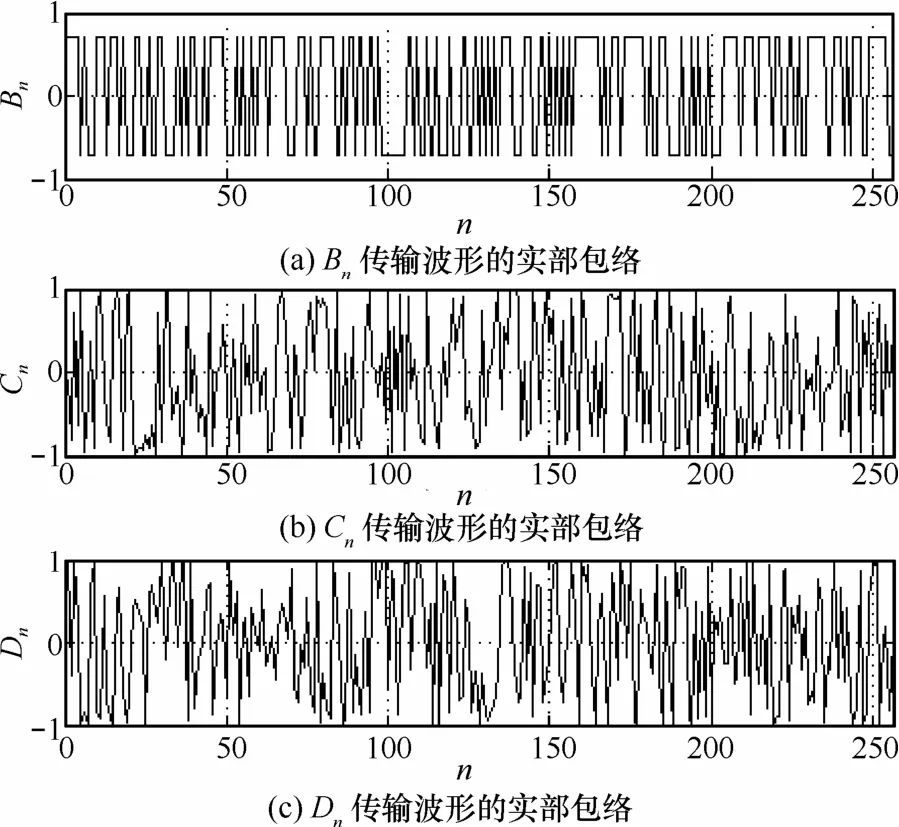
图5 Bn、Cn和Dn传输波形的实部包络

4 数值仿真

4.1 观测到的无线信号波形

系统设置和仿真参数，如表1所示。图6中对比了使用所述安全传输方案输出的时域信号波形与未使用混沌安全传输情况下得到的时域波形。从图6可以直观看出，2种情况下，时域波形的实部包络及虚部包络呈现出随机差异，所述方案对传输的数据具有随机“加密”的效果。

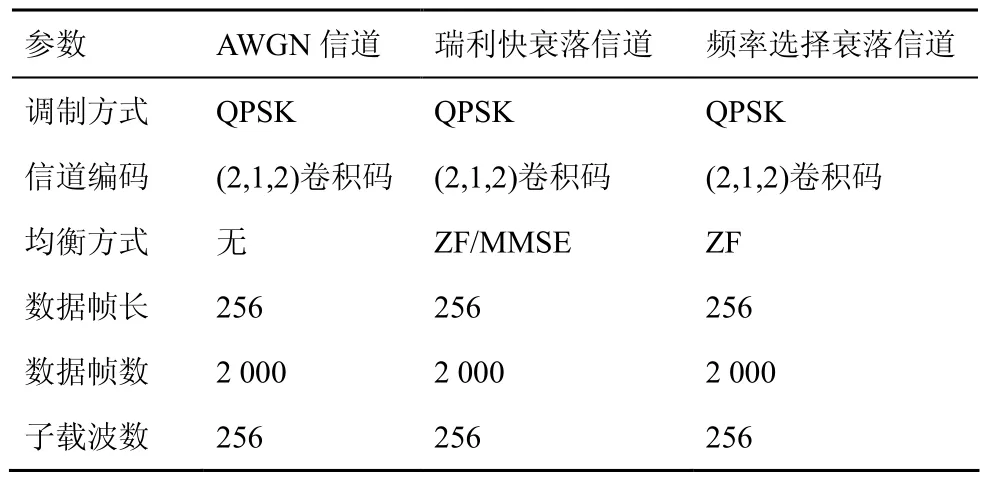
表1 仿真参数

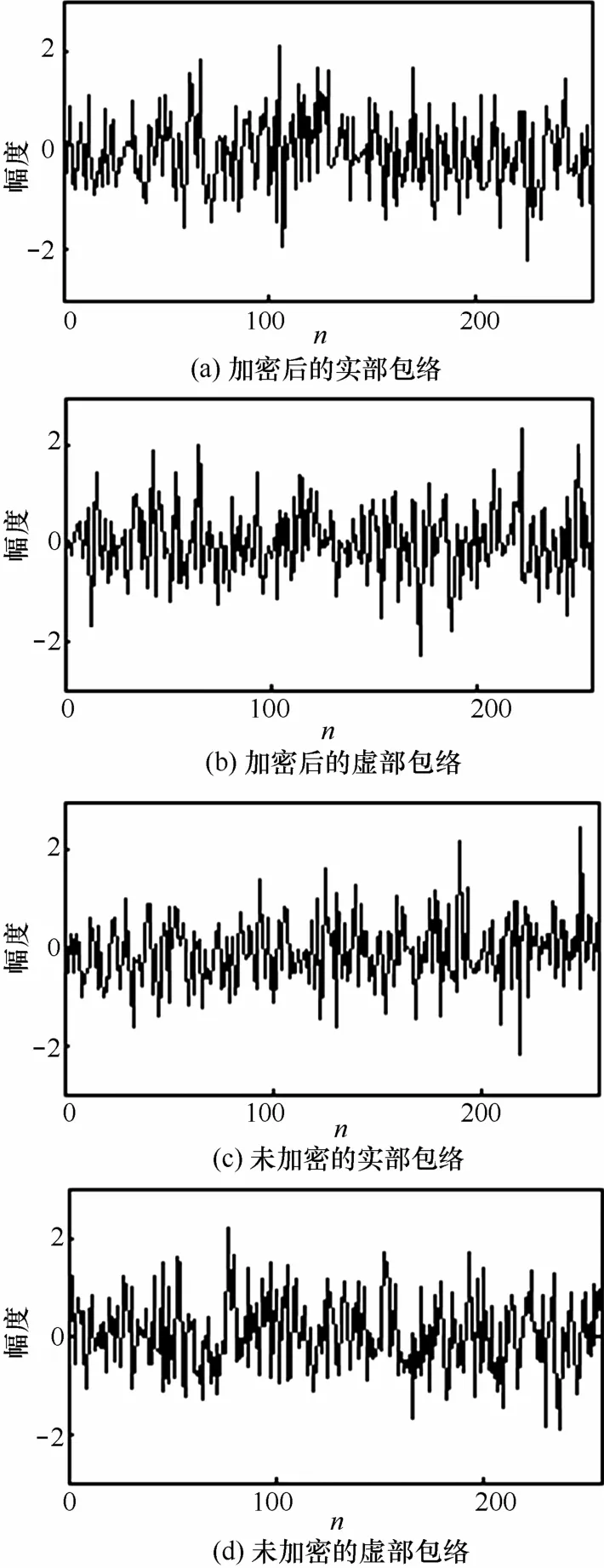
图6 采用安全传输措施前后信道时域波形对比

图7(a)和图7(b)描述的是采用QPSK调制，接收信噪比为10 dB时的解调星座图，图7(c)和图7(d)描述的是系统采用 16QAM调制，接收信噪比为15 dB时合法接收端和非法接收方的解调星座图，可以看出，非法接收方接收到的数据相位异常模糊，在不知传输密钥的情况下，无法正确解调出数据。

4.2 密钥空间与破译时间

混沌序列具有良好的初值敏感性和系数敏感性，实验表明，当初值或系数发生数量级为10-10的微小变动时，其相邻轨道发生完全分离的迭代次数约为30～35次。因而，假设混沌系统能够保持初值 X0和系数 µ敏感性的数量级为 10-10，本文提出的系统经过双重混沌安全传输后，密钥组合个数为 1.8×1039。

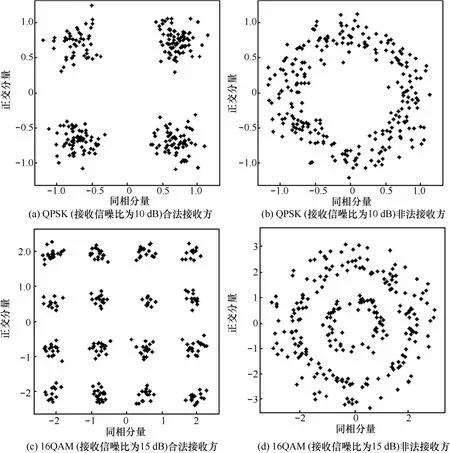
图7 合法接收方和非法接收方的数据星座

假设混沌映射能够一次性遍历0到N-1，非法接收方窃取传输数据后，最坏情况下所需的破译计算量为mN2lbN×1.8×1039。在每毫秒106次计算的速度下破解该方案所需要的时间是 mN2lbN×5.7×1022年。当m=8，N=256时，破解时间为2.4×1029年。

文献[14]比较了常用的加密措施，如射频指纹、采用AES算法的CDMA系统等，其密钥数及破解需要的时间，本文提出的安全传输方案与这几种方法的对比如表2所示。假设计算速度均为每毫秒106次。

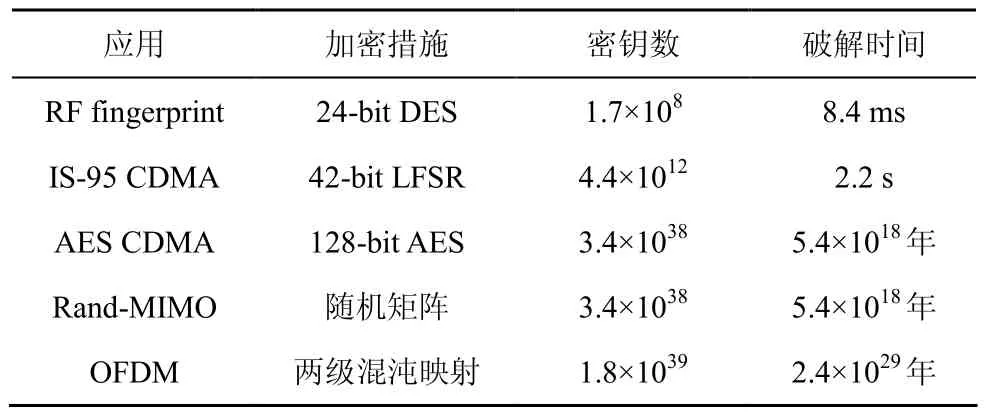
表2 不同加密措施的密钥数与破译时间对比

4.3 系统的通信可靠性验证

图8为信道类型为AWGN信道时合法接收方和非法接收方对接收信号进行解调的误码率性能曲线。可以看到合法接收方误码性能曲线几乎重合于QPSK理论误码性能曲线。说明混沌安全传输并不影响OFDM系统的接收性能。

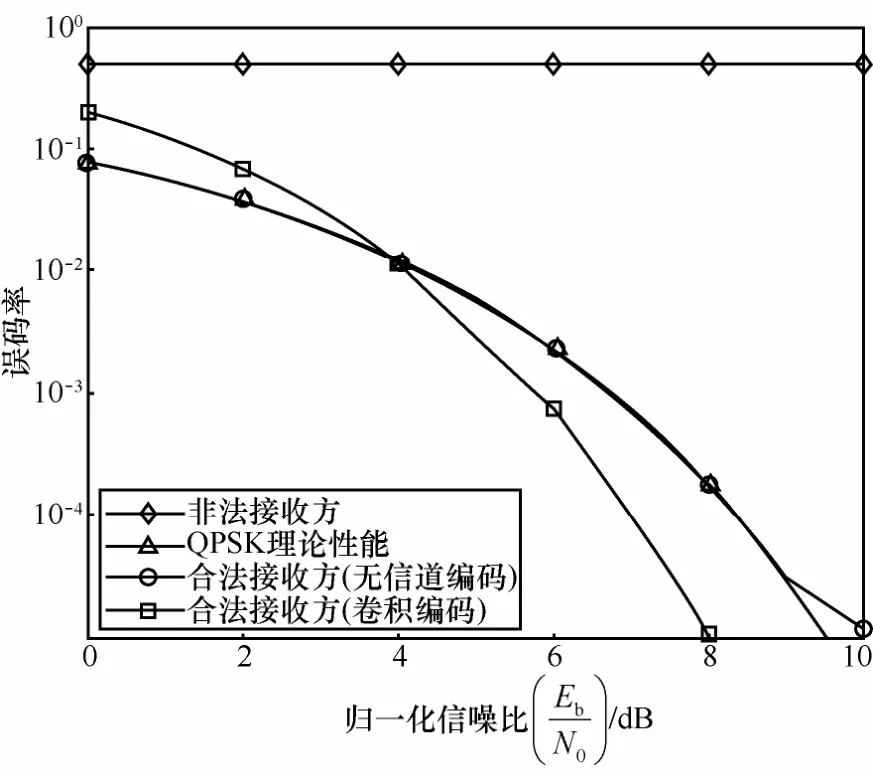
图8 AWGN信道的误码率性能

图9为信道类型是瑞利快衰落信道时合法接收方和非法接收方对接收信号进行解调的误码率性能曲线。可以看出，使用ZF均衡，其误码性能比单重接收分集理论性能略差，使用MMSE均衡时，误码性能接近于十重接收分集的理论性能。

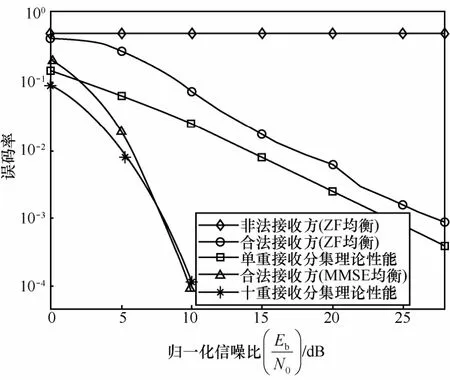
图9 瑞利快衰落信道的误码率性能

图10给出了信道类型为3GPP SCME信道模型（城区环境）时合法接收方和非法接收方对接收信号进行解调的误码率性能曲线，以及不同车速下合法接收方解调的误码性能对比情况。

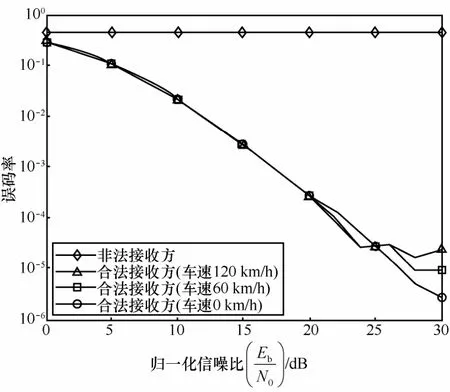
图10 频率选择性衰落信道的误码率性能

在理想信道估计场景下的3种信道模型，非法接收方在不知具体加密措施的情况下无法得到真实信息，增强了空口传输数据的可靠性和安全性。

5 结束语

本文针对OFDM通信系统的无线空口安全传输问题，提出了基于混沌映射的相位混沌旋转和子载波混沌选择的安全传输方案。该方案具有如下优点。

1) 利用混沌映射原理，增强OFDM无线传输系统的通信安全性，在有效对抗多径衰落、码间干扰，保证通信可靠性的同时，兼顾空口传输信息的安全性。

2) 混沌映射的方法有多种，采用2种混沌映射方法混合的方式增加了映射后信号的随机性，以及对初值和系数的敏感性，只有在混合密钥都获知的情况下，才有可能破解出原始信息。

3) K1、K2属于轻量级密钥（取决于混沌映射的初始值，分形参数及预迭代次数），方便密钥传递。

4) 相比于传统的OFDM系统，仅仅增加了与发送数据量呈线性的计算复杂度，不占用额外的带宽资源和时隙资源，不会破坏OFDM系统频带利用率的高效性和频带资源分配的灵活性。

[1] SHANNON C E. Communication theory of secrecy systems[J]. Bell System Technical Journal, 1949, 28(4)： 656-715.

[2] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3)：3-55.

[3] DACHSELT F, SCHWARZ W. Chaos and cryptography[J]. IEEE Trans. on Circuits and Systems I： Fundamental Theory and Applications, 2001, 48(12)： 1498-1509.

[4] SARKAR M, CHAUDHURI R R, CHOWDHURY S D, et al. Onset of chaos for different non linear systems by varying system parameters[M]. Advances in Optical Science and Engineering. Springer India,2015： 383-396.

[5] ZHANG H, WANG X F, LI Z H, et al. A new image encryption algorithm based on chaos system[C]//IEEE Inter Conf on Robotics, Intelligent Systems and Signal Processing. c2003：778-782.

[6] ALVAREZ G, MONTOYA F, ROMERA M, et al. Breaking two secure communication systems based on chaotic masking[J]. IEEE Trans on Circuits and Systems-II,2004, 51(10)： 505 -506.

[7] OZDEMIR M K, ARSLAN H. Channel estimation for wireless OFDM systems[J]. IEEE Commu Surveys & Tutorials, 2007, 9(2)： 18-48.

[8] KHAN M A, ASIM M, JEOTI V, et al. Chaos based constellation scrambling in OFDM systems： security & interleaving issues[C]//IEEE Inter Sympos on Information Technology. c2008：1-7.

[9] LIU B, ZHANG L, XIN X. Physical layer security in OFDM-PON based on dimension transformed chaotic permutation[J]. IEEE Photonics Technology Letters, 2014, 26(2)： 127-130.

[10] ZHANG L J. Theory and performance analyses in secure CO-OFDM transmission system based on two-dimensional permutation[J]. IEEE Photonics Technology Letters, 2013, 31(1)： 74 -80.

[11] LUENGO D, SANTAMARIA I. Secure communications using OFDM with chaotic modulation in the subcarriers[C]//IEEE Vehicular Technology Conference. c2005： 1022-1026.

[12] 廖旎焕, 高金峰. 广义映射混沌扩频序列及其特性分析[J]. 电子与信息学报. 2006, 28(7)： 1255-1257.LIAO N H, GAO J F. The chaotic spreading sequences generated by the extended chaotic map and its performance analysis[J]. Journal of Electronics & Information Technology, 2006, 28(7)： 1255-1257.

[13] 范九伦, 张雪锋. 分段 Logistic混沌映射及其性能分析[J]. 电子学报, 2009, 37(4)： 720-725.FAN J L, ZHANG X F. Piecewise logistic chaotic map and its performance analysis[J]. Acta Electronica Sinica, 2009, 37(4)： 720-725.

[14] SHIU Y S, CHANG S Y, WU H C, et al. Physical layer security in wireless networks： a tutorial[J]. IEEE Wireless Communications, 2011,18(2)： 66-74.

Secure OFDM transmission scheme based on two-stage chaos mapping

WANG Ying1, ZHANG Xiao-zhong1,2, ZENG Juan1,2, WANG Yong-ming1
(1. Institute of Information Engineering，Chinese Academy of Sciences, Beijing 100093, China;2.University of Chinese Academy of Sciences, Beijing 100049, China)

A secure OFDM transmission scheme based on two-stage chaos mapping was introduced, which were chaoticphase rotation and sub-carrier chaos mapping. The characteristics of pseudo-random and sensitivity to initial conditions of chaos sequences were employed. Numerical results and analysis show that the scheme canensure secure information transmission,and improve the pseudo-randomness of transmitted signals. The eavesdropper cannot estimate the message from statistic characteristics of

signals, which guarantees the communication security. Compared with traditional methods like advanced encryption standard, randomization of MIMO transmission coefficients, the scheme shows favorable computation security.

secure communication, chaos mapping, OFDM, phase rotation modulation, sub-carrier mapping

The National Natural Science Foundation of China (No.61501459)

TN918.91

A

10.11959/j.issn.1000-436x.2016141

2015-10-16；

2016-04-11

国家自然科学基金资助项目（No.61501459）

王颖（1987-），女，河南信阳人，博士，中国科学院助理研究员，主要研究方向为5G新型编码调制、无线物理层安全。

张晓忠（1992-），男，河北南皮人，中国科学院硕士生，主要研究方向为通信系统与安全。

曾娟（1991-），女，湖北广水人，中国科学院硕士生，主要研究方向为通信系统与安全。

汪永明（1968-），男，湖北广水人，博士，中国科学院正高级工程师、博士生导师，主要研究方向为通信系统与安全。