部分精英策略并行遗传优化的神经网络盲均衡

王尔馥，郑远硕，陈新武

（黑龙江大学电子工程学院，黑龙江 哈尔滨 150080）

部分精英策略并行遗传优化的神经网络盲均衡

王尔馥，郑远硕，陈新武

（黑龙江大学电子工程学院，黑龙江 哈尔滨 150080）

针对高维非凸代价函数下神经网络盲均衡算法收敛速度慢、容易陷入局部极小值的缺点，提出了一种组群并行遗传优化神经网络的方法。根据神经网络拓扑结构进行个体编码，设置控制码和权重系数码以实现对网络拓扑结构和网络权重同时优化。优化迭代过程中根据适应度对个体排序分组，以融合不同遗传算子条件下遗传算法的优势。部分精英策略有效避免最优个体把持进化过程引发早熟的现象。非线性信道条件下的仿真结果证明方法具有更好的收敛性能。

盲均衡；遗传算法；神经网络；精英策略

1 引言

盲均衡技术具有不需要训练序列即可实现对信道补偿和跟踪的特性，提高通信质量的同时能够有效节省通信带宽，提高通信效率[1]，因此，盲均衡技术在协作通信和非协作通信领域中均具有潜在的应用价值。利用常数模算法代价函数的神经网络盲均衡在解决非线性信道盲均衡问题中表现出稳健收敛性能。但是神经网络盲均衡常采用误差反传算法，在高维非凸代价函数条件下收敛速度慢，收敛后具有较大的稳态剩余误差，容易陷入局部极小值[2]。遗传算法根据生物进化准则提供了一种解决大规模复杂问题的优化方法[3]。盲均衡可以等效为代价函数最小化的极值问题，因此可以利用遗传算法进行优化处理。遗传算法在优化问题求解中面临几个难题目前仍无法有效解决，其中，包括计算复杂度过高、实时处理能力差、遗传算子初始化参数设置缺乏理论依据、需要人工经验等。本文在对遗传优化神经网络盲均衡算法分析的基础上，提出了一种组群并行遗传优化算法，由于遗传算法计算复杂度主要取决于种群规模，采用组群并行计算方法可有效降低计算复杂度[4]。在遗传算法参数初始化中，对每组子种群设置不同的遗传算子参数，进化过程中子种群间个体依据适应度值排序重组，充分融合不同遗传算子条件下遗传算法的优势，同时与直接精英策略遗传算法比较可有效避免早熟现象。遗传算法中个体根据神经网络拓扑结构进行编码，设置控制码和权重系数码，对神经网络盲均衡器的连接权重和拓扑结构同时优化。最后，利用计算机仿真证明了部分精英策略遗传优化的神经网络盲均衡与传统遗传算法和精英策略遗传算法优化的神经网络盲均衡相比，具有更好的收敛性能。

2 神经网络盲均衡基本原理

通信系统中，发射信号经过多径信道传输在接收端会产生码间干扰，严重影响通信质量[5]。均衡技术就是在接收机前设置一个滤波器，实现对多径信道的补偿和跟踪，实现消除码间干扰的目的。在很多通信场合中，通信信道具有非线性特性，此时利用线性结构均衡器难以获得理想的均衡结果。神经网络作为一种非线性动态系统，在非线性信道均衡中表现出稳健的收敛性能。图1给出了神经网络盲均衡的基本原理[6]。发射信号x( n)经未知信道h( n)并叠加高斯白噪声n( n)，在均衡器前得到观测序列y( n)。盲均衡的目标就是仅仅根据观测序列y( n)实现对发射信号x( n)的恢复，需要的先验信息为发射信号具有非高斯性。

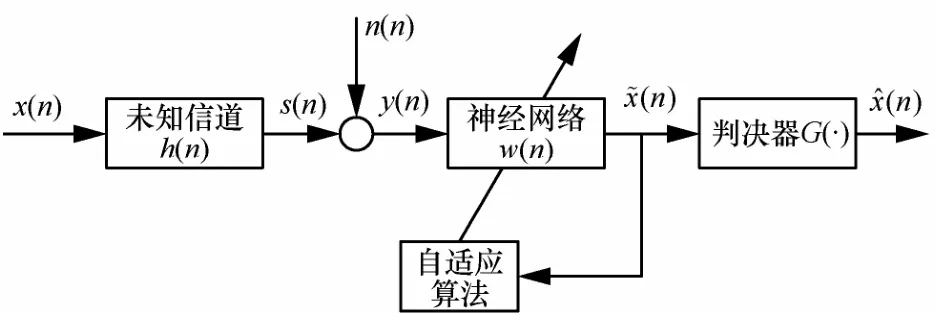
图1 神经网络盲均衡基本原理

神经网络盲均衡利用神经网络作为盲均衡器，根据输出信号x˜( n)的某种非线性变换构建代价函数，采用自适应算法更新网络权值，使代价函数最小化，实现对未知线性或非线性信道h( n)的补偿和跟踪。在神经网络盲均衡中，盲均衡器经常采用的是前馈神经网络[7]和小波神经网络[8]，小波神经网络在前馈神经网络的基础上嵌入了小波变换，在很多应用场合中表现出更快的收敛速度和收敛精度。2种神经网络在结构上没有太多不同，因此采用遗传算法进行优化时仅仅体现为编码个体上的差别。本文以前馈神经网络盲均衡优化进行推导说明，并将部分精英策略的遗传算法优化推广至小波神经网络盲均衡算法中，三层前馈（小波）神经网络盲均衡的结构如图 2所示[9]，其中， wij( n)为输入层至隐层的连接权重（为隐层至输出层的连接权重。

设隐层的输入为 uj( n)，输出为 Ij(n)，输出层的输入为v( n)，输出为˜x( n)，则根据网络的传输公式可以获得网络的状态方程为[10]

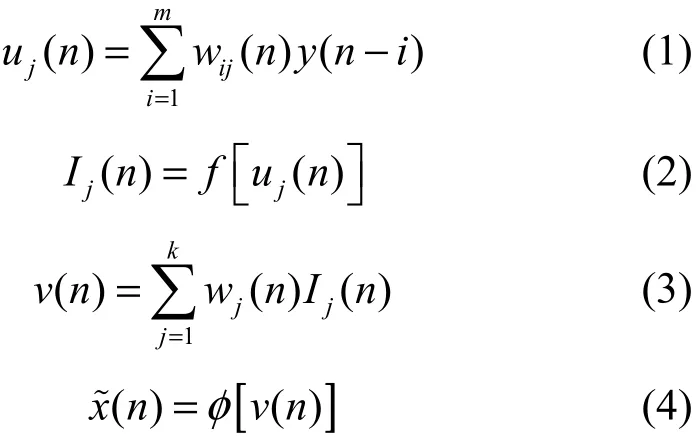
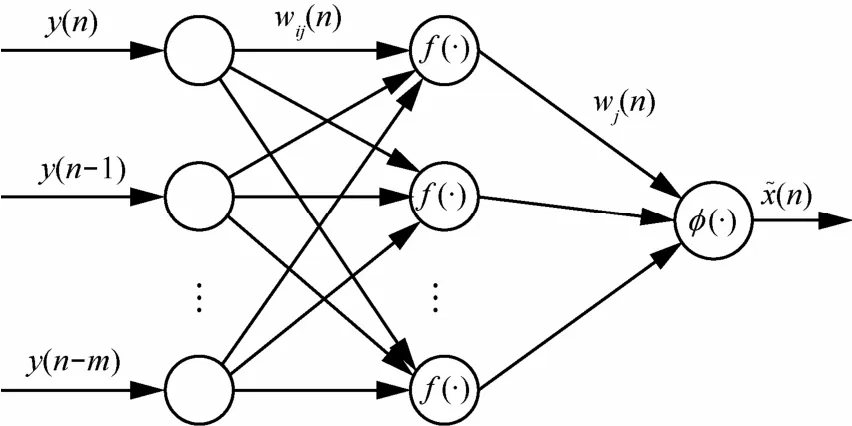
图2 三层前馈（小波）神经网络盲均衡器结构

其中， f(⋅)表示神经网络隐层单元的输入和输出之间的传递函数，φ(⋅)表示输出层的输入和输出之间的传递函数。如果隐含层传递函数f(⋅)为小波函数，则前馈神经网络为典型的紧致型小波神经网络。在神经网络盲均衡中，比较合理的传递函数设计方案是隐含层选择非线性变换函数或小波函数，输出层选择线性传递函数。本文选择前馈神经网络隐含层传递函数为

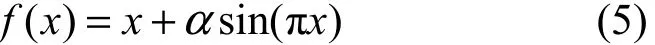
其中，0<α<1。小波神经网络隐含层传递函数为Morlet小波函数

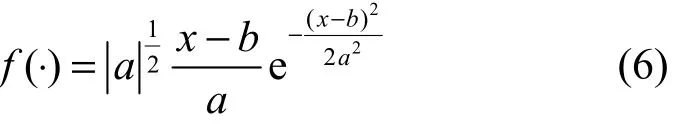
其中，a和b分别为小波变换的尺度因子和平移因子。无论是前馈神经网络还是小波神经网络，典型

的学习算法是采用基于梯度下降的误差反传（BP）算法。结合常数模 CMA2-2可设定神经网络的代价函数为[11]

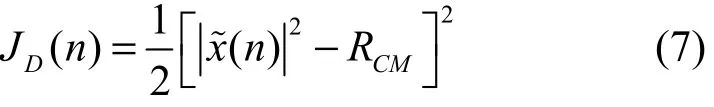
其中，RCM为常模，根据式（8）进行计算。

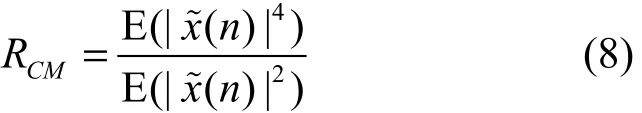
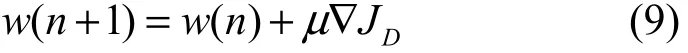
其中，∇JD为当前网络权重的瞬时梯度，µ为学习步长。对于小波神经网络的平移因子和尺度因子的更新，可采用同样方法。

根据BP算法，神经网络权值更新公式为

3 部分精英策略遗传算法实现

已经证明常数模CMA2-2代价函数是高维非凸的[12]，具有多个极值点。BP算法本质上属于随机梯度下降算法[13]，在高维非凸代价函数条件下的收敛性能依赖于初始搜索点和学习步长。目前为止，神经网络合理初值的设置没有理论依据指导，这直接导致基于BP算法的神经网络收敛速度慢，容易陷于局部极小值，在盲均衡中难以获得理想的均衡性能。遗传算法根据生物进化理论，通过种群中群体间选择、交叉和变异等操作，可实现对高维非凸代价函数极值化问题的优化求解。遗传算法的初始化参数设置直接影响遗传算法优化的性能，常规遗传算法在进化中对群体中所有个体采用相同的初始化参数，直接导致大量个体集中在同一个极值点上，在求解多峰值优化问题时，仍然具有陷入局部极小值的风险。并行遗传算法的设计最初是从减小遗传算法的计算复杂度上考虑的，但是每个子种群之间仍然采用相同的进化算子，即每个子种群中具有同样的进化环境，虽然减小了计算复杂度，但是全局寻优能力提高有限。小波神经遗传算法考虑到了种群中个体间进化的相似度，利用共享函数对个体适应度进行修正，避免了大量个体过于集中，从而保持进化过程中样本的多样性[14]，但是仍然没有考虑初始化算子参数对遗传算法性能的影响。基于并行遗传算法的设计思想，本文提出了一种部分精英策略的遗传优化算法，将种群划分为一系列子种群，各子种群利用不同的遗传算子参数。进化过程中对子种群间个体按适应度大小排序重组，进行部分交叉，称为部分精英策略。部分精英策略的并行遗传优化神经网络盲均衡的实现流程如图3所示。首先根据神经网络盲均衡问题构建遗传算法的适应度函数，遗传算法适应度函数朝着大的方向进化，因此可根据 CMA2-2代价函数设定遗传算法代价函数为

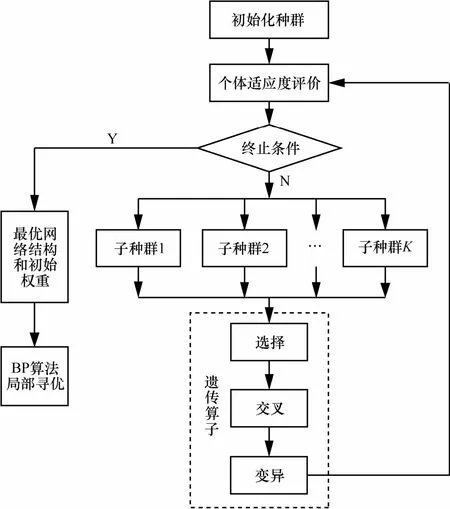
图3 部分精英策略并行遗传优化神经网络盲均衡流程

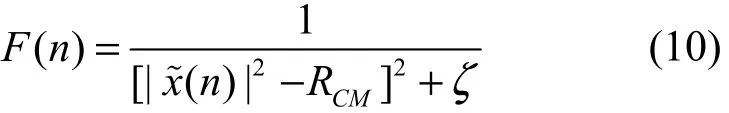
其中，ζ为一小的正常数，以防止出现式(10)被零除的现象。为实现对神经网络拓扑结构和网络权重的同时优化，将个体编码分为控制码和权重系数码，设三层神经网络拓扑结构为m×k×1，对于前馈神经网络，个体编码格式为如果为小波神经网络，个体编码格式为其中，ci为控制码， wi为权重系数码，在小波神经网络中，a和b分别表示小波函数的尺度因子和平移因子。对于控制码和权重系数码均采用实数编码方法，控制码的阈值为[0,1]，当 ci> 0.5，视为对应的网络权重有连接，否则将对应的网络连接权重置零，表示无连接。计算个体适应度函数，根据适应度函数从大到小对个体进行排序，将个体分为K组，从而建立K组子种群。分组规则为按适应度从大到小划分等差序列的方法，即每组个体按适应度大小划分为其中，S表示个体，下标i+K表示该个体按适应度大小的排序，i表示第i组子种群，N为种群规模。为了简化程序设计，人为设定种群规模与子种群数目的关系N为正整数。在子种K群中，根据精英策略，最优个体不参加交叉和变异，在本文中，一次进化过程中将有K个最优个体不参加交叉和变异操作，称为部分精英策略进化算法。通过个体按优劣进行了分组处理，并送入不同遗传算子参数的子种群中进行并行进化的策略，使个体在不同的进化环境中交叉进化，部分精英策略融合了不同遗传算子参数的优化性能，从而实现了一种并行部分精英策略的遗传优化方法。在子种群中，遗传算法的选择、交叉和变异操作根据文献[15]进行，算法的选择概率pK依据排序选择法设定。算法的变异概率pm对算法的收敛性能具有重要影响，根据分组规则，对于整体适应度较大的子种群选择较小的变异概率，而对于整体适应度较小的子种群选择较大的变异概率，按照整体适应度从大到小等差序列设定子种群的变异概率，即

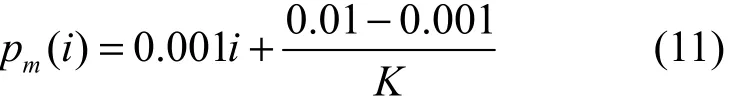
采用这种变异算子规则的理由是，对于整体适应度较大的子种群保持较小的变异概率，以保持进化的稳定性，而对于整体适应度值较小的子种群保持较大的变异概率，加快进化进程，以提高收敛速度。

对于同一优化问题，在适应度函数与编码规则确定的情况下，遗传算法的计算复杂度取决于种群规模N，在常规遗传算法中，计算复杂度为O( N3)。因此，对于本文提出的部分精英策略遗传算法的计算复杂度为显然这种并行部分精英策略的遗传优化方法可以有效降低算法的计算复杂度。尽管并行部分精英策略遗传优化算法计算复杂度较常规遗传算法有所降低，但是对于通信均衡系统而言，计算量仍然过大，且遗传算法不适用于解的微调。因此利用最大迭代步数和适应度函数目标值来控制遗传算法终止，进而利用梯度下降算法对神经网络盲均衡器进行更新，实现最终算法的精细求解。

4 数据仿真及分析

为了验证文中提出的并行部分精英策略遗传优化的前馈（小波）神经网络盲均衡（PEGA-FNN）（PEGA-WNN）的有效性，在相同仿真条件将其与基于 BP算法的前馈（小波）神经网络盲均衡（SGD-FNN，SGD-WNN）、常规遗传算法（GA-FNN，GA-WNN）和精英策略遗传算法优化（EGA-FNN，EGA-WNN）的神经网络盲均衡分别进行了比较。仿真中发送信号以等概率二进制随机序列生成，采用QPSK调制方式。神经网络拓扑结构设定为15× 12× 1，遗传算法中种群规模设置为N= 100，适应度函数中的常数因子 ζ= 0.000 1。在并行部分精英策略遗传算法中，子种群数目k= 5。常规遗传算法和精英策略遗传算法中选择概率 pc= 0.8，变异概率 pm= 0.006。直接BP算法中学习步长均设定为 µ= 0.001，在遗传优化后的梯度下降算法中设定学习步长 µo=0.000 1。非线性信道的输出为

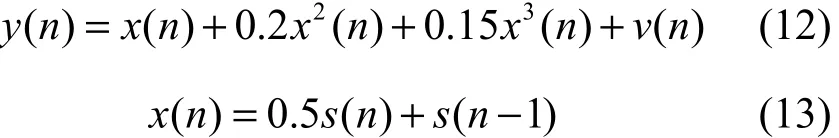
其中，y( n)为信道的输出，s( n)为信道的输入，v( n)为带限高斯白噪声。信噪比 SNR= 24 dB 的仿真条件下，进行500次蒙特卡洛仿真，以均方误差（MSE）对算法性能进行评价。

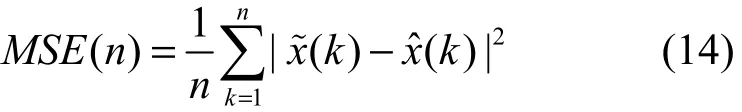
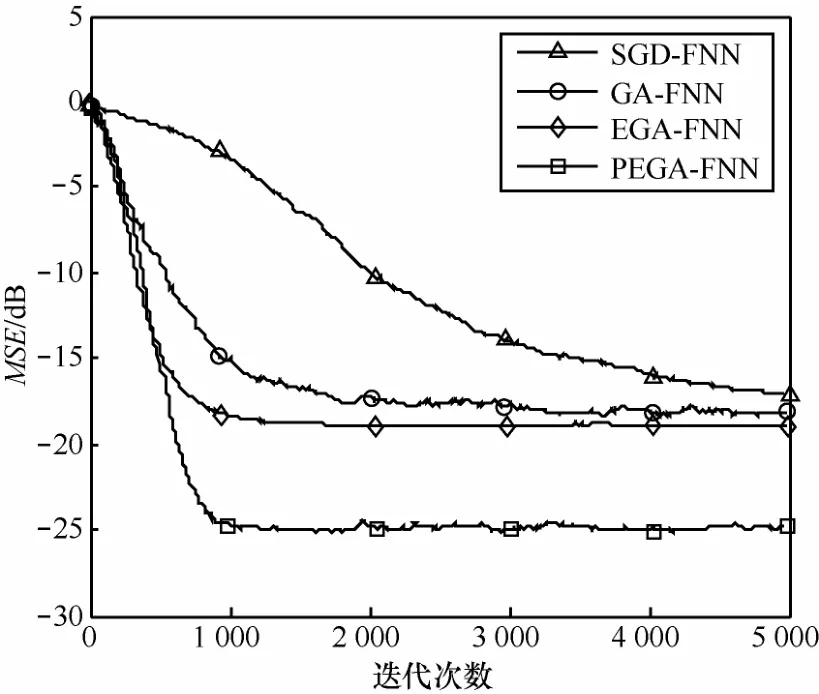
图4 遗传优化的前馈神经网络盲均衡性能比较

图4和图5分别比较了不同遗传优化方法的前馈神经网络和小波网络盲均衡的均方误差收敛曲线，可以看出，由于小波网络中嵌入了小波变换过程，因此在整体性能上，小波网络的均衡性能优于前馈神经网络。而本文提出的部分精英策略遗传优化的神经网络盲均衡在前馈神经网络和小波网络中均具有小的收敛后稳态剩余误差，在前馈神经网络和小波网络盲均衡算法中，部分精英策略遗传优化后的均方误差与直接精英策略遗传优化方法比较，均方误差分别降低了7 dB和5 dB。证明了本文提出算法的有效性。

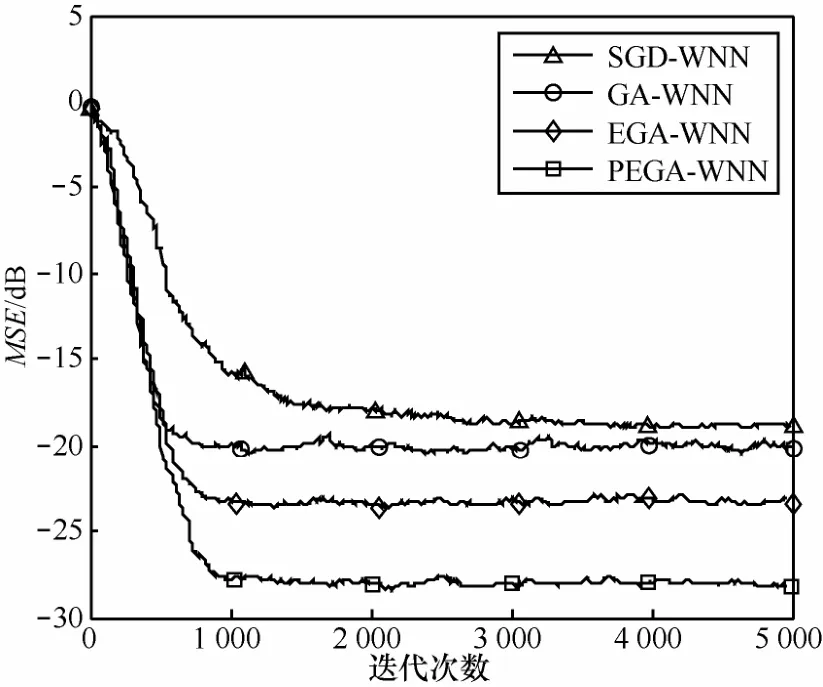
图5 遗传优化的小波网络盲均衡性能比较

为说明算法的计算复杂度，在相同计算机仿真条件下，统计算法执行所消耗的时间，统计结果如表1所示。从仿真结果中可以看出，采用并行策略的PEGA-FNN算法有效降低了GA-FNN的计算复杂度。

表1 算法运算时间比较结果

综上，部分精英策略并行遗传优化算法继承了精英进化策略快速收敛的优势，同时结合并行计算降低了计算复杂度，保持进化过程中样本的多样性，提高了全局优化能力。本文以该方法优化神经网络实现通信信道盲均衡只作为方法验证途径，所提方法可推广应用到系统辨识、模式识别等相关领域，特别是对于样本规模庞大、优化对象模型复杂的优化问题，从全局收敛性能和计算复杂度上有望获得更佳结果。

5 结束语

本文在神经网络盲均衡的模型基础上，提出了一种可同时优化神经网络拓扑结构和网络权重的部分精英策略遗传优化神经网络盲均衡算法。算法中将遗传算法种群按适应度函数进行排序重组，子种群各自采取精英策略进化，同时各种群设置不同变异概率以创造多样性的进化环境，在一定程度上克服了直接精英策略算法容易早熟问题，同时融合了不同变异算子下遗传算法的性能。算法在减小计算复杂度的同时，有效提高了全局收敛性能。利用前馈神经网络和小波神经网络盲均衡仿真验证了方法的有效性。

[1] PINCEMIN E, BROCHIER N, SELMI M, et al. Novel blind equalizer for coherent DP-BPSK transmission systems： theory and experiment[J]. IEEE Photonics Technology Letters, 2013, 25(18)：1835-1838.

[2] 郭业才, 樊康, 徐文才, 等. 基于混合遗传优化的正交小波变换盲均衡算法[J]. 数据采集与处理, 2011, 26(5)： 503-507.GUO Y C, FAN K, XU W C, et al. Hybrid blind equalization algorithm based on genetic algorithm and wavelet transform[J]. Journal of Data Acquisition & Processing, 2011, 26(5)： 503-507.

[3] 廖娟, 郭业才, 刘振兴, 等. 基于遗传优化的正交小波分数间隔盲均衡算法[J]. 兵工学报, 2011, 32(3)： 268-273.LIAO J, GUO Y C, LIU Z X, et al. A fractionally spaced blind equalization algorithm based on orthogonal wavelet transform and genetic optimization[J]. Acta Armamentarii, 2011, 32(3)： 268-273.

[4] 戴晓明, 邹润民, 冯瑞, 等. 混合并行遗传算法求解 TSP问题[J].电子与信息学报, 2002, 24(10)： 1424-1427.DAI X M, ZOU R M, FENG R, et al. A hybrid parallel genetic algorithm and its application to TSP[J]. Journal of Electronics and Information Technology, 2002, 24(10)： 1424-1427.

[5] NAFTA A, JOHANNISSON P, SHTAIF M. Blind equalization in optical communications using independent component analysis[J].Journal of Lightwave Technology, 2013, 31(12)： 2043-2049.

[6] 姜春艳. 遗传优化神经网络算法在信道盲均衡中的应用[J]. 计算机仿真, 2011, 28(11)： 145-147.JIANG C Y. Application of genetic neural network in blind equalization[J]. Computer Simulation, 2011, 28(11)： 145-147.

[7] 郭业才, 高敏, 张艳萍. 基于正交小波包变换的前馈神经网络盲均衡算法[J]. 电子测量与仪器学报, 2011, 23(11)： 59-64.GUO Y C, GAO M, ZHANG Y P. Feedforward neural network blind equalization algorithm based on orthogonal wavelet packet transform[J]. Journal of Electronic Measurement and Instrument, 2011,23(11)： 59-64.

[8] 郭业才, 王丽华. 模糊神经网络控制的混合小波神经网络盲均衡算法[J]. 电子学报, 2011, 39(4)： 975-980.GUO Y C, WANG L H. A hybrid wavelet neural network blind equalization algorithm based on fuzzy controlling[J]. Acta Electronica Sinica, 2011, 39(4)： 975-980.

[9] SUN Y S, ZHANG L Y, ZHANG J, et al. Neural network blind equalization algorithm applied in medical CT image restoration[J].Mathematical Problems in Engineering, 2013, (2013)： 1-10.

[10] XIAO Y, LI Z X. Wavelet neural network blind equalization with cascade filter based on RLS in underwater acoustic communication[J].Information Technology Journal, 2011, 10(2)： 2440-2445.

[11] ABRAR S, ALI A, ZERGUINER A, et al. Tracking performance of two constant modulus equalizers[J]. IEEE Communications Letters,2013, 17(5)： 830-833.

[12] ASHARIF F, TAMAKI S, ALSHARIF M R, et al. Performance improvement of constant modulus algorithm blind equalizer for 16 QAM modulation[J]. ICIC Express Letters, 2013, 7(4)： 1377-1383.

[13] 宋翀绂, 王宝树. 提高前馈神经网络学习效率的学习算法探讨[J].西安电子科技大学学报, 1999, 26(5)： 545-548.SONG C F, WANG B S. Improvement on the efficiency of the learning algorithm for multilayer feedforward neural networks[J]. Journal of Xidian University, 1999, 26(5)： 545-548.

[14] ZAOUCHE A, DAYOUB I, ROUVAEN J M. Baud-spaced constant modulus blind equalization via hybrid genetic algorithm and generalized pattern search optimization[J]. International Journal of Electronics and Communications, 2008, 62： 122-131.

[15] 肖瑛, 刘国枝, 李振兴, 等. 遗传优化神经网络的水声信道盲均衡[J]. 应用声学, 2006, 25(6)： 340-345.XIAO Y, LIU G Z, LI Z X, et al. Blind equalization for underwater acoustic communication by genetic algorithm optimizing neural network[J]. Applied Acoustics, 2006, 25(6)： 340-345.

Neural network blind equalization optimized by parallel genetic algorithm with partial elitist strategy

WANG Er-fu, ZHENG Yuan-shuo, CHEN Xin-wu
(Electronic Engineering College, Heilongjiang University, Harbin 150080, China)

Owing to the disadvantage of slow convergence and easy to fall into local minimum of the neural network blind equalization algorithm under high dimensional and non-convex cost function, a parallel genetic algorithm (GA)with partial elitist strategy was proposed to optimize neural network training. According to the neural network topology,individual coding, the control code and the weights were set up to realize the network topology structure and the network weights simultaneously. The individual group was sorted according to the adaptation degree of the optimization iterative process, in order to integrate the advantages of genetic algorithm under the conditions of different genetic operators.Some elite strategies effectively avoid the phenomenon of premature phenomena caused by the optimal individual control in the process of evolution. The simulation results under the nonlinear channel condition show that the method has better convergence performance.

blind equalization, genetic algorithm, neural network, elitist strategy

The National Natural Science Foundation of China (No. 61571181, No.61302074)

TN911.5

A

10.11959/j.issn.1000-436x.2016148

2016-05-01；

2016-06-14

国家自然科学基金资助项目（No.61571181, No.61302074）

王尔馥（1980-），女，黑龙江哈尔滨人，博士，黑龙江大学副教授、硕士生导师，主要研究方向为盲信号分离及盲均衡。

郑远硕（1994-），女，海南乐东人，黑龙江大学硕士生，主要研究方向为通信信号盲提取及数字化技术。

陈新武（1992-），男，福建仙游人，黑龙江大学硕士生，主要研究方向为盲均衡及其硬件实现。