基于共享资源量的动态多资源公平分配策略
张潇璐,刘曦,李伟东,张学杰
(云南大学信息学院,云南 昆明 650091)
基于共享资源量的动态多资源公平分配策略
张潇璐,刘曦,李伟东,张学杰
(云南大学信息学院,云南 昆明 650091)
针对云计算共享系统中多资源分配问题,提出一种基于共享资源量的动态多资源公平分配策略。该策略根据不同用户资源需求和共享资源量建立一个线性规划模型,同时证明该模型满足公平分配的4个重要属性:动态帕累托最优、激励共享、动态无嫉妒性和防止策略性操作,而且给出一种改进的动态多资源公平分配算法来提高算法运行效率。实验结果表明,所提动态多资源公平分配策略能够在满足任务资源需求的同时,尽可能保证公平分配下最大化占优资源份额,并且改进的分配算法能够有效地提高资源的分配效率。
云计算;多资源公平分配;占优资源;共享资源量
1 引言
云计算共享系统通过虚拟化技术将多种计算资源进行整合,实现资源的共享功能,为资源的统一管理和调度提供技术保证和条件。对云共享系统而言,资源分配调度是一个至关重要的组件。云共享系统根据当前各个虚拟机节点的资源需求,对资源进行合理分配,使虚拟机节点能够有足够的资源完成计算任务并保证用户之间公平有效地共享资源。因此,如何有效地将有限资源分配给各虚拟机节点,使云共享系统满足任务资源需求的同时兼顾资源分配的公平和效率是需要解决的关键问题。
目前,很多工作对资源公平分配问题进行了深入而广泛的研究。最常用的分配策略是最大最小公平模型(max-min fairness)[1],最早用于控制网络流量,以实现公平分配网络带宽。最大最小公平模型的基本思想是使资源分配的最小分配量尽可能最大化,防止任何网络流被“饿死”,同时在一定程度上尽可能增加每个流的速率。最大最小公平模型被认为是一种很好权衡公平性和有效性的自由分配策略,由此衍生出的大量算法被应用于各种资源分配上,包括网络带宽、CPU、内存等,但这些公平分配的研究主要集中在单一资源类型。
在云共享系统中,每个虚拟机节点的资源都是多维的,加上用户任务资源需求的多样性,相对于单一资源的分配,多资源类型的分配更难做到完全的公平性。另外,用户为了得到更多资源,可能通过需求欺骗、恶意占用等手段破坏资源分配的公平性,因此,多资源的公平合理分配显得尤为重要。已有的多资源公平分配研究成果中,DRF(DRF,dominant resource fairness)机制[2]被广泛应用到Hadoop Yarn[3]和Mesos[4]系统中。DRF计算每个用户每种资源的分配数量与资源总量的比值,所有比值中的最大值为该用户的占优资源份额(dominant share),与其相对应的资源为该用户的占优资源(dominant resource)。DRF机制的基本思想是最大化所有用户占优资源份额中的最小者,从而将多资源分配问题转化为单资源分配问题。该机制扩展了最大最小公平模型,使其能够在多种不同资源并存情况下保证分配的公平性。然而,DRF机制的提出是基于每个用户对资源池共享相同资源量的假设,在实际情况中,每个用户对资源的共享量可能不同,且共享量多的用户希望得到更多的资源。因此,文献[2]又提出加权DRF机制(weighted DRF),该机制对每个用户都关联一个共享资源量(权值向量),最大化用户得到的占优资源份额与其共享资源量的比值中最小值来实现资源的公平分配。如果所有用户的共享资源量相同,则加权DRF机制转换为DRF机制。
加权 DRF机制解决基于不同共享资源量的公平分配问题,但在实际云共享系统中,用户会在不同的时刻进入系统,用户带来的共享资源量使系统中可分配的资源总量发生动态变化,资源分配机制应该根据用户资源需求对资源分配情况进行重新调整,确保尽可能公平分配,而静态分配机制无法解决由用户动态性带来的资源分配公平性和效率问题。文献[5]针对资源分配的动态性做出较大改进,允许用户随时进入系统但不离开的情形,然而研究者也是基于用户进入云共享系统时带来相同资源份额的假设,并未考虑实际用户对资源共享的差异性所带来的公平性问题,并且在资源分配过程中采用注水(water filling)算法[5],该算法的运行时间复杂度是关于输入长度的伪多项式函数,操作性和用户资源需求与资源公平分配适应性比较差,从而导致比较低的资源分配效率。
针对上述问题,本文对动态情形下,用户的资源需求以及用户动态进入系统时所共享资源量的差异性带来的公平性和资源利用率问题做进一步综合考虑,面向云共享系统,提出基于共享资源量的动态多资源公平分配策略(DMFA-SRQ, dynamic multi-resources fair allocation based on shared resource quantity)。该策略基于用户资源需求和共享资源量,重新定义动态情形下占优资源份额,给出一个线性规划模型,在满足用户资源需求同时,尽可能实现占优资源的最大公平性分配,并且证明该模型满足公平分配的4个重要属性:动态帕累托最优(DPO, dynamic Pareto optimality)、激励共享(SI,sharing incentive)、动态无嫉妒性(DEF, dynamic envy freeness)和防止策略性操作(SP, strategy proofness);提出改进的动态多资源公平分配算法使算法运行时间复杂度减小到Ο ( n2logn)(n为系统中用户数)。理论和实验表明,本文提出的方法解决了动态情形下基于不同共享资源量的多资源公平分配问题,且有效提高了算法的运行效率。
2 相关工作
近年来,研究者们提出了各种各样有关公平性的资源分配算法。在单一资源类型的公平分配研究中,文献[6~9]研究 CPU时间、链路带宽资源的公平分配策略,利用“max-min fairness”思想,最大化每个用户分配到的最小资源,保证多数用户的资源需求得到满足,实现公平性分配。文献[10,11]研究在2个用户利益之间寻求资源分配平衡机制,提出“proportional fairness”方法;Zukerman等[12]提出针对单一资源在公平和效率之间进行折中的效用评估算法;Lan等[13]基于公平分配理论属性,提出一种资源分配机制,并为公平性的度量提供了准则。
在多资源公平分配研究中,Ghodsi等[2]最早系统地研究云计算系统中多资源公平分配问题,基于用户相同共享资源量的假设,提出一种DRF机制。该机制显示出诸多令人满意的公平属性,吸引了大量研究者的关注,并得到了广泛推广。Dolev等[14]提出基于瓶颈资源的公平分配(BBF, bottleneck based fairness)算法,并证明BBF满足激励共享和无嫉妒性2种公平属性;Gutman等[15]考虑DRF在多个效用模型下的通用性,并且能够在多项式时间内解决BBF公平分配问题;Bhattacharya[16]重新定义 DRF以此来支持多层次资源分配;Wang等[17]提出改进 DRF机制,使其能够适用于异构云计算环境;Joe-Wong等[18]推广 DRF,量化并使其成为一个一体化的框架,以权衡分配公平和分配效率;Psomans等[19]研究在多个计算节点上对离散任务的多资源公平分配方法;Parks等[20]用多种方法扩展DRF机制,适用于某些资源的零需求、不可划分任务和不同权重等情形。
以上工作都是基于系统中所有用户资源需求的静态分配,与目前云共享系统中用户随时进入和退出的动态性有本质的不同,而且资源分配过程中并没有考虑到历史分配信息。在动态情形下,Zeldes等[21]提出基于资源瓶颈和全局属性的在线公平分配机制;文献[22,23]分别在静态和动态情形下研究基于用户有限任务请求数量的多资源公平分配机制,但未解决在用户动态进入云共享系统时用户资源请求和共享资源量的差异性对多资源公平分配的影响。Kash等[5]虽提出基于用户相同共享资源量的多资源公平分配策略DDRF,但这种策略并没有考虑用户共享资源量的差异性所带来的实际资源分配的公平性和效率问题。
综上,虽然目前很多工作在多资源公平分配问题上取得了一定进展,但对用户动态性以及资源需求和共享资源量差异性带来的分配公平性和资源利用率问题缺乏进一步考虑,因此,本文引入一种基于共享资源量的动态多资源公平分配策略DMFA-SRQ,给出一个线性规划分配模型,并提出一种改进的动态多资源公平分配算法。
3 问题描述及相关定义
在云共享系统中,用户请求是由具有不同资源配置的虚拟机进行响应,为方便以下讨论,这里做个假定:用户任务的资源请求可认为是虚拟机资源请求,用户任务的资源分配过程即虚拟机资源部署过程。
假定云共享系统中资源池包含m种硬件资源,如CPU、内存、磁盘、网络带宽等。令 R = {1,2,…,m}表示资源种类集合, U= {1,2,…, n}表示用户集合。用户i的资源需求向量为 Di=(Di1,… , Dim),其中,Dij表示用户i的任务对资源j的需求量占整个资源池中资源j总量的比例,且 Dij> 0。对Di做归一化
令 wi表示用户i对资源池中每种资源的共享资源量,且当系统中有k个用户时,k ∈ {1,… ,n},令 xik表示用户i分配得到的占优资源份额数,即可执行的任务数。定义用户i的占优资源份额(dominant share)为
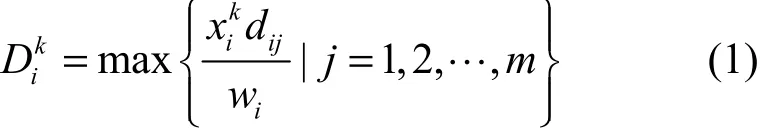
根据占优资源定义,上式可简化为
在动态情形下,假定用户在不同时刻顺序到达,即用户k在用户k−1之后到达,且用户(i>k)的资源需求di>k未知。用户进入系统后不会离开,并且每个用户任务所需资源量不会随时间发生改变。当系统中有k个用户时,得到一个动态多资源公平分配方案Ak=(Ak,… ,,… ,), 其 中 ,= (,…,
在资源j上分配得到的资源数量,满足以下公式

并且对任意用户i, i≤k− 1,k≥2,其分配结果是一个不可逆过程,即≥。对所有用户i, 给定一个分配 Ak,则在虚拟机上被调度执行的最大
ij任务数按如下公式计算
i + ij对任意资源 j, j∈R,若存在这样一个y,使=d y成立,则称 Ak为无浪费分配方案。ij ij
本文设计一种动态情形下无浪费资源分配方案:基于共享资源量的动态多资源公平分配策略(DMFA-SRQ),目标是当系统中存在k个用户时,最大化占优资源份额kM ,从而得到最大化的占优资源份额数,并且尽可能保证资源分配的公平性。因此,DMFA-SRQ策略可形式化为

该线性规划模型中第一个约束条件是尽可能保证占优资源的公平分配,同时,共享资源量越多的用户分配得到的占优资源份额数就越多。另外,还给出在多资源分配过程中其他2个约束条件,即当系统中有k个用户时,对任意用户分配得到的占优资源份额数不小于系统中有k−1个用户时的分配情况,满足分配的不可逆性;当系统中有k个用户时,系统可以分配的资源量最多为
图1举例说明DMFA-SRQ策略的资源分配情况。假设系统中共有3个用户,分别顺序进入系统。每个用户的资源需求向量和共享资源量分别为当系统中只有用户1时,分配得到的占优资源份额;当系统中
在静态分配情形下,根据文献[15,21]以及式(4)的线性规划方程组,可通过式(5)求得静态最优解
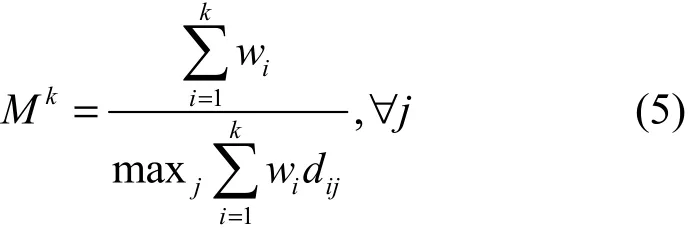
接下来提出一种快速算法 DMFA-SRQ以解决动态分配情形下kM 最大化问题。
4 DMFA-SRQ策略的公平性分析
无论是在云共享系统[2,19],还是在经济学[24,25]中,资源分配的效率和公平性被广泛认为是最重要的属性,也是衡量一个公平分配机制优劣的判断标准。文献[5]引入在动态情形下多资源公平分配机制所满足的4个重要属性:动态帕累托最优、激励共享、动态无嫉妒性、防止策略性操作。本文在此基础上,针对动态情形下用户资源需求以及用户共享资源量的差异所提出的公平分配机制应满足的4个重要属性做进一步讨论。
1) 动态帕累托最优
对于所有用户的可行分配方案 Ak,其中任意一个用户i的资源分配方案,有() >()成立, 那么将存在一个用户h,使 N () <()成立。
h
2) 激励共享
如果一种动态公平分配机制系统中有k个用户时,对任意用户i,i∈U ,i≤k,有 N (Ak)≥ N( w )
i i i i成立,则认为该机制满足SI属性。
3) 动态无嫉妒性
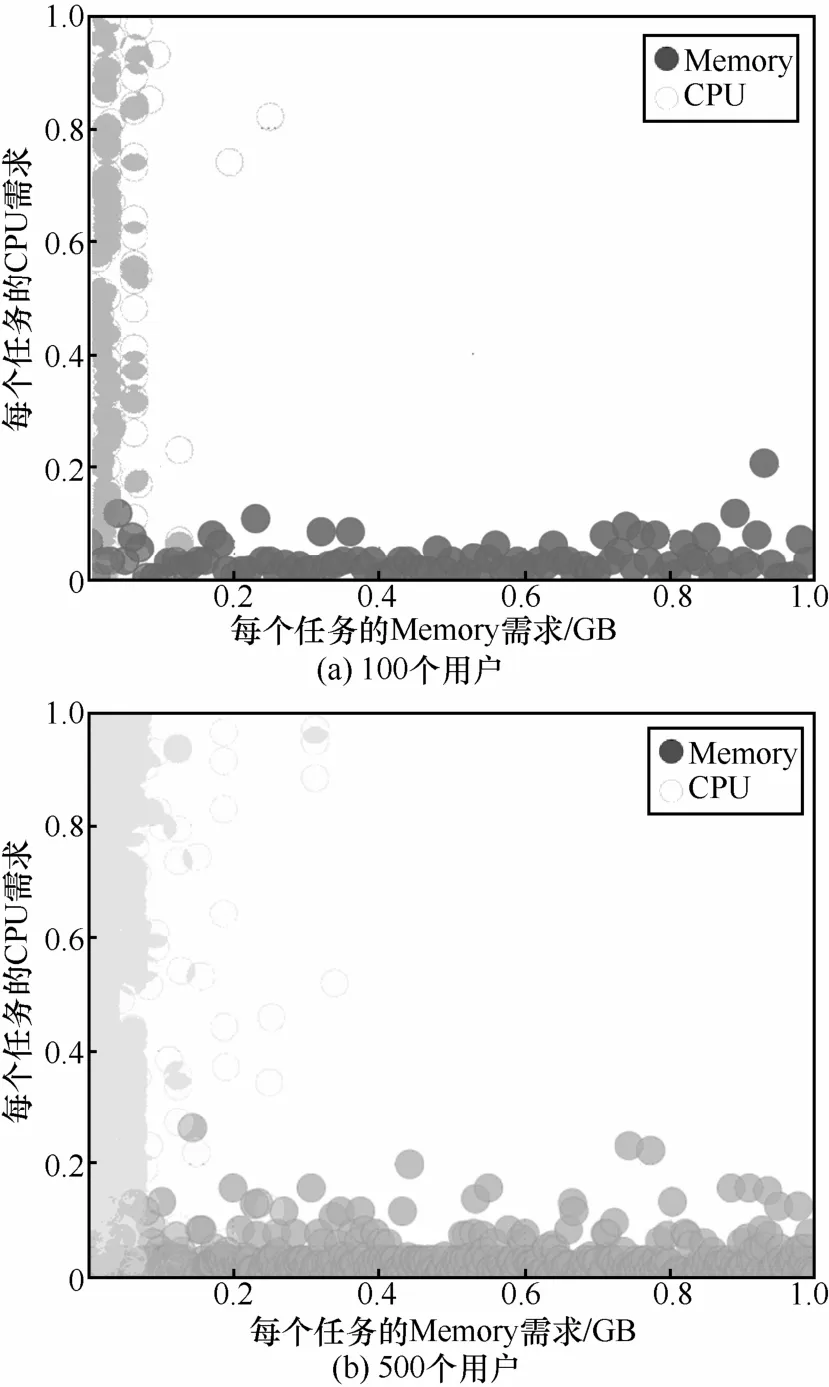
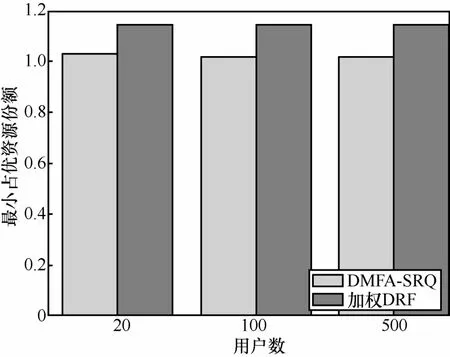
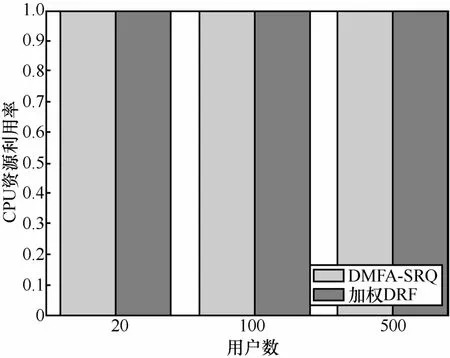
在动态公平分配机制中,如果用户i嫉妒用户h,i, h∈U,说明用户h是在用户i之前进入系统,并且自用户i进入系统之后用户h未再被分配资源,则该机制满足DEF属性。即当系统中有k个用户时,如果成立,则有h 4) 防止策略性操作 用户不能通过谎报资源需求来提高自己的占优资源份额,此属性满足需求不可欺骗性。令为用户i谎报虚假资源di,而其他用户都提交真实资源需求情况下得到的分配方案,则有i≤k成立。 图1 DMFA-SRQ策略的资源分配结果 DPO属性表明当用户资源分配已经达到饱和时,它可能在影响其他用户分配的前提下,增加自己的占优资源份额数。SI属性确保用户最终分配得到的占优资源份额数不少于用户带来的共享资源量,并且用户带来的共享资源量越多,分配到的资源就越多。DEF属性说明如果一种动态分配机制是有嫉妒性的,则用户会嫉妒比其早进入系统且分配到较多占优资源份额的用户。SP属性规定用户不能通过谎报自己的需求来获得更多额外资源。 引理1 当系统中有k个用户时,k ∈{1,…, n},对用户i,i∈U ,i≤k,=max{Mkw, xk−1}。 i i 证明 考虑系统中有k个用户时,根据式(4)中前 2个 约束 条 件≥Mkw, xk≥ xk−1,得 到i i i 证明 利用数学归纳法证明。当i>k,h>k时,== 0。假设当系统中有k−1个用户存在时, k ∈ {h, … , n},不等式成立。当系统中存在k个用户时,根据引理1及得出即证毕。 h则有根据h 从引理1可以看出,对系统中每个用户而言,不同资源需求的用户根据 DMFA-SRQ策略分配得到的占优资源份额随着更多用户在不同时刻进入系统后呈现单调非递减性。引理2表明用户得到的占优资源份额随着用户进入系统的先后顺序呈现单调非递增性。引理3则表示当系统中有k个用户时,如果用户h的占优资源份额大于用户i,说明用户h比用户i更早进入系统,且自用户i进入系统后,用户h未被再分配资源,因此,用户i会嫉妒用户h,这与动态无嫉妒属性(DEF)所描述的含义相同。下面根据以上的引理,验证 DMFA-SRQ策略满足4个重要属性:动态帕累托最优、激励共享、动态无嫉妒性、防止策略性操作。 定理1 当系统中有k个用户时,k ∈{1,…, n},DMFA-SRQ策略满足DPO属性。 证明 当系统中有k个用户时,至少存在一种资源 j(j∈R)和一个最优解 Mk,使式(4)中第3个约束条件成立。否则,如果存在一个不满足分配方案的用户i,在不影响其他用户分配情况下,提高自己分配到的占优资源份额数,即增加一个很小的量+ε,ε>0,使 Mk值也相应增加,与 Mk是问题最优解相矛盾,因此,DMFA-SRQ满足DPO属性。 定理2 当系统中有k个用户时,k ∈{1,…, n},DMFA-SRQ策略满足SI属性。 证明 考虑系统中只有一个用户时,根据式(4)中第1个约束条件,有=w1,M1=1,则可以得到≥ M1w ≥ w。接下来,利用数学归纳法证明 1 1当系统中有k个用户时, k ∈ {2,…, n},对任意用户i,i∈U ,i≤k,则有)≥wi),即≥wi。 定理3 当系统中有k个用户时,k ∈{1,…, n},DMFA-SRQ策略满足DEF属性。 证明 当系统中有k个用户时,如果对任意用户i, h≤k,用户i嫉妒用户h,即根据引理 3,则有由上述不等式可以推出否则,得出以下不等式 其中,j*为用户i的占优资源,由式(6)可知用户i得到比用户h更多的占优资源份额,与条件矛盾。因此,由及引理3可以推出DMFA- SRQ满足DEF属性。证毕。 接下来,证明DMFA-SRQ策略满足SP属性,首先,给出引理 4。当系统中有k个用户时,k ∈ {1,… , n},假设用户i,i∈U,谎报不真实的资源需求向量,则至少存在一个用户t,t∈ {i, … ,k},自加入系统之后使用户i获得比较多的优势份额数量。此时,对任意其他真实需求用户h,在不真实资源需求环境下分配得到的占优资源份额数表示为,h≤k,同时, Mˆk为求解线性规划方程式(4)得到的最优解。 证明 考虑以下2种情况。 定理4 当系统中有k个用户时,k ∈{1,… ,n},DMFA-SRQ策略满足SP属性。 证明 利用反证法证明。当系统中有k个用户时,用户i谎报不真实资源需求,当第t个用户进入系统时,用户i分配得到较多的优势份额数,则存在一种资源j,j∈R,使分配满足动态帕累托最优性质,并根据引理4可以推出以下不等式 不等式(7)与式(4)中第3个约束条件相矛盾,因此,DMFA-SRQ满足SP属性。证毕。 Water filling算法[5]是一种在动态情形下实现资源最大最小化公平分配的经典算法,但代价是算法运行时间过长。本文基于第3节中提出的线性规划模型,设计了一个更为快速的Ο ( n2logn)多项式时间复杂度算法,即用基于共享资源量的动态多资源公平分配算法改进求解最优分配方案的算法运行效率问题。 该算法基于本文定义的最大化 Mk以及约束条件,寻找一个用户τ对应的vτ,使如果> vτ成立, 则否则从而确定,并最终得到该算法主要思想如下。 1) 当系统中有k个用户时,对k−1个 xik−1值进行非递增排序(i 3) 根据式(4)线性规划方程组中前2个约束条件以及引理 1,当系统中有k个用户时,每个用户i被分配执行的任务数为,即从而最终得到用户i在资源 j上的分配方案。DMFA-SRQ算法的操作过程如算法1所示。 算法1 DMFA-SRQ算法 1) 输入:Demanddi,1≤i≤k 4)k←2; 7) 8) else, do 10) 12) 14) goto 10); 15) else, do 17) goto 10); 18) end if; 19) end while; 21) 24)k ←k+1; 25) end while 当系统中有k个用户时,本文提出的DMFA-SRQ 算法利用二分法思想确定vτ,并得到和最终分配方案(,… ,xk),算法的运行时间取k决于求解vτ值的迭代次数,因此,该算法的时间复杂度为Ο ( klogk)。当系统中共有n个用户时,整体算法运行时间为 实验将采用Google 集群中真实计算任务负载数据集[26]中500个任务类型文件中的143 601 184个任务运行所需的CPU和Memory资源作为本文实验中用户资源请求。实验从该数据集中随机选取20、100、500个用户,对每个用户的资源需求向量<CPU,Memory>进行归一化处理,并随机设置每个用户的共享资源量wi,使其满足其中,100、500个用户的资源需求分布如图 2所示。本文对所提DMFA-SRQ算法与加权DRF算法进行仿真模拟,实现2种算法的资源分配,并基于最小占优资源份额、占优资源份额数和、资源利用率3个最大化目标分别在不同用户数下各执行1 000次取均值得到2种算法的实验结果,以此来评估 DMFA- SRQ算法性能。 图2 用户资源需求分布 图3和图4分别给出了在100个、500个用户下,用户共享资源量对用户资源分配的影响。实验设置用户随机动态进入系统并随机设置其共享资源量 wi,满足 采样点均匀选取其中 20个用户分配得到的占优资源份额数,并对wi进行升序排列。从图3和图4中可以看出,用户共享资源量与占优资源份额数呈现单调非递减性,即用户共享资源量 wi越多,其分配得到的占优资源份额数就越多。该实验结果表明,DMFA-SRQ算法保证资源分配的公平性,并且共享资源量越多的用户,分配得到的资源也越多。 图3 100个用户下占优资源份额数基于wi的变化 图4 500个用户下占优资源份额数基于wi的变化 DMFA-SRQ算法目标是在尽可能保持公平分配情况下,最大化占优资源份额,因此,为进一步验证所提出的 DMFA-SRQ算法能够保证资源分配的公平性和分配效率,本文基于最小占优资源份额、占优资源份额数和、资源利用率3个最大化目标与静态情形下加权 DRF算法进行对比分析。 1) 最小占优资源份额最大化 i验分配结果如图5所示。 图5 最小占优资源份额 从图5中可以看出,动态情形下DMFA-SRQ算法得到的占优资源份额低于静态情形下加权DRF算法得到的结果,这主要是因为动态情形下用户资源需求未知,分配过程中无法比较所有用户的最小占优资源份额,而且动态分配需要满足分配的不可逆性条件。通过实验结果也可以看出,基于不同共享资源量的 DMFA-SRQ分配算法在不违背公平性原则的情况下,实现动态情形下最小占优资源份额最大化分配目标,也进一步验证了该算法满足SI属性。 2) 占优资源份额数和最大化 在经济学中,占优资源份额数和是衡量策略效率的一个重要指标[5]。当系统中有k个用户时,给出占优资源份额数和的定义为图 6 给出DMFA-SRQ算法与加权DRF算法的占优资源份额数和的对比。 图6 占优资源份额数和 从图6中可以看出,动态情形下的DMFA-SRQ算法分配得到的占优资源份额数和与静态加权DRF算法结果相接近,说明 DMFA-SRQ算法在满足式(4)线性规划方程组中的约束条件下,能够实现动态情形下所有用户占优资源份额最大化分配目标。 3) 资源利用率最大化 在云共享系统中,资源利用率是衡量分配策略效率的重要标准之一[14]。因此,本文测试DMFA-SRQ算法下的CPU和Memory资源利用率,并与加权DRF算法进行比较。图7和图8分别给出了2种算法的CPU和Memory资源利用率结果。 从图7和图8中2种算法资源利用率的对比可以看出,DMFA-SRQ算法下的资源利用率值与静态情形下的加权 DRF算法结果相接近,且用户数越多,2种算法的资源利用率越接近。实验结果验证本文所提算法的资源利用率并没有因为动态情形下用户资源需求未知以及资源共享总量的差异而有所降低,说明该策略既保证资源分配的公平性,又兼顾到分配效率。 图7 CPU资源利用率 图8 Memory资源利用率 本文针对云计算共享系统中虚拟化资源分配的公平性问题,基于用户资源需求和共享资源量,提出基于共享资源量的动态多资源公平分配策略。该策略建立一个线性规划模型来实现对占优资源的尽可能公平分配,并证明该模型满足公平分配的4个重要属性:动态帕累托最优、激励共享、动态无嫉妒性、防止策略性操作,此外,本文还提出基于共享资源量的动态多资源公平分配算法来改进算法运行效率。而且,本文所提出的策略和算法不仅可以应用于云共享系统资源的动态分配,也适用于WLAN和WSN等领域的网络带宽分配。最后,实验基于最小占优资源份额、占优资源份额数和、资源利用率最大化目标与加权 DRF算法进行比较,进一步表明本文所提DMFA-SRQ策略能够有效地保证动态情形下多用户多资源分配的公平性和资源利用率。但由于云计算环境的异构性以及资源分布在多服务器等复杂情况,还可能面临更为复杂的多资源分配问题,因此,对异构环境下的动态多用户多资源公平分配问题将是下一步的研究工作。 [1] Max-min fairness[EB/OL]. http://en.wikipedia.org/wiki/Max-min_fairness. [2] GHODSI A, ZAHARIA M, HINDMAN B, et al. Dominant resource fairness: fair allocation of multiple resource types[C]//The 8th USENIX Conference on Networked Systems Design and Implementation. c2011: 24. [3] Hadoop[EB/OL]. http://hadoop.apache.org/. [4] Mesos[EB/OL]. http://mesos.apache.org/. [5] KASH I, PROCACCIA A D, SHAH N. No agent left behind: dynamic fair division of multiple resources[J]. Journal of Artificial Intelligence Research, 2013(1): 351-358. [6] JAIN R, CHARNY A, CLARK D. Congestion control with explicit rate indication[C]// 1995 IEEE International Conference on Communications.c1995: 1954-1963. [7] GOYAL P, VIN H M, CHEN H. Start-time fair queueing: a scheduling algorithm for integrated services packet switching networks[C]//ACM Sigcomm Computer Communication Review. c1996: 157-168. [8] STOICA I, SHENKER S, ZHANG H. Core-stateless fair queueing:achieving approximately fair bandwidth allocations in high speed networks[C]//The ACM Sigcom. c1998: 118-130. [9] CAPRITA B, CHAN W C, NIEH J, et al. Group ratio round-robin: O(1)proportional share scheduling for uniprocessor and multiprocessor systems[C]//Usenix Technical Conference. c2005: 337-352. [10] KELLY F. Charging and rate control for elastic traffic[J]. European Transactions on Telecommunications, 1997, 8(1):33-37. [11] MASSOULIE L, ROBERTS J. Bandwidth sharing: objectives and algorithms[C]//18th Joint Conference of the IEEE Computer and Communications Societies(INFOCOM '99). New York. c1999: 1395-1403. [12] ZUKERMAN M, TAN L, WANG H, et al. Efficiency-fairness tradeoff in telecommunications networks [J]. IEEE Communications Letters,2005, 9(7):643 - 645. [13] LAN B T, KAO D, CHIANG M, et al. An axiomatic theory of fairness in network resource allocation[C]//IEEE Infocom. c2010: 1-9. [14] DOLEV D, FEITELSON D G, HALPERN J Y, et al. No justified complaints: on fair sharing of multiple resources[C]//The 3rd Innovations in Theoretical Computer Science Conference. c2012: 68-75. [15] GUTMAN A, NISAN A. Fair allocation without trade[C]//The 11th International Conference on Autonomous Agents and Multiagent Systems. c2012: 719-728. [16] BHATTACHARYA A A, CULLER D, FRIEDMAN E, et al. Hierarchical scheduling for diverse datacenter workloads[C]//The 4th Symposium on Cloud Computing (SOCC’13). c2013:1-15. [17] WANG W, LIANG B, LI B. Multi-resource fair allocation in heterogeneous cloud computing systems[J]. Parallel and Distributed Systems,2015, 26(10): 2822-2835. [18] JOE-WONG C, SEN S, LAN T, et al. Multiresource allocation: fairness-efficiency tradeoffs in a unifying framework[J]. IEEE/ACM Transactions on Networking, 2013, 21(6): 1785-1798. [19] PSOMAS C A, SCHWARTZ J. Beyond beyond dominant resource fairness: Indivisible resource allocation in clusters[R]. Technology Report, Berkeley, 2013. [20] PARKES D C, PROCACCIA A D, SHAH N. Beyond dominant resource fairness: extensions, limitations, and indivisibilities[J]. ACM Transactions on Economics and Computation, 2015, 3(1). [21] ZELDES Y, G.FEITELSON D. On-line fair allocations based on bottlenecks and global priorities[C]//The 4th ACM/SPEC International Conference on Performance Engineering. c2013: 229-240. [22] LI W D, LIU X, ZHANG X L, et al. Multi-resource fair allocation with bounded number of tasks in cloud computing systems[J]. Eprint Arxiv, 2014. [23] LI W, LIU X, ZHANG X, et al. Dynamic fair allocation of multiple resources with bounded number of tasks in cloud computing systems[J]. Multiagent and Grid Systems, 2016, 11(4): 245-257. [24] BARBANEL J B, BRAMS S J. Two-person cake-cutting: the optimal number of cuts[J]. Mathematical Inteuigencer, 2011, 36(3): 23-35. [25] LI J, XUE J. Egalitarian division under leontief preferences [J]. Economic Theory, 2013, 54(3): 597-622. [26] WILES J, REISS C. Google cluster data 2011_2[EB/OL]. https://code.google.com/p/googleclusterdata/. Dynamic fair allocation of multi-resources based on shared resource quantity ZHANG Xiao-lu, LIU Xi, LI Wei-dong, ZHANG Xue-jie A dynamic fair allocation of multi-resources was proposed based on shared resource quantity for multi-resoures allocation problem in cloud shared computing system. Firstly, a linear programming model was given based on resource requirements and quantity of shared resource and this model was further proved which satisfies four fairness properties such as DPO, SI, DEF and SP. Secondly, an improved dynamic multi-resources fair allocation algorithm was introduced for the allocation efficiency. Finally, theoretical analysis and experiments demonstrate that this strategy can satisfy the demands as well as maximize the dominant share on the base of approaching fairness and the improved algorithm increases the allocation efficiency in the dynamic system. cloud computing, multi-resources fairness allocation, dominant share, shared resource quantity s: The National Natural Science Foundation of China (No.61170222, No.11301466), Scientific Research Foundation of Yunnan Provincial Department of Education (No.2015J007), Natural Science Foundation of Yunnan Province (No.2013FB010) TP301 A 10.11959/j.issn.1000-436x.2016144 2015-11-19; 2016-04-20 国家自然科学基金资助项目(No.61170222, No.11301466);云南省教育厅科学研究基金资助项目(No.2015J007);云南省科技厅应用基础研究面上基金资助项目(No.2013FB010) 张潇璐(1983-),女,山东淄博人,云南大学博士生,主要研究方向为资源分配调度、云计算能耗、大数据处理。 刘曦(1987-),男,云南昆明人,云南大学博士生,主要研究方向为智能算法、资源分配调度、大数据处理。 李伟东(1981-),男,河南郑州人,博士,云南大学副教授,主要研究方向为组合优化算法、复杂性分析、分布式计算。 张学杰(1965-),男,云南昆明人,云南大学教授、博士生导师,主要研究方向为高性能计算、云计算、大数据、分布式计算。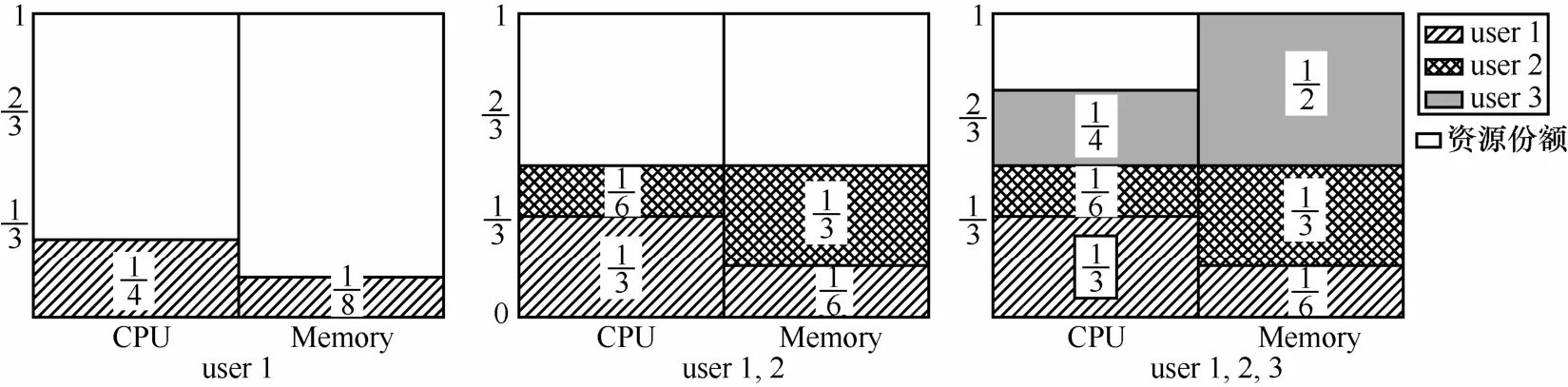

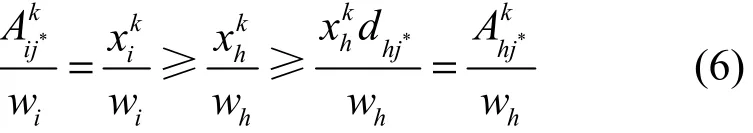
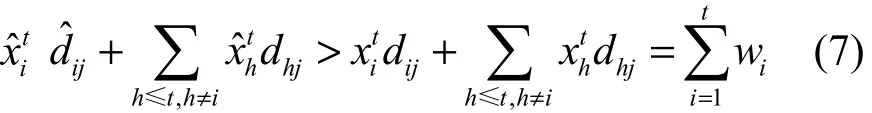
5 DMFA-SRQ算法
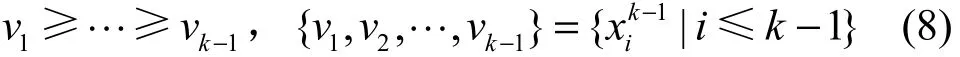


6 实验评估




7 结束语
(School of Information Science and Engineering, Yunnan University, Kunming 650091, China)




