基于能效最优准则的双跳中继网络功率分配算法

冀保峰，杨佳，王一丹，胡莹，李春国，宋梁,5

（1. 河南科技大学信息工程学院，河南 洛阳 471023；2. 东南大学毫米波国家重点实验室，江苏 南京 210096；3. 中国洛阳电子装备试验中心，河南 洛阳 471023；4. 江苏科技大学电子信息学院，江苏 镇江 212003；5. 多伦多大学，安大略 多伦多 M5S 2E8）

基于能效最优准则的双跳中继网络功率分配算法

冀保峰1,2，杨佳3，王一丹1，胡莹2,4，李春国2，宋梁1,5

（1. 河南科技大学信息工程学院，河南 洛阳 471023；2. 东南大学毫米波国家重点实验室，江苏 南京 210096；3. 中国洛阳电子装备试验中心，河南 洛阳 471023；4. 江苏科技大学电子信息学院，江苏 镇江 212003；5. 多伦多大学，安大略 多伦多 M5S 2E8）

针对单天线多跳系统中的资源分配策略进行了研究，重点研究了基于能效最优的功率分配算法。所提算法以系统能效最大化为设计目标，以满足指定的系统服务质量(QoS, quality of service)为约束条件，建立了以源节点和中继节点发射功率为设计变量的数学优化模型。通过大信噪比区间近似等效，将原始的非凸优化问题转化为凸优化问题。再利用拉格朗日对偶函数凸优化算法，并借助于LambertW函数，最终得到一种功率分配方案的闭合形式解，避免了采用交替迭代方法来求解最优化问题。相比传统以系统频谱效率最大化为目标的算法，所提算法能更好地提升系统整体能效，同时降低了功率分配算法的复杂度。

能效；资源分配；凸优化

1 引言

近年来，多跳无线通信技术得到了充分的发展。它利用中继辅助转发信源信号，使蜂窝系统在链路可靠性、小区覆盖范围以及系统频谱效率等方面取得了显著提升，也使其成为无线通信领域中的研究热点之一。特别是中继系统不需要昂贵的有线回程链路作为支撑，大幅降低网络部署及运营成本开销[1～6]。因此，中继辅助转发的多跳通信技术也被业内普遍认为是未来异构无线通信网络中的重要组成部分。

关于多跳网络系统性能的研究，诸多文献更多关注于系统频谱效率[7,8]和误码分析[9～14]的研究，然而，随着社会对通信系统要求的提高，特别是整个通信系统的功率消耗对人类生存、健康及环境所带来的问题越来越受到关注。由此，业界提出了以追求高能效为目标的绿色通信概念[15～19]，而功率分配问题则直接影响到整个系统的能效性能[20]。

Xu等[21]以正交频分复用(OFDM)多址系统为背景，考虑符号数和导频数，并基于能效最大化的目标函数获得最优的功率分配。He等[22]在分布式天线系统中基于能效最大化的目标函数获得了最优的功率分配方案。中继辅助转发网络下，将利用博弈论设计的最优功率分配策略应用于 CDMA网络中得到了较深入的研究[23]，而假定固定增益的中继系统下，以最小化功率为准则，Zafar等[24]设计了最优的功率分配方案。

然而，系统的总功率消耗不单包括发射机的实际发射功率，也包括维持设备运转时的电路功耗。在传统中继辅助系统的功率分配方案中，多以系统频谱效率最大化为目标，在忽略电路功耗的前提下，以提升发射功率来获得系统频谱效率的最大化，在此情况下，会造成系统整体能效性能非常低。

为了使中继系统能满足未来绿色通信对系统能量效率(能效)的要求，在系统设计方面引入能效作为优化准则，并考虑系统的QoS要求，从而在保证系统传输有效性的同时，尽可能提升系统的能效性能。同时，考虑中继节点与信源节点发射功率联合优化。由于目标函数的复杂性，目前还没有很好的低复杂度联合功率分配解决方案，对于最优功率分配方案的闭合形式解更是难以获得。

本文提出了一种基于能效最大化的单天线两跳中继系统联合功率分配设计算法。该算法以系统能效最大化为设计目标，以满足指定的系统服务质量(QoS, quality of service)为约束条件，建立了以源节点和中继节点发射功率为设计变量的数学优化模型。通过大信噪比区间近似等效，将原始的非凸优化问题转化为凸优化问题。再利用拉格朗日对偶函数凸优化算法，并借助LambertW函数[25]，最终得到一种低复杂度的功率分配方案的闭合形式解，避免了采用交替迭代方法来求解最优化问题。

2 系统模型

本文所研究的通信系统由一个信源节点、一个信宿节点和一个放大转发中继节点所组成，且3个节点均配置为单天线，暂不考虑同信道干扰。假定所有节点使用同一个频带，且源节点和目的节点之间无直达径，系统模型如图1所示。

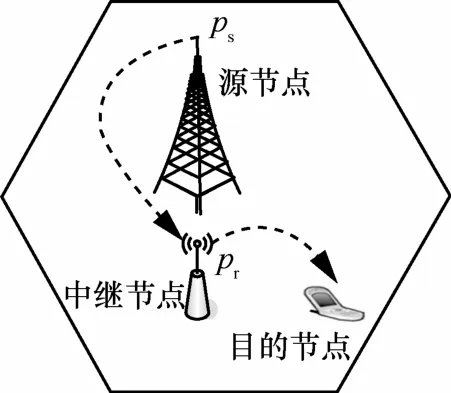
图1 系统模型示意

第一个时隙内，信源节点发送信号x（x为功率归一化信号）到中继节点，则中继节点接收的信号可以表示为

其中，ps是信源发射功率，h是信源节点至中继节点的无线信道，服从循环对称复高斯分布，即CN (0,1)，n1是均值为零、方差为1的加性高斯白噪声(AWGN)，则目的节点接收到的信号可以表示为

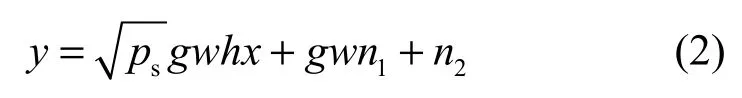
其中，n2是中继节点至信宿节点的均值为零、方差为1的加性高斯白噪声。g为中继节点至信宿节点的无线信道，服从循环对称复高斯分布，即CN (0,1)，w是中继节点所带来的增益，可表示为

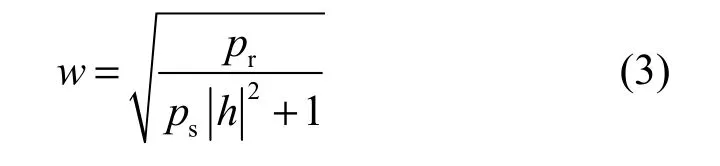
其中，pr是中继节点的发射功率。因此，信宿节点的信噪比可以表示为

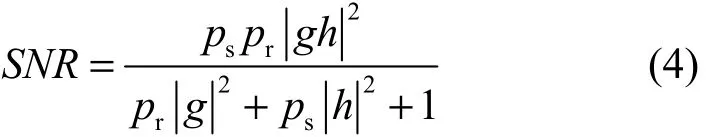
从而，可以得到瞬时的系统频谱效率(SE,spectral efficiency)为

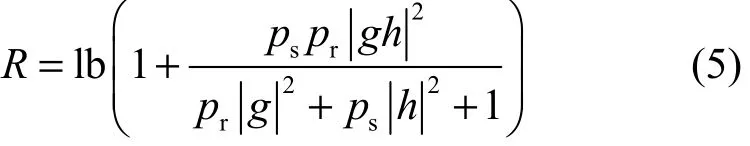
一般来讲，由于系统是2个时隙的信息交互，该频谱效率R的对数函数前应乘以因子，然而，该因子并不影响本文基于能效最优的功率分配算法设计，故暂忽略该因子。本文假定中继节点已知两跳信道状态信息g和h，信源节点可以通过中继节点的反馈进行功率分配算法的设计。

基于能效最优的绿色通信系统的功率消耗主要包括发射功率、电路消耗、转换效率消耗以及冷却消耗等，因此，信源节点和中继节点的总功率消耗可以表示为

本文的功率消耗模型参数[ai, bi] (i = 1,2)是基于EARTH 计划的实际参数设置的[26]，整个系统的总功率消耗可以表示为

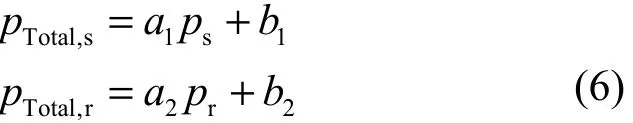
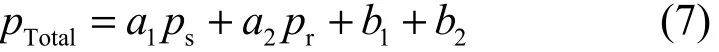
因此，本文所研究的系统能量效率可以定义为系统频谱效率除以总的功率消耗，其单位为bit/(s·Hz·J)，可以表示为

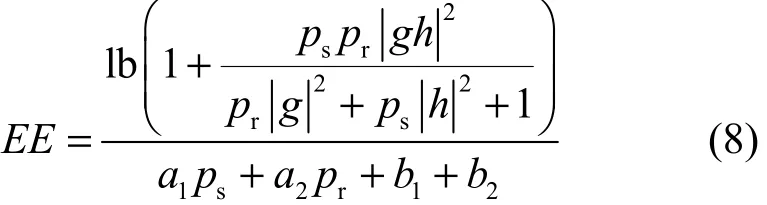
式(8)是本文研究的绿色通信通信系统的重要表达式，其物理意义在于它是每个比特信息从信源节点通过中继节点传输至信宿节点的频谱效率测度，该测度不同于传统形式的频谱效率表达式[27]，例如Xu等在文献[28]中也定义了相似的测度，而本文所提的能效测度表达式能够更加有效地评估能效通信系统，同时也需要解决该中继能效通信系统的一些问题。

3 联合信源中继节点的能效最优的多跳系统功率分配

本文在保证所需最小频谱效率的目标下通过对发送功率ps和pr的最优分配以获得系统能效的最大化，本部分首先利用式(8)的定义建立联合信源和中继节点的优化模型，通过利用Lagrangian乘子等方法获得该优化问题由非凸向凸的转化，其中本文利用了Lambert函数以及它的性质来简化并解决复杂的优化问题。

3.1 问题形成

本节首先给出在系统最小频谱效率的约束条件下最大化能效的数学问题，可表示为

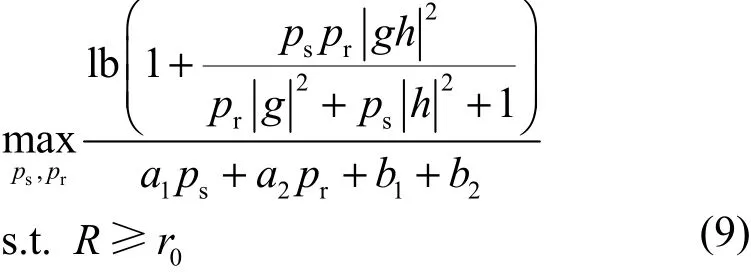
其中，r0是所需的最小频谱效率，单位为bit/(s·Hz·J)，需要说明的是用户端服务质量的约束可以有不同的表示形式。式(9)中 R≥r0即为最小频谱效率约束，结合目标函数和约束条件并通过海森矩阵计算可以得出该数学问题是非凸问题，这是由于目标函数中信噪比的表达式分母中含有常数1导致的。在文献[29]已证明了如果忽略常数1，则该数学问题是凸问题，而且 Boyd等已经在文献[30]中证明凸函数的仿射函数一定是伪凸函数，因此，通过高信噪比的近似，式(9)中的数学问题可以转化为如下的伪凸优化问题

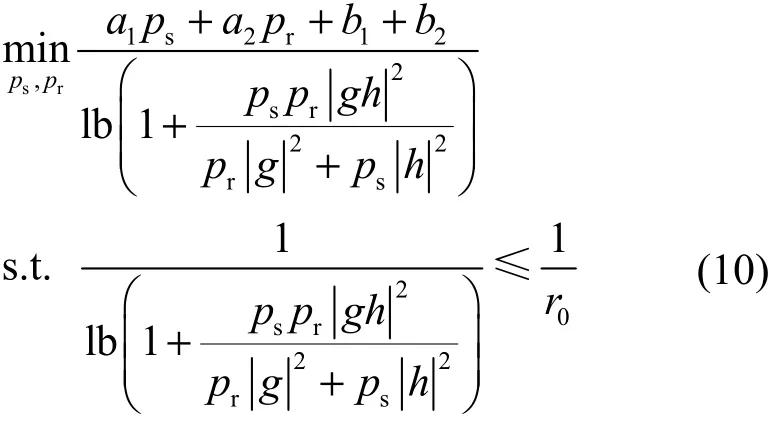
该近似的原理主要是源于实际中2个噪声方差的乘积通常远远小于高发射功率下ps和pr之积。

3.2 解析表达式的推导

式(10)对应的拉格朗日函数可以表达为[31,32]

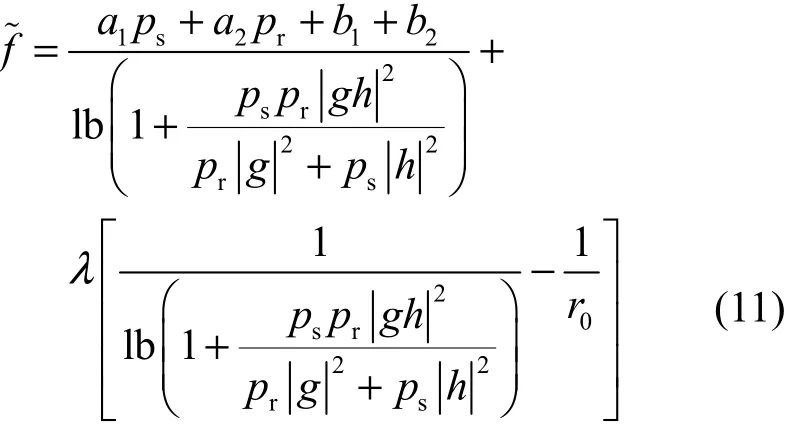
由凸优化理论的KKT条件可以获知，拉格朗日函数f˜关于变量ps和pr的一阶导数应为零，且拉格朗日乘子λ≥0。因此，通过求解拉格朗日函数f˜关于变量ps和pr的一阶导数为零的方程可以得到

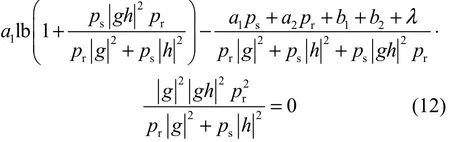
和

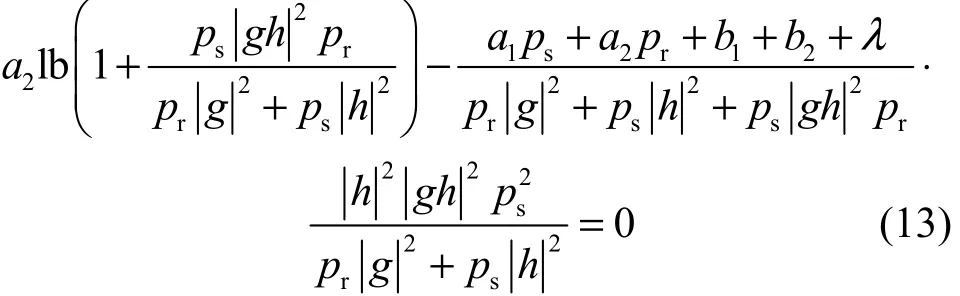
从式(12)和式(13)可以获得

通过对式(13)中pr的变量替换可以得到

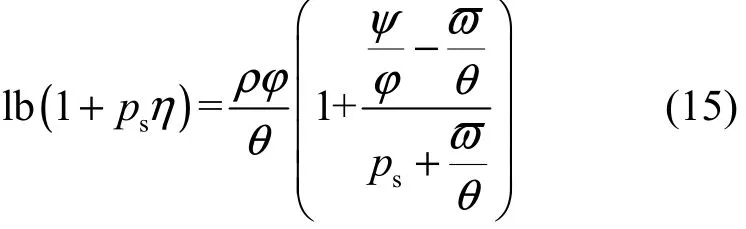
其中，

需要说明的是对于方程(15)的求解是比较困难的，其难点主要在于方程左边是对数函数，而方程右边是线性函数，无法线性求解。为了求解方程(15)，本文引入了Lambert函数，该函数是 zez的逆函数。例如，若 φ= zez，则可得到 z=W{ φ}[25]。本

文定义

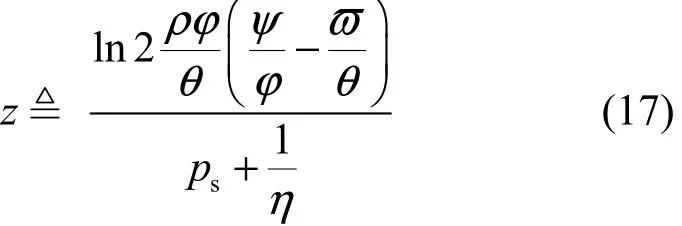
则方程(15)可转换为

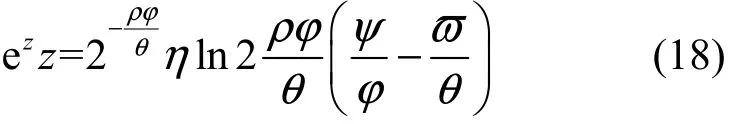
关于变量z的方程(18)可通过 Lambert函数获得求解如下

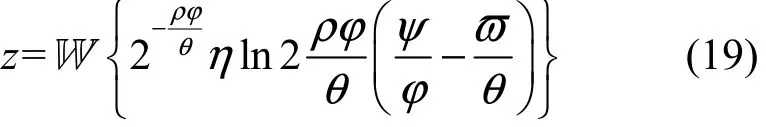
其中，W { ⋅}是Lambert函数，即对于方程 wew=ς中ς>0的变量而言，该方程关于w的解可通过Lambert函数W{ς}获得，从而ps的解可以表达为

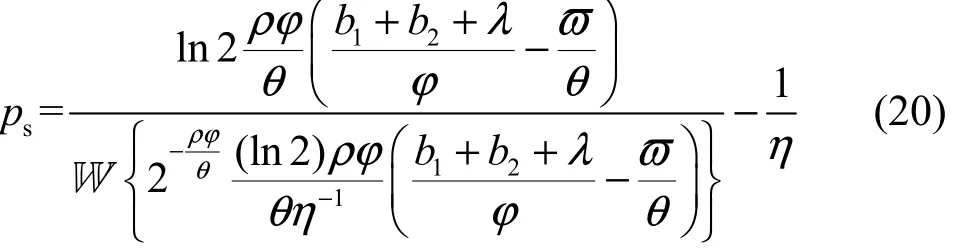
式(20)的推导结果中包含了拉格朗日乘子λ，而式(10)的KKT条件中要求拉格朗日乘子λ是非负的，该问题的求解可通过下面分情况的计算方法获得。

3.3 拉格朗日乘子的计算

由于拉格朗日乘子λ≥0，所以本节分2种情况进行讨论和求解。

1) 当λ>0时

本文首先研究λ>0的情况，式(10)的其中一个KKT条件可以表示为

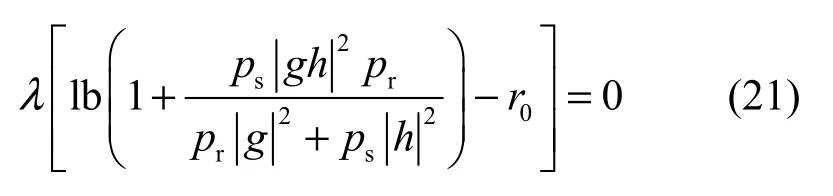
该式是指对于λ>0的情况时，式(10)的第二项等于零才能满足KKT条件，通过将式(14)和式(20)代入KKT条件，得到

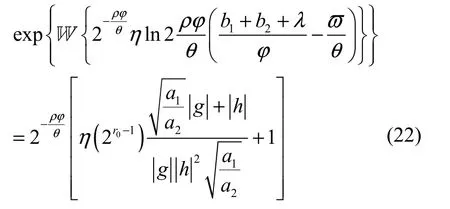
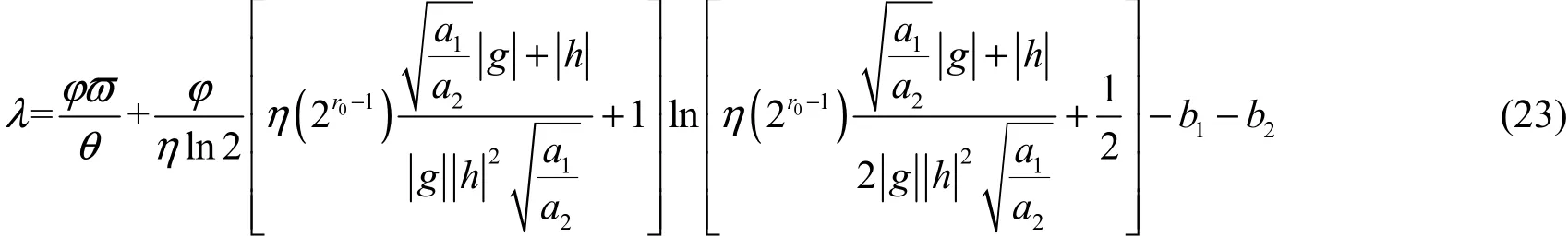
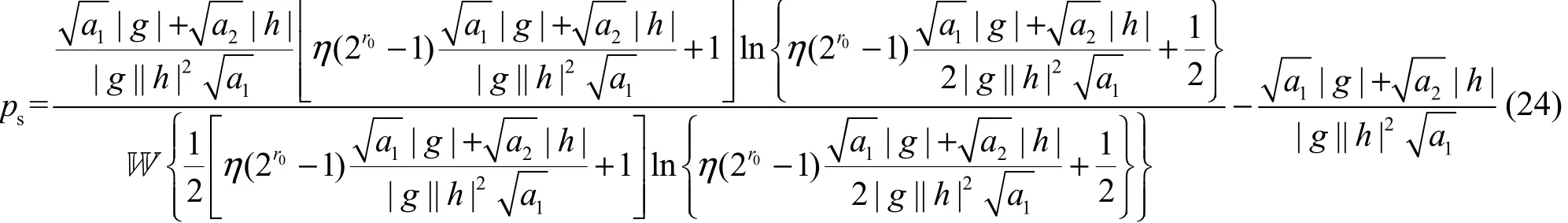
因此，通过将式(24)的结果代入式(14)中可以获得中继节点最优功率分配pr的表达式为

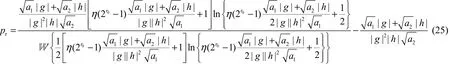
2) 当λ=0时

通过推导可以获得λ=0情况下的最优功率分配表达式，即通过求解可得

从而，最优发送功率ps可推导获得如式(27)所示。

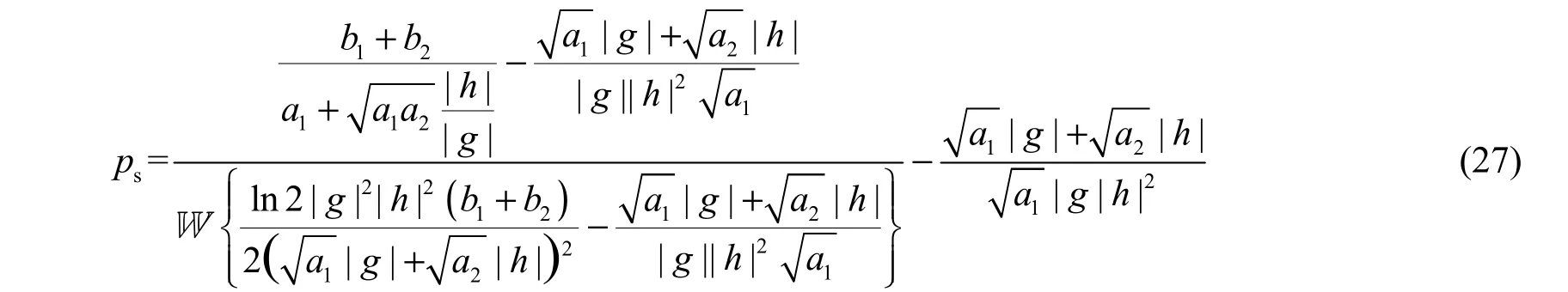
将式(27)代入式(14)可推导出中继节点pr的最优发送功率为

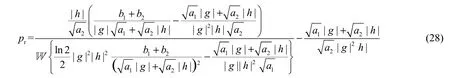
讨论 1 式(27)关于最优的发送功率ps并不能保证最小的频谱效率约束，若该情形出现，则实际应用中应舍掉式(27)而采用式(24)的结果，即将式(24)中关于ps的解作为最优的发送功率分解。另外，需说明的是式(24)和式(27)均为正确结果，而选择哪个表达式作为最优的发送功率分配取决于哪个结果能获得更高的能量效率。

讨论 2 式(28)关于最优的中继节点功率分配是两跳单中继通信系统的能效研究，而且，联合信源中继节点最优功率分配的能效研究可扩展至多跳多中继通信系统中[31]。以多跳多中继系统为例，信源节点和多个中继节点的功率分配均可通过本文定义的最大化能效表达式来获得最优功率分配，然而，该问题的求解将引入高阶变量的推导，这方面的推导和性能分析的研究将作为基于能效最大化的最优功率分配的后续工作进行展开。

讨论 3 由于本文所提方案主要关注单用户发送，下面讨论如何将本文所提单用户发送方案扩展至多用户场景，并且不需要额外的公式推导，值得一提的是多用户的扩展最大的问题是用户间的干扰，本文给出2种解决方案。

第 1种方案可以通过OFDMA(orthogonal frequency division multiple access)技术消除多用户之间的干扰，多用户的发送可以通过将本文发送方案应用不同频率，因而，正交的频分复用多址技术使多用户之间完全正交，多用户之间的干扰也可以完全消除。

第 2种方案可以通过 OFDM (orthogonal frequency division multiplexing)技术消除多用户之间的干扰，多用户的发送可以通过将本文发送方案应用于不同子载波上，因而，OFDM的正交子载波使不同用户间保持较好的正交性，所以多用户之间的干扰也可以完全消除。

讨论 4 本文所提方案是基于大信噪比情况下近似获得的，需要说明的是，中低信噪比情况下，所提方案是无法获得类似大信噪比的近似公式的，因而无法获得所提方案的闭合解析解，由于目标函数的分数形式，故只能通过蒙特卡洛获得其数值解。

4 仿真和分析

本节对所提出的联合信源中继节点功率分配以最大化能效的方案进行了仿真，其中蒙特卡洛仿真次数设为10 000，且功率消耗模型参数[a1, b1]和[a2, b2]设为[7 .25,469]、[3 .14,69]或[4 .4,8.7]。3种可能场景的选择，即宏基站(macro BS)、微基站(micro BS)和微微基站(pico BS)取决于EARTH计划中的建模[26]。基于频谱效率最大化的功率消耗场景和次优的方案也进行了仿真和分析，其中信源和中继节点的功率之比τ=可通过式(14)推导获得并且参考

WINNER计划取固定的值。需要说明的是本节在仿真中利用了Matlab软件中的W { ⋅}函数。

图2的功率消耗模型(PCM, power consumption model)参 数 仿 真 中 设 置 为 [a1, b1]= [3.14,69]和[a2, b2]= [4.4,8.7]，图2给出了所提方案与其他2种方案[35～37]的能效和所需最小频谱效率的对比结果，从图中可以看到r0=2bit/(s·Hz)时，所提方案比已有文献中的速率最大化方案高20%的增益，比功率比τ=的次优方案高30%的增益。

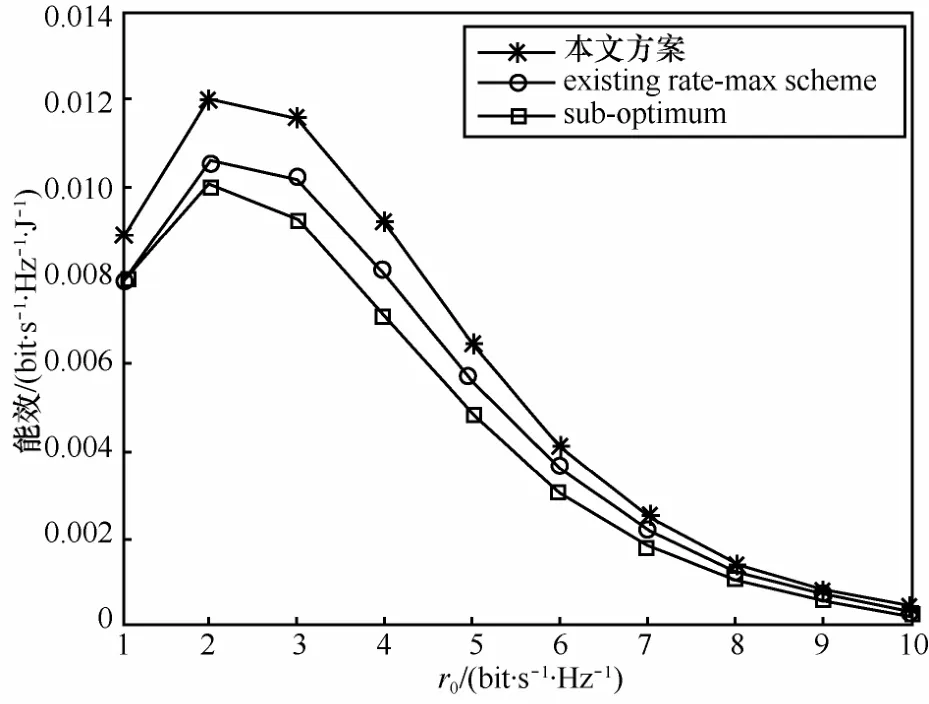
图2 所需频谱效率r0与能效对比结果

图3给出了不同功率消耗模型参数(PCM)下所提方案可获得的能量效率结果，从图中可以看到当PCM参数为 a= 7.25,b = 469的宏基站时，无论中继节点参数如何变化，能量效率会急剧恶化；而且，当信源节点或中继节点是宏基站时( a=7.25,b= 469)，所有能量效率曲线逐渐趋于相同。其中值得说明的是，EE先递增后递减主要是因为所需服务质量要求的增加所导致的，频谱效率的提升是以发送功率的增加为代价的，同时获得了一定的能效；然而，低频谱效率的方案中能效的增益要大于发送功率的代价。

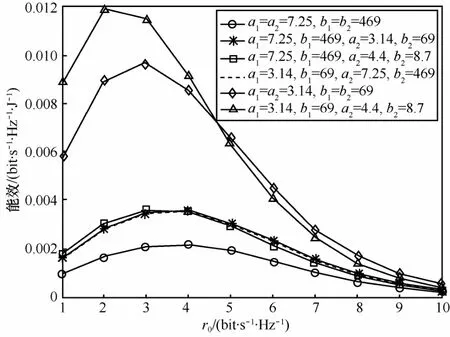
图3 不同PCM参数下的能效对比结果

5 结束语

本文针对两跳单信源单中继系统设计了一种基于能效最大化的联合信源中继节点的最优功率分配方案，建立了以源节点和中继节点发射功率为设计变量的数学优化模型，通过大信噪比区间近似的等效，将原始的非凸优化问题转化为凸优化问题。再利用拉格朗日对偶函数凸优化算法，并借助于LambertW函数，最终得到一种功率分配方案的闭合形式解，避免了采用交替迭代方法来求解最优化问题，相比传统以系统频谱效率最大化为目标的算法，本算法能够更好地提升系统整体能效，同时降低了功率分配算法的复杂度。通过仿真验证了所提方案的有效性和理论推导的正确性。另外，本文所研究的两跳中继系统向多跳系统的扩展将是该方向的后续工作。

[1] IKKI S S. Optimisation sudy of power allocation and relay location for amplify-and-forward systems over Nakagami-m fading channels[J].European Transactions on Emerging Telecommunications Technologies, 2012, 89(6)： 1110-1122.

[2] SUN F, KIM T M, PAULRAJ A J, et al. Cell-edge multi-user relaying with overhearing[J]. IEEE Communication Letters, 2013, 17(6)：1160-1163.

[3] ZENG W, ZHENG Y R, WANG M, et al. Linear precoding for relay networks： a perspective on finite-alphabet inputs[J]. IEEE Transations on Wireless Communications, 2012, 11(3)： 1146-1157.

[4] JI M, WANG Z, SADJADPOUR, H R, et al. The capacity of multihop relay wireless networks[C]//European Wireless Conference. c2010：49-56.

[5] ZENG W, XIAO C, WANG M, et al. Linear precoding for relay networks with finite-alphabet constraints[C]//IEEE International Conference on Communications. c2011： 1-5.

[6] LIU H, SUN F, DE CARVALHO E, et al. MIMO four-way relaying[C]//IEEE International Workshop on Signal Processing Advances for Wireless Communications (SPAWC). c2013： 46-50.

[7] SUN F, POPOVSKI P, THAI C, et al. Sum-rate maximization of coordinated direct and relay systems[C]//IEEE 18th European Wireless Conference (EW). c2012： 1-7.

[8] SUN F, DE CARVALHO E, THAI C D T, et al. Beamforming design for coordinated direct and relay systems[C]//IEEE 46th Annusal Conference on Information Sciences and Systems (CISS). c2012： 1-6.

[9] JIANG J, XIN Y, POOR V H. Achievable rates for discrete memoryless relay channels with generlised feedback[J]. European Transactions on Emerging Telecommunication Technologies, 2013, 24： 212-231.

[10] DAI M, WANG P, ZHANG S, et al. Survey on cooperative strategies for wireless relay channels[J]. European Transactions on Emerging Telecommunication Technologies, 2014, 25(9)：926-942.

[11] THOMSEN H, PRATAS NK, STEFANOVIC C, et al. Code-expanded ratio access protocol for M2M communications[J/OL].http：//kom.aau.dk/～petarp/papers/2013_wiley_ETT_M2M.pdf.

[12] DAI M, SUNG C W. Achieving high diversity and multiplexing gains in the aynchronous parallel relay network[J]. European Transactions on Emerging Telecommunication Technologies, 2013, 24： 232-243.

[13] SUN F, DE CARVALHO E, POPOVSKI P, et al. Coordinated direct and relay transmission with linear non-regenerative relay beamforming[J]. IEEE Signal Processing Letters, 2012, 19(10)： 680-683.

[14] ZHAI C, XU H, LIU J, et al. Performance of opportunistic relaying with truncated ARQ over Nakagami-m fading channels[J]. European Transactions on Emerging Telecommunication Technologies, 2012, 23：50-66.

[15] KARMOKAR A K, ANPALAGAN A. Energy-efficient cross layer design of dynamic rate and power allocation techniques for cognitive green radio networks[J]. European Transactions on Emerging Telecommunication Technologies, 2013, 24： 762-776.

[16] TANG X, PU J, GAO Y, et al. Energy efficient multicast routing scheme for wireless sensor networks[J]. European Transactions on Emerging Telecommunication Technologies, 2014, 25(10)： 965-980.

[17] ASHRAF M, SOHAIB S. Energy-efficient delay tolerant space time codes for asynchronous cooperative communications[J]. European Transactions on Emerging Telecommunication Technologies, 2014,25(12)：1231-1237.

[18] REVIRIEGO P, MAESTRO J A, HERNANDEZ J A, et al. Study of the potential energy savings in Ethernet by combining energy efficient Ethernet and adaptive link rate[J]. European Transactions on Emerging Telecommunication Technologies, 2012, 23： 227-233.

[19] EJAZ W, SHAH G A, UL HASAN N, et al. Energy and throughput efficient cooperative spectrum sensing in cognitive radio sensor networks[J]. European Transactions on Emerging Telecommunication Technologies, 2015, 26(7)：1019-1030.

[20] SUN C, CEN Y, YANG C. Energy efficient OFDM relay systems[J].IEEE Transactions on Communication, 2013,61(5)： 1797-1809.

[21] XU Z, LI G Y, YANG C, et al. Energy efficient power allocation for pilots in training-based downlink OFDMA systems[J]. IEEE Transactions on Communication, 2012, 60(10)： 3047-3058.

[22] HE C, SHENG B, ZHU P, et al. Energy efficiency and spectral efficiency tradeoff in downlink distributed antenna systems[J]. IEEE Wireless Communication Letters, 2012, 1(3)： 153-156.

[23] ZAPPONE A, BUZZI A, JORSWIECK E. Energy-efficient power control and receiver design in relay-assisted DS/CDMA wireless networks via game theory[J]. IEEE Communication Letters, 2011, 15(7)：701-703.

[24] ZAFAR A, RADAYDEH R D, CHEN Y, et al. Energy efficient power allocation for fixed-gain amplify-and forward relay networks with partial channel state information[J]. IEEE Wireless Communication Letters, 2012, 1(6)： 553-556.

[25] VALLURI S R, JEFFREY D J, CORLESS R M. Some applications of the Lambert W function to physics[J]. Canadian Journal of Physics,2000, 78(9)： 823-831.

[26] AUER G, et al. D2.3： energy efficiency analysis of the reference systems, areas of improvements and target breakdown[R]. INFSO-ICT-247733 EARTH (Energy Aware Radio and Network Technologies), 2010.

[27] SUN F, D E CARVALHO E. Degrees of freedom of asymmetrical multi-way relay networks[C]//IEEE International Workshop on Signal Processing Advances for Wireless Communications (SPAWC). c2011：531-535.

[28] XU Z, YANG C, LI G Y, et al. Energy-efficient configuration of spatial and frequency resources in MIMO-OFDMA systems[J]. IEEE Transactions on Communications, 2013, 61(2)： 564-575.

[29] LI C, WANG X, YANG L, et al. A joint source and relay power allocation scheme for a class of MIMO relay systems[J]. IEEE Transactions on Signal Processing, 2009, 57(12)： 4852-4860.

[30] BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge University Press, 2004.

[31] TANG X J, HUA Y B. Optimal design of non-regenerative MIMO wireless relays[J]. IEEE Transactions on Wireless Communications,2007, 6(4)： 1398-1407.

[32] LIU C H, VAIDYANATHAN P. MIMO broadcast DFE transceivers with QoS constraints： min-power and max-rate solutions[J]. IEEE Transactions on Signal Processoy, 2013, 61(22)：5550-5562.

[33] JI M, WANG Z, SADJADPOUR H R, et al. The capacity of ad hoc networks with heterogeneous traffic using cooperation[C]//IEEE INFOCOM. c2010： 1-9.

[34] TANG X J, HUA Y B. Optimal design of non-regenerative MIMO wireless relays[J]. IEEE Transactions on Wireless Communications,2007, 6(4)： 1398-1407.

[35] LIU C H, VAIDYANATHAN P. MIMO broadcast DFE transceivers with QoS constraints： min-power and max-rate solutions[J]. IEEE Transactions on Signal Processing, 2013, 61(22)：5550-5562.

[36] YANG L, MOHAMED S A. On the BER and capacity analysis of MIMO MRC systems with channel estimation error[C]//IEEE WiMob.c2011： 193-198.

[37] LIM Y G, CHAE C B, GIUSEPPE C. Performance analysis of massive MIMO for cell boundary users[J]. IEEE Transactions on Wireless Communications, 2015, 14(12)： 6827-6842.

Power allocation algorithms in two-hop relaying networks based on optimal energy efficiency

JI Bao-feng1,2, YANG Jia3, WANG Yi-dan1, HU Ying2,4, LI Chun-guo2, SONG Liang1,5
(1. College of Information Engineering, Henan University of Science and Technology, Luoyang 471023, China;2. School of Information Science and Engineering, Southeast University, Nanjing 210096, China;3. Luoyang Electronic Equipment Test Center, Luoyang 471023, China; 4. College of Information Engineering,Jiangsu University of Science and Technology, Zhenjiang 212003, China; 5. University of Toronto, Ontario M5S 2E8, Canada)

The joint source-relay power allocation issue in green dual-hop single antenna relaying systems was investigated from the energy efficiency point of view. By considering a practical power consumption model, the optimal algorithm in order to satisfy the constraints of system quality of service was proposed. The non-convex problem was converted into the convex problem through high power approximation and then the highly complicated optimization problem was solved by deliberately manipulating the Lagrangian function using the properties of the Lambert function. The optimal transmit power of the source and that of the relay are derived in the form of analytical expressions based on the maximization of EE with a guarantee of the required spectral efficiency (SE). It is shown that the optimal relay-to-source power ratio is adaptive to the ratio of the instantaneous two-hop channel gains. Numerical simulations have illustrated the effectiveness of proposed scheme.

energy efficiencey, resources allocation, convex optimization

s: The National Natural Science Foundation of China(No.U1404615, No.61201172, No.61201176, No.61372101),Open Funds of State Key Laboratory of Millimeter Waves(No.K201504), China Postdoctoral Science Foundation(No.2015M571637),The National Science and Technology Major Project of China (No.2013ZX03003006-002, No.2012ZX03004005-003), Foundation and Frontier Project of Natural Science Foundation of Henan Province (No.142300410343),Youth Foundation of Henan University of Science and Technology(No.2014QN030), Education and Teaching Reform Project(No.2015YB-033)

TN925

A

10.11959/j.issn.1000-436x.2016140

2015-06-24；

2016-04-26

冀保峰，baofengji@seu.edu.cn

国家自然科学基金资助项目（No.U1404615, No.61201172, No.61201176, No.61372101）；毫米波国家重点实验室开放课题基金资助项目（No.K201504）；中国博士后基金资助项目（No.2015M571637）；国家科技重大专项基金资助项目（No.2013ZX03003006-002, No.2012ZX03004005-003）；河南省自然科学基金基础与前沿基金资助项目（No.142300410343）；河南科技大学青年基金资助项目（No.2014QN030）；河南科技大学教育教学改革资助项目(No.2015YB-033)

冀保峰（1985-），男，河南洛阳人，河南科技大学讲师，主要研究方向为协作通信技术、中继网络、毫米波 MIMO、干扰管理等。

杨佳（1983-），男，江苏海州人，中国洛阳电子装备试验中心工程师，主要研究方向为通信网络对抗等。

王一丹（1992-），女，河南洛阳人，河南科技大学硕士生，主要研究方向为协同通信技术、毫米波MIMO等。

胡莹（1981-），女，江苏金坛人，东南大学博士后，江苏科技大学讲师，主要研究方向为MIMO通信信号处理、多用户信号处理和动态资源分配等。

李春国（1983-），男，山东胶州人，东南大学副教授，主要研究方向为中继网络、干扰协调、MIMO信号处理等。

宋梁（1980-），男，加拿大人，加拿大多伦多大学教授，主要研究方向为认知网络、低功耗网络、分布式计算。