单向证据冲突度量方法

王路，邢清华，毛艺帆

（空军工程大学防空反导学院，陕西 西安 710051）

单向证据冲突度量方法

王路，邢清华，毛艺帆

（空军工程大学防空反导学院，陕西 西安 710051）

针对传统证据冲突度量方法无法表达证据间支持程度差异的问题，提出一种带有方向性的证据冲突度量方法。该方法基于单向支持度间接计算证据间的冲突程度，单向支持度模型采用取小累加运算来表征两证据观点的一致程度，支持系数的引入保证了所建模型具有非对称性。实验结果表明所提方法不但能够有效区分证据间支持程度的差异，而且还能克服传统方法在特定情况下失效的问题。

Dempster-Shafer证据理论；方向；证据冲突；冲突度量

1 引言

证据理论由Dempster于1967年在研究统计问题时首次提出[1]，后经其学生Shafer推广和发展[2]，成为系统化的不确定性推理理论，故又名Dempster-Shafer（D-S）理论。D-S理论具有在无先验信息的条件下有效表达和处理不确定信息，并通过证据积累缩小假设集合的能力[3]，因而在数据融合[4]和决策分析[5]等领域得到广泛应用。

在D-S理论的实际应用中，受客观条件以及传感器自身性能的影响，证据之间往往高度冲突，此时采用D-S理论进行证据合成，往往会得到反直观结果。为解决这一问题，国内外大量外学者提出了改进方法，主要分为2类[6]：对组合规则的修改[7,8]和对证据源的修改[9]。但是无论何种方法，首先都需要确定证据之间是否存在冲突以及冲突程度大小，因而证据冲突度量方法成为关键。

现有证据冲突度量方法主要基于冲突系数[2]、Jousselme证据距离[10]、夹角余弦[11]、Pignistic概率距离[12]实现[13～20]。本文通过实例分析发现，采用冲突系数对完全相同的证据进行度量时，计算结果却不为零，即存在冲突；采用证据距离对完全不同的证据进行度量时，结果却不都为理论最大值 1，并且其大小还随着基本概率赋值（BPA, basic probability assignment）分散程度的不同而改变；而余弦相似度在处理证据中包含非单子集焦元时不够准确；Pignistic概率距离对不完全一致的2个证据进行度量，结果却可能为1。

此外，典型冲突度量方法都具有对称性，因而无法表达证据间相互支持程度的差异，针对此问题，文献[21]基于Jousselme证据距离设计了非对称证据冲突度量方法，但是并没有解决证据距离失效的问题。

为解决现有冲突度量方法无法表达证据间相互支持程度的差异，并且会在特定情况下失效的问题，本文提出了一种新的证据冲突度量方法，实验结果验证了所提方法的有效性。

2 D-S理论

设Θ为待判决命题的所有可能答案构成的完备集合，Θ中元素两两互斥，则称此互不相融事件的完备集合Θ为识别框架[22]，记为Θ ={θ1,… , θN}。识别框架所有子集组成的集合称为Θ的幂集，用2Θ表示，其元素个数为。在识别框架的基础上，证据理论定义了重要的基本概率指派函数，并制定了证据组合规则。

定义1 （基本概率指派）设Θ为一识别框架，A为Θ的子集，若映射m： 2Θ→ [0 ,1]满足且 m(∅ )= 0，则称m为Θ上的基本概率指派函数。信任函数Bel和似真函数Pl定义为

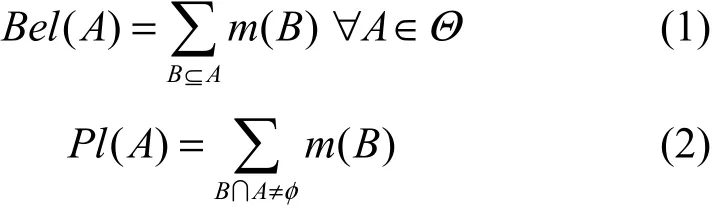
对于命题A，区间[B el( A), P l( A) ]构成信度区间，用于表示A发生的可能性，其中，Bel( A)表示对A的支持度的下界，Pl( A)表示对A支持度的上界，差值 Pl( A) −Bel( A)表示对A的不确定程度。

D-S理论证据组合规则为

3 典型冲突度量方法分析

3.1 冲突系数

经典证据理论用k来表征证据间的冲突程度，其物理意义为分配给空集的概率指派，k值越大，冲突程度越大。由k的计算公式可以看出，冲突系数具有对称性，即 k(m2) = k( m2, m1)，因此无法区分证据间相互支持程度的差异。

此外，冲突系数在使用时会出现失效的情况，即使完全相同的2条证据，其冲突系数大小也并非期望值零，如例1所示。

例 1 假设识别框架Θ ={θ1,θ2}，两完全相同的证据体为

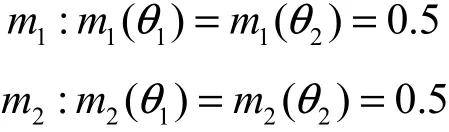
计算结果为k=0.5，与事实不符，可见，传统冲突系数无法有效表征证据间的冲突程度。

3.2 Jousselme证据距离

证据距离由 Jousselme提出，原意是用来衡量一组代表分类结果的证据与一组表示真实解的证据之间的差异性[23]，其定义如下。

定义2 （Jousselme证据距离）假设识别框架为Θ，两证据体的BPA为m1、m2，其矢量形式为m1、m2，则两证据的Jousselme证据距离[10]为

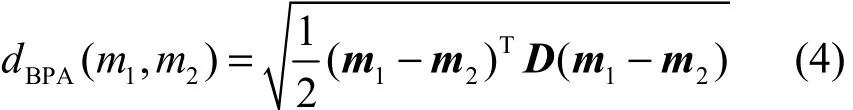
其中，D为2N2N× 矩阵，矩阵中元素

由定义可以看出，证据距离同样具有对称性。而其失效的情况如例2所示。

计算结果为：对于情形1， dBPA= 0.707；对于情形2， dBPA= 0.577。可见即使完全不同的2个证据，其证据距离也并非理论最大值 1，并且其大小还与证据体的 BPA分散程度有关，BPA越分散，证据距离越小，这与逻辑分析结果相悖。

3.3 夹角余弦

定义3 （夹角余弦）设识别框架Θ ={θ1,…, θN}，两证据体的BPA为m1、m2，其矢量形式为m1、m2，则两证据的夹角余弦[11]为

其中表示向量的模。

相对证据距离，证据向量夹角余弦更加注重两证据在方向上的相似程度，在具体冲突程度数值的度量上不如其他方法准确，如例3所示。

例3 假设识别框架Θ = {θ1,θ2,θ3}下两证据体的BPA为

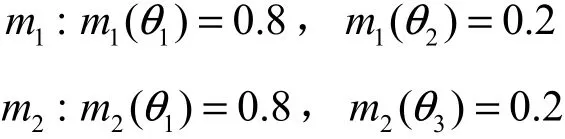
由两证据体的BPA可见，两证据有0.8的意见是一致的，其余0.2完全冲突，因此，证据相似度不应大于 0.8，但是两证据的夹角余弦计算结果为c(m2) = 0.94，与分析结果不一致，相比而言，证据距离的计算结果为 dBPA= 0.2，与事实相符。可见，相比证据距离，夹角余弦的测量精度不够准确。

此外，文献[13]指出夹角余弦模型并不适合证据中包含非单子集焦元情况，并给出了夹角余弦修正模型如下

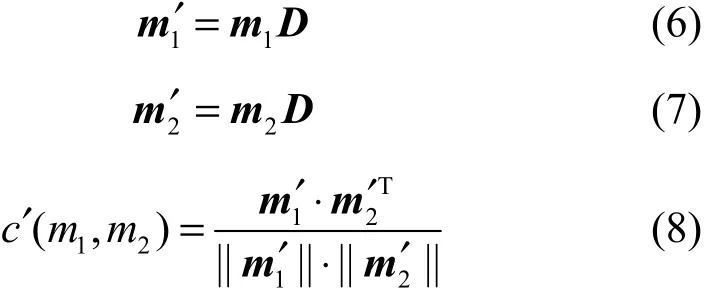
通过分析，修正模型同样存在问题。由于式(8)首先将证据体m1与矩阵D结合，直接导致生成了新的证据体相对原始证据体，增加了多余的信息，最终导致度量结果不够准确，如例4所示。

例 4 假设识别框架Θ ={θ1,θ2}下 2条证据的BPA为

根据式(6)～式(8)可得 c′( m1,m2) = 0.2，表明两证据不完全冲突，与事实不符。

3.4 Pignistic概率距离

定义 4 （Pignistic概率距离）设识别框架Θ= {θ1,… ,θN}，两证据体的BPA为m1、m2，则两证据体的Pignistic概率距离为

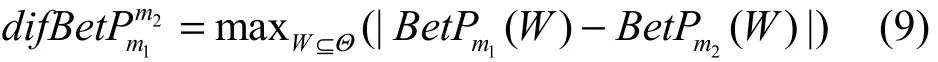
Pignistic概率距离在对2个不同的证据进行度量时会出现如例5所示问题。

例 5 假设识别框架Θ ={θ1,θ2}，两证据体的BPA如下。

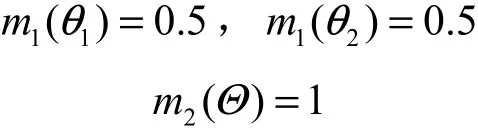
通过计算，两证据的 Pignistic概论距离difBe= 0，表明两证据没有任何冲突，完全一样，这与事实不符。此外，第4节仿真结果同样表明，Pignistic概率距离在进行冲突度量时不够准确。

4 单向冲突度量方法

通过对传统冲突度量方法的分析可以发现，传统冲突度量公式都具有对称性，即证据1对证据2的不支持程度与证据 2对证据 1的不支持程度相等，但真实的情况是：不确定度小的证据对不确定度大的证据的支持程度应该大于不确定度大的证据对不确定度小的证据的支持程度，如例6所示。

例 6 假设识别框架Θ ={θ1,θ2}，两证据体的BPA如下。

根据式(1)和式(2)可得，证据1中θ1的信度区间为[1,1]，θ2的信度区间为[0,0]，即证据1完全支持θ1，完全否定θ2；证据2中θ1的信度区间为[0,1]，θ2的信度区间同样为[0,1]，即对于命题θ1和θ2，证据2都完全不确定。此外，根据逻辑分析同样容易发现：证据1的不确定度要小于证据2的不确定度。在此，对两证据相互支持程度的差异进行分析。

证据1的完全表达为： m1(θ1)=1， m1(θ2)=0，m1(Θ ) = 0，由于 m1(Θ) = 0，因此证据 1不存在不确定性，其基本概率赋值为贝叶斯BPA，将其从幂集空间投影到概率空间后，其概率分布为p1(θ1) =1、 p1(θ2)=0，又因为θ1与θ2互斥，可得再将p1(Θ)转化到幂集空间，可得 m1′(Θ) = 1，即证据1通过转化可以得到证据2；但是证据2无法通过转化得到证据1，可见证据1对证据2的支持程度应该更大，即不确定度低的证据应该更加支持不确定度高的证据。

定义5 （单向支持度）设识别框架为Θ ={θ1,… ,θN}，两证据体的BPA为m1、m2，则证据1对证据2的单向支持度计算式为

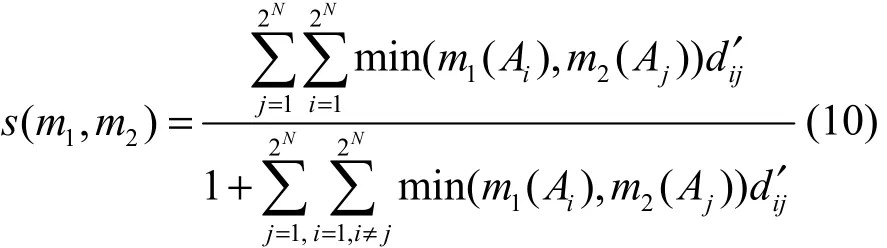
其中，dij′为支持系数，表示命题iA对命题Aj的支持程度，计算式为

证据单向支持度满足以下3条准则：

上述 3条准则的证明较为简单，在此做简要论述。对于准则1)，令则式(10)中分子可写为因此只需证又 由 式(8)可 知= 1， 并 且显然成立，准则 1)证毕；对于准则 2)，当可得又因为可得 m1=m2，准则 2)的必要性易证，在此省略；准则3)的充分性证明：由于 s( m1m2) = 0，可得式(10)分子为零，可得对于任意命题，可得 s( i, j) di′j= 0，即证据 1与证据 2无相交不为空的焦元，即(∪ Ai) ∩(∪ Bj)=∅ ，必要性易证，在此省略。

在证据支持度定义的基础上，证据1对证据2的不支持度，即证据1对证据2产生的冲突大小可通过公式 1 − s( m1m2)得到。

5 算例分析

实验 1 主要用于验证该方法能够克服传统方法在某些情况下失效的问题。

对 于 例 1， 计 算 结 果 为 1 − s( m1, m2) = 0，1 − s( m2, m1) = 0，表明两证据无冲突，与事实相符。

对于例 2，不同情形下的计算结果同为1 − s( m1, m2) =1 − s( m2, m1) = 1，表明两证据完全冲突，且都达到期望的理论最大冲突值1，与事实相符。

对 于 例 3， 计 算 结 果 为 s( m1, m2) = 0.8，s( m2, m1) = 0.8，与证据距离计算结果一致。

对 于 例 4， 计 算 结 果 为 s( m1, m2) = 0.4，s( m2, m1) = 0.333，表明两证据是有区别的，与分析结果一致。

对于例 5，计算结果为 s( m1, m2) =0，s( m2,m1) = 0，表明两证据完全冲突，与分析结果一致。

可见，所提方法能够有效克服传统方法在某些情况下失效的问题。

实验 2 主要用于验证所提方法能够有效区分证据间相互支持程度的差异。

假设识别框架Θ = {θ1,θ2,… ,θ20}，两证据体的BPA为 m1(θ2∪θ3∪θ4)=0.05，m1(θ7)=0.1，m1(Θ)=0.05， m1(Α) = 0.8； m2(θ1∪θ2∪θ3∪θ4∪ θ5)=1，命题Α按{θ1}，{θ1∪θ2}，{θ1∪θ2∪θ3}，…，{θ1∪ θ2∪…∪ θ20}的规律变化。图1给出了使用不同的证据冲突度量方法，两证据的冲突程度大小随的变化情况。

由图1所示结果可以看出，冲突系数的值恒为0.1，无法反映的变化对两证据冲突程度的影响；1 − c′ 、dBPA、1 −s( m1, m2)、1 − s( m2, m1)、difBetP的变化趋势一致，c′为式(8)所表示的修正夹角余弦，由于1 − c′提前对进行预处理，为证据增加了多余的信息，导致测量结果与事实不符，dBPA虽然能够区分两证据的冲突大小，但是无法区分谁对谁支持更多，Piginistic概率距离对=4与= 5的度量 结 果 一 致 ， 即 无 法 区 分{θ1∪θ2∪θ3∪ θ4}与{θ1∪ θ2∪ θ3∪ θ4∪ θ5}的区别，不够准确；相比而言， 1 −s( m1,m2)、1 − s( m2, m1)的变化趋势证据体现了证据之间支持程度的差异，在[1 ,5]的范围内，Α⊆ {θ1∪ θ2∪ θ3∪ θ4∪ θ5}，证据 1的不确定性更小，所以证据1对证据2的支持程度更大，从而证据1对证据2产生的冲突更小，此分析结果与图1所示一致，在[5 ,20]的范围内， {θ1∪ θ2∪ θ3∪ θ4∪θ5}⊆Α，证据2对证据1产生的冲突更小；当Α为 5时，Α与m2的焦元完全一致，证据间的冲突程度突然降为最低，并且变化幅度最大，这也充分说明了只有当 Α={θ1∪ θ2∪…∪ θ5}时，才可认为两证据对此命题的观点达成一致，而其他情况，即便Α与m2的焦元再接近，如{θ1∪ θ2∪ θ3∪ θ4}，都应认为其为2个不同的命题，可见，1−s的变化情况与逻辑分析更为一致。综上所述，本文所提算法不但能够解决传统度量方法存在的问题，而且能够准确、有效地表征证据之间的单向冲突程度。

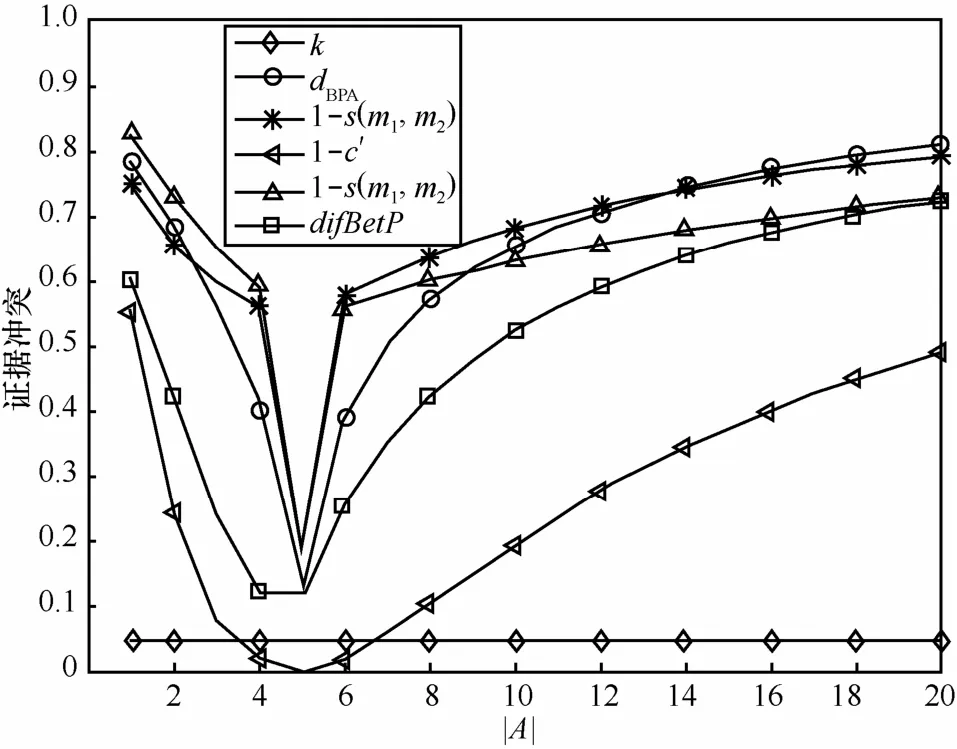
图1 不同方法下证据冲突大小随A变化情况

实验 3 主要用于验证所提证据冲突度量方法在代替传统冲突度量方法进行证据合成时是否能够得到较好的结果。

假设存在一多传感器构成的目标综合识别系统，空中待识别目标真实类型为θ1，识别框架Θ ={θ1,θ2,θ3}，4个相互独立传感器给出的证据如下

分别应用不同的组合方法对此例进行组合并对比分析，其中，本文证据合成方法流程与 Deng等[20]所提出的流程一致，只是将其所使用的证据距离替换为本文所提冲突度量方法，结果如表1所示。

表1 不同方法融合结果比较

由表1所示结果可以看出，使用Dempster基本组合规则进行证据合成时，受0-1悖论的影响，证据组合结果都为 m(θ1) = 0，与事实不符；文献[20]的方法通过分析证据间的关系（计算证据距离），得到证据权重，当证据体m3出现后，其方法能够正确识别目标；本文所使用的证据合成方法沿用文献[20]方法的证据合成流程，只是在度量证据冲突时使用本文所提冲突度量方法代替了证据距离，从合成结果可以看出，当只有证据体m1与m2时，合成结果与文献[20]方法一致，当证据体m3出现后，本文方法以更快的收敛速度支持θ1，可见，本文证据冲突度量方法具有很好的实用性。

6 结束语

本文提出了一种新的证据冲突度量方法，该方法基于单向支持度间接计算证据间的冲突程度。实验结果表明，所提方法不但能够克服传统证据冲突度量方法（冲突系数、证据距离以及证据向量余弦相似度）会在某些情形下失效的问题，而且能够使证据冲突的度量具有方向性，即能够区分证据间谁更支持谁。

本文在仿真最后一部分对所提证据冲突度量方法在证据合成时的有效性进行了简单验证，基于本文所提证据冲突度量方法设计更加合理的证据组合方式将是下一步的重点研究方向。

[1] DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. Annual Mathematics and Statistics, 1967, 38(2)：325-339.

[2] SHAFER G A. Mathematical theory of evidence[M]. Princeton：Princeton University Press, 1976.

[3] 权文, 王晓丹, 王坚, 等. 一种基于局部冲突分配的 DST组合规则[J]. 电子学报, 2012, 40(9)： 1880-1884.QUAN W, WANG X D, WANG J, et al. New combination rule of DST based on local conflict distribution strategy[J]. Acta Electronica Sinica,2012, 40(9)： 1880-1884.

[4] 王文庆, 杨远玲, 杨春杰. 一种基于证据理论的数据融合算法[J].控制与决策, 2013, 28(9)： 1427-1430.WANG W Q, YANG Y L, YANG C J. A data fusion algorithm based on evidence theory[J]. Control and Decision, 2013, 28(9)：1427-1430.

[5] 韩德强, 杨艺, 韩崇昭. DS证据理论研究进展及相关问题探讨[J].控制与决策, 2014, 29(1)： 1-10.HAN D Q, YANG Y, HAN C Z. Advances in DS evidence theory and related discussions[J]. Control and Decision, 2014, 29(1)： 1-10.

[6] 郭华伟, 施文康, 邓勇, 等. 证据冲突：丢弃,发现或化解[J]. 系统工程与电子技术, 2007, 29(6)： 890-898.GUO H W, SHI W K, DENG Y, et al. Evidential conflict and its 3D strategy： discard, discover and disassemble [J]. Systems Engineering and Electornics, 2007, 29(6)： 890-898.

[7] 高社生, 倪龙强, 杨凯, 等. 一种新的基于局部冲突分配的证据合成规则[J]. 西北工业大学学报, 2009, 27(1)： 43-46.GAO S S, NI L Q, YANG K, et al. A new and better rule for combining sharply conflicting evidence[J]. Journal of Northwestern Polytechnical University, 2009, 27(1)： 43-46.

[8] HAN D Q, HAN C Z, YANG Y. A modified evidence combination approach based on ambiguity measure[C]//The 11th International Conference on Information Fusion. c2008： 1-6.

[9] 宋亚飞, 王晓丹, 雷蕾, 等. 基于信任度和虚假度的证据组合方法[J]. 通信学报, 2015, 36(5)： 98-103.SONG Y F, WANG X D, LEI L, et al. Evidence combination based on the degree of credibility and falsity[J]. Journal on Communications,2015, 36(5)： 98-103.

[10] JOUSSELME A L, GRENIER D, BOSSE E. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(1)：90-101.

[11] WEN C L, WANG Y C, XU X B. Fuzzy information fusion algorithm of fault diagnosis based on similarity measure of evidence[J]. Lecture Notes in Computer Science, 2008, 5264： 506-515.

[12] LIU W R. Analyzing the degree of conflict among belief functions[J].Artificial Intelligence, 2006, 170(11)： 909-924.

[13] 宋亚飞, 王晓丹, 雷蕾, 等. 基于相关系数的证据冲突度量方法[J].通信学报, 2014, 35(5)： 95-99.SONG Y F, WANG X D, LEI L, et al, Measurement of evidence conflict based on correlation coefficient[J]. Journal on Communications,2014, 35(5)： 95-99.

[14] 刘希亮, 陈桂明. 一种自适应冲突证据检验与合成方法[J]. 控制与决策, 2014, 29(5)： 929-932.LIU X L, CHEN G M. A self-adaptive conflicting evidence test and combination approach[J]. Control and Decision, 2014, 29(5)： 929-932.[15] ALEXANDER L A. Estimation of conflict and decreasing of ignorance in Dempster-Shafer theory[J]. Procedia Computer Science, 2013,17： 1113-1120.

[16] MARTIN A, JOUSSELME A L, OSSWALD C. Con fl ict measure for the discounting operationon belief functions[C]//The 11th International Conference on Information Fusion. c2008： 1-8.

[17] CHEN L Z, SHI W K, DEND Y, et al. A new fusion approach based on distance of evidences[J]. Journal of Zhejiang University - Science A,2005, 6(5)： 476-482.

[18] YANG Y, HAN C Z, HAN D Q. Discounted combination of unreliable evidence using degree of disagreement[J]. International Journal of Approximate Reasoning, 2013, 54(8)： 1197-1216.

[19] THIERRY D. Conjunctive and disjunctive combination of belief functions induced by nondistinct bodies of evidence[J]. Artificial Intelligence, 2008, 172(3)： 234-264.

[20] DENG Y, SHI W K, ZHU Z F, et al. Combining belief functions based on distance of evidence[J]. Decision Support Systems, 2004, 38(3)：489-493.

[21] 王万请, 赵拥军, 黄洁, 等. 一种非对称的证据冲突度量方法[J].控制与决策, 2014, 29(3)： 533-536.WANG W Q, ZHAO Y J, HUANG J, et al. An asymmetrical measure for evidence con fl ict[J]. Control and Decision, 2014, 29(3)： 533-536.

[22] 杨风暴, 王肖霞. D-S证据理论的冲突证据合成方法[M]. 北京： 国防工业出版社, 2010.YANG F B, WANG X X. Combination method of conflictive evidences in D-S evidence theory[M]. Beijing： National Defense industry Press, 2010.

[23] 彭颖, 胡增辉, 沈怀荣. 一种修正证据距离[J]. 电子与信息学报,2013, 35(7)： 1624-1629.PENG Y, HU Z H, SHEN H R. A modified distance of evidence[J].Journal of Electronics & Information Technology, 2013, 35(7)：1624-1629.

Directional evidence conflict measurement approach

WANG Lu, XING Qing-hua, MAO Yi-fan
(School of Air and Missile Defense, Air Force Engineering University, Xi’an 710051, China)

Aiming at the problem that traditional evidence conflict measurement approaches can not express the difference of mutual support degrees between evidences, a directional evidence conflict measurement approach was proposed.The conflict degree of evidences could be measured based on the new defined directional support degree, which imported the support coefficient to make the model dissymmetrical. Simulation results show that the proposed method can not only express the difference of mutual support degrees between evidences, but also solves the problem that traditional approaches work poorly under special situation.

Dempster-Shafer evidence theory, direction, evidence conflict, conflict measure?

The National Natural Science Foundation of China (No.61272011)

TP391

A

10.11959/j.issn.1000-436x.2016143

2015-11-23；

2016-06-08

国家自然科学基金资助项目(No.61272011)

王路（1987-），男，陕西三原人，空军工程大学博士生，主要研究方向为高超声速飞行器防御关键问题。

邢清华（1966-），女，山西文水人，空军工程大学教授、博士生导师，主要研究方向为防空反导作战建模与仿真。

毛艺帆（1988-），女，陕西三原人，空军工程大学博士生，主要研究方向为反导预警多源信息融合。