一类三焦点曲线

高满屯， 李 阳， 王淑侠， 王守霞

(西北工业大学机电学院，陕西 西安 710072)

一类三焦点曲线

高满屯， 李 阳， 王淑侠， 王守霞

(西北工业大学机电学院，陕西 西安 710072)

针对三焦点曲线进行研究。首先提出一类三焦点曲线的概念和数学表达式，对该类三焦点曲线表达式的性质进行分析。其次，通过变化三焦点曲线参数，用计算机编程方法对三焦点曲线进行定量化分析和形状分析，分析和总结得到了曲线性质和规律。最后，通过对实际物体图像进行处理、提取边缘、曲线拟合等图像处理方法获得物体图像的三焦点曲线表示，并对实验结果进行了误差分析。实验结果表明三焦点曲线能够精确表示某些自然物体图像的轮廓。

三焦点曲线；自然物体；图像处理；曲线拟合；误差分析

物体(包括三维和二维物体)的表示是计算机视觉和图形学中最基本的问题，是对物体进行描述、分析、设计、制造、检测、识别、匹配和检索的理论基础。

在计算机图形学中，可以用各种各样的参数方程(如有理B样条等)表示物体的曲线曲面，虽然这样的表示法对灵活设计、分析曲线曲面具有很大的方便和优点，但其不具有唯一性，即同一条曲线可以用不同的参数方程予以表示，同一条曲线分段的节点不同，其表示方程也不同；这样的表示法是局部的，如有理 B样条所具有的局部性使得工程设计更加方便、灵活，但是在物体的识别、匹配和检索中难以使用，给实用工作带来了困难，需探索新的曲线表示方法。三焦点曲线曲面是一种很好的方法。

自然界很多物体可用三焦点曲线曲面来进行

唯一、整体的表示，比如天体及其运行轨迹、动物器官、细胞、植物果实等。圆是具有唯一焦点的曲线，椭圆和双曲线是具有两个焦点的曲线，人们对其的定义、几何性质、物理意义及其成因已有非常丰富的认识。但人们对三焦点曲线曲面尚未见相关研究报道。

文献[1]提出一种特殊的多焦点圆概念，该文实际上是采用多段圆弧连续拼接来表示椭圆和卵圆，并没有多焦点曲线的本质意义。物体轮廓线的表示、识别、匹配和检索是计算机视觉中的一个重要问题[2]。文献[3]提出一种物体特征曲线的识别方法，其采用B样条表示和进行匹配，特征集为曲率和挠率；文献[4]提出二维物体轮廓线用B样条曲线进行表示和匹配以识别二维物体。在计算机辅助几何设计中有些学者研究了隐式的曲线曲面表示方法[5-8]。

1 三焦点曲线定义和公式

三焦点曲线定义：三焦点曲线是到3个焦点的加权距离之和等于定长点的集合。

其数学表达式为

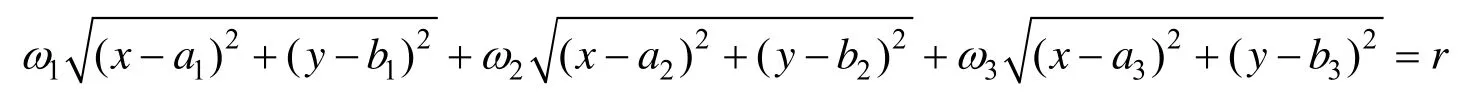
其中，(a1,b1),(a2,b2),(a3,b3)为3个焦点的坐标，r表示定长(正实数)，ω1, ω2,ω3为权重(实数)。为了方便表述，将权重为正值的焦点称为正焦点，将权重为负值的焦点称为负焦点。将焦点(a1,b1),···,(a3,b3)依次连接构成一个三边形，称为焦点三边形。

三焦点曲线的焦点构成的图形形状有多种可能性，如正三角形、等腰三角形、一般三角形、一条直线、其中的两个焦点重合等多种情况。三焦点曲线的形状是由焦点构成的三边形形状及其大小、定长长度和权重所决定的。

为了分析三焦点曲线形状和性质，本文通过量化焦点坐标、定长和权重参数，绘制曲线图形的方式，获得不同情况下的三焦点曲线。并对得到的可视曲线图形进行研究，分析三焦点曲线的规律。

2 焦点曲线定量分析

研究三焦点曲线采用的量化方法与研究超二次曲线的方法类似，即通过改变三焦点曲线公式中的不同参数，包括焦点位置(坐标)、定长参数 r和权重，得到不同的三焦点曲线，并分析总结三焦点曲线的形状及其性质。对参数进行有规律的定量化改变，最终对得到的曲线形状、规律及其变化趋势进行分析。通过软件标记焦点的坐标，控制参数变化，绘制图形。

2.1 焦点三边形为正三角形

以焦点三边形为正三角形为例，实验结果如下。

(1) 无负焦点时，限定定长和权重值，正三角形的边不断增大，观察三焦点曲线形态的变化情况。三焦点曲线的公式为

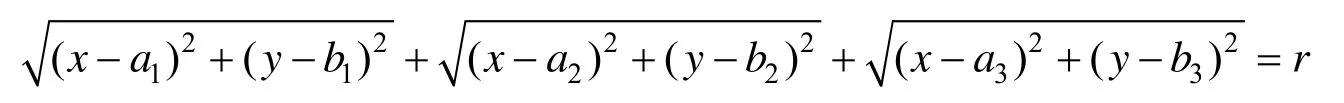
类似于椭圆，该公式表示到3个焦点的距离之和为定长的点的集合。其中r为20，3个权重均为1。通过改变焦点的坐标，改变正三角形边长 l，控制正三角形的大小变化，得到三焦点曲线的形状，如图1所示。

分析与结论：通过绘图实验可以发现，当焦点三边形为正三角形时，对应的三焦点曲线始终为中心对称图形。①当l/r比较小时，三焦点曲线类似于圆形。随着l/r的增大，曲线逐渐变为馒头和宝石形。②当l/r较大时，形成规则的中心对称曲线。③当边长为10时，3个焦点的坐标正好位于曲线的3个顶点处；当边长超过10时，曲线在焦点多边形的内部，并逐渐缩小；在 l≥13后，没有满足条件的曲线。

(2) 有且仅有一个负焦点时，限定定长和权重值，正三角形的边长不断增大，观察三焦点曲线形态的变化情况。三焦点曲线的公式为

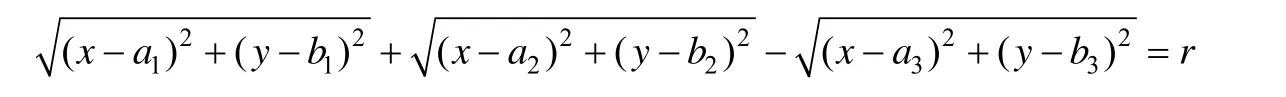
实际上，该公式表示到两个焦点的距离之和与到另一个焦点的距离之差点的集合，其中 r为20，通过改变焦点的坐标，改变三角形边长l，控制正三角形的大小不断变化，得到三焦点曲线的形状，如图2所示。

在图2的绘制实验中，3个焦点仍构成正三角形，通过固定定长r(本实验为20个单位)和权重(两个为1，一个为-1)，变化正三角形边长(边长l通过计算机模拟从2个单位逐渐增加至20 000个单位)的方式，以获得三焦点曲线形状。

图1 限定定长和权重值，正三角形的边不断增大，三焦点曲线形状变化

图2 限定定长和权重值，正三角形的边长不断增大，三焦点曲线形状变化情况

在正三角形边长较小时，l/r较小，曲线形状接近圆形，焦点三边形在图形的中心；随着正三角形边长增大，l/r增大，焦点三边形逐渐向负焦点对应一侧的曲线偏移。该焦点相应一侧的曲线逐渐平缓并在l=8时接近水平；随着l进一步增大，负焦点对应一侧的曲线逐渐内凹，曲线形成类似心形线的曲线，在 l= 10时，曲线通过上侧焦点； l＞ 10时上侧曲线进入焦点多边形；随着l进一步增大，曲线逐渐变为元宝形；当l/r非常大时，曲线逐渐变为橘子瓣形直到月牙形。整个实验过程形成的三焦点曲线都是关于通过上侧焦点的竖直直线的轴对称图形。图 2中最后一图给出了边长由2到10变化时曲线的详细对比图。

2.2 焦点多边形为等腰三角形

(1) 焦点多边形为等腰三角形，且无负焦点时，限制定长，改变等腰三角形的高。多焦点曲线公式为

三角形底边定点的坐标(0,0)、(2,0)，高度H从1逐渐变为 20，利用软件绘制曲线的变化情况，部分试验结果如图3所示。

图3 限制定长，改变等腰三角形的高度，三焦点曲线形状变化情况(H为等腰三角形的高，括号中的数字为第3个焦点的坐标)

从图3中可以看出，当高度较小，H/r较小时，焦点曲线接近圆形；随着高度增大，H/r变大，三角形逐渐变大、变高，焦点曲线被沿纵向拉长，并形成上小下大的类似鸡蛋的卵圆图形；当H/r再增大时，上方逐渐形成一个尖点，焦点曲线变为水滴状；当达到临界状态，上方焦点通过焦点曲线后，上方曲线逐渐穿过焦点多边形，并形成较小的卵圆图形；H/r进一步增大时，卵圆图形逐渐缩小，直至没有满足焦点曲线方程的曲线和点。

(2) 焦点多边形为等腰三角形，且有一个负焦点时，限制定长，改变等腰三角形的高度。多焦点曲线公式为

底边定点的坐标(0,0)、(2,0)，高度H从1逐渐变为 20，利用软件绘制曲线的变化情况，部分试验结果如图4所示。

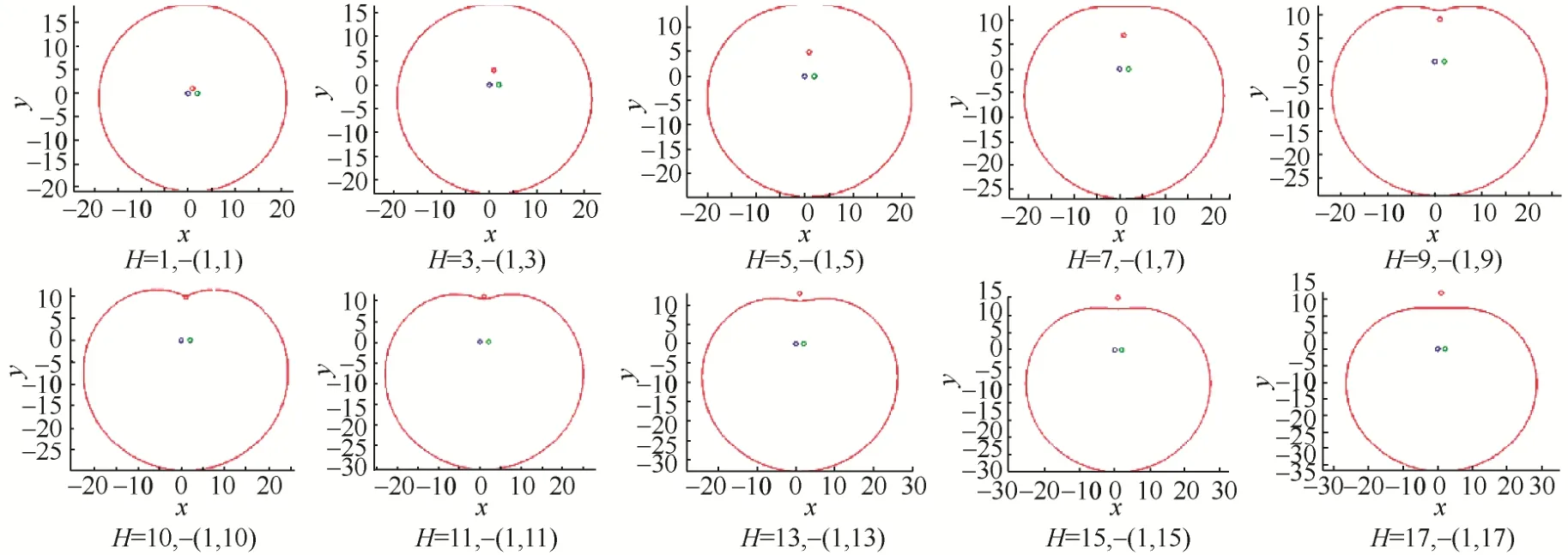
图4 限制定长，改变等腰三角形的高度，三焦点曲线形状变化情况(H为等腰三角形的高，括号中的数字为第3个焦点的坐标)

顶点处的焦点对应焦点曲线公式中权重为负的项，从图 4中可以看出，当高度较小，三角形相对形状较小，H/r较小，焦点曲线接近圆形；

随着高度增大， H/r变大，三角形逐渐变大，变高，顶点上方的曲线变得平缓并在达到水平之后内凹，此时曲线在三角形上方；当 H /r再增大时，上方曲线内凹形成类似心形线的曲线，曲线穿过上方顶点后，上方曲线进入焦点多边形，曲线再次变平缓。试验中曲线均为和等腰三角形同轴的轴对称图形。

2.3 3个焦点位于一条直线上

(1) 3个焦点排列在一条直线上，且无负焦点时，固定定长，变化焦点间的距离，三焦点曲线公式为

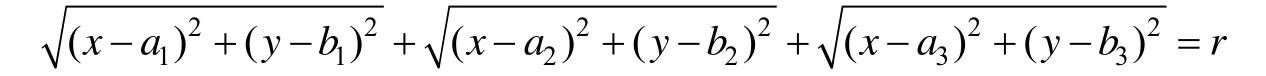
初始焦点值为(0,0)，(1,0)，(20,0)定长取30，将中间的焦点按照确定的规律从左向右移动，绘制曲线图形，如图5所示。

图5 3个焦点在一条直线上，变化焦点距离时三焦点曲线变化情况

当3个焦点在一条直线时，三焦点曲线为以该直线为对称轴的中心对称图形，左右两侧均为卵圆形状，当中间的焦点从左向右移动时，曲线的最高点和最低点从左侧移到右侧，和焦点数目较多的一侧一致，当中间的焦点移动到两侧焦点正中间时，曲线高低点也移动到正中间。

(2) 3个焦点排列在一条直线上，且具有一个负焦点时，固定定长，变化焦点间的距离，曲线公式为

3个焦点在一条直线上，其中第3个焦点对应负多项式。初始的焦点值为{(0,0), (1,0), (20,0)}，定长取30，将第2个焦点按照确定的规律，从左向右移动，绘制曲线图形，如图6所示。

两侧焦点对应公式的系数，分别取正号和负号，曲线在取负系数时对应焦点的一侧向内凹陷，且曲线大部分都在该方向的反向存在。将中间的焦点从左侧移动到右侧时，曲线向右侧移，且右侧的凹陷逐渐平缓并消失，最后形成卵圆图形。

图6 3个焦点在一条直线上，变化焦点距离时三焦点曲线变化情况

2.4 三焦点中两焦点重合

(1) 固定定长，移动重合焦点的位置时三焦点曲线的变化。三焦点曲线的公式为

多焦点曲线3个焦点中有2个焦点重合，固定定长，将重合的焦点逐渐远离定点焦点进行试验，设初始焦点为：(1,1)、(2,1)，其中(2,1)为重合焦点，初始定长为20，绘制的图形如图7所示。

当重合焦点从左向右按照一定规律移动时，曲线由圆形逐渐变为卵圆；进一步向右移动焦点，曲线逐渐变为底部对应重合焦点的水滴形曲线，之后变为不规则曲线，只有少许点满足曲线方程，当重合焦点移动到足够远时，没有满足要求的点。

(2) 2焦点重合，固定焦点位置改变定长时三焦点曲线的变化。曲线的公式为

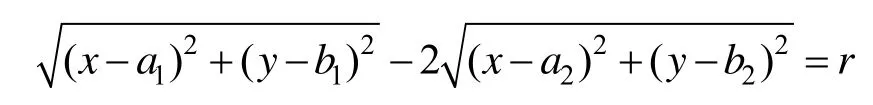
多焦点曲线3个焦点中有2个焦点重合，第1个焦点的权重为1，重合的焦点权重为-2，从1开始不断增加定长，绘制的三焦点曲线图形如图 8所示。

随着定长的增大，曲线逐渐变为不规整的卵圆，之后满足公式的点越来越少，最终没有满足条件的点。

通过大量绘制三焦点曲线，总结得到三焦点曲线主要性质及规律：

(1) 三焦点曲线形态主要受焦点的相对位置、定长和权重值的影响。

(2) 三焦点曲线的轴对称特性与焦点三边形的对称性一致。随着定长相对焦点三边形的逐渐增大，三焦点曲线会变得越来越规则，并逐渐接近圆形，因而对称性逐渐和圆形一致。

(3) 当焦点的权重均为正值时，三焦点曲线为一种光滑凸闭合图形，在少数极端情况下会出现退化，三焦点曲线出现一阶连续点，或者三焦点曲线直接退化为有限个点。当存在焦点的权重为负值时，三焦点曲线变化过程中会出现凹陷，且凹陷位置与权重为负的焦点位置相对应。

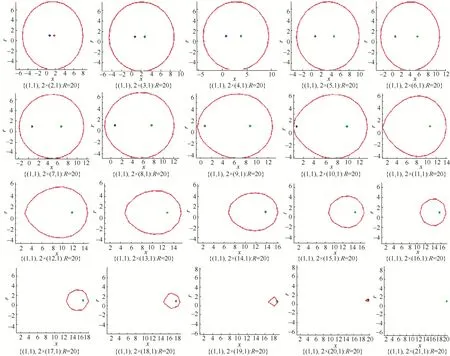
图7 2个焦点重合，变化重合焦点位置时三焦点曲线的变化情况

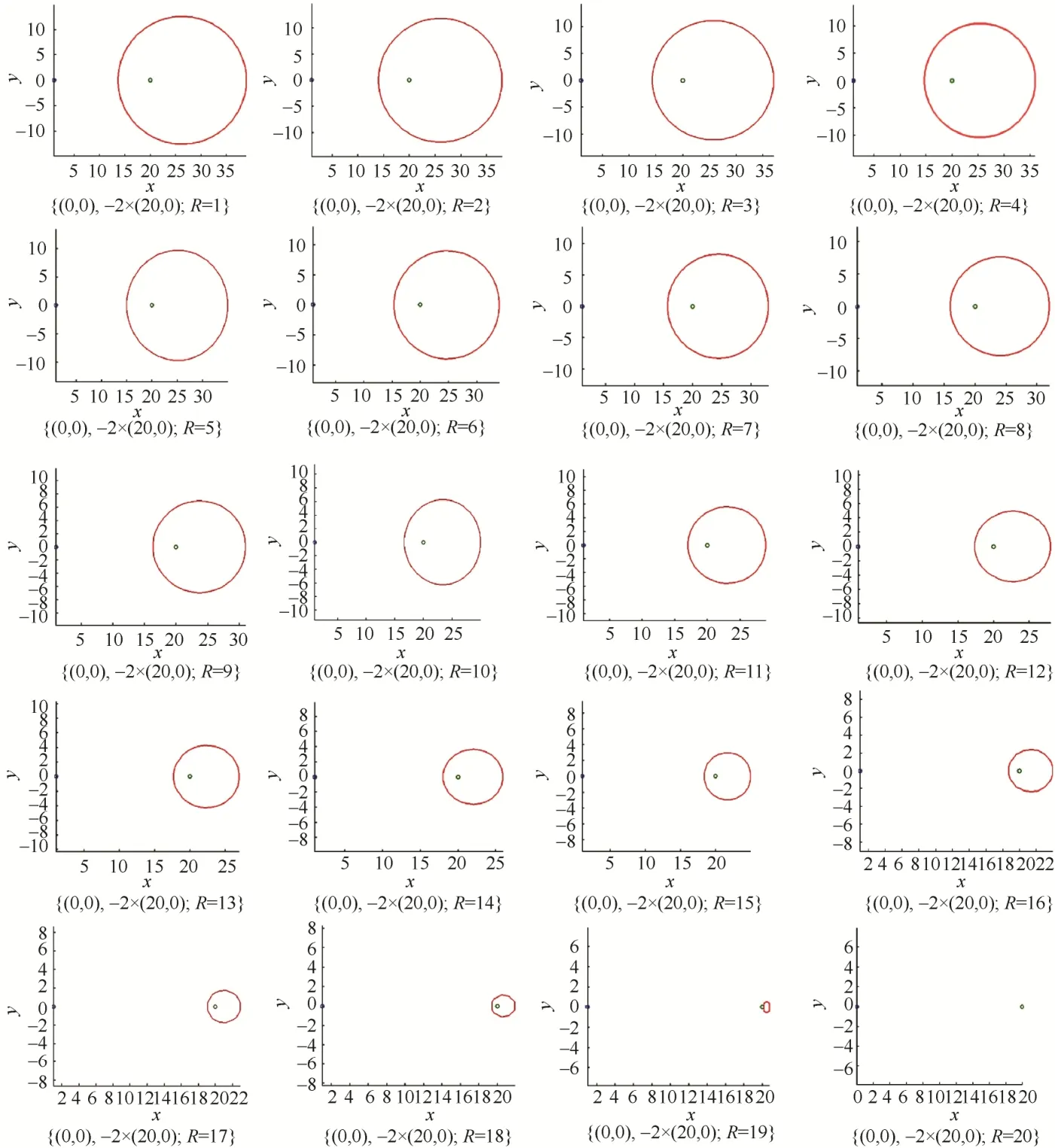
图8 重合焦点的权重为负值，改变定长时三焦点曲线的变化情况

3 物体图像轮廓对应的三焦点曲线

在CPU Core i5；内存8 GB，Windows 7环境下进行实验，采用Matlab 2010b软件进行编程，在实验的过程中，选取的图像绝大部分来自于实拍物体。

3.1 图像处理

利用Matlab 2010b软件对实物图像进行处理。首先读入目标图像，利用函数 im2bw将 RGB模式的原始图像转换为二值图像，使用最大类间差方法找到图片的一个合适阈值，进行二值化转化；构造结构化元素，并利用im rode函数对刚刚产生的二值图像进行腐蚀，腐蚀的结果是把二值图像 BW中比较小的孔洞进行腐蚀掉，使除了图形就是一个黑色的背景，不存在小洞，利用bwboundaries函数进行二值图形的边缘提取，并且去掉内部的图像，将提取后边缘各个点的坐标，以矩阵的形式进行保存，如图9所示。

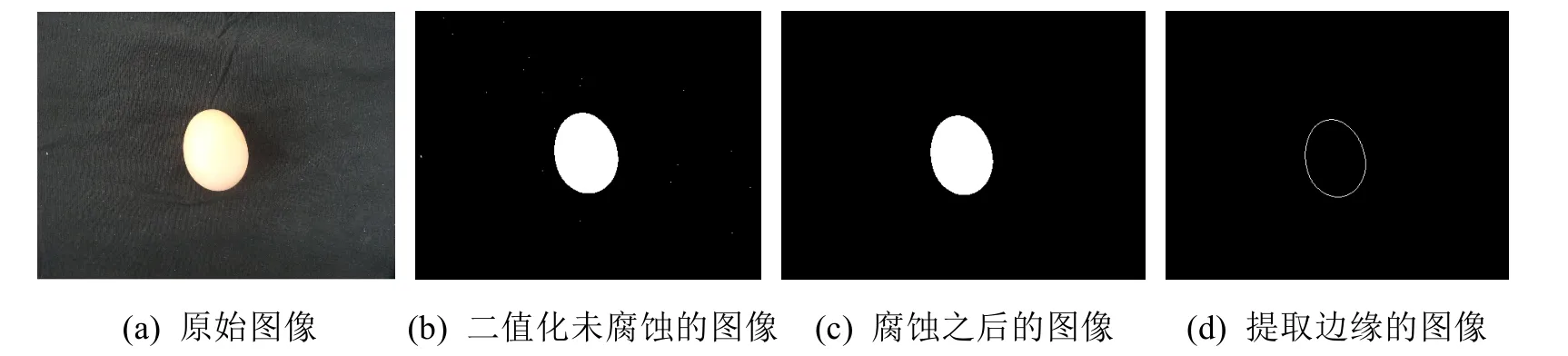
图9 图像处理

3.2 拟合三焦点曲线

虽然可以采用Hough变换的方法检测椭圆[9]，但Hough变换方法并不适合于检测本文的对象。本文设计了一种巧妙的拟合方法，首先通过图像处理的办法，提取实际物体图像的轮廓边缘坐标信息(xi, yi)，其次构造目标最优化函数fun_in函数，通过fm incon函数对fun_in进行最优化求解，求出fun_in中对目标数据(xi, yi)残差最小的参数，函数将利用包含梯度法等优化算法，进行曲线拟合和参数求解。利用上一节量化参数三焦点曲线形态分析，确定目标图像参数的大概范围。本实验对初值的选取没有很强的依赖性，fm incon初值在参数取值的较大范围内可随机取值。检查参数曲线中是否存在非零点，利用循环语句遍历曲线方程中的点的坐标，使用fzero()函数对参数曲线的零点坐标进行检查并标记，对于可能因为局部残差、噪点或其他原因引起的非零点，可以求取 xi极小邻域范围内的极小值点，并进行标记。最后输出曲线公式中对应的各个参数，画出曲线图，并给出误差分析图。误差分析图是在纵向坐标一致的情况下，比较曲线上点和原始图像上已知点之间的误差。

3.3 实验说明

选取了大量常见物体的照片进行测试，部分实验结果如图10所示。图10中从左至右的4幅图分别为原始输入图像、提取边缘坐标后的图像、拟合后的图像和误差分析图像。

在Matlab中图像按照矩阵的形式进行表示和存储，第1、2幅图像的像素点的坐标信息都是以矩阵的形式在计算机中进行存储。第 1幅图像为物体的原始的照片或者图片；第 2幅为提取边缘后的边缘图像；在第3幅拟合图像中，用y表示纵向的坐标，用x表示横向的坐标，分别对应行、列坐标信息。蓝色圈表示从原始图像上提取的点的坐标，表示为(x,y)，红色曲线为拟合后的图像，点的坐标表示为(x,ys)。在误差图像中，横坐标表示图像对应的点，纵坐标表示对于相同的 x对应的点，拟合后的曲线的坐标与原始图像边缘点的对应坐标之差，即y-ys。

3.4 实验结果分析

在图10的拟合图像中，蓝色的圆圈图像表示从图像边缘提取的坐标点，红色曲线为拟合后按照参数方程画出的曲线。从实验可以看出，对于鸡蛋、圆滑的石头等物体误差非常低，在1以内，曲线几乎完全重合；猕猴桃和柠檬的误差也比较小，在1.5左右，主要由于其表面不够光滑；桃子等的误差也很低。

为了方便统计误差率，用式(1)来计算图像的平均误差K，其等于对所有拟合曲线与原图像边缘曲线的 Y坐标之差求和再除以坐标总数；用式(2)来表示平均误差率，其等于所有拟合曲线与原图像边缘曲线的 Y坐标之差再全部求和，除以对应

原图边缘曲线坐标值之和，并用该结果除以坐标总数。式(1)和(2)为

图10 实验结果

利用拟合方法求出图像轮廓边缘曲线对应的三焦点曲线各个参数，结果如表1所示。

表1 实验结果的具体数据

4 总 结

通过实验分析发现，实验本身误差受初值的选取影响不大。三焦点曲线能够用来表示、分析、匹配和识别大量物体图像轮廓，如鸡蛋或者桃子、草莓、苹果、柠檬等水果，以及石头、水滴、手雷、萝卜等物体。用三焦点曲线拟合鸡蛋、桃子、柠檬、猕猴桃图像轮廓等误差率非常小，能够很好表示这类物体，因此三焦点曲线能够精确化表示这类物体。

[1] 管贤根, 管 杰. 多焦点圆及其椭圆和卵圆[J]. 图学学报, 2013, 34(2): 52-64.

[2] Barrowclough O J D. A basis for the implicit representation of planar rational cubic Bézier curves [J]. Computer Aided Geometric Design, 2014, 31(3/4): 148-167.

[3] Eyal K, Trevor H, Haim W. 3-D curve matching using splines [J]. Journal of Robotic Systems, 1991, 8(6): 723-743.

[4] Cohen F S, Huang Z, Yang Z. Invariant matching and identification of curves using B-splines curve representation [J]. IEEE Transactions on Image Processing, 1995, 4(1): 1-10.

[5] Sederberg T W, Chen F L. Implicitization using moving curves and surfaces [C]//Computer Graphics, 29(Annual Conference Series), Proceeding of Siggraph’ 1995. New York: ACM Press, 1995: 301-308.

[6] Sederberg T W, Anderson D C, Goldman R N. Implicitization, inversion, and intersection of planar rational cubic curves [J]. Computer Vision, Graphics, and Image Processing, 1985, 31(1): 89-102.

[7] Floater M S. Rational cubic implicitization [M]. In: Daehlen M, Lyche T, Schumaker L. (Eds.), Mathematical Methods for Curves and Surfaces. Nashville, TN, US: Vanderbilt University Press, 1995: 1-9.

[8] Busé L, Ba T L. Matrix-based implicit representations of rational algebraic curves and applications [J]. Computer Aided Geometric Design, 2010, 27(9): 681-699.

[9] Tsujiy S, Matsumoto F. Detection of ellipses by a modified Hough transform [J]. IEEE Transactions on Computer, 1978, 27(9): 777-781.

A K ind of Trifocal Points Curve

Gao Mantun, Li Yang, Wang Shuxia, Wang Shouxia

(School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an Shaanxi 710072, China)

A kind of trifocal points curve is mainly researched. Firstly, the concept and formula of this kind of trifocal points curve is presented, and the properties of the trifocal points curve are also analyzed. Secondly, quantitative and shape analysis is made on the trifocal points curve by turning its parameters, and the programm ing method is used to realize the shape analysis of the trifocal points curve. The properties and rules of the trifocal points curve are analyzed and summarized. Finally, the parameters of the trifocal points curve are calculated by using of the image processing and fitting method which is the contours of images of some objects. Moreover, the error analysis is given and the fitting curve is described. The experiment results show that the trifocal points curve can be the precise representation of the contours of the images of some natural objects.

trifocal points curve; natural object; image processing; curve fitting; error analysis

TP 391.41

10.11996/JG.j.2095-302X.2016040457

A

2095-302X(2016)04-0457-10

2016-02-29；定稿日期：2016-04-20

国家自然科学基金青年基金项目(51105310)；陕西省自然科学基础研究计划项目(2016JM 6054)；浙江大学CAD&CG国家重点实验室开放课题项目(A1615)；西北工业大学研究生创意创新种子基金项目(Z2016082)

高满屯(1962−)，男，山西襄汾人，教授，硕士。主要研究方向为理论图学、视觉与图像。E-mail：gaomant@nwpu.edu.cn