基于几何配准的三维模型几何比对方法研究

周 培， 刘 铭， 王 腾， 杨 欣， 聂蓉梅

(1. 北京宇航系统工程研究所，北京 100076；2. 山东山大华天软件有限公司，山东 济南 250000)

基于几何配准的三维模型几何比对方法研究

周 培1， 刘 铭2， 王 腾1， 杨 欣2， 聂蓉梅1

(1. 北京宇航系统工程研究所，北京 100076；2. 山东山大华天软件有限公司，山东 济南 250000)

针对设计师在进行协同建模时无法快速查看模型变更信息的问题，提出了快速比对两个模型几何差异的方法。首先，通过等步长采点获取两个模型的点云数据；然后，利用主元分析法计算两个点云的特征向量从而获取点云的参考坐标系，推导两个点云参考坐标系的坐标变换，将两个点云调整到一致，即可实现点云的初始配准；最后，利用最近点迭代法对两个点云进行精确配准，记录配准后两个点云中的非重叠区域，可获取两个点云的几何差异区域。测试结果表明该方法可以有效识别两个模型的几何差异。

点云；几何配准；几何比较；协同建模

随着三维CAD技术的迅速发展，三维CAD软件已经在制造业、工程设计等领域广泛应用。相对二维工程图设计，设计者们在利用CAD软件设计产品时也经常面临新的问题。由于产品方案随时可能发生变更，设计师经常会根据上级发出的变更通知对已有的模型进行更改，并手工记录更改点。然而在模型较复杂、变更细节较多时，如果仍然采用手工记录的方式，一方面难以避免漏记、错记，另一方面极不易察觉关联尺寸等非直接变更导致的更改。由此产生的变更信息用于

指导后续的生产制造，势必会影响产品质量。因此设计师在设计产品时，尤其是多位设计者进行协同建模时，非常需要有工具可以提供三维模型的几何比较，让每位设计者可以在本地不同版本的模型中快速定位更改点。

目前国内还没有一款专门提供模型几何比较功能的工具，但有关模型比较的研究有很多，多数基于配准算法的模型相似性研究，主要应用于质量检测、模型检索、人脸识别等技术领域[1-5]。如张志波等[1]提出改进的工业CT图像与CAD模型的比对检测方法，主要研究了CT图像与CAD模型的几何误差，及数字化测量设备对产品质量的检测。美国PTC公司研发的三维CAD软件Creo Parametric已经在国内航天、工程机械领域广泛使用，其提供了零件级模型的几何比较功能，但此功能需进行原点配准，不适于两个模型没有配准对齐的场景。模型的配准对齐是进行模型比对的关键，目前常用的配准算法如Besl和M cKay[6]提出的基于优化理论的最近点迭代法(iterative closest point, ICP)，以及近期的基于曲率或基于几何特征的点云比对算法[7-8]，还未被应用于三维模型几何比对领域。

针对上述现状，本文提出了一种基于几何配准的几何比较方法。测试结果表明，该方法可以较好地对齐两个三维CAD模型，有效找出两个模型的几何差异，并具有较好的鲁棒性，成功集成应用于Creo Parametric三维设计平台，改进现有几何比较方法。

1 Creo Parametric的几何比较方法及不足

1.1 Creo Parametric的几何比较方法

作为第一款运用“参数化设计”思想的三维CAD软件，Creo Parametric自身提供了零件级的几何比较。可以在“零件”模式下，比较两个零件或一个零件的两个不同版本，获得两个零件或不同版本间存在几何差异的图形报告。

Creo Parametric自身几何比较的原理：生成第一个零件的点云数据，然后将其叠加到第二个零件上。之后，Creo Parametric生成两个零件间偏差的着色显示，并在图形窗口中显示出来。

执行Creo Parametric几何比较功能时，需要设置“测量间距”和“公差”，其中“测量间距”用于控制点云密度，“公差”用于控制显示。

使用该工具的前提是两个零件已配准对齐，如果两个零件的几何拓扑信息一样，但位置不同，那么Creo Parametric自身的几何比较将会认为两个零件存在几何差异。

1.2 Creo Parametric几何比较方法的不足

下面演示Creo Parametric的几何比较效果：首先利用 Creo Parametric创建一个简单100×100×100的正方体，作为原始模型，如图1(a)所示。然后，将原始模型沿x轴正方向移动30 mm，沿y轴正方向移动10 mm，得到新的模型，作为更改后的模型，如图1(b)所示。

图1 两个正方体模型：几何相同，位置不同

执行Creo Parametric的几何比较功能，比较图 1中的两个正方体模型的几何差异，比较效果如图2所示。

Creo Parametric在比较两个几何完全相同但位置不同的三维CAD模型时，会判定两个模型存在几何差异。因此，现有Creo Parametric的几何比较方法并不适用于比较两个姿态未对齐的三维模型，存在较大局限性。

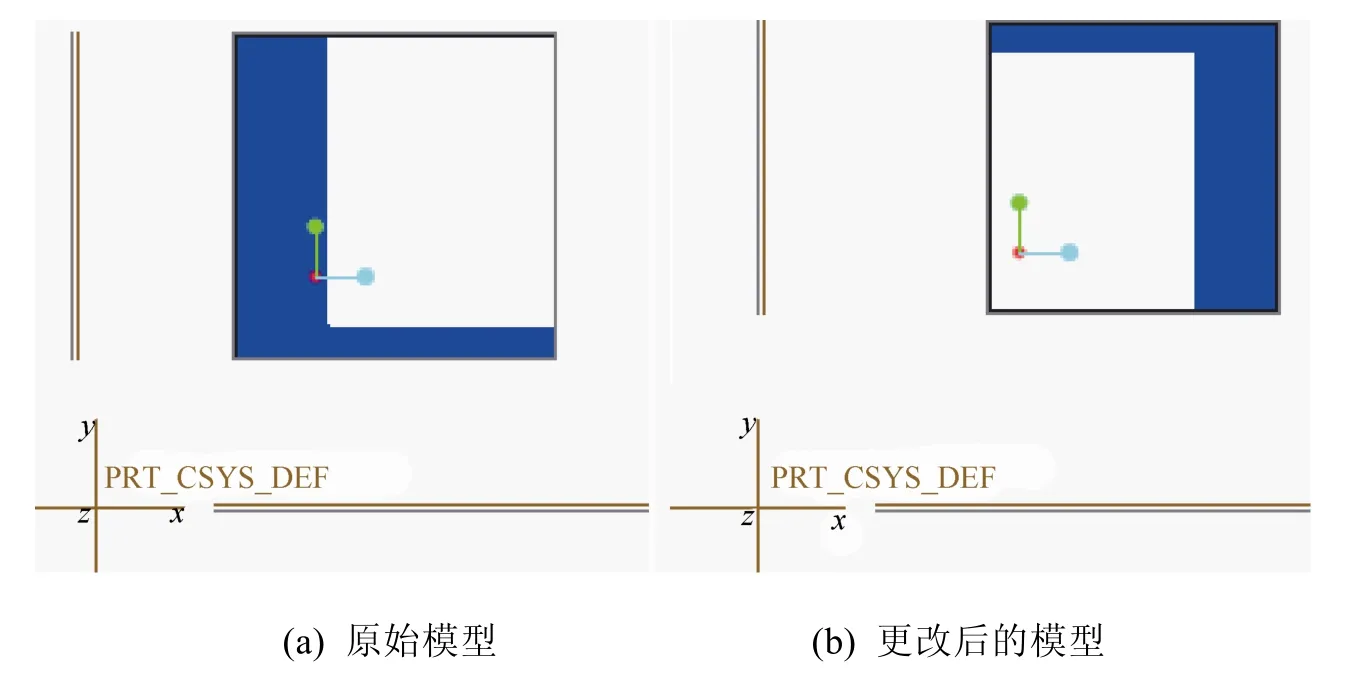
图2 Creo Parametric几何比较效果：蓝色区域即几何差异区域

2 基于几何配准的几何比较方法

针对Creo Parametric几何比较方法的不足，本文提出了一种基于几何配准的几何比较方法。该方法的基本原理是通过几何配准来匹配两个模型点云的重叠部分，记录不重叠区域中的点作为差异点，将差异点所在几何面作为差异显示。算法流程如图3所示。

图3 基于几何配准的几何比较方法的算法流程图

2.1 读取两个模型的几何信息

通过两种方法可获取两个三维模型的几何拓扑信息：①直接通过模型所属CAD软件的二次开发接口获取；②在模型所属CAD软件未提供二次开发接口的情况下，将模型文件转换成step格式，再按step标准读取模型step文件中的几何信息。

2.2 获取模型的点云

等步长对模型所有面进行采点，获取的点集作为模型点云数据。所述“步长”就是采点间距。

2.3 进行初始配准

获取到点云数据后，构造协方差矩阵来计算两个点云的局部坐标系，并通过其对两个模型点云进行初始配准。利用点云数据构造协方差矩阵的方法，在统计学中被称为主元分析法（principal Component analysis, PCA）。PCA的目的是“降噪”、“去冗余”，构造对角化协方差矩阵。

上述构造协方差矩阵的方法如下：

设有集合 S= {X1,X2,···,Xm}，S中的每个元素都是一个样本集，那么由这些样本集构成协方差矩阵

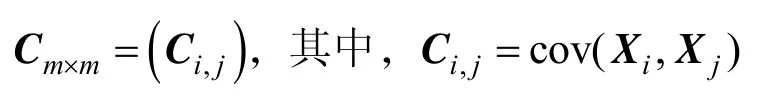
举一个三维的例子：假设数据集有 3个维度{X,Y,Z}，每个维度样本集含有n个元素，则协方差矩阵为

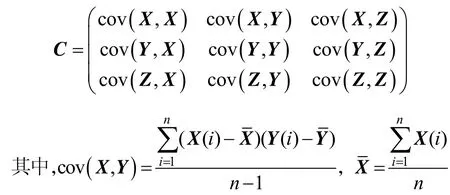
综上所述，协方差矩阵的意义是为了描述维度之间的线性相关关系。获取到点云数据后，通过点云中的样本点坐标，构造{X,Y,Z} 3个维度的

协方差矩阵。然后，通过对角化协方差矩阵使得维度间的相关性尽可能小，并使得保留下来的维度的方差尽可能大。对角化后的矩阵，其对角线上是协方差矩阵的特征值，取最大的 3个特征值对应的特征向量即可作为点云的3个主轴方向。

下面简述两个模型点云初始配准[9]的实现流程：

步骤1. 利用点云数据构造协方差矩阵。

步骤2. 利用Jacobi方法计算协方差矩阵的特征值和特征向量，取最大的 3个特征值对应的特征向量作为点云局部坐标系的3个主轴方向。

步骤 3. 计算点云重心，作为点云局部坐标系原点。

步骤 4. 将两个点云的参考坐标系调整到一致，即可达到两个点云的初始配准，最终使得两个模型的姿态自动对齐。

2.4 进行精确配准

完成初始配准后，两个模型点云大致重合，为了尽可能缩小点云之间的旋转和平移错位，还需要利用ICP算法[9]对两个模型点云进行精确配准。

ICP算法是应用最为广泛的几何配准算法，其是基于最小二乘法的最优匹配算法，目的在于寻找最小二乘逼近的坐标变换矩阵。ICP算法中最经典的方法是“Point To Point”就近点搜索算法，这个方法主要运用kd-tree的方法实现就近点搜索。其中，kd-tree是一个二叉树的数据结构，每个节点表示一个空间范围，主要用于快速检索在 kd-tree中与查询点距离最近的数据点。下面简述两个模型点云精确配准的实现步骤。

设

其中，P、Q表示两个模型的点云数据，pi表示为点云P中第i个数据点，qj表示为点云Q中第j个数据点，M为点云P的数据点个数，N为点云Q的数据点个数，R3表示为实数点集。

运用点到点的 ICP进行精确配准[6,9-10]的主要步骤：

步骤 1. 利用 kd-tree的数据结构存储点集 Q的所有数据点。

步骤2. 遍历点集P中的所有点pi，在点集Q检索最近点 qt。令 xi=qt，生成新的点集 X, X = { x| x ∈ R3, i = 1,2,···,M}。由于每个点p∈P都

i ii能在点集Q中找到一个对应的最近点，所以点集P与点集 X的数据点个数相同，且对应的点具有相同的下标，即pi的最近点为xi。

步骤3. 计算点集P的重心坐标，记为μp；计算点集X的重心坐标，记为μx。

步骤4. 利用单位四元数法计算点集P到点集X的最佳旋转变换 R，单位四元数法的算法流程如下：

不妨先设旋转向量为单位四元数q=［q , q, q, q］T， 其 中 q≥0， 且

R0 1 2 30。

首先，构造点集P、X的协方差矩阵

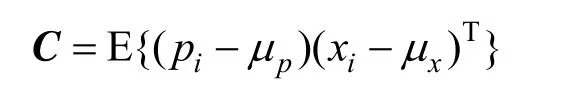
然后，根据矩阵C构造4乘4正定矩阵

其中，tr(C)表示矩阵C的对角线元素之和，I3表示3阶单位矩阵，。

最后，计算矩阵N的特征值和特征向量，其最大特征值对应的特征向量即最佳旋转向量 qR，从而，得最佳旋转矩阵R，即

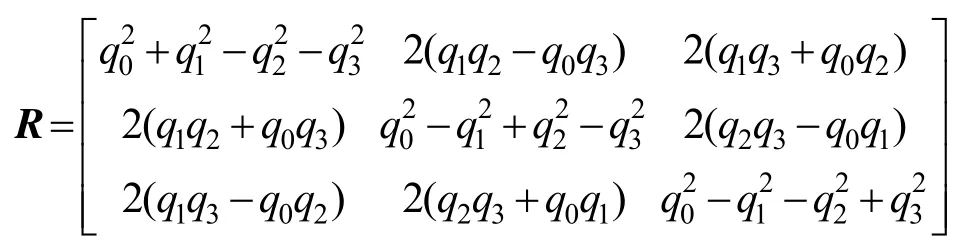
步骤5. 计算最佳平移向量 T =μx- Rμp。

步骤6. 利用得到的旋转变换R和平移变换T对点集 P进行变换，得到经过坐标转换后的点集Trans(P)。

步骤7. 计算点集Trans(P)到点集Q的距离平方和dk，其中，dk表示第k次迭代计算的距离平方和。若大于或等于预先给定的阈值τ(τ＞0)，则返回步骤2；直到或迭代次数达到预设的最大值时，迭代终止。

2.5 记录几何差异

精确配准后的两模型点云会重叠在一起，记录不重叠的点作为差异点。应用 OpenGL的显示库，先将两个原始模型显示出来，然后涂色显示差异点所在的几何面。显示效果以几何面为单位。

3 Creo Parametric几何比较方法的改进

虽然第 2节给出的算法可以解决两个模型姿态未对齐的应用场景，但也存在一个问题：由于最终获取的差异点云中可能是受设计师直接更改影响的点云，所以可能无法真正反映模型的实际变更。

以图4的两个零件为例，图4(a)是原始模型，图4(b)是更改后的模型，图中红色线框部分即设计师的实际变更。

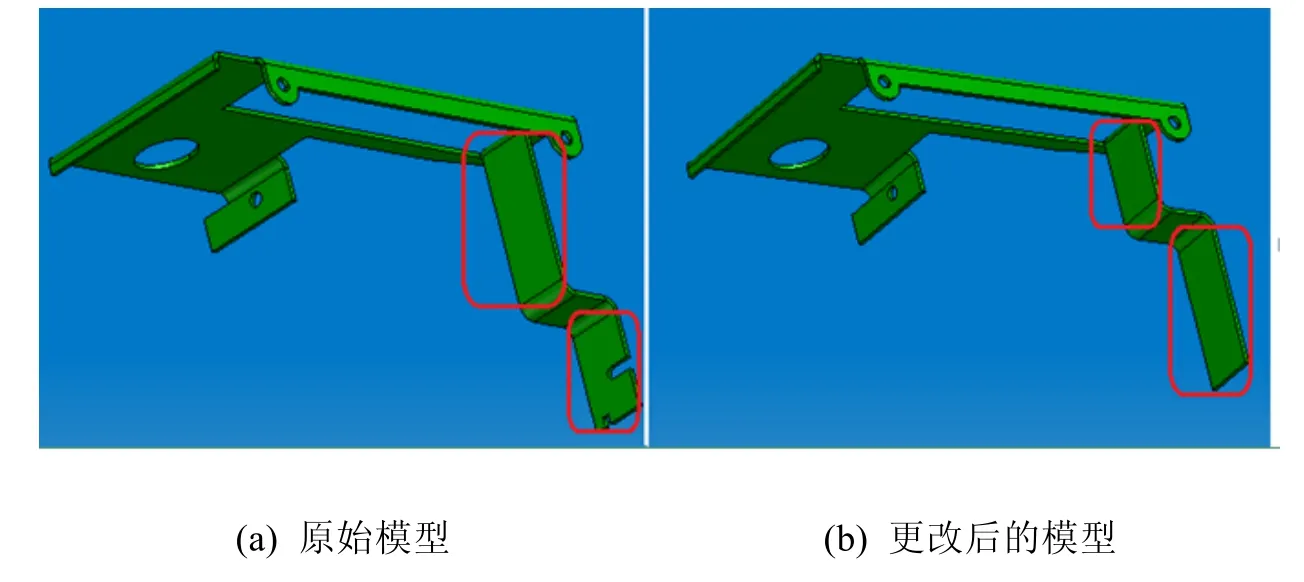
图4 两个存在几何差异的模型：线框区域是实际几何变更

利用第2节的算法进行比较，会判定图5中红色线框区域为两个模型的差异，达不到“显示设计师实际变更”的比对效果。

图5 基于几何配准的几何比较方法的比对效果

为了解决上述问题，本文提出了一种改进的Creo Parametric几何比较方法，该方法基于 Creo Parametric的建模机制：在建模时，生成的每个几何面都会有唯一对应的 ID，且若该几何面发生改变时，面ID不变。

根据上述机制，通过获取模型所有几何面进行面ID匹配，比较匹配上的几何面。算法步骤如图6所示。

图6 改进的Creo Parametric几何比较方法的算法流程图

步骤 1. 利用二次开发接口获取模型所有面ID，匹配两个模型中面ID相同的几何面。

步骤2. 获取匹配成功的两个几何面的几何信息。并通过等步长的面上采点法获取几何面的点云数据。

步骤3. 对两个面的点云数据进行配准，判断是否存在点间距在阈值之外的差异点。若两个面存在差异点，则记录两个面作为几何差异。

由于第2节已经介绍了点云配准的算法步骤，所以上述算法的第 3步中不再赘述。与上节不同之处在于，本节点云配准的采点对象是模型中通过面ID匹配的几何面，而上节则是直接对整个模型所有面进行采点。

改进的Creo Parametric几何比较方法利用面ID找出两个模型所有几何面的匹配关系，所以可真实反映设计师的实际变更。然而在应用上需满足一个前提条件：设计者在变更模型时，是在原有模型基础上进行几何修改，没有再重新创建原模型。如果设计师进行模型变更时，重新创建原有模型，那么所有几何面将生成新的面 ID，会导致更改前后的两个模型中不再存在面 ID对应关系，因此无法利用改进的Creo Parametric几何比较方法进行几何面匹配。

4 实例验证

本实验利用Creo Parametric设计了两组模型，如图 7所示。这两组模型都存在几何差异，且姿态未对齐。图 7中红色线框区域即两个模型的几何变更。

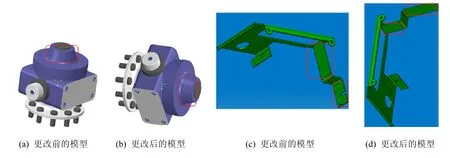
图7 两组原始模型

分别使用基于几何配准的几何比较方法、改进的Creo Parametric几何比对方法对两组模型进行几何比较测试。

4.1 基于几何配准的几何比较方法的测试结果

先获取两组模型的点云数据，点云数据如图8所示。

对两组模型点云进行初始配准，初始配准效果如图9所示。

对两组模型点云进行精确配准，精确配准效果如图10所示。

显示存在差异的点云区域，显示效果如图 11所示。

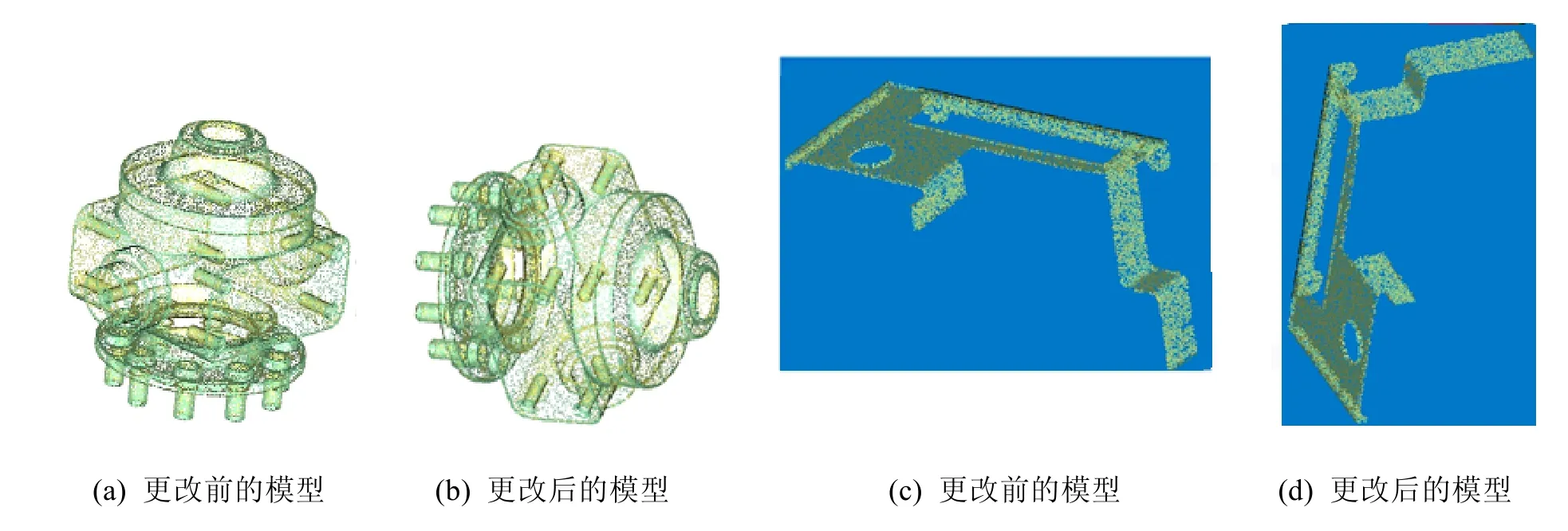
图8 两组模型的整体点云图

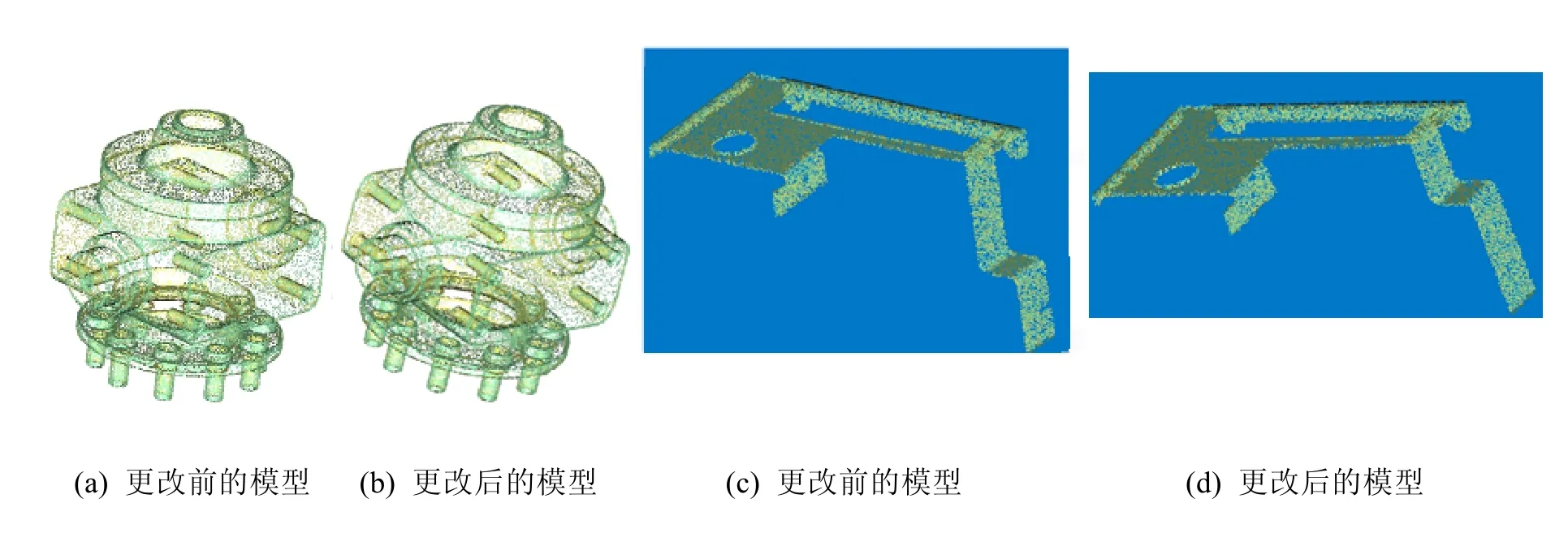
图9 两组模型点云的初始配准效果图

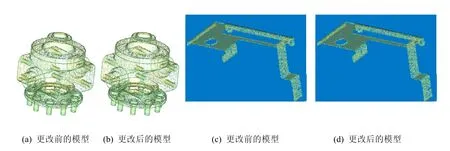
图10 两组模型点云的精确配准效果图

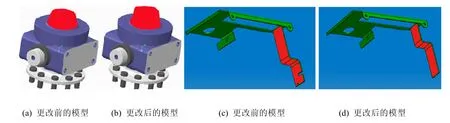
图11 基于几何配准的几何比对方法的比较效果图

从图11的比较结果来看，基于几何配准的几何比较方法可找出两个模型中所有存在差异的点云，且可较好地应用于模型姿态未对齐的场景。同时，由于该方法仅需要两个模型的点云数据，所以可适用于目前如 Pro/E、UG、CATIA、Solidworks等主流CAD软件。

4.2 改进的Creo Parametric几何比较方法的测试结果

改进的Creo Parametric几何比较方法，首先利用二次开发接口获取模型的几何面信息和对应的面ID，根据面ID匹配更改前后的两个模型的几何面。对匹配成功的几何面进行面上采点，获取面的点云数据，再利用“基于几何配准的几何比较方法”对两个面的点云数据进行对比。若两个面的点云存在阈值外的差异点，则为差异点云。两组模型的差异点云如图 12所示(差异点云以面为单位显示)。最后以几何面为单位显示模型差异，如图13所示。

图12 两组模型点云的差异面点云图

图13 改进的Creo Parametric几何比较方法的比较效果图

从图 13的比较结果来看，改进的 Creo Parametric几何比较方法明显具有更好的比较效果，可真实显示设计师的实际更改。但由于该方法需要两个模型存在面ID对应关系，所以应用范围较窄。

5 结 束 语

三维模型几何比对对实际的协同建模具有重要意义，本文给出的基于几何配准的几何比较方法，主要是将几何配准算法应用于模型姿态对齐，使得该方法可以处理更多的应用场景。但该方法并不存在对配准算法的修改和优化。针对“如何真实反映设计师的实际变更”的问题，本文也描述了一种改进的Creo Parametric几何比较方法。由实例验证可以看出，本文提出的思路是可行有效的，在计算机辅助设计中将具有良好的应用前景。

[1] 张志波, 曾 理, 何洪举. 改进的工业 CT图像与CAD 模型的比对检测[J]. 计算机应用研究, 2012, 29(6): 2242-2245.

[2] 史宝全, 梁 晋, 刘 青, 等. 基于约束搜索球的点云数据与 CAD模型精确比对检测[J]. 计算机集成制造系统, 2010, 16(5): 929-934.

[3] 王 勇, 唐 靖, 饶勤菲, 等. 一种新的散乱点云快速去噪算法[J]. 计算机应用与软件, 2015, 32(7): 74-78.

[4] 陶海跻, 达飞鹏. 一种基于法向量的点云自动配准方法[J]. 中国激光, 2013, 40(8): 179-184.

[5] 潘仁林, 达飞鹏, 邹红艳, 等. 基于面部曲线弹性匹配的三维人脸识别方法[J]. 图学学报, 2014, 35(3): 358-367.

[6] Besl P J, M cKay N D. A method for registration of 3D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[7] 马忠玲, 周明全, 耿国华, 等. 一种基于曲率的点云自动配准算法[J]. 计算机应用研究, 2015, 32(6): 1878-1880.

[8] 张 步, 姚顽强, 陈 鹏. 基于几何特征的建筑物点云配准方法[J]. 大地测量与地球动力学, 2015, 35(3): 416-419.

[9] 戴静兰, 陈志杨, 叶修梓. ICP算法在点云配准中的应用[J]. 中国图象图形学报, 2007, 12(3): 517-521.

[10] 朱延娟, 周来水, 张丽艳. 散乱点云数据配准算法[J].计算机辅助设计与图形学学报, 2006, 18(4): 475-481.

Research on Geometric Com parison of 3D M odels Based on Geometric Registration

Zhou Pei1, Liu M ing2, Wang Teng1, Yang Xin2, Nie Rongmei1

(1. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China; 2. Shandong Hoteamsoft Software Co., Ltd, Jinan Shandong 250000, China)

In order to help designers to check model changes quickly in a collaborative design, this paper focuses on how to rapidly compare geometric differences between two 3D models. First, the equidistant point clouds of two models are computed, and then a reference coordinate system of each point cloud is obtained by using the principal component analysis method. A transformation is then found to match the two point clouds to achieve an initial registration. Finally, the ICP (iterative closest point) method is used to realize accurate registration for the two point clouds. By computing the non-overlapping domain after the exact registration, we obtain the geometric differences between the two point clouds. The numerical example shows that the proposed method can effectively recognize the geometric differences of two 3D models.

point cloud; geometric registration; geometric comparison; collaborative modeling

TP 391

10.11996/JG.j.2095-302X.2016040483

A

2095-302X(2016)04-0483-08

2015-11-17；定稿日期：2016-01-17

国防基础科研计划重大项目(A0320131002)

周 培(1984–)，男，安徽全椒人，高级工程师，博士。主要研究方向为计算机辅助几何设计、数字化设计与仿真技术。

E-mail：zhoup2@126.com