Wang-Bézier型广义Ball曲线的降阶
王 燕, 李志明
(1. 合肥师范学院数学与统计学院,安徽 合肥 230601;2. 合肥工业大学计算机与信息学院,安徽 合肥 230009)
Wang-Bézier型广义Ball曲线的降阶
王 燕1, 李志明2
(1. 合肥师范学院数学与统计学院,安徽 合肥 230601;2. 合肥工业大学计算机与信息学院,安徽 合肥 230009)
分别应用扰动法和最佳一致逼近法,提出WBGB曲线的降阶算法,并给出了误差估计。实验结果表明,用最佳一致逼近法效果比扰动法要好。若利用扰动法得到的降阶曲线不能达到预期的误差,则可以先利用细分算法对曲线做细分,再逐段用扰动法降阶。WBGB曲线的降阶算法丰富了广义Ball曲线曲面的理论。
WBGB曲线;扰动法;最佳一致逼近
Ball[1-3]在 CONSURF系统中首次提出了 Ball基函数,Ball曲线的基函数仅限于三次,因此一些学者对其做了次数上的推广和研究,得到了高次的 Ball曲线,包括 Said-Ball曲线[4]与 Wang-Ball曲线[5]以及其一些扩展曲线[6-9]。这些扩展曲线与Bézier曲线有许多类似的性质,如计算稳定性、对称性、凸包性、端点插值性等,在曲线求值及升降阶的计算速度方面,Ball曲线明显优于 Bézier曲线。2000年,Wu[10]根据 Wang-Ball曲线和Said-Ball曲线的特点,又提出了两族新的带位置参数的广义Ball曲线(Wang-Said型广义Ball曲线和Said-Bézier型广义Ball曲线,简称WSGB曲线和SBGB曲线)。WSGB曲线包含了Wang-Ball曲线、Said-Ball曲线以及介于两者之间的曲线;SBGB曲线包含了 Said-Ball曲线、Bézier曲线以及介于两者之间的曲线,很自然的会想到能不能构造一组新的曲线,使其包含 Wang-Ball曲线、Bézier曲线以及介于两者之间的曲线。2008年,汪志华和朱晓临[11]通过引入位置参数,定义了能实现这一目标的曲线,称其为Wang-Bézier型广义Ball曲线,简称WBGB曲线。
对高次曲线曲面的降阶处理是实现不同阶数
的曲线曲面的数据转换的必要步骤。Hu等[12]曾讨论了Said-Ball曲线与Wang-Ball曲线的降阶,Wu[10]给出了WSGB曲线和SBGB曲线的降阶公式,江平和檀结庆[13]给出了WSGB曲线的降阶算法,刘刚和王国瑾[14]给出了SBGB曲线的显式降多阶逼近算法,但是关于WBGB曲线的降阶问题鲜有文章涉及。
本文分别应用扰动法和最佳一致逼近法,给出WBGB曲线的降阶算法及误差估计。实验结果表明,用最佳一致逼近法比扰动法的效果要好,若利用扰动法得到的降阶曲线不能达到预期的误差,则可以先利用细分算法对曲线做细分,再逐段用扰动法降阶。WBGB曲线的降阶算法丰富了广义Ball曲线曲面的理论体系。
1 Wang-Bézier型广义Ball曲线
定义1. 给定自然数m,L=0,1,…,m,n=2m+1,或n=2m,n+1个R2( R3)中的控制顶点{pi}, i=0,1,… ,n, n次WBGB曲线定义如下

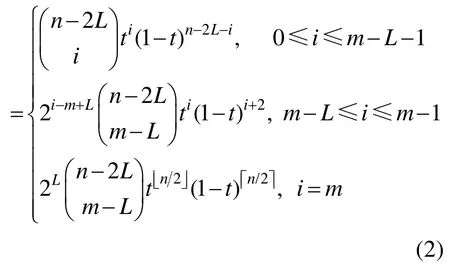
式中,「n」与「n」分别表示小于或等于n的最大的整数与大于或等于n的最小的整数。显然,当 L=0时,p( t, n,0)为Bézier曲线;当L=m时,p ( t, n,m) 为Wang-Ball曲线;当1 ≤L≤m-1时,为介于两者之间的曲线(如图1为L取不同值时对应的7次WBGB曲线)。
2 WBGB曲线的降阶
下面将给出将n次的 WBGB曲线式(1)降成n-1次曲线的方法,如式(3)


图1 7次WBGB曲线
2.1 WBGB曲线的可精确降阶条件
由定义1可知,在1≤L≤m的情况下,当n为奇数时,ωi( t, n, L)仅中间两项次数为n,即
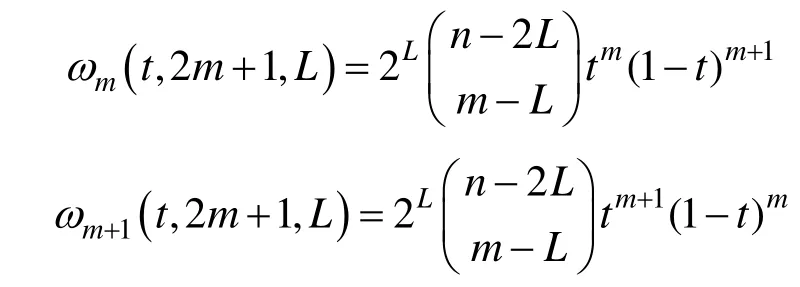
当n为偶数时,ωi( t, n, L)仅中间三项次数为n,即

故p( t, n, L)的首项系数为

定理1. 定义1中的n次WBGB曲线 (,,) p t n L可精确降阶为 n-1次WBGB曲线的充要条件,为其控制顶点满足:当 n=2 m+1时,Δpm=0;当n=2m时,,即
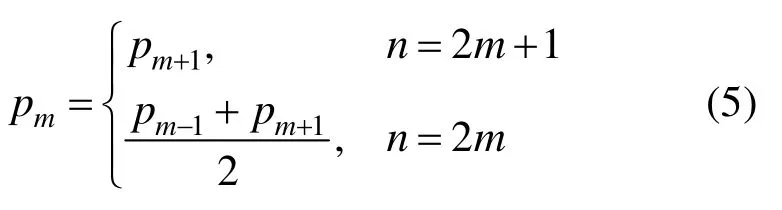
根据n次WBGB曲线可精确降阶的条件,以及文献[7]中给出的升阶公式,就可以得到 n-1次的WBGB曲线的控制顶点与n次WBGB曲线的控制顶点的关系。
定理2. 若定义1中的n次WBGB曲线可精确降阶为 n-1次,即满足式(5),设其n-1次 WBGB曲线所对应的控制顶点为,即
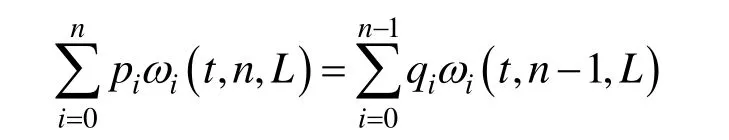
(1) 当n=2m+1,

(2) 当n=2m,
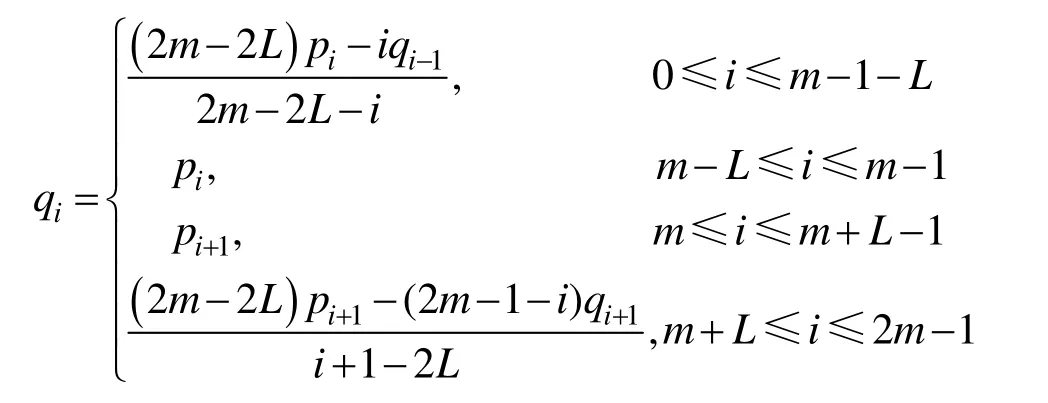
2.2 扰动法
对式(1)中的控制顶点添加适当的扰动εi, i=0,1,…,n,若添加扰动后的控制顶点,i=0,1,…, n满足式(5),即可精确降阶为形如式(3)中的n-1次多项式 q( t, n-1,L),则该多项式可作为式(1)的降一阶逼近,由定理 2可得如下的关系式:
(1) 当 n= 2 m+1,

(2) 当 n= 2m,

讨论n次WBGB曲线的降阶问题即为讨论如何取得适当的扰动 εi,使得扰动后的n-1次WBGB曲线与原曲线的误差最小,也即转化为求解优化问题1

由Lagrange乘数法可得:
(1) 当 n=2 m+1时,

代入式(6)得

(2) 当 n= 2m时,
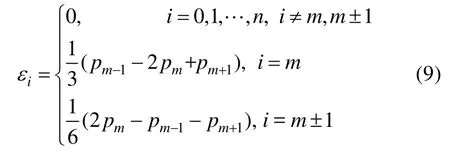
代入式(7)得
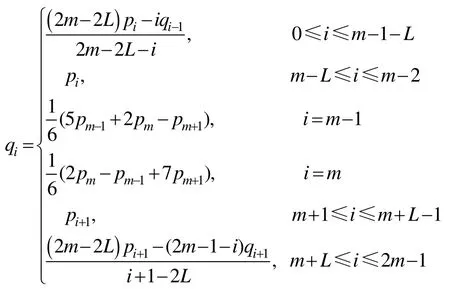
扰动法直观简易,从上述结论可以看出,其仅对中间几个控制点作修正,即可达到降阶逼近的目的,且当 n≥ 3时,扰动法的降阶多项式是保端点的。
2.3 最佳一致逼近法
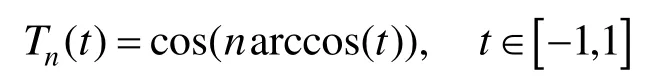
一般将其称为 Chebyshev 多项式或Chebyshev基函数。
引理1[15]. 若定义在区间[0,1]上的n次多项式p( t)都可表示为
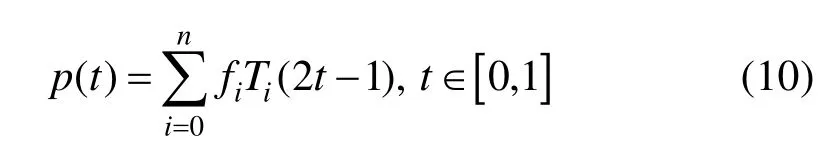
则n-1次多项式

为p(t)的最佳一致逼近。
引理2[15]. n次Bernstein基函数与Chebyshev基函数之间的转化关系为

文献[11]给出了n次 WBGB基函数的Bernstein基表示,文献[16]中给出了WBGB基函数的对偶泛函,并由此推导出Bernstein基函数到WBGB基函数的转化公式。
引理3[16]. n次Bernstein基函数可由WBGB基函数表示为:
(1) 当n=2 m+1时,
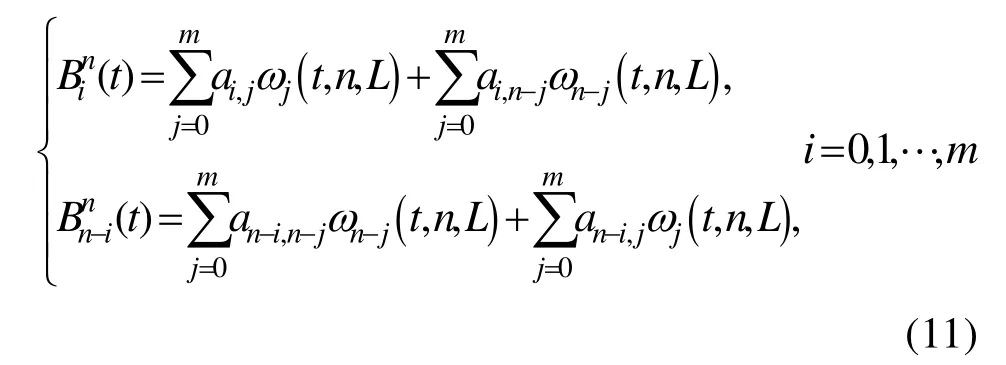
其中,①0≤j≤m-L,

②m-L+1≤j≤ m,
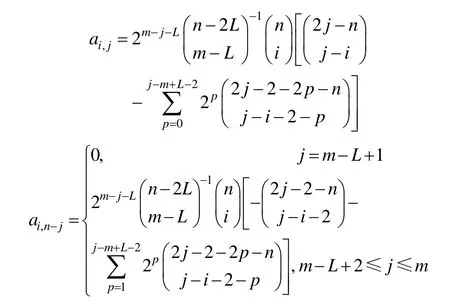
(2) 当n=2m时,

其中,①0≤j≤m-L,

②当m-L+1≤j≤m时,
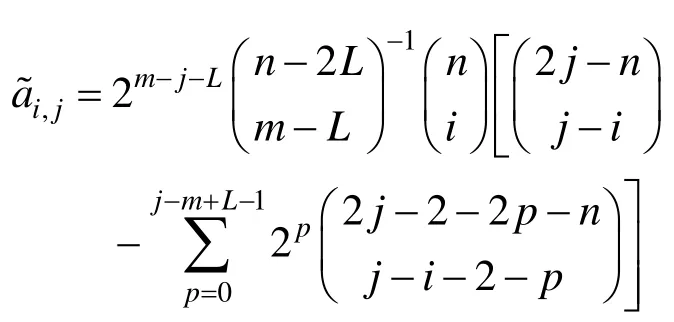
当m-L+1≤j≤ m-1时,
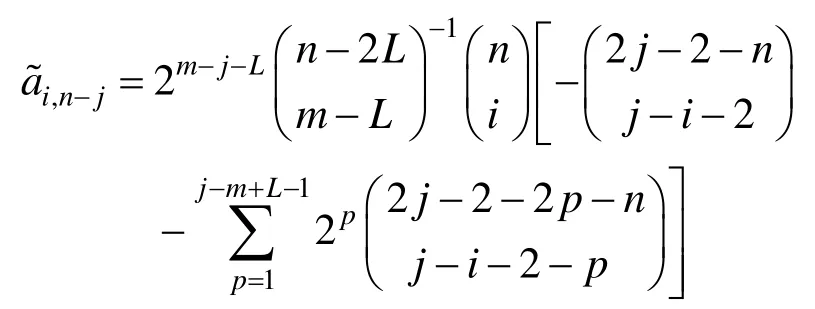
有了以上基转换公式,就可以实现一条WBGB曲线由Bézier曲线的形式绘出,反之亦然。
为方便起见,将 n-1次WBGB曲线式(3)升阶为n次曲线,即
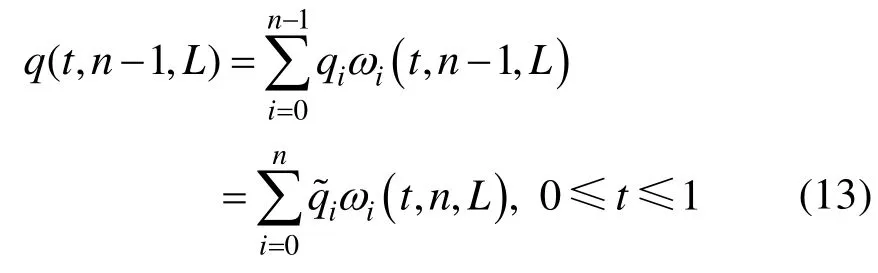
定理 3. 若式(13)中 n-1次多项式 q( t, n-1,L)为式(1)中n次多项式 p( t, n, L)的最佳一致逼近,则
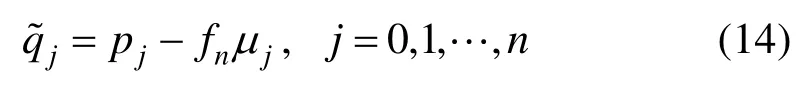
其中
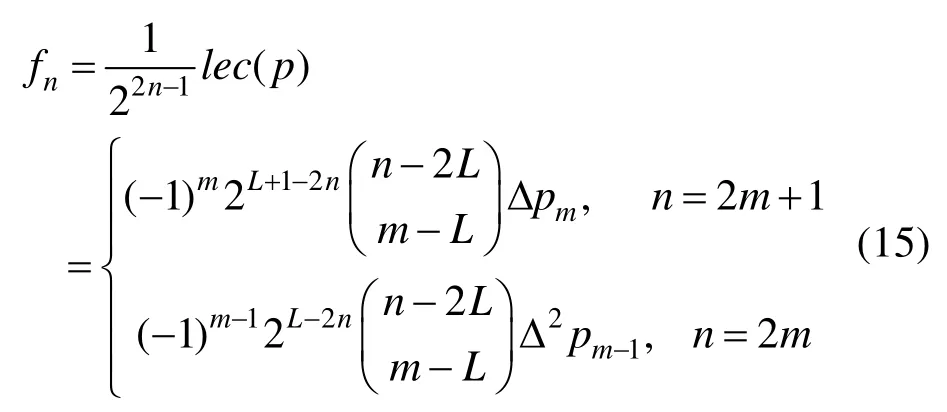
证明. 当 n=2 m+1时,由引理1可得

结合引理2、3,将 Tn(2 t- 1)用WBGB基函数表示,上式即变为
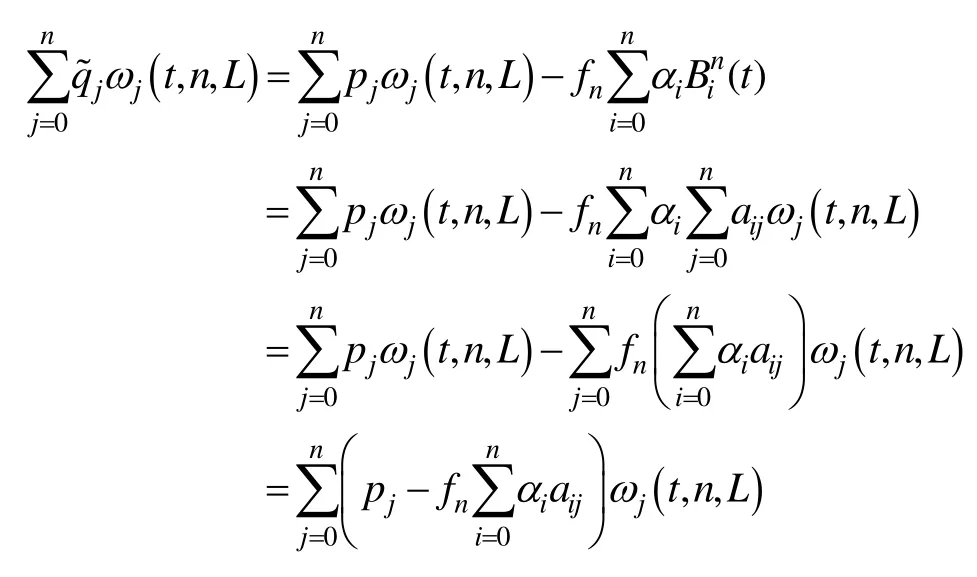
定理 3即为最佳一致逼近法。其较扰动法复杂,但从后文误差分析可看出其逼近效果较扰动法有很大提高,然而却不插值端点,下面导出插值端点的约束最佳一致逼近降阶方法。
3 误差分析
为刻画降阶曲线对原曲线的逼近程度,定义逼近误差与相对误差分别为
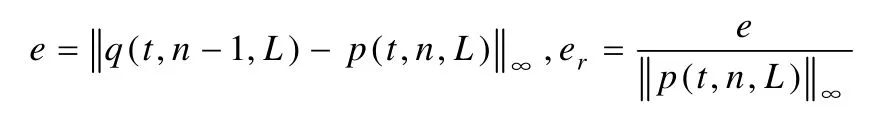
其中
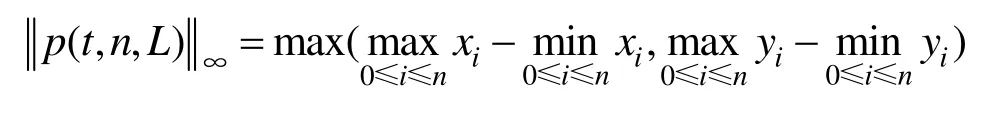
3.1 扰动法误差
定理 4. 扰动法所得降阶曲线 q( t, n - 1,L)与原曲线 p( t, n, L)的逼近误差为

证明. 先讨论 n=2 m+1的情形,由扰动法及式(8),有
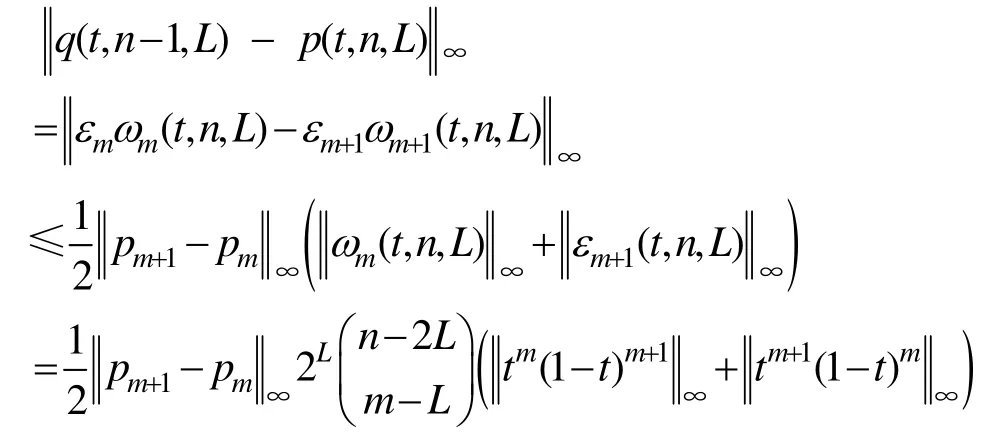
同理可得 n= 2m时结论成立。 证毕。
3.2 最佳一致逼近法误差
定理 5. 最佳一致逼近法所得降阶曲线q( t, n - 1,L)与原曲线 p( t, n, L)的逼近误差为

4 数值实例
例1给定一条6次WBGB曲线 p( t, 6,1),其控制顶点为{(210,110),(170,220),(190,360),(260,410), (355,425),(470,320),(430,110)}。
利用扰动法对其降一阶后得到的5次WBGB曲线的控制顶点为{(210,110),(156.6667,256.6667), (185.8333,365.8333),(469.1667,572.5000),(483.3333, 390.0000),(430,110)}。图 2为 6次 WBGB曲线p( t, 6,1),当 L=1时的降阶前后的图形,其中原曲线和原控制多边形用实线表示,降阶后的曲线和控制多边形用虚线表示,其降阶误差为6.562 5。
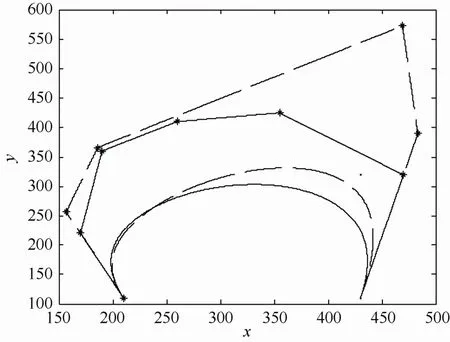
图2 6次WBGB曲线的降阶(扰动法)
利用最佳一致逼近法对其降一阶后得到的 5 次WBGB曲线的控制顶点为{(208.8800,111.5683), (162.8375,248.0254),(183.9610,368.4563),(348.9610, 433.4563),(489.5041,381.3592),(428.8800,111.5683)}。
图3为6次WBGB曲线 p( t, 6,1),当 L= 1时的降阶前后的图形,其中原曲线和原控制多边形用实线表示,降阶后的曲线和控制多边形用虚线表示,其降阶误差为0.1025。
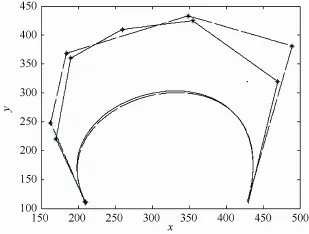
图3 6次WBGB曲线的降阶(最佳一致逼近法)
例2给定一条7次WBGB曲线 p( t, 7,L),其控制顶点为{(230,110),(170,230),(190,350),(260,400), (355,425),(470,320),(490,240),(430,100)}。
利用扰动法对其降一阶后得到的6次WBGB曲线的控制顶点为{(230,110),(170,230),(190,350), (307.5,412.5),(470,320),(490,240),(430,100)}。图4 为7次WBGB曲线 p( t, 7,L),当 L=1和 L= 3时降阶前后的图形,其中原曲线和原控制多边形用实线表示,降阶后的曲线和控制多边形用虚线表示,其误差分别为29.687 5和11.875 0。
利用最佳一致逼近法对其降一阶后得到的 6 次WBGB曲线的控制顶点,当 L= 1时为{(224.2512,98.4878),(196.6600,237.0128),(145.8949, 338.3984),(294.8198,409.1592),(514.1051,331.6016), (463.3400,232.9872),(435.7488,101.5122)};当 L=3时降阶后的控制顶点为{(219.3535,91.2007), (204.4126,239.0481),(145.8759,338.3984),(294.8348, 409.1592),(514.1241,331.6016),(455.5874,230.9519), (440.6465,102.7993)}。图 5为 7次 WBGB曲线p( t,7, L),当 L=1和 L= 3时降阶前后的图形,其中原曲线和原控制多边形用实线表示,降阶后的曲线和控制多边形用虚线表示,其误差分别为0.231 9和0.092 8。

图4 7次WBGB曲线的降阶(扰动法)

图5 7次WBGB曲线的降阶(最佳一致逼近法)
实际上,p ( t, 7,3)即为Wang-Ball曲线,文献[12]利用曲线升阶和降阶的关系给出了 Wang-Ball曲线的一种降阶方法。通过计算发现,与本文扰动法降阶后得到的曲线是一致的,但是误差不如最佳一致逼近法的小,这说明本文的方法还是有效的。
从以上数据及图形还可以看出来,扰动法和最佳一致逼近法,当n固定时,L的值越大,降阶效果越好。
5 结 论
本文分别利用扰动法和最佳一致逼近法给出了WBGB曲线的降阶算法。实验结果表明,从逼近效果而言,用最佳一致逼近法效果比扰动法要好,若利用扰动法得到的降阶曲线不能达到预期的误差,则可以先利用细分算法对曲线做细分,再逐段用扰动法降阶;利用扰动法对 n( n ≥ 3)次的WBGB曲线降阶所得曲线插值端点,而最佳一致逼近法降阶所得曲线不插值端点;扰动法计算耗时要比最佳一致逼近法少。值得一提的是,本文是在 WBGB曲线的位置参数1≤L≤m(此时WBGB曲线包含 Wang-Ball曲线以及介于 Bézier曲线和 Wang-Ball曲线之间的一些中间曲线)的前提下进行的,因为位置参数 L=0时(此时 WBGB曲线即为Bézier曲线),精确降阶条件并不成立,因此本文的降阶方法对Bézier曲线并不成立。
[1] Ball A A. CONSURF, Part 1: Introduction to conic lofting title [J]. Computer-Aided Design, 1974, 6(4): 243-249.
[2] Ball A A. CONSURF, Part 2: Description of the algorithms [J]. Computer-Aided Design, 1975, 7(4): 237-242.
[3] Ball A A. CONSURF, Part 3: How the program is used [J]. Computer-Aided Design, 1977, 9(1): 9-12.
[4] Said H B. A generalized Ball curve and its recursive algorithm [J]. ACM Transactions on Graphics, 1989, 8(4): 360-371.
[5] 王国瑾. 高次Ball曲线及其几何性质[J]. 高校应用数学学报: A辑, 1987, 2(1): 126-140.
[6] 王成伟. 三次 Ball曲线的扩展[J]. 工程图学学报, 2008, 29(1): 77-81.
[7] 王成伟. 四次 Wang-Ball曲线的扩展[J]. 工程图学学报, 2009, 30(1): 80-84.
[8] 严兰兰, 梁炯丰, 饶智勇. 三次 Ball曲线的两种新扩展[J]. 工程图学学报, 2011, 32(5): 20-24.
[9] 严兰兰, 张 文, 温荣生. 两类形状可调五次广义Ball曲线[J]. 工程图学学报, 2011, 32(6): 16-20.
[10] Wu H Y. Unifying representation of Bézier curve and generalized Ball curves [J]. Applied Mathematics: A Journal of Chinese Universities (Series B), 2000, 15(1): 109-121.
[11] 汪志华, 朱晓临. Bézier曲线与Wang-Ball曲线的统一表示[J]. 计算机辅助设计与图形学学报, 2008, 20(7): 888-893.
[12] Hu S M, Wang G Z, Jin T G. Properies of two types of generalized Ball curves [J]. Computer-Aided Design, 1996, 28(2): 125-133.
[13] 江 平, 檀结庆. Wang-Said型广义 Ball曲线的降阶[J]. 软件学报, 2006, 17(增刊): 93-102.
[14] 刘 刚, 王国瑾. Said-Bézier型广义Ball曲线显示降多阶[J]. 软件学报, 2010, 21(6): 1473-1479.
[15] Brunnett G, Schreiber T, Braun J. The geometry of optimal degree reduction of Bézier curves [J]. Computer Aided Geometric Design, 1996, 13(8): 773-788.
[16] Zhang L, Wu H Y, Tan J Q. Dual bases for Wang-Bézier basis and their applications [J]. Applied Mathematics and Computation, 2009, 214(1): 218-227.
Degree Reduction of Wang-Bézier Generalized Ball Curves
Wang Yan1, Li Zhim ing2
(1. School of Mathematics and Statistics, Hefei Normal University, Hefei Anhui 230601, China; 2. School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China)
The degree reduction of generalized Ball curves of Wang-Bézier type is discussed by perturbation and the best uniform approximation respectively. The approximation error is given. The experimental results demonstrate that the effect of the best uniform approximation is better than that of perturbation. If the error cannot be obtained in advance, the original curve can be subdivide firstly, and then reduce the degree by using of perturbation part by part. The degree reduction method of WBGB curves enriches the theory system of generalized Ball curves effectively.
WBGB curves; perturbation method; best uniform approximation
TP 391.72
A
2095-302X(2016)04-0476-07
2015-11-26;定稿日期:2016-01-20
国家自然科学基金项目(60773043,61070227);教育部科学技术研究重大项目(309017);合肥师范学院人才科研启动基金项目(2014rcjj05)
王 燕(1985–),女,山东泰安人,讲师,博士。主要研究方向为计算机辅助几何设计。E-mail:wy030515@163.com

