铝制毛坯筒形件双轮强力旋压仿真模型的建立

杨羽

（长春理工大学 生命科学技术学院，长春 130022）

铝制毛坯筒形件双轮强力旋压仿真模型的建立

杨羽

（长春理工大学 生命科学技术学院，长春 130022）

部分筒形铝制毛坯在强旋过程中需要利用尾顶将其顶紧在芯模上，但由于毛坯较软以及所需顶紧力较大等原因，导致尾顶嵌入毛坯，使毛坯件发生轻微变形的现象，毛坯的局部变形会造成减薄量的改变，从而导致旋压工艺参数设置的偏差，最终使旋压制品的尺寸精度难以保证，需要经过反复的旋压工艺实验修正工艺参数才能使最终的成形制品达到设计要求。提出了一种尾顶力的计算方法，并利用该算法对毛坯进行加载，利用修正的Thamasett算法建立毛坯与旋轮的关系，从而以Ansys为平台建立了一个针对铝制毛坯的筒形件双轮强力旋压仿真模型。利用旋压工艺实验对仿真模型进行验证，其结果与仿真结果一致。该仿真模型可用于指导旋压生产企业的生产，可为企业节约大量的毛坯实验件成本以及旋压工艺实验时间。

铝制毛坯；筒形件；强力旋压；尺寸精度

筒形件双轮强力旋压加工是指毛坯装卡在芯模上并随芯模旋转，同时利用两个对称旋压工具绕毛坯旋转，两个旋压工具与芯模之间相对进给，使毛坯受压并产生连续的局部塑性变形，从而获得空心回转零件的塑性加工过程［1］。

筒形件双轮强力旋压在国防工业以及民用工业方面都得到了广泛的应用。比如火箭弹壳体、气瓶等［2-7］。铝制旋压制品在各行各业的应用也逐渐增多，但随着对旋压制品尺寸精度的要求越来越高，尾顶力对铝制毛坯挤压变形所造成的影响越来越引起旋压生产企业的关注。

铝制毛坯在筒形件双轮强力旋压过程中，需要利用尾顶将铝制毛坯顶紧在芯模上，其顶紧力的大小必须足够，若顶紧力过小，则在旋压过程中毛坯在旋压力和离心力的作用下会发生相对转动，甚至可能将毛坯从工作区中抛出造成事故。若顶紧力过大，则会引起主轴和尾顶的轴承过载。但即使是大小适中的顶紧力依然会对铝制毛坯会造成一定量的变形。最直观的表现就是尾顶嵌入铝制毛坯，并且在嵌入部分的周边形成一定的变形量。这就改变了毛坯的减薄量，从而使得设定的旋压工艺参数产生偏差，进而影响整个旋压制品的尺寸精度，尤其是接近尾顶位置的尺寸精度。

目前国内外的旋压企业所采用的应对方法均是先忽略掉尾顶力对铝制毛坯所造成的变形，设定旋压工艺参数并且进行旋压工艺实验，依据实验结果与设计指标的偏差再修正旋压工艺参数，并再次进行旋压工艺实验，如此往复，直至旋制出合格的旋压制品。但这种方法会造成大量的旋压毛坯实验件的浪费，并且每次旋压均需要调整旋压工艺参数，其调整周期非常耗时。通常情况下每旋制一个新的铝制旋压制品，需要进行5次左右的旋压工艺实验，每次旋压工艺实验大约要消耗掉3个铝制毛坯，每次工艺实验后调整工艺参数的周期为2天左右，一共需要消耗至少10天以上才能完成一个新的铝制毛坯的工艺参数的摸索。

论文提出了一种尾顶力的计算方法，并利用该算法对毛坯进行加载，利用修正的Thamasett算法建立毛坯与旋轮的关系，从而以ANSYS为平台建立了一个针对铝制毛坯的筒形件双轮强力旋压仿真模型。

1 尾顶力算法

尾顶主要由电机、窄V带、顶轴、顶料盘、丝杠、箱体等几部分组成。工作时，由电机通过窄V带带动丝杠旋转，使顶轴纵向进给，直到顶轴前端的顶料盘将毛坯与芯模固定好。在旋压过程中，顶轴随毛坯和芯模同步转动。旋压结束后，顶轴带动顶料盘纵向退回。

对尾顶力的计算是以保证在旋压过程中毛坯相对芯模处于静止状态为目的。毛坯与芯模间的摩擦力可利用库仑定律来确定。

将作用于毛坯上所有力转化到旋转中心O上，那么作用于毛坯上的力系总矢量的投影为:

式中，Q为顶紧力；PZ为旋压力轴向分力；PN为芯模表面上所有反力的法向分力的合力；Pr为旋压力径向分力；PμY为摩擦力总矢量在Y方向上的投影；Pl为旋压力切向分力；PμX为摩擦力总矢量在X方向上的投影。

作用在毛坯上的力系总力矩投影为:

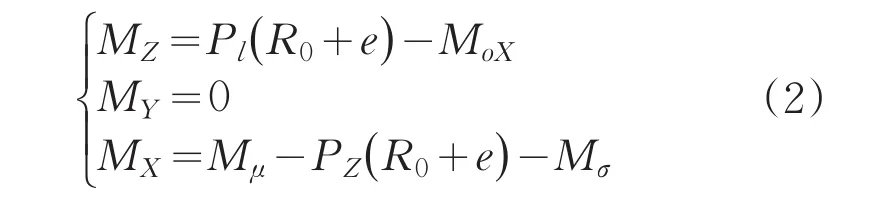
式中，R0为芯模半径；e为旋压力作用点至芯模母线的距离；M0X相对X轴芯模的反力矩；Mμ为相对Z轴的摩擦力矩；Mσ阻止顶紧块转动的力矩。

保证毛坯相对芯模静止的必要和充分条件是，作用其上力系的总矢量与总力矩都要等于零。因此有:

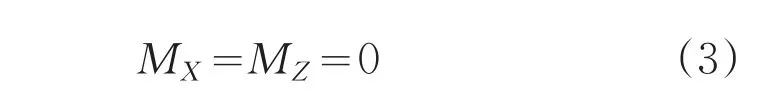
若使毛坯处于相对静止状态，那么摩擦力矩必须等于或大于外力矩，则:

因此得出Mμmax与作用力之间的关系。假设作用于毛坯与芯模的接触面上无穷小单位面积的摩擦力为:式

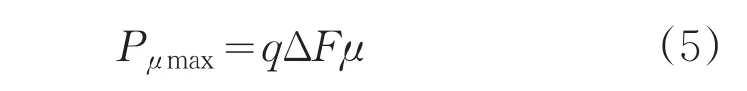
中，q为作用单元面积上的正压力；ΔF为毛坯的单元面积；μ为摩擦系数，与毛坯和芯模接触表面状态有关。

Pμmax垂直于单元面积，同时又是至接触表面中心O点的向径。则:

其中，qi可以表示为:

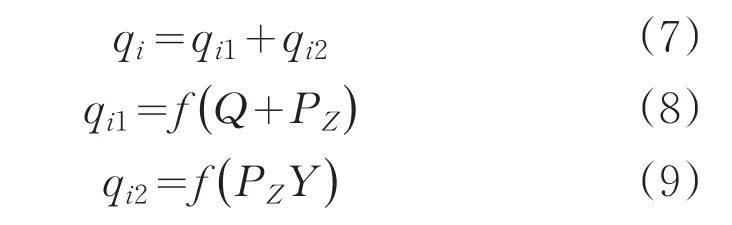
可以认为毛坯和芯模接触表面上每点qi1是相同的，而qi2与各点到Z轴的距离成正比。

作用于单元接触面上的力qi2相对X轴的力矩为:

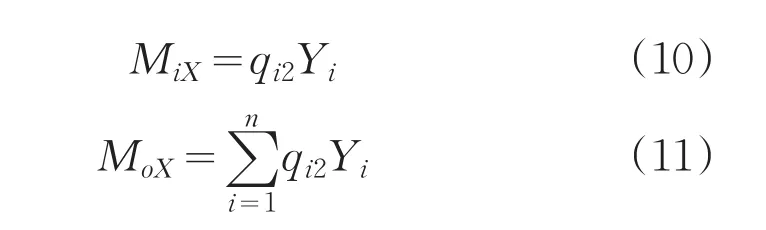
以极坐标(r,ϕ)来表示:

式中，λ为未知的比例系数；dF为单元面积。

则相对X轴力矩:

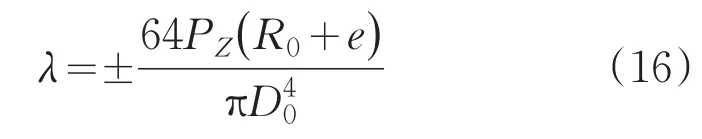
当0≤ϕ≤π时，λ取正值；当π≤ϕ≤2π时，λ取负值。

因此qi可表示为:

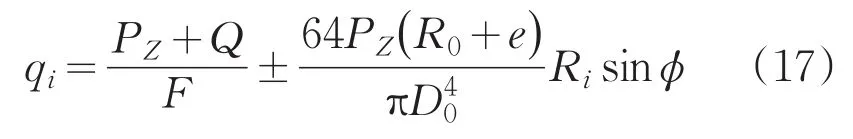
未知比例系数为:

单位面积上最大摩擦力对回转中心的力矩为:

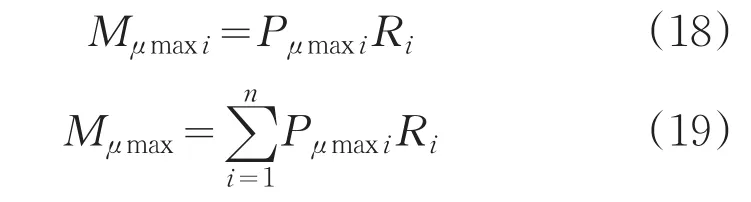
如果i→∞，ΔF→0，则:

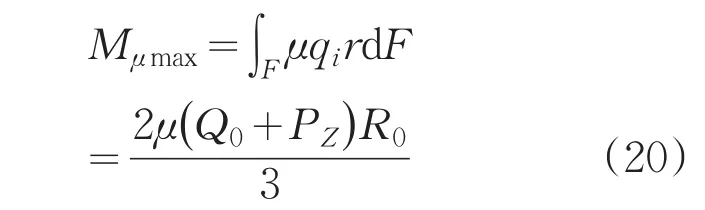
尾顶的顶紧力为:

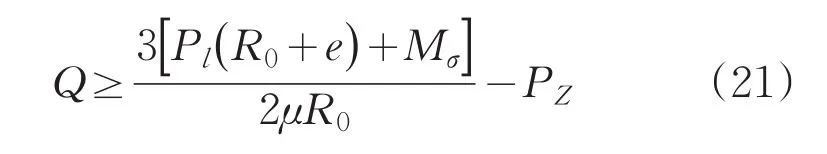
以直径100mm铝制毛坯为例，分析尾顶力对毛坯减薄量所产生的影响。其实验参数如表1所示。

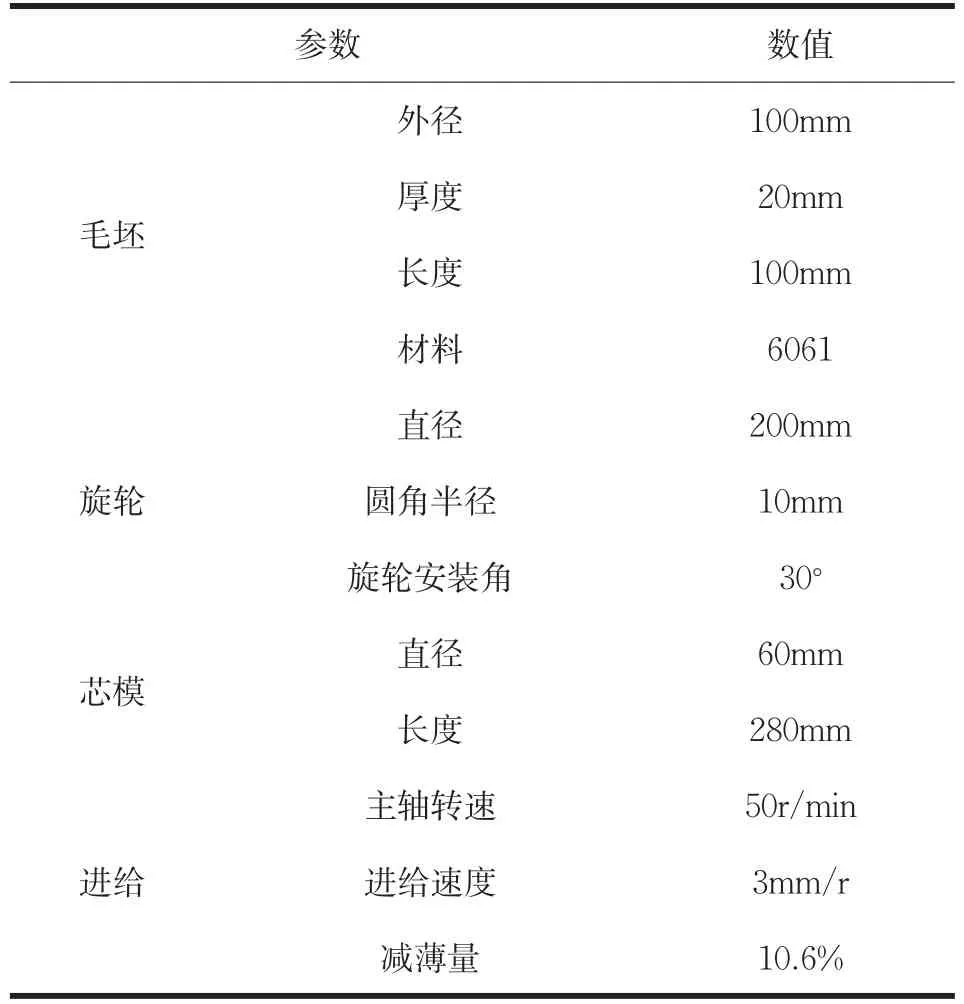
表1 实验参数

通过建立有限元模型进行分析，可得到以下结果:在顶紧力作用下，铝制毛坯在径向最大变形量为0.047mm，如图1所示。

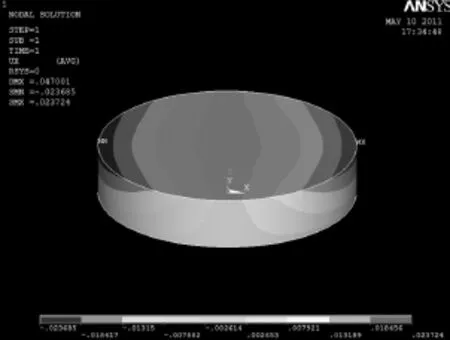
图1 毛坯径向变形量

所以在靠近尾顶位置毛坯的最大变形量应为10.647mm，要大于预计的减薄量10.6mm，减薄量的变化会直接导致旋轮旋压力的改变。所以有必要建立准确的旋压力算法，以保证准确的旋压工艺参数的设定。

2 旋压力算法

通常情况下旋压生产企业会使用Thamasett算法对筒形件旋压力进行计算。但通过大量的旋压工艺实验发现，其实验电测法所测得的旋轮旋压力与Thamasett算法所求取的旋轮旋压力存在偏差。Thamasett算法所求取的旋压力相较于测得值，在径向上的偏差约为15%，在轴向上的偏差约为25%，在切向上的则偏差约为200%。根据这一规律，对Thamasett算法进行参数修正。则旋轮所受径向力为［8］:

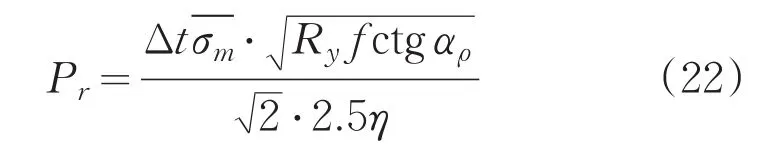
旋轮所受轴向力为:

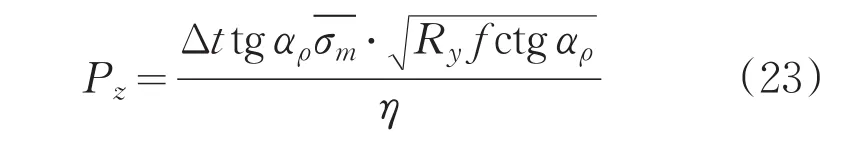
旋轮所受切向力为:

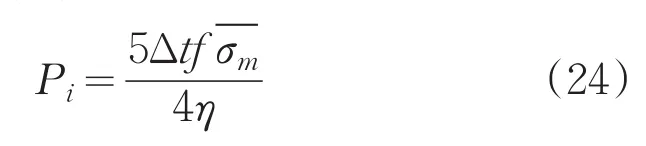
3 仿真模型建立

以算法作为基础，可以建立仿真模型，然后对旋压过程及其结果进行模拟。其旋压成形参数如表2所示。

表2 旋压成形参数

首先利用CATIA建立几何模型，如图2所示。

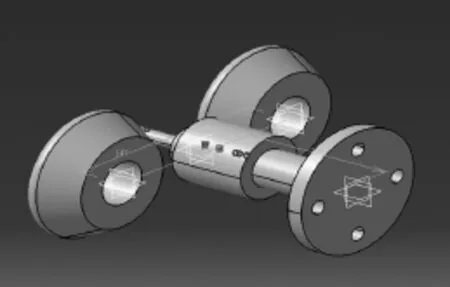
图2 几何模型

利用Hypermesh对几何模型进行前处理，如图3所示。

图3 Hypermesh前处理

以Ansys为平台对算法进行二次开发，并且建立尾顶与毛坯、旋轮与毛坯的接触。其实验条件如表1所示，旋压工艺参数如表3所示。

表3 旋压工艺参数

利用Ansys进行求解，求得旋轮的塑性变形分别如图4、图5、图6所示。

图4 方案1毛坯塑性变形

图5 方案2毛坯塑性变形

图6 方案3毛坯塑性变形

4 旋压工艺实验

为了便于与动力学仿真模拟的结果进行对比，论文的工艺实验仍然选择与仿真相同的铝制毛坯作为实验材料，实验所用设备为QX62系列双旋轮强力旋压机，如图7所示。其实验结果如表4所示。

图7 双旋轮强力旋压机

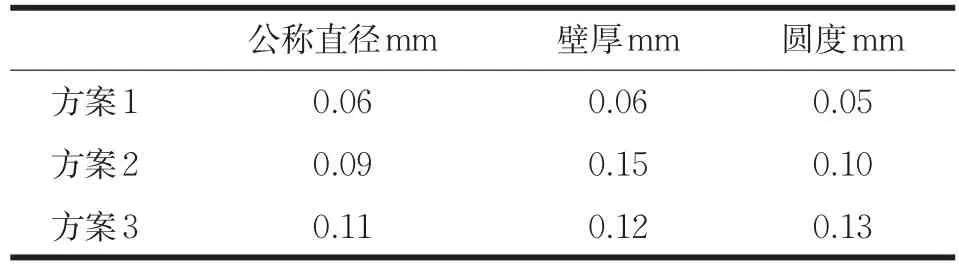
表4 实验结果

5 成形结果对比分析

方案1、方案2、方案3的仿真结果与工艺实验旋压制品对比如图8、图9、图10所示。

图8 方案1仿真模型与旋压制品对比

图9 方案2仿真模型与旋压制品对比

图10 方案3仿真模型与旋压制品对比

方案1的仿真成形过程一直较为稳定，没有出现裂纹或者扩径的趋势，成形质量较好。从旋压制品工艺实验结果来看，其塑性变形过程与仿真相符，其旋压制品实验结果与设计要求相符。

方案2的仿真过程中毛坯出现了较深的纹理，有破裂的倾向。从旋压制品工艺实验结果来看，由于进给量过大，最终导致毛坯出现裂纹。

方案3的仿真过程出现了明显的不贴膜现象。从旋压制品工艺实验结果来看，由于主轴转速过高，其旋压制品的确出现了不贴膜的现象。

6 旋压力结果对比分析

旋压力是否准确也是验证旋压仿真模型是否准确的重要依据，利用电测法可以准确的测量旋压过程中轴向、径向和切向的旋压力。其测量结果如表5所示。

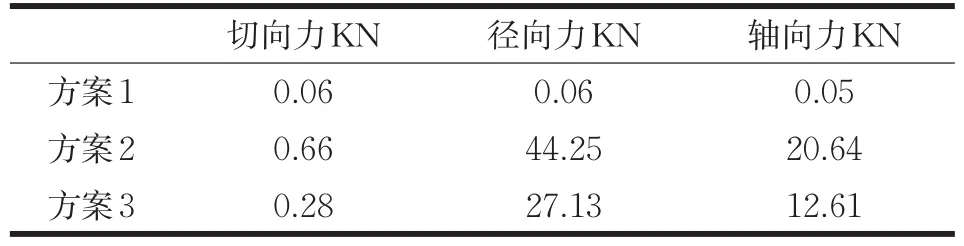
表5 实验结果

仿真模拟所得到的方案1、方案2、方案3的受力分别如图11、图12、图13所示。

图11 方案1轴向力、径向力、切向力

图12 方案2轴向力、径向力、切向力

图13 方案3轴向力、径向力、切向力

从对比结果来看，方案1、方案2、方案3的模拟旋压力与电测法测量所获取的旋压力基本相符。

7 结论

论文以Ansys为平台建立了针对铝制毛坯的筒形件双旋轮强力旋压仿真模型。并通过旋压工艺实验验证了模型的准确性。该模型可用于旋压生产企业的生产，可为企业节约大量的毛坯实验件成本以及旋压工艺实验时间。

［1］ 杨羽.筒形件强力旋压动力学仿真研究［D］.长春:长春理工大学，2014.

［2］ 路平，张云开，陈波.汽车轮辐错距强力旋压成形的有限元仿真［J］.上海交通大学学报，2015，49（1）:56-61.

［3］ 缪伟亮，刘大海，邵雪明.工艺参数对薄壁件多道次旋压变形均匀性的影响［J］.精密成形工程，2014，6（2）: 18-23.

［4］ 张行健，阴中炜，周晓建，等.大直径6061铝合金筒形件旋压工艺及性能研究［J］.轻合金加工技术，2013（10）: 54-58.

［5］ 李启军，范开春，王琪，等.大尺寸薄壁钛合金筒体旋压成形质量影响因素［J］.宇航材料工艺，2012，42（1）: 86-88.

［6］ 李克智，李贺军，吕炎.筒形旋压件内径尺寸精度预测［J］.航空工艺技术，1998（5）:11-13.

［7］ 张学光，张治峰，梁嵬，等.筒形件旋压加工中材料隆起情况分析研究［J］.长春理工大学学报:自然科学版，2016，39（1）:56-60.

［8］ 杨羽，曹国华.筒形件旋压力Thamasett算法参数修正及仿真［J］.兵器材料科学与工程，2012，35（1）:84-87.

Establishment of Simulation Model of Aluminum Alloy Blank Cylindrical Pieces by Spinning Power

YANG Yu
（School of Life Science and Technology，Changchun University of Science and Technology，Changchun 130022）

Some of the cylindrical aluminum alloy blank need to be topped tightly with the end of the top in the spinning process.The soft blank and the larger top tight force lead to the end of the top embedding the blank and slight deformation of blank.The local deformation of blank will cause the change of thickness deduction and the deviation of spinning process parameter.Dimensional accuracy of spinning products is hard to guarantee.Only by repeated spinning process experiment to correct the process parameter，the final products can meet the design requirement.This article proposes a calculation method of the top end force and exert it upon the blank and establish a simulation model of aluminum alloy blank cylindrical pieces based on Ansys.The result is in accordance with the simulation one by the simulation experiment.The simulation model can be used for guiding spinning production and save a lot of blank experiment cost and spinning process experiment time.

aluminum alloy blank；cylindrical pieces；power spinning；dimensional accuracy

TH164

A

1672-9870（2016）05-0076-05

2016-05-16

杨羽（1983-），男，博士，讲师，E-mail:yangyu1983@sina.com