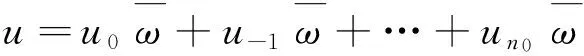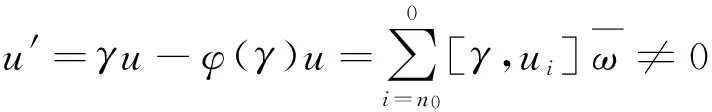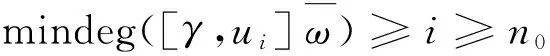无中心W-代数NW(2,2)的Whittaker模

于亚峰

(贵州师范大学 数学与计算机科学学院,贵州 贵阳 550001)



无中心W-代数NW(2,2)的Whittaker模

于亚峰

(贵州师范大学 数学与计算机科学学院,贵州 贵阳 550001)

给出了无中心W-代数NW(2,2)的Whittaker模的定义，并得到了无中心W-代数NW(2,2)的Whittaker模的一些基本性质。

无中心W-代数NW(2,2)；Whittaker向量；Whittaker模

0 引言

D.Arnal和G.Pinzcon在1974年首次定义了关于Sl2(c)的Whittaker模[1]。后来B.Kostant给出了所有有限维复半单李代数的Whittaker模，并证明了有限维复半单李代数的Whittaker模与其泛包络代数的理想之间存在一一对应[2]。

一个有限维复半单李代数g的Whittaker模依赖于g的三角分解：g=g-⊕H⊕g+，而每一个Whittaker模则依赖与一个给定的非奇异泛函ψ:g+→。关于复半单李代数Whittaker模的结果已经被推广到其他有着类似结构的代数上，比如：2000年Sevoystanov给出了关于Un(g)的Whittaker模[3]，Ondrus在2005年给出了Uq(Sl2)的Whittaker模[4]。而关于广义Weyl代数的Whittaker模则由Benkart和Ondrus在2009年给出[5]。同年M.Ondrus和E.Wiesner讨论了Virasoro代数的Whittaker模[6]。在[7]中，Christodoupoulou研究了无扭仿射李代数的Whittaker模。

Virasoro代数的表示在数学、物理的众多分支(如:共形场论、可积系统、顶点算子代数等)都有重要的应用,是无限维李代数表示理论的重要课题。由于Whittaker模在李代数表示理论的研究中起着重要作用，所以越来越受到人们的关注，如文献[8,9]。

本文将给出无中心W-代数NW(2,2)的Whittaker模的定义，并研究其一些基本的性质。

1 无中心W-代数NW(2,2)的Whittaker模

W(2,2)作为Virasoro代数的扩张,有着很好的最高权模理论，由其最高权模可以得到一类新的顶点算子代数，因此对W(2,2)的表示理论的研究有着重要的意义和价值。

W-代数W(2,2)是一个无限维李代数，具有基{Lm,Gm,c|m∈}，其中c是中心元，且对任意的m,n∈，其换位运算定义为：

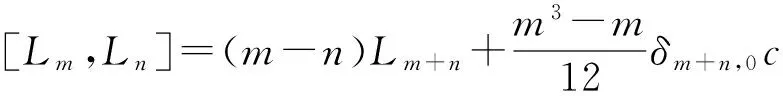
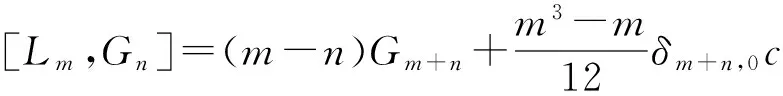
[Gm,Gn]=0。

因为L0的伴随作用是半单的，所以W(2,2)是一个-阶化代数，且有三角分解：

W(n)=L-n⊕G-n, n≠0

W(0)=L0⊕G0⊕c,

W(2,2)=W+⊕W0⊕W-,

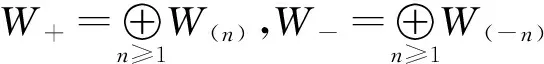
现在我们去掉中心元c，则无中心W-代数NW(2,2)具有基{Lm,Gm|m∈}，且对任意的m,n∈，其换位运算定义为：

[Lm,Ln]=(m-n)Lm+n,

[Lm,Gn]=(m-n)Gm+n,

[Gm,Gn]=0。

NW(n)=L-n⊕G-n, n≠0

NW(0)=L0⊕G0,

NW(2,2)=NW+⊕NW0⊕NW-,

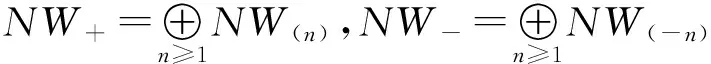
类似文献[8]，对一个有限维的非递减的整数序列λ=(λ1，…,λt),(λ1≤λ2≤…≤λt)，称之为一个划分。记所有划分构成的集合为P。对λ=(λ1，…,λt)∈P,若所有λi>0，1≤i≤t，则称λ是一个正划分，若所有的λi≥0，1≤i≤t，则称λ是一个非负划分。 所有正划分构成的集合记为P>0，而所有非负划分构成的集合记为P≥0。定义λ的长度为t，记作l(t)。

对λ=(λ1，…,λt)∈P≥0,k∈,k≥0，记λk为正整数k在划分λ中出现的次数，且当k充分大时，λk=0。显然λk由划分λ完全决定。因此，我们有时也把λ写作λ=(0λ(0)1λ(1)…)。 现在设Lλ,Gλ,L-λ,G-λ∈U(NW(2,2))，则定义

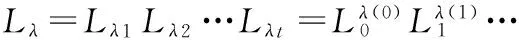
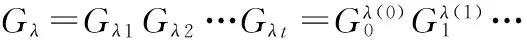
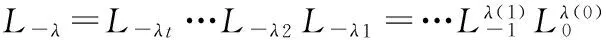
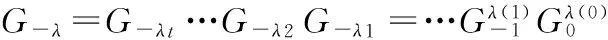
其中λ∈P≥0。设0=(0010…)，且L0=G0=1∈U(NW(2,2))，规定0属于P≥0，但0不属于P>0。

由PBW定理可知，{L-λG-λ′LμGμ′|λ,λ′∈P≥0,μ,μ′∈P>0}是U(NW(2,2))的一组基，由于NW(2,2)是一个-阶化代数，所以U(NW(2,2))也是一个-阶化代数，即

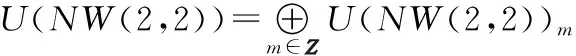
其中U(NW(2,2))m=Span。

容易验证U(NW(2,2))mU(NW(2,2))n⊂U(NW(2,2))m+n。

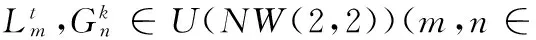
下面类似于文献[3]，定义NW(2,2)的Whittaker模。

定义1 设φ：NW+→C是一个李代数同态，若φ(L1),φ(L2),φ(G1),φ(G2)都不为0，则称φ是非奇异的。否则称φ是奇异的。对一个NW(2,2)模V,设v∈V,若对所有的α∈NW+都有αv=φ(α)v，则称v是一个Whittaker向量。而且若V是由v生成的，则称V是NW(2,2)的一个φ型Whittaker模。(这里要求φ是非奇异的。)

对于一个给定的非奇异的φ，定义一个一维的NW+-模φ,即∀α∈NW+,a∈,αa=φ(α)a，则立即可得到一个φ型Whittaker模

Mφ=U(NW(2，2))⊗U(NW+)φ。

2 无中心W-代数NW(2,2)的Whittaker模的一些基本性质

U(NW(2,2))=U(NW≤0)⊗U(NW+)，

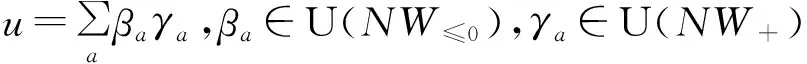
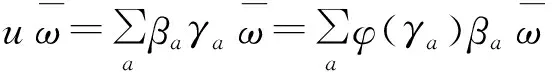
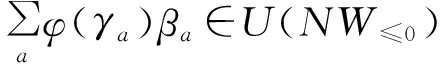
唯一性是显然的。

命题2 设M是一个φ型Whittaker模，ωm是其一个Whittaker向量。若对任一φ型Whittaker模V，ωv是其一个Whittaker向量，都存在一个满同态σ:M→V，使得σ(ωm)=ωv，则M≅Mφ。

证明 由命题3.1可直接得证。

Mφ=M0⊕M-1⊕M-2⊕…。

若0≠v∈Mk，则称v在Mk中是一个k阶非零齐次向量。

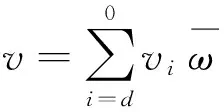
引理1

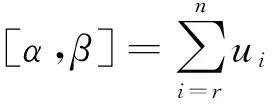
2)设α∈(NW+)n,则αi,j∈(NW+)i，且当i>0,βi,j≠0时，ht(βi,j)

证明 直接验证即可。

命题3 设V是Mφ的一个子模，则V包含一个非零的Whittaker向量。

[1] ARNAL D,PINCZON G.On algebraically irreducible representation of the Lie algebra[J].J Math Phys,1974,15:350-359.

[2] KOSTANT B.On Whittaker vectors and representation theory[J].Invent Math,1978,48:101-184.

[3] SEVOSTYANOV A.Quamtum deformation of Whittaker modules and the Toda lattice[J].J Math Duke,2000,105(2):211-238.

[4] ONDRUS M.Whittaker modules for Uq(Sl2)[J].J Algebra,2005,289(1):192-213.

[5] BENKART G,ONDRUS M.Whittaker modules for generalized Weyl algebras[J].Represent Theory,2009,13:141-164.

[6] ONDRUS M,WIESENR E.Whittaker modules for the Virasoro algebra[J]. J Algebra Appl,2009,8(3):363-377.

[7] CHRISTODOUPOULOU K.Whittaker modules for Heisenberg algebras and imaginary Whittaker modules for affine lie algebras[J].J Algebra,2008,320:2871-2890.

[8] ZHANG X F,TAN S B.Whittaker modules and a class of new modules similar as Whittaker modules for the Schrödinger-Virasoro algebra[J]. arXiv:0812.3245v1[math.RA].

[9] 尹士超,任斌.Loop-Virasoro代数的Whittaker模的若干基本性质[J].常熟理工学院学报(自然科学版),2011,25(2):11-14.

Whittaker modules of centerlessW-algebraNW(2,2)

YU Yafeng

(School of Mathematics and Computer Science,Guizhou Normal University,Guiyang,Guizhou 550001,China)

In this paper, we define the Whittaker modules of centerless W-algebraNW(2,2), and obtain some basic properties.

centerless W-algebra NW(2,2); Whittaker vectors; Whittaker modules

1004—5570(2016)05-0054-03

2016-05-20

贵州省科技基金资助项目(黔科合J字LKS[2012]13号)

于亚峰(1980-)，男，硕士，副教授，研究方向：李代数，E-mail：yyfeng@gznu.edu.cn.

O153

A