Victor-Carmen混沌系统的投影同步
陈昌忠, 何 平
(四川理工学院 自动化与电子信息学院, 四川 自贡 643000)
Victor-Carmen混沌系统的投影同步
陈昌忠, 何 平*
(四川理工学院 自动化与电子信息学院, 四川 自贡 643000)
基于小增益理论,本文研究了一个新型Victor-Carmen混沌系统的投影同步问题.一个更为一般的达成投影同步的充分条件被推得.数值仿真验证了本文所设计的投影同步的有效性.
Victor-Carmen混沌系统; 投影同步; 小增益理论
[11]中,Victor Grigoras和Carmen Grigoras在线性振荡环节的基础上,通过引入非线性动态,得到了一个新型的混沌系统,如下所示:
(1)
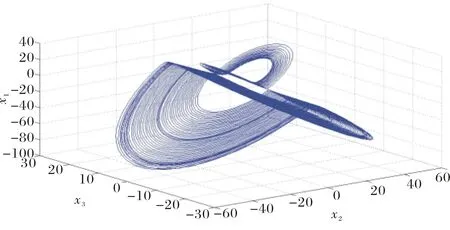
图1 Victor-Carmen混沌系统(1)的相图Fig.1 Phase diagram of the Victor-Carmen chaotic system (1)
其中,x=[x1, x2, x3]T是Victor-Carmen混沌系统的状态变量,a, b, α, β, γ是系统参数.
设定参数a=5, b=9, α=50, β=20, γ=4.1时,系统(1)表现出复杂的混沌性.当取初始条件为x(0)=[5, 1,-5]T时,Victor-Carmen混沌系统(1)的相图如图1所示.
通过计算可得系统的平衡点为
O1(0,0,0)、O2(-0.3468,0.0628,0.01104)、
O3(-2.064,1.382,0.02987)、
O4(0.2500,-0.002231,2'242)、
O5(4.787,2.948,-0.03248).
2 同步控制器设计
将系统(1)看作驱动系统,构造响应系统如下所示.
(2)
定义误差向量
(3)
则误差动力学系统可以写为
(4)
在不同初始条件下,在没有控制器u作用下,响应系统和驱动系统的轨迹将不能达成同步.然而,在合适的同步控制器作用下,响应系统(2)和驱动系统(1)在任何初始条件下达成投影同步,为了实现这一目标,选择控制器如下所示.
(5)
其中,参数k是稍后确定的投影同步控制器增益.
3 主要定理
定理若控制器增益k满足条件
(6)
则驱动系统(1)和响应系统(2)可以在同步控制器(5)的作用下达到关于标量因子η的投影同步,其中ε1和ε2是充分小的正常数,即0<ε1<1,0<ε2<1.
证明将同步控制器(5)代入误差动力系统(4)可得
(7)
根据一阶线性微分方程解的结构易知
e1(t)=exp(-t)e1(0).
(8)
则有

(9)
因此系统(7)可以简化为
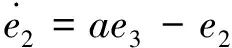
(10-1)

(10-2)
其中,将系统(10-1)、(10-2)看作两个系统的互联形式,将e2和e3分别视为子系统(10-1)的状态和输入,并对其构造Lyapunov函数为

(11)
将Lyapunov函数(11)沿系统(10-1)微分可得
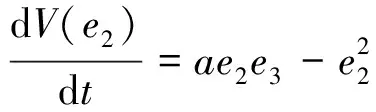
(12)
选择
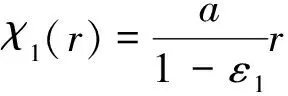
(13)
其中,若ε1(0<ε1<1)是一个充分小的正常数,

(14)
则将(14)式代入(12)式可得

(15)
取K∞函数

(16)
则函数(11)是正则且正定的(proper & positive),因此,函数(11)是系统(10-1)的ISS-Lyapunov函数,系统(10-1)是ISS的,且有

(17)
将e3和e2分别视为子系统(10-2)的状态和输入,并对其构造Lyapunov函数为
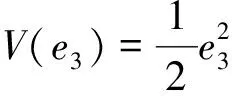
(18)
将Lyapunov函数(18)给系统(10-2)微分可得

(19)
选择
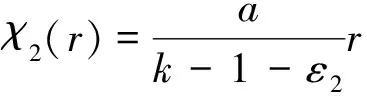
(20)
其中,ε2(0<ε2<1)的一个充分小的正常数.假设

(21)
则有

(22)
同理取K∞函数

(23)
则函数(18)是正则且正定的(proper & positive),函数(18)是系统(10-2)的ISS-Lyapunov函数,系统(10-2)是ISS的,且有
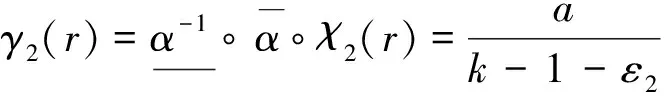
(24)
因此,根据(17)和(24)式可得

(25)
由条件(6)可知
γ2(γ1(r))≤r,∀r>0,
(26)
由小增益定理可知,系统(10)的平衡点是全局渐近稳定的,则有
(27)
由(9)和(27)知,误差系统(7)是全局渐近稳定的,则在同步控制器(5)的条件下,驱动系统(1)和响应系统(2)达成关于标量因子的投影同步.证毕.
4 系统仿真
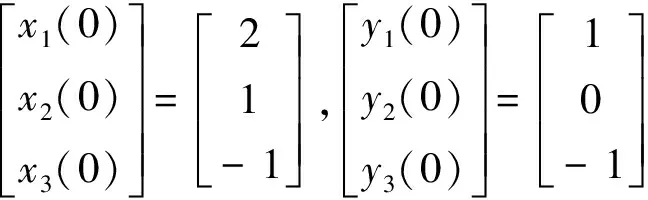
选择标量因子η=3,则初始误差为

驱动系统(1)和响应系统(2)在控制器u的作用下投影同步误差的动态响应曲线如图2-图4所示.
图2~图4 表示了驱动系统(1)和响应系统(2)的投影同步误差,可以看出同步误差很快收敛到零.

图2 驱动系统(1)和响应系统(2)的投影同步误差e1Fig.2 PS error e1of drive system (1) and response system (2)

图3 驱动系统(1)和响应系统(2)的投影同步误差e2Fig.3 PS error e2 of drive system (1) and response system (2)
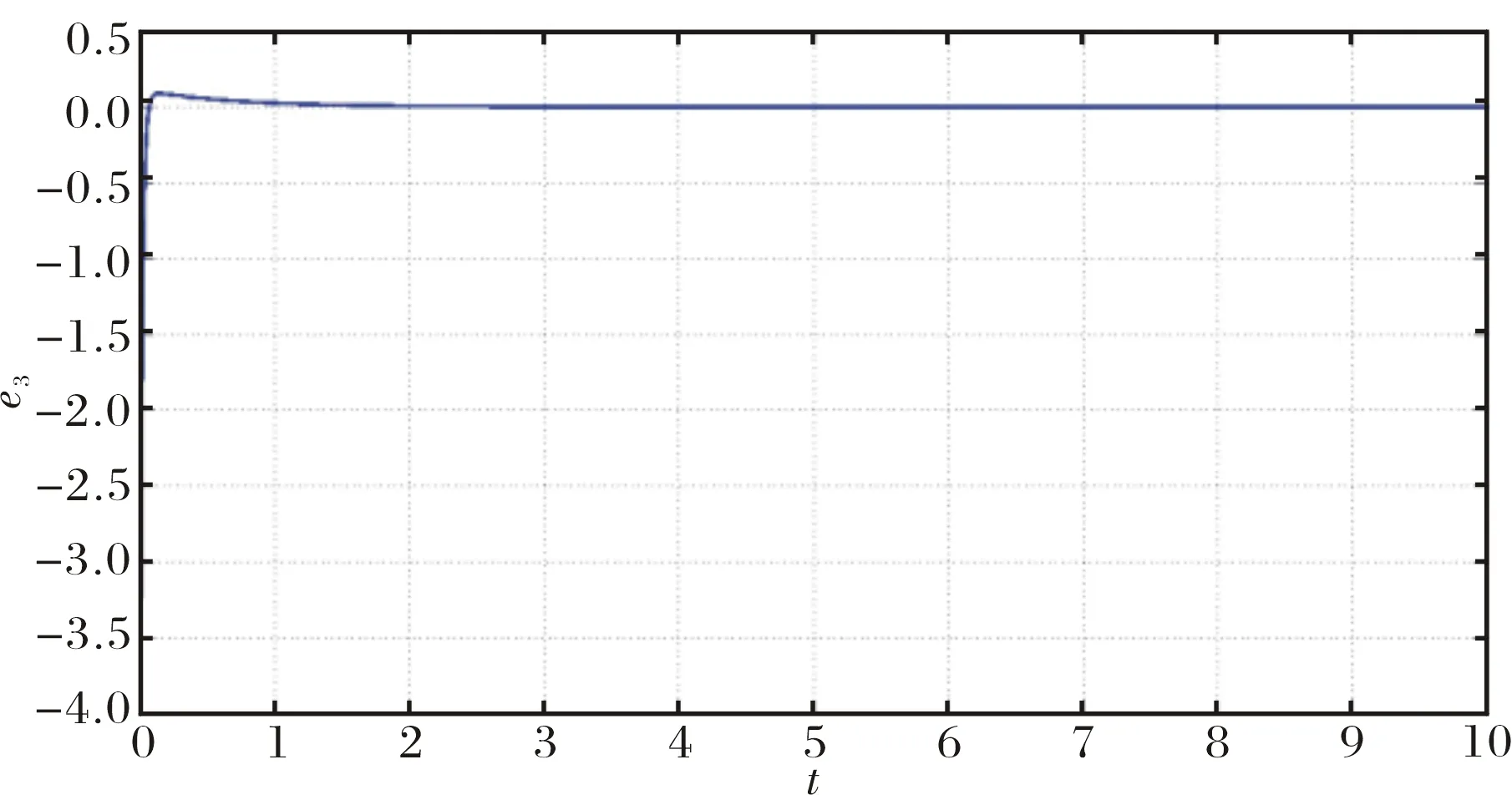
图4 驱动系统(1)和响应系统(2)的投影同步误差e3Fig.4 PS error e3 of drive system (1) and response system (2)
本文的投影同步包含了已有的完全同步和反同步,即,当η=1时,即为完成同步,η=-1时,即为反同步.
5 总结
本文研究了一个新型三维混沌系统的投影同步问题,其创新性在以下两方面:1)简要分析了Victor-Carmen混沌系统的特性;2)基于小增益定理达成了其投影同步问题,包含了反同步与完全同步.最后,数值仿真表明了本文方法的有效性.
参考文献:
[1] BANERJEE R, PADMANABAN E, DANA S K. Control of partial ynchronization in chaotic oscillators[J]. PRAMANA-Journal of Physics, 2015, 84(2): 203-215.
[2] ISRAR A, AZIZAN B S, ADYDA B I, et al. Global chaos synchronization of new chaotic system using linear active control[J]. Complexity, 2014, 21(1): 379-386.
[3] HE P, JING C G, FAN T, et al. Robust decentralized adaptive synchronization of general complex networks with coupling delayed and uncertainties [J]. Complexity, 2014, 19(3): 10-26.
[4] HE P, ZHANG Q L, JING C G, et al. Robust exponential synchronization for neutral complex networks with discrete and distributed time-varying delays: A descriptor model transformation method[J]. Optimal Control Applications and Methods, 2014, 35(6):676-695.
[5] HE P, JING C G, FAN T, et al. Synchronization of general complex networks via adaptive control schemes [J]. PRAMANA-Journal of Physics, 2014, 82(3): 499-514.
[6] HE P, MA S H, FAN T. Finite-time mixed outer synchronization of complex networks with coupling time-varying delay[J]. Chaos, 2012, 22(4): 043151(1-11).
[7] CHEN C Z, FAN T, WANG B R, et al. Feedback linearization synchronization of unified chaotic systems [J]. Journal of Applied Nonlinear Dynamics, 2014, 3(2): 173-186.
[8] FAN T, CHEN C Z, REN X H, et al. Adaptive synchronization of delayed Chen chaotic system[J]. Discontinuity, Nonlinearity and Complexity, 2014, 3(4): 367-378.
[9] 何 平, 任小洪, 李风焕. 不确定性统一混沌系统的鲁棒镇定[J]. 华中师范大学学报(自然科学版) , 2012, 46(1): 35-39.
[10] CHEN C Z, FAN T, WANG B R. Inverse optimal control of hyperchaotic finance system[J]. World Journal of Modelling and Simulation, 2014, 10(2): 83-91.
[11] GRIGORAS V, GRIGORAS C. A Novel Chaotic System for Random Pulse Generation[J]. Advances in Electrical and Computer Engineering, 2014, 14(2): 109-112.
[12] JIAN X. Projective synchronisation of a new chaotic system via small-gain theorem[J]. International Journal of Systems Science, 2012, 43(4): 741-747.
Projective synchronization of the Victor-Carmen chaotic system
CHEN Changzhong, HE Ping
(School of Automation and Electronic Information, Sichuan University of Science & Engineering, Zigong, Sichuan 643000)
The projective synchronization between two identical Victor-Carmen chaotic systems is investigated. Moreover, the general sufficient condition to achieve projective synchronization is obtained by using the small-gain theorem. Numerical simulation is then provided to show the effectiveness and feasibility of the proposed method.
Victor-Carmen chaotic system; projective synchronization; small-gain theorem
2015-11-17.
四川省教育厅基金项目(14ZA0203、14ZB0210);四川理工学院科研基金项目(2014PY14);人工智能四川省重点实验室基金项目(2013RYJ01、2014RYY02);企业信息化与物联网测控技术四川省高校重点实验室开放基金项目(2014WYJ01、2013WYY06).
1000-1190(2016)04-0521-04
O415.5
A
1 Victor-Carmen混沌系统
*通讯联系人. E-mail: pinghe@suse.edu.cn.
过去30年,由于在各个领域的广泛应用,对混沌同步的研究受到了广大学者的亲睐[1-2],相关报道层出不穷[3-6],诸多同步控制方法相继被报道,譬如微分几何方法[7],滑模控制方法[8],鲁棒控制[9],最优控制方法[10]等,这些混沌同步在生物、化学、医药、信息、电子、保密通信等领域中都有广泛应用.在诸多同步体制中,投影同步是最为感兴趣的问题之一.最近,Victor Grigoras和Carmen Grigoras通过在线振荡环节的基础上引入非线性动态,得到了一个新型的三维混沌系统[11],而并没有对其同步问题予以研究.本文则基于小增益定理[12]研究其投影同步问题,从后文的分析可以看出,本文的同步控制器只需要确定额外的一个参数,其分析也是简洁的.

