垂岸式集装箱码头自动化跨运车作业任务分派与序列优化

尧雨琴， 李 涛， 胡志华， 高超峰

(上海海事大学 物流研究中心， 上海 201306)



垂岸式集装箱码头自动化跨运车作业任务分派与序列优化

尧雨琴， 李 涛， 胡志华*， 高超峰

(上海海事大学 物流研究中心， 上海 201306)

自动化跨运车(Automated Straddle Carrier，ASC)是一种自动化集装箱码头水平作业设备，可直接在岸桥下从地面存取集装箱，同时在堆场也可直接存取集装箱，其作业不会直接影响岸吊等其他设备的作业效率，具有独立性.考虑垂岸式集装箱堆场布局，以最小化完成时间和空驶时间为目标，建立ASC作业安排的混合整数规划模型，确定ASC的作业序列.根据数值实验结果，分析ASC数量配置的影响，以及完成时间和空驶时间之间的均衡关系.

自动化集装箱码头； 自动化跨运车； 混合整数规划； 调度

自动导引车、自动堆垛起重机和自动化跨越车(Automated straddle carrier，简称ASC)等集装箱码头自动化装卸搬运设备得到广泛应用.随着国际物流对集装箱运输的高要求，各大集装箱码头都在研究和实施自动化集装箱码头建设.ASC不需要与岸桥和堆场起重机的直接协作，即可完成集装箱在岸边和堆场之间的装卸搬运作业.基于ASC的作业工艺和作业系统具有易于实施和控制的特点，在澳大利亚布里斯班等多个集装箱码头推广应用.ASC和自动导引车的调度问题类似，两者都是在自动化码头进行无人操作的运输工具；但是ASC可以自己独立完成集装箱的运输，具有控制简单的灵活性.

在自动化码头的作业过程中，岸桥和堆场起重机等垂直作业设备、自动导向车和ASC等水平作业设备通过协调和调度优化降低设备等待时间、提高码头作业效率.Herry、Cao 等对调度问题建立整数规划模型.Henry[1]考虑设备之间的各种制约因素，研究自动化集装箱码头设备的一体化操作，建立混合整数规划模型.同样，Cao[2]针对集装箱码头在堆场卡车和堆场桥吊的装载作业的调度问题，建立混合整数规划模型.Seyed[3]对自动化码头的运输设备和存储设备建立整数规划模型，使用遗传算法求解.Li[4-5]在考虑堆场起重机在实际操作条件下的问题，建立混合整数规划模型.在Li的基础上，Guo[6]重点研究堆场起重机的服务车队的交付和集卡作业序列.李[7]考虑车辆调度和堆场吊机操作等相关的实际约束，研究卸载集装箱堆场空间分配与车辆调度的集成优化问题，建立整数规划模型.Shahin、Giuseppe等建立整数规划模型后，设计各种启发式算法进行求解.Shahin[8]考虑调度模型的复杂性，基于拉格朗日松弛方法，设计启发式方法求解.Giuseppe[9]将AGV的调度问题转化为最小流问题，建立模型使用贪婪算法和单纯形算法求解，并对比结果.梁[10]将集装箱任务的装卸过程看作岸桥装卸、集卡运输和场桥装卸的三阶段混合Flow Shop调度问题，建立以装卸任务完工时间最小化为目标的混合整数规划模型.Yuan、Cai和Bradley等的研究是本文的基础.针对ASC的调度问题，Yuan[11-12]综合ASC的路径和任务分配问题建立数学模型.Bradley[13]用遗传算法求解模型，更加有效的提高集装箱的装卸效率、ASC使用效率.Cai[14-16]研究基于精确算法的分支定界法和列代法求解自动跨运车的调度问题，建立不确定条件下的ASC调度的多目标规划模型.

本文首先建立ASC在自动化集装箱码头的轨迹的计算方法，然后考虑任务作业时间、任务之间的启动时间(setup time)，在Cai[14]建立的单目标规划模型的基础上，以任务完成时间、空闲时间、空驶时间为优化目标建立多目标混合整数规划模型，确定ASC的作业序列；同时放松最末结束任务，分别以优化空闲时间、空驶时间为目标建立模型，研究均衡关系并优化ASC的作业序列.

1 自动化跨运车

自动化集装箱码头是将集装箱岸边与堆场之间的运输、堆场内的作业、闸口的进出等全过程实现自动化运作的码头.自动化码头包括码头作业区和集装箱存放区，码头作业区的泊位有多个岸吊来负责集装箱的装载和卸载.集装箱堆场则用来临时堆放集装箱，集装箱的每个区有一个吊机负责本区集装箱的相关移动.卡车服务于堆场吊车和码头岸吊进行运输.

图1为一个基于自动化跨运车的自动化集装箱码头平面图.为了便于路径的计算，考虑纵横两个方向建立坐标系.图中有六座岸桥，每个岸桥下都有1个集装箱临时堆存区、3个堆场、60个垂岸箱区，3个闭环的ASC运行轨道(通过地下磁场或GPS等技术导航).在集装箱卸船作业中，船舶首先停靠在码头为其分配的泊位处，需要卸载的集装箱由岸吊拾取至临时堆存区，再由ASC从地面拾取后运输到堆场；卸载至堆场的存放位置.集装箱装船作业的顺序与卸船作业相反.ASC的运行轨迹跟作业有关，根据集装箱拾取的位置和放置的位置确定其路径.

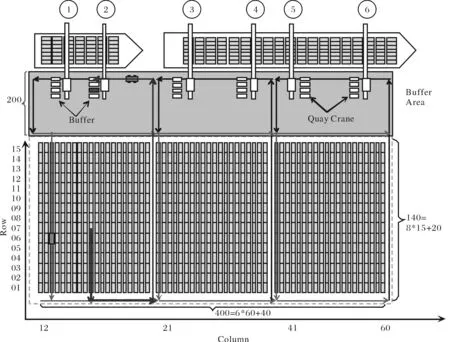
图1 一个基于ASC的垂岸式自动化集装箱码头Fig.1 A shore-based ASC vertical container terminal automation

2 装卸作业任务的带箱和空驶时间计算

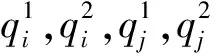
算法1 装卸作业任务的带箱行驶时间

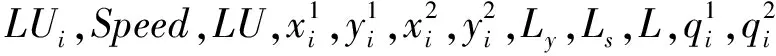
输出 Di，Ti

步骤

步骤1:根据LUi，计算距离Di，如果LUi=1，则步骤(2)，否则步骤(3).

步骤2:根据作业任务在岸边的相对位置计算行驶时间.

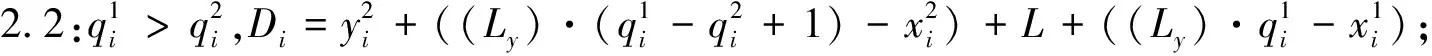
步骤3:根据作业任务在堆场的相对位置计算行驶时间.

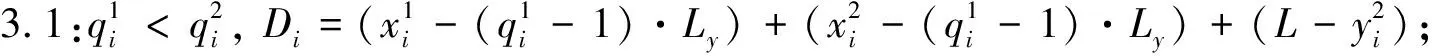
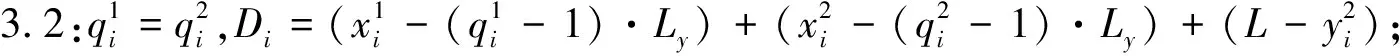
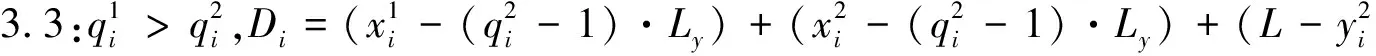
步骤4:根据距离Di，计算时间Ti=Di/Speed.

算法2 装卸作业任务之间的启动时间

输出 Dij，Tij

步骤

步骤1:根据LUi，LUj，i∈I，j∈I的值，计算距离Dij，计算完成后根据步骤(6)计算.

如果LUi=LUj=1，转步骤(2)；

如果LUi=LUj=0，转步骤(3)；

如果LUi=1，LUj=0，转步骤(4)；

如果LUi=0，LUj=1，转步骤(5).

步骤2:根据相邻作业任务在岸边和堆场相对位置计算行驶时间.

当碰撞为完全弹性时，碰撞后,二者的速度是不同的，如果碰撞后铅层的速度用v′表示，则根据过程中动量和能量守恒,得到

步骤3:根据相邻作业任务在岸边和堆场的相对位置计算行驶时间.

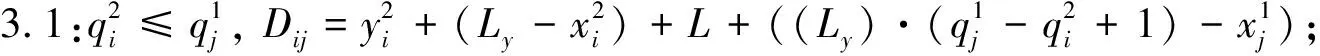
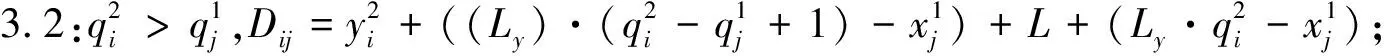
步骤4:根据相邻作业任务在岸边的相对位置计算行驶时间.

步骤5:根据相邻作业任务在堆场的相对位置计算行驶时间.

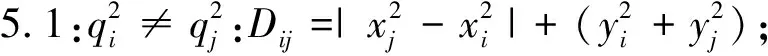
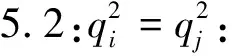
步骤6:根据距离Dij，计算时间Tij=Dij/Speed.

3 模型

3.1 符号

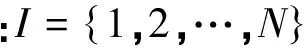
3.2 基本模型

自动化集装箱码头ASC的调度问题，以最小化最末任务结束时间为目标建立单目标模型[M1]，模型的目标函数与约束条件如下.

[M1] min fMakespan,

(1)

s.t. fMakespan≥zi+Ti，∀i∈I,

(2)

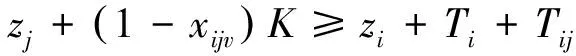
∀i≠j，v∈V,

(3)

zi≥Ai，∀i∈I,

(4)

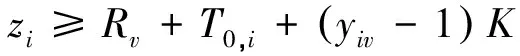
∀i∈I，v∈V,

(5)

∑j∈I+{i} xjiv=∑j∈I+{i} xijv=yiv，

∀i∈I，v∈V,

(6)

∑vyiv=1，∀i∈I,

(7)

xijv+xjiv≤1，∀i，j∈I，i≠j，v∈V,

(8)

∑i∈I+{0} x0，i，v=1，∀v∈V,

(9)

∑i∈I+{N+1} xi，N+1，v=1，∀v∈V,

(10)

fMakespan≥0，zi≥0，∀i∈I.

(11)

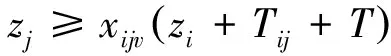
3.3 多目标模型

基于基本模型[M1]建立模型[M2]，得到最末任务结束时间；基于基本模型[M1]建立多目标模型[M3]； ASC的空闲时间的计算如式(14)；ASC等待任务时间的计算如式(15)所示；[M4]和[M5]是在放松最末任务结束时间时，fIdle，fEmpty的值的变化.

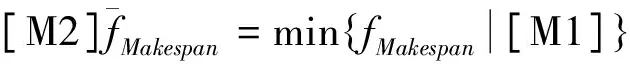
(12)

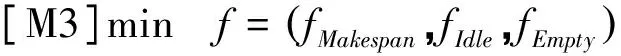
(13)

s.t. Eqs.(1-10),

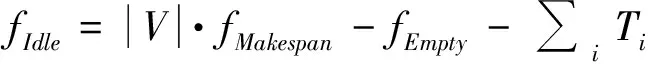
(14)

fEmpty=∑v，i∈I+，j∈I+xijvTij,

(15)

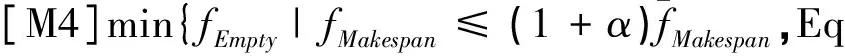
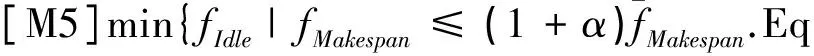
4 算例

4.1 实验设计

本文算例中根据表1做4个实验，对模型进行求解分析，如表1所示.表2是15个集装箱运输作业的基本信息.

表1 实验场景

表2 任务数据集

续表2

4.2 实验结果

本文用MATLAB中的YALMIP工具箱结合GUROBI6.0求解器对建立的模型进行求解.

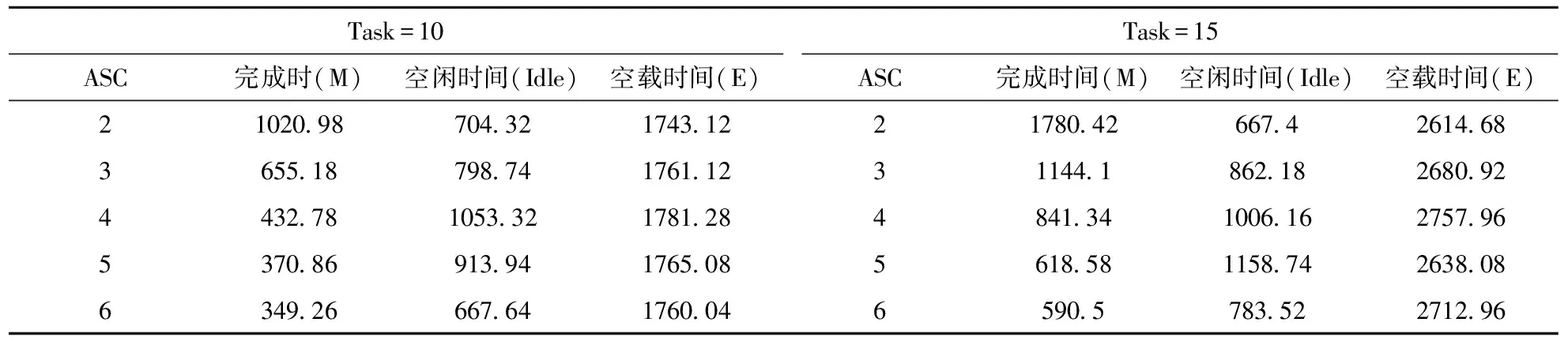
表3 模型[M3]的结果

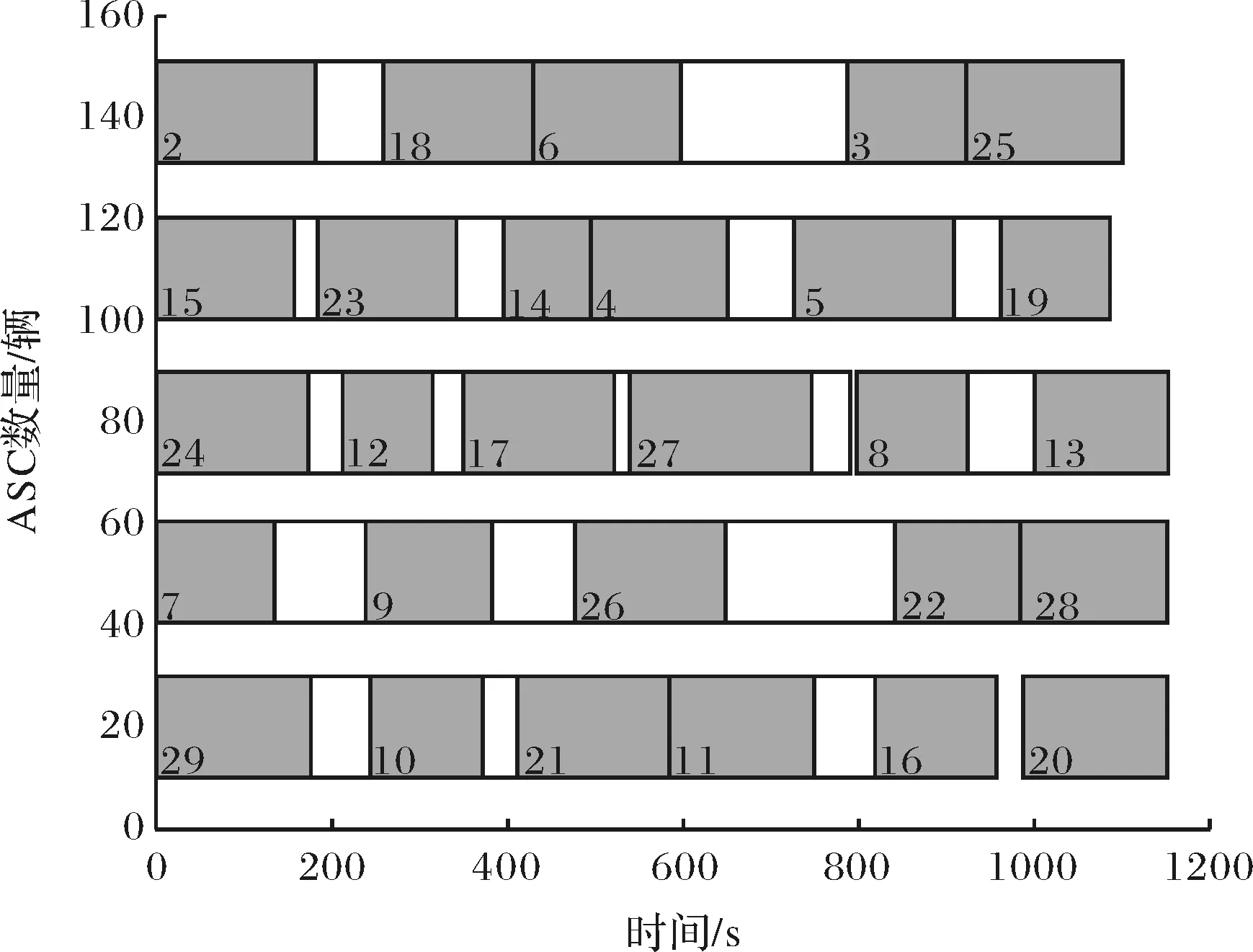
图2 求解[M4]所得的ASC作业序列Fig.2 ASC’s sequence of model [M4]

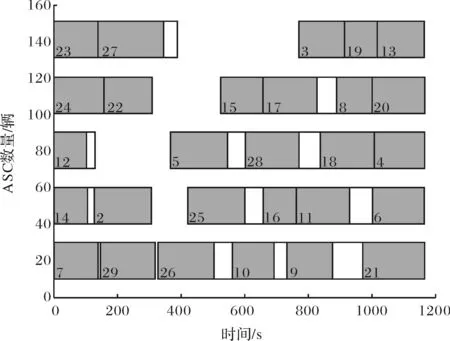
图3 求解[M5]所得的ASC作业序列Fig.3 ASC’s sequence of model [M5]

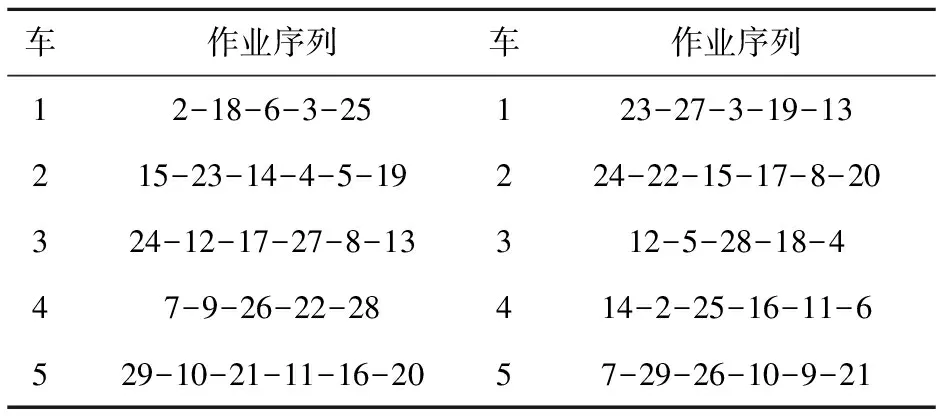
车作业序列车作业序列12-18-6-3-25123-27-3-19-13215-23-14-4-5-19224-22-15-17-8-20324-12-17-27-8-13312-5-28-18-447-9-26-22-28414-2-25-16-11-6529-10-21-11-16-2057-29-26-10-9-21

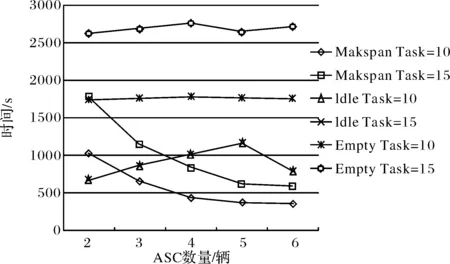
图4 实验一得到的结果Fig.4 Result of first experiment

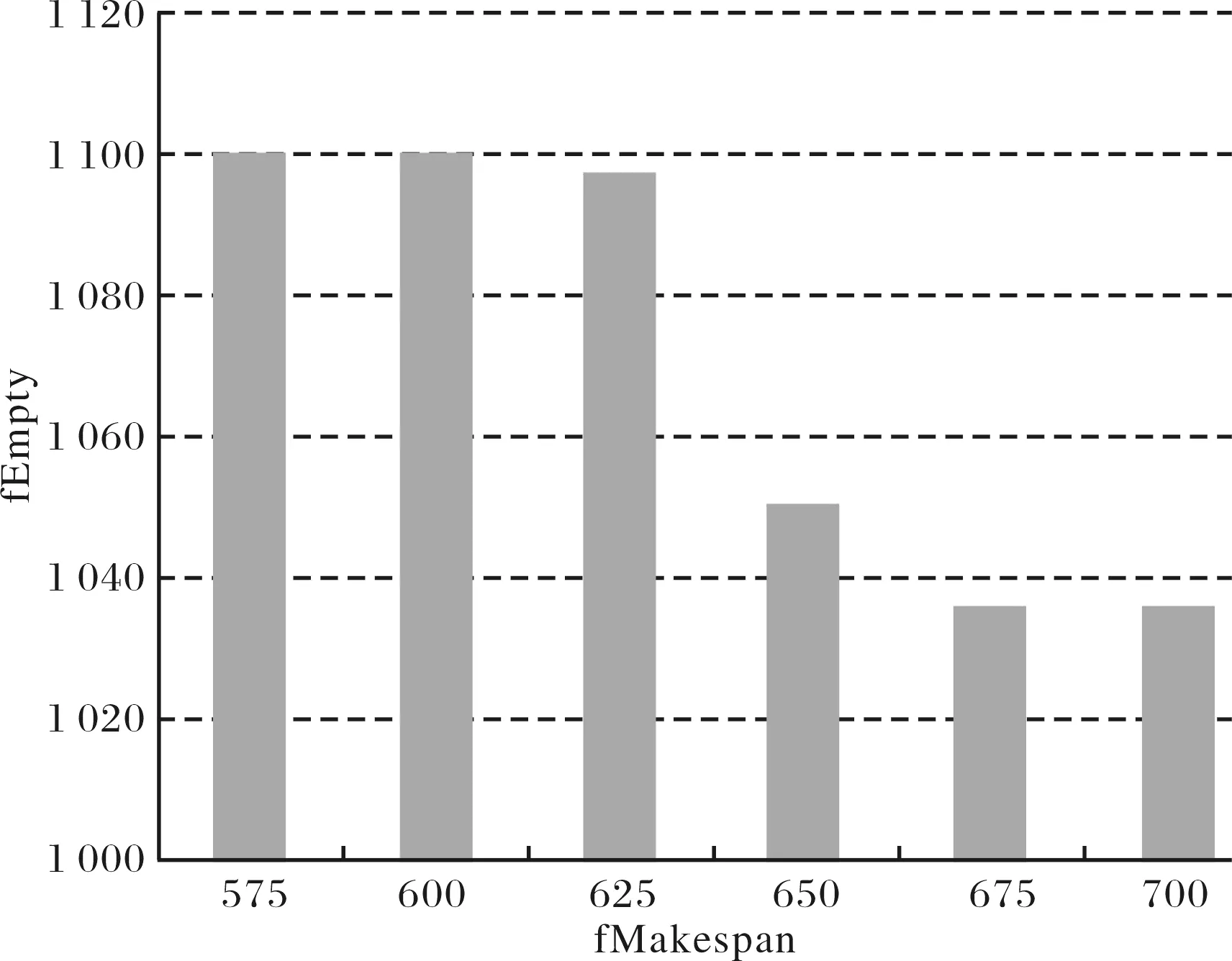
图5 最末任务结束时间变化对[M5]的影响Fig.5 The affection of the final times on [M5]

1) 在实验1中，对模型[M1]、[M2]、[M3]进行求解，得到的结果如表3所示，即在不同ASC和不同任务下最末任务结束时间、ASC等待任务时间、ASC的空闲时间.图4对表3的结果进行画图分析，根据图4可以得出结论：ASC数量、任务的变化对ASC的空闲时间没有影响；任务数量一定时，ASC数量增加，最末任务结束时间会减少，相反ASC等待任务时间会增加；当ASC数量达到一定值后，最末任务结束时间几乎没有变化，ASC等待任务时间呈减少趋势.

2)在实验2中，对[M4]、[M5]两个多目标模型进行求解，改变∂值，得到图2、图3结果，并且得到ASC的作业任务序列，如表4所示.

3) 改变多目标模型中[M4]的α值，得到在不同α下模型的结果，两者呈现一个线性关系，随着最末任务结束时间减少，ASC等待任务时间的等待时间也在减少.

4) 改变多目标模型中[M5]的α值，得到在不同α下模型的结果，得到图5，图5可以看出，随着最末任务结束时间的增大呈减少趋势，但是最末任务结束时间对ASC的空闲时间呈非线性关系，并且ASC的空闲时间只在一定的区间范围内受影响，超过区间值，ASC的空闲时间变化很小.

根据以上4种实验，可以知道作业任务和ASC数量对设备利用率有很大的影响，随着作业任务和ASC数量的改变，ASC车子的利用率有很大的影响；根据实验3和实验4可知，最末任务结束时间对ASC等待任务时间的影响比对ASC的空闲时间影响更大，ASC等待任务时间的敏感性更高.对ASC作业序列进行优化主要考虑ASC等待任务时间.

5 结论

本文研究自动化集装箱码头的ASC调度问题，以最小化最末任务结束时间为目标、最小化ASC等待任务时间、最小化ASC的空闲时间为目标，建立多目标混合整数规划模型.然后，通过转化成为可计算的单目标模型研究作业任务和ASC数量对设备利用率的影响，并分析完成时间和空驶时间之间的关系，优化ASC的作业序列.在自动化集装箱码头中，通常存在多种运输设备，合理安排不同设备的作业任务序列并改进不同作业设备之间的协调机制，是影响码头作业效率的重要因素.

[1] LAU H Y K , ZHAO Y. Integrated scheduling of handling equipment at automated container terminals[J]. International Journal of Production Economics, 2008, 112(2): 665-682．

[2] CAO J X, LEE D-H, CHEN J H, et al. The integrated yard truck and yard crane scheduling problem: Benders’ decomposition-based methods[J]. Transportation Research Part E: Logistics and Transportation Review, 2010, 46(3): 344-353．

[3] HOMAYOUIN S M, TANG S H, MOTLAGH O. A genetic algorithm for optimization of integrated scheduling of cranes, vehicles, and storage platforms at automated container terminals[J]. Journal of Computational and Applied Mathematics, 2014, 270(42): 545-556．

[4] LI W, WU Y, PETERING M E H, et al. Discrete time model and algorithms for container yard crane scheduling[J]. European Journal of Operational Research, 2009, 198(1): 165-172．

[5] LI W, GOH M, WU Y, et al. A continuous time model for multiple yard crane scheduling with last minute job arrivals[J]. International Journal of Production Economics, 2012, 136(2): 332-343．

[6] GUO X, HUANG S Y, HSU W J, et al. Dynamic yard crane dispatching in container terminals with predicted vehicle arrival information[J]. Advanced Engineering Informatics, 2011, 25(3): 472-484．

[7] 李 坤, 唐立树, 陈树发. 多集装箱堆场空间分配与车辆调度集成问题的建模与优化[J]. 系统工程理论与实践, 2014, 34(1): 115-121．

[8] GELAREH S, MERZOUKI R, MCGINLEY K, et al. Scheduling of Intelligent and autonomous vehicles under pairing/unpairing collaboration strategy in container terminals[J]. Transportation Research Part C: Emerging Technologies, 2013, 33: 1-21．

[9] CONFESSORE G, FABIANO M, LIOTTA G. A network flow based heuristic approach for optimising AGV movements[J]. Journal of Intelligent Manufacturing, 2011, 24(2): 405-419．

[10] 梁承姬, 张松波. 集装箱港口装卸作业设备集成调度[J]. 辽宁工程技术大学学报(自然科学版),2015, 34(2): 262-266．

[11] YUAN S, SKINNER B T, HUANG S D, et al. Mathematical modelling of container transfers for a fleet of autonomous straddle carriers. [J]. IEEE international conference on robotics and automation, 2010(10): 1261-1266．

[12] YUAN S, SKINNER B T, HUANG S, et al. A job grouping approach for planning container transfers at automated seaport container terminals[J]. Advanced Engineering Informatics, 2011, 25(3): 413-426．

[13] SKINNER B, YUAN S, HUANG S, et al. Optimisation for job scheduling at automated container terminals using genetic algorithm[J]. Computers & Industrial Engineering, 2013, 64(1): 511-523．

[14] CAI B, HUANG S, LIU D, et al. Optimisation model and exact algorithm for autonomous straddle carrier scheduling at automated container terminals[J]. Advanced Engineering Informatics, 2011, 10(1016): 3687-3693．

[15] CAI B, HUANG S, LIU D, et al. Multiobjective optimization for autonomous straddle carrier scheduling at automated container terminals[J]. Transactions on Automation Science and Engineering, 2013, 10(3): 711-724．

[16] CAI B, HUANG S, LIU D, et al. Rescheduling policies for large-scale task allocation of autonomous straddle carriers under uncertainty at automated container terminals[J]. Robotics and Autonomous Systems, 2014, 62(4): 506-514．

Scheduling automated straddle carrier at automated container terminals

YAO Yuqin， LI Tao， HU Zhihua， GAO Chaofeng

(Logistics Research Center， Shanghai Maritime University， Shanghai 201306)

Automated straddle carriers(ASC)is an automated horizontal operating equipment for container terminal， which independently allows direct access to containers both under the shore bridge and the yard without directly affecting the operating efficiency of quay cranes and other equipment. The present study focuses on minimizing the completion and idle time considering the vertical layout of the container yard. The mixed-integer linear program model is established to arrange the ASC operation and determine its sequence. According to the results of numerical experiments， the impact of quantity allocation of ASC is analyzed along with the equilibrium relation between the completion time and idle time．

automated container terminal； automated straddle carrier； mixed-integer linear program； scheduling

2015-06-30.

国家自然科学基金青年项目(71101088)；国家自然科学基金面上项目(71471109)；上海市曙光计划项目(13SG48)；交通部应用基础研究项目(2015329810260)．

1000-1190(2016)01-0067-07

C93

A

*通讯联系人. E-mail: 865502147@qq.com.