基于改进PSO的ICA方法分析重力固体潮信号

李巧燕， 全海燕

(昆明理工大学 信息工程与自动化学院， 昆明 650500)



基于改进PSO的ICA方法分析重力固体潮信号

李巧燕， 全海燕*

(昆明理工大学 信息工程与自动化学院， 昆明 650500)

为了从重力固体潮信号中提取地球物理信息，介绍了一种重力固体潮信号分解模型.在分解模型中，重力固体潮信号分解为赤道平面信号分量及地球自转轴信号分量.为了提取与分解模型相一致的地球物理信息，提出用独立分量分析(ICA)方法将重力固体潮信号中的赤道平面信号分量与地球自转轴信号分量分离.鉴于ICA存在收敛速度慢及局部搜索等特点，提出了一种基于惯性因子ω的改进粒子群优化算法(PSO)来解决ICA中的全局寻优问题.通过仿真实验分析可知，本文提出的改进粒子群的独立分量分析算法可以获得与分解模型相一致的信号分量，并且从各分量中可提取出与地球产生机制相一致的地球物理信息，是一种分析重力固体潮信号的有效方法.

地球物理信息； 重力固体潮信号； 独立分量分析(ICA)； 粒子群优化算法(PSO)

地球受到太阳、月亮的引潮力影响使得地球整体产生周期性变化.地球的这种整体周期性形变称为固体潮[1].重力固体潮即是引潮力引起的沿地心方向重力值的周期性变化.重力固体潮信号不但反映了重要的地球物理信息，而且可能反映出地震的前兆信息.因此，提取重力固体潮信号中的地球物理信息是研究重力固体潮信号的重要内容.

由于地球与其它星球的距离比较远，所以我们一般研究的是地球受到太阳及月亮的引潮力作用.作用于地球上不同点处的引潮力引起的固体潮可以分解为地倾斜固体潮信号分量及重力固体潮信号分量.本文主要分析重力固体潮信号.重力固体潮信号中的物理信息主要包括日波、半日波，月波、半月波，年波、半年波.地球自转轨道的周期性变化体现在重力固体潮信号上为日波、半日波.地球绕太阳公转轨道的周期性变化体现在重力固体潮信号上形成年波、半年波.月亮绕地球旋转轨道的周期性变化体现在重力固体潮信号上形成月波、半月波.

为了有效提取出重力固体潮信号中含有的以上地球物理信息，并揭示它们之间的调制关系，本文提出一种重力固体潮信号分解模型.基于这种分解模型将重力固体潮信号分解为平行赤道平面信号分量及地球自转轴信号分量.本文提出一种改进PSO的ICA算法来分离重力固体潮信号，以获得与分解模型一致的信号分量.通过这种分离方法，有效地将重力固体潮信号中的赤道平面信号分量及地球自转轴信号分量分离，并得到了这些分量中所含的地球物理信息.

1 重力固体潮信号的一种分解模型

如图1所示，A为地球上某观测点，先考虑 A点受到太阳作用的引潮力.设该引潮力引起的固体潮为F，该固体潮可分解为地倾斜固体潮Fh及重力固体潮Fg.

对于重力固体潮Fg，又可将其分解为两个分量:一个为平行于地球自转轴方向的分量F1(称为地球自转轴分量)，另一个为平行于赤道平面的分量F2(称为赤道平面分量).显然，F1与地球自转无关，所以，F1分量体现在重力固体潮信号中主要为年波、半年波等成分，不含日波、半日波成分.而 F2不但与地球自转相关，而且与地球绕太阳公转有关，所以F2分量体现在重力固体潮信号中不但含有日波、半日波成分，而且含有年波、半年波等成分，这些成分之间的关系可通过对F2分量的分析得到.

地球上的观测点同时也受到月亮的引潮力作用，所以，A点受到月亮作用的引潮力引起的固体潮分解模型也与上面太阳作用的引潮力引起的固体潮分解模型相似.

基于上面提出的重力固体潮信号分解模型，可有效分解出地球自转导致的日波、半日波成分，月亮绕地球旋转产生的月波、半月波成分，地球绕太阳公转产生的年波、半年波成分.

为了提取重力固体潮信号中的地球物理信息，本文用独立分量分析方法(ICA)对重力固体潮信号进行独立成分分析，得到了与上面重力固体潮信号分解模型一致的结果.其中，不但得到了日波、半日波、月波等成分，而且揭示了他们之间的调制关系.

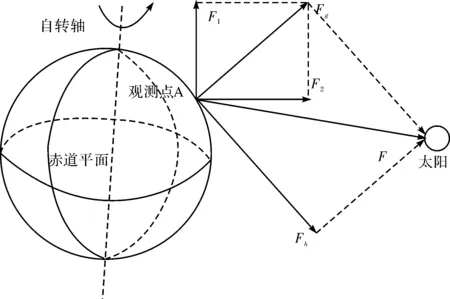
图1 重力固体潮信号分解模型图Fig.1 The decomposed model of gravity earth tide

2 基于改进PSO的ICA算法

2.1 独立分量分析算法

由于作用于地球任意点上的重力固体潮信号是赤道平面信号分量及地球自转轴信号分量的混合信号，所以本文采用独立分量分析的方法将重力固体潮信号分解，使重力固体潮信号中各分量之间相互独立.

独立分量分析(ICA)是20世纪90年代发展起来的信号分量技术[2]，属于盲信号分离方法之一.该算法是混合信号(多个独立信号形成)经过去均值、白化/球化运算，再与解混矩阵进行运算，得到解混输出信号的过程[3].因为ICA算法可以准确地对混合信号进行分离，使得ICA算法在混合图像分离、语音信号分离、生物医学信号处理等方面起着重要作用.

原信号S(t)由N维信号组成,且信号s1(t)，…，sN(t)之间相互统计独立.当原信号S(t)经混合矩阵AM×N运算之后，得混合信号X(t)=AS(t).一般我们取M=N，则X(t)=[x1(t)，…，xN(t)]T.对混合信号X(t)按(1)式进行去均值，得去均值信号C(t).C(t)经式(2)白化处理之后得到白化信号Z(t)，Z(t)通过式(3)可获得解混输出信号y(t).

C(t)=X(t)-E(X(t)),

(1)

Z(t)=WC(t),

(2)

y(t)=BZ(t),

(3)

式中，B为解混矩阵，解混输出信号y(t)为原信号S(t)的估计.

按照目标函数的不同和求解解混矩阵B的算法不同，可以构成各种ICA算法[4].一般的ICA算法具有依赖梯度信息、局部搜索及收敛速度慢等特点[5]，鉴于PSO具有全局搜寻及快速收敛的优点，本文提出了一种基于惯性因子来改进粒子群优化算法(PSO)，通过改进后的PSO算法来优化ICA中的解混矩阵B.

2.2 改进PSO算法

粒子群算法是一种通过模拟鸟类的飞翔觅食行为而建立起来的智能优化算法，简称是PSO[6].Eberhart等最先提出了基本PSO算法.在算法中每一个独立的个体叫做“粒子”，每个粒子相当于一个目标函数的解.多个粒子组成的群体叫“种群”.PSO算法是通过粒子之间的“自身学习”和粒子之间的“相互学习”来寻找种群中的最优粒子.粒子的“学习”实际上就是粒子不断地向最优粒子趋近的过程，这个过程是通过适应函数取值的不断增加或减小来确定的.算法中适应函数的选择则依据具体的问题来确定.本文所用的适应函数则是ICA中的目标函数.由于基本PSO算法开发能力太差，后来学者们在PSO算法中加入惯性因子ω来调节算法的全局和局部寻优能力.加入惯性因子ω后的标准PSO算法如下.

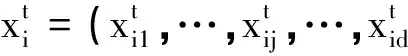
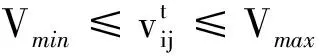
(4)

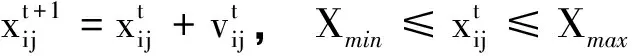
(5)

由于ω取值策略对于粒子寻优具有重要的影响，Shi等人提出了惯性因子ω从0.9线性递减到0.4的改进算法[7].虽然这种改进算法可以保证算法初期对粒子进行全局寻优和算法后期对粒子进行局部寻优，但是由于算法后期的惯性权重值比较低，使得算法容易陷入局部最优，难以找到最优粒子.

为了解决PSO容易陷入局部最优的问题，本文提出了一种针对ω的分段随机化选取方法.通过不断地实验验证，本文将[0.4，0.9]分为[0.4，0.7)及[0.7，0.9]两段.在求ω时，随机的从两个分段区间中任意选择一个区间，然后从所选的区间内随机取值赋值给ω.ω的改进策略公式为：

(6)

本文提出的改进算法是通过自由选取ω的值，增加粒子的惯性因子随机选择的可能性，从而使ω具有一定的自适应能力.同时，改进算法在算法初期及后期均可以获得较大的惯性权重，这既确保了初期的全局搜索能力，又可使粒子在后期跳出局部最优，继续搜寻最优粒子.

3 基于改进PSO的ICA算法

改进后的PSO算法与基本PSO算法相比，不但具有更高的收敛速度，而且避免了传统PSO算法容易陷入局部最优的缺点.这就使得改进PSO与ICA结合时，ICA可以全局寻优并可提高ICA的收敛速度.所以，本文提出了一种利用改进PSO算法来优化ICA中解混矩阵B的方法.

ICA中适应度函数选取类型有多种，本文采用互信息量作为PSO算法的优化函数.对于y(t)=BX(t)的线性运算，输入与输出的互信息量关系可以表示为[8]：

I(y)= H(x)-log|B|+

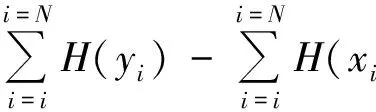
(7)

由于x为已知的，所以可以将(7)变为

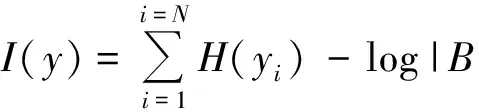
(8)

若式(8)中I(y)=0，则表示y中的各分量相互独立.对于式(8)中的H(y)我们则采用的Gram-Charlier展开式来逼近[9].

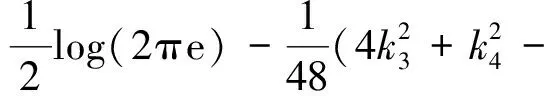
(9)

基于以上的算法原理，改进PSO的ICA算法步骤如下：

1) 利用式(1)对混合信号X(t)进行去均值，得到去均值后的信号C(t).

2) 利用式(2)对C(t)进行白化处理，得白化后的观测信号Z(t).

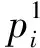
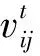
4 实验结果分析

根据本文第2节中提出的重力固体潮信号分解模型，为了提取重力固体潮信号中的地球物理信息，分别选取纬度为(10°N，0°，10°S)、(30°N，0°，30°S)、(50°N，0°，50°S)经度均为0°的3组重力固体潮信号进行ICA分析.算法处理流程如图2所示.3组重力固体潮信号经过PCA(主成分分析)预处理之后，得到PCA去相关后信号x1(t)、x2(t)、x3(t)，其信号仿真图如图3所示.由于PCA去相关只是对信号进行到二阶运算，所以去相关后信号x1(t)、x2(t)、x3(t)仍为混合信号.将X(t)=[x1(t);x2(t);x3(t)]作为改进PSO的ICA的输入信号，对混合信号X(t)进行分离，得重力固体潮解混输出信号Y(t).重力固体潮解混输出信号Y(t)的仿真图，如图4所示.由图4可知，解混输出信号Y(t)分离成y1(t)、y2(t)、y3(t)三路信号.对于本实验，种群大小M=30；因为输入信号个数为3，所以D=9；循环次数Num=300.

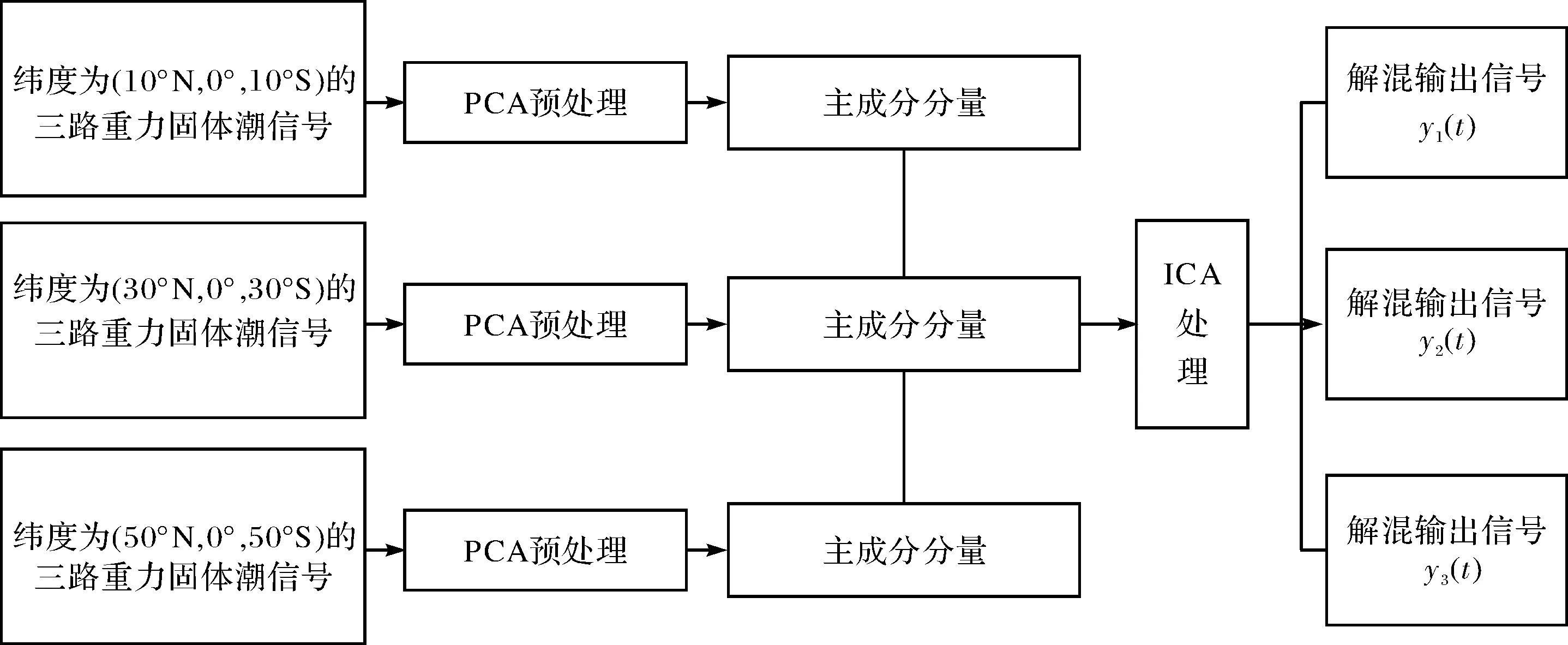
图2 重力固体潮信号处理流程图Fig.2 Process flow chart of gravity earth tide

图3 PCA去相关后主成分信号Fig.3 Principle signals after PCA

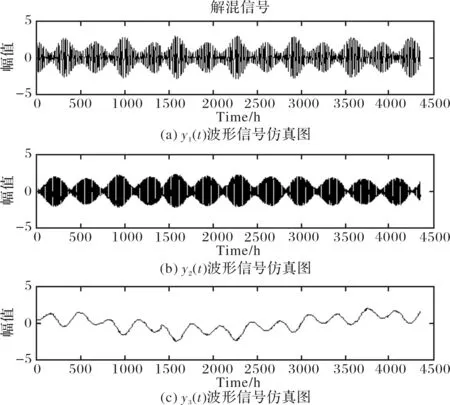
图4 ICA解混后信号Fig.4 Signals after ICA

波形年波半年波月波半月波日波半日波频率/HZ3．210×10-86．430×10-83．8580×10-77．7160×10-71．1570×10-52．3148×10-5

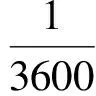
为了进一步得到重力固体潮解混输出信号Y(t)中各分量的地球物理信息的参数值，本文对Y(t)进行频谱分析.解混信号Y(t)频谱分析如图5所示.解混信号Y(t)中各分量中所含的频率成分如表2所示.

解混信号y1(t)的频谱分析结果如图5(a)所示.由图5(a)可知：y1(t)的载波信号的频率是1.119×10-5Hz，调制波信号频率8.65×10-7Hz.由表1可知：在允许的误差范围内，y1(t)是载波信号为日波，调制信号为半月波的信号.解混信号y2(t)的频谱分析结果如图5(b)所示.由图5(b)可知：y2(t)载波信号的频率2.2760×10-5Hz，调制波信号频率是3.8×10-7Hz.由表1可知,在允许的误差范围内， y2(t)为载波信号为半日波，调制信号为月波的信号.通过对解混信号y3(t)的频谱分析如图5(c)所示.由图5(c)可知：f1=6.393×10-8Hz、f2=4.475×10-7Hz、f3=8.311×10-7Hz由表1可知,信号y3(t)是含有频率成分为半年波、月波及半月波的信号.

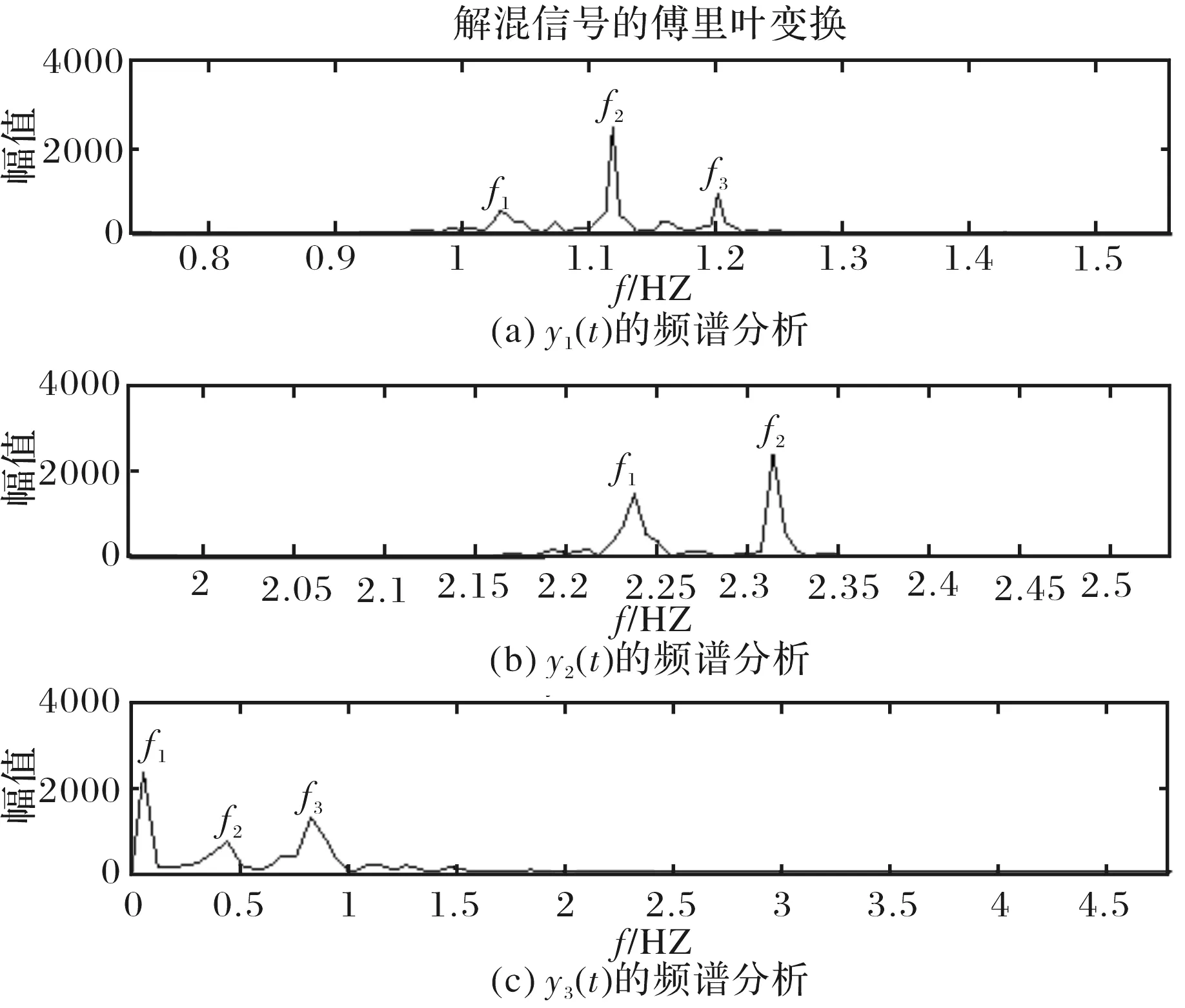
图5 解混输出信号的频谱分析图Fig.5 Spectrum analysis diagrams of output signals

图形图(a)图(b)图(c)频率/Hzf1f2f3f1f2f1f2f31．029×10-51．119×10-51．202×10-52．238×10-52．314×10-56．393×10-84．475×10-78．311×10-7

通过对解混输出信号进行频谱分析可知，重力固体潮信号经过PCA预处理及本文提出的改进PSO及ICA算法可分解为平行赤道平面信号分量及地球自转轴信号分量.赤道平面信号分量体现在实验结果中为解混信号y1(t)及解混信号y2(t)，地球自转轴信号分量体现在实验结果中为y3(t).由仿真实验实验结果可知：平行赤道平面信号分量中主要含有日波、半日波及月波、半月波及半年波的调制成分.地球自转轴信号分量主要含有半年波、月波及半月波等物理信息.仿真实验结果与本文重力固体潮信号分解模型中提出的地球自转轴信号分量因与地球自转无关，而不含有日波、半日波成分；赤道平面信号因受地球及月亮的作用，日波、半日波中含有月波、半月波等调制成分理论分析相一致.

5 结论

本文提出一个重力固体潮信号的分析模型，该模型将重力固体潮信号正交分解为赤道平面信号分量及地球自转轴信号分量.同时，基于改进的PSO优化算法通过独立分量分析将正交独立的赤道平面信号分量与地球自转轴信号分量分离，并从赤道平面信号分量中提取出日波、半日波等物理信息，从地球自转轴信号分量提取出月波、半月波及半年波等地球物理信息.通过重力固体潮信号实验分析可以充分说明：

1)独立分量分析方法能有效地分离出重力固体潮信号中的正交独立分量.

2) 从分解出的正交独立分量能提取出与重力固体潮信号产生机制一致的地球物理信息.

3)将重力固体潮信号正交分解为赤道平面信号分量及地球自转轴信号分量是一个分析重力固体潮信号的有效模型.基于该模型，能提取重力固体潮信号中与产生机制一致的地球物理信息.

研究中也发现：从重力固体潮信号中提取出的反映地球物理信息的各个分量中，存在乘性的调制关系.所以，需要进一步研究各个分量中具体的乘性调制关系.

[1] 李瑞浩. 重力学引论[M]. 北京：科学出版社，1988．

[2] 张银雪， 王学民. 基于改进PSO-ICA的地震信号去噪方法[J]. 石油地球物理勘探. 2012, 47(1): 56-62.

[3] 周书仁， 梁昔明， 杨秋芬， 等. 基于改进PSO与ICA的表情特征提取[J]. 计算机应用. 2007, 27(11): 2797-2803.

[4] 孙路路. 基于ICA的混合图像盲分离算法研究[D]. 南京: 南京邮电大学， 2010:18-19.

[5] 李刚磊. 基于改进粒子群的ICA算法[J]. 科技信息. 2011, 26:81-82.

[6] 谭 萍， 李伟娟， 李 明. 基于改进粒子群算法的独立分量分析[J]. 兰州大学学报: 自然科学版， 2010, 46(4)：124-128.

[7] 李 丽， 牛 奔. 粒子群优化算法[M]. 北京：冶金工业出版社，2009．

[8] 杨福生， 洪 波. 独立分量分析的原理与应用[M]. 北京：清华大学出版社，2006.

[9]REJUVG，KOHSN，YANNSI.Partialseparationmethodforsolvingpermutetionprobleminfrequencydomainblindsourceseparationofspeechsignals[J].Neurocomputing，2008， 71(10/12):2098-2112．

Analyze gravity earth tide based on the method of improved PSO and ICA

LI Qiaoyan， QUAN Haiyan

(Institute of Information Engineering and Automation，Kunming University of Science and Technology， Kunming 650500)

In order to extract the geophysical information from the gravity earth tide, a model for signal decomposition is introduced in the present work. In this model, the signal of tidal gravity is divided into two parts. One signal is in parallel with the equatorial plane. The other is in parallel with the axis of earth rotation. Independent Component Analysis (ICA) is applied to separate the tidal gravity signal and get the geophysical information according to the decomposed model. Because of the slowly convergence speed and local search for the target, improved particle swarm optimization algorithm (PSO) is used to search the optical target globally. Results from simulation experiments show tidal gravity signals divided from this method are consistent with the geophysical information.

geophysical information; gravity earth tide; independent component analysis (ICA); particle swarm optimization algorithm (PSO)

2015-06-08.

国家自然科学基金项目(41364002)；云南省自然科学基金项目(2009ZC048M)；昆明理工大学校人才培养基金项目(KKZ3201103022)．

1000-1190(2016)01-0049-06

P223

A

*通讯联系人. E-mail: quanhaiyan@163.com.