固体潮模型在GPS/BDS PPP 中的影响分析
梁杰华,常 列,宋春龙
(1.交通运输部南海航海保障中心 广州海事测绘中心,广东 广州 510000;2.山东正元数字城市建设有限公司,山东 烟台 264000)
地球固体潮是指固体地球在日月引力作用下引起的弹性形变,使地球表面产生周期性的涨落[1-2]。研究表明,固体潮会使测站的位置坐标产生周期性变化,垂直方向最大位移为80 cm。在精密单点定位(PPP)过程中,若进行长时间静态观测,一般可消除大部分周期项误差,但无法完全消除长期项误差,通常采用模型进行改正[3]。固体潮与海潮形成的原因相同,但模型的建立远比海潮模型复杂[4]。随着全球导航卫星系统(GNSS)的快速发展,北斗卫星导航系统(BDS)正式组网,将在导航、定位和授时等方面提供服务[5]。PPP 技术因具备无需基准站、不受距离限制、高精度和低成本的优点,受到GNSS 用户青睐和支持[6-8]。如何进一步提高PPP 精度是广大学者面临的问题,而固体潮模型改正是进一步提高PPP 定位精度的方式之一,也是国内外学者的研究方向之一。李艳红[3]等分析了全球范围内66 个IGS 站BDS 观测数据的固体潮影响,结果表明固体潮对U 方向改正量最大,部分测站改正量大于10 cm,且在BDS PPP 过程中必须加入固体潮改正;胡金林[9]基于IERS2003 固体潮模型对5 个IGS 站和两个CORS站GPS 观测数据进行解算,结果表明固体潮模型对测站N、E 和U 方向均有较明显的改正,基于IERS2003 固体潮模型的改正可达毫米级定位精度;肖亮明[10]等对全球33 个IGS 观测站数据进行研究发现,固体潮模型在GPS PPP定位中改正量可达10 cm,且存在周期性变化规律。已有文献主要分析固体潮改正模型在GPS或BDS数据静态PPP的改正量,缺少固体潮改正模型对GPS、BDS-2、BDS-3、BDS-2+BDS-3 和GPS+BDS-2+BDS-3 PPP 改正量综合性分析的文献。因此,本文基于IGS 分析中心提供的GPS 和BDS 观测数据,对比分析了固体潮改正模型在GPS、BDS-2、BDS-3、BDS-2+BDS-3和GPS+BDS-2+BDS-3 PPP中的影响。
1 数学模型
1.1 固体潮改正模型
固体潮改正通常只考虑二阶潮和三阶潮的影响。二阶潮、三阶潮改正的表达式分别为[9]:
式中,GMj为万有引力常数,j=2 为月亮、j=3 为太阳;GMi为地球万有引力常数;R̂j、Rj分别为地心到月球/太阳距离的单位向量和模;Re为地球赤道半径;r̂、r分别为地心到测站距离的单位向量和模;h2为2阶Love数的标称值;l2为2阶Shida数的标称值。
1.2 双频无电离层PPP
双频PPP定位模型的表达式为[11-12]:
式中,PIF、ϑIF分别为伪距观测值和相位观测值,单位为m;f1、f2分别为载波相位观测值的频率,单位为MHz。
2 数据选取与处理策略
为对比分析固体潮改正模型在GPS、BDS-2、BDS-3、BDS-2+BDS-3 和GPS+BDS-2+BDS-3 PPP 中的应用,本文选取2020 年年积日001—060 全球具有GPS 和BDS 观测数据的20 个IGS 站观测数据进行处理,站点分布见图1。
图1 站点分布图
本文设计了5 组对照实验(10 个方案),各方案的电离层延迟均采用无电离层组合模型,对流层延迟均采用Saastamoinen模型+GMF映射函数进行改正,精密星历均采用事后SP3 产品,天线相位中心均使用IGS14 产品进行改正。第一组实验采用GPS 观测数据,方案1 未使用固体潮模型改正,方案2 采用IERS2003固体潮模型进行改正,通过对比二者的静态PPP,可进一步研究固体潮模型对GPS PPP 的影响;同理,第二、三、四、五组实验分别对比分析固体潮模型在BDS-2、BDS-3、BDS-2+BDS-3、GPS+BDS-2+BDS-3中的影响。
3 实验结果分析
本文以IGS 数据中心提供的测站坐标为参考值,将未进行固体潮改正和固体潮改正的静态PPP结果分别与参考值求差,以两组差值的互差绝对值表示固体潮改正模型对PPP 的影响。GPS、BDS-2、BDS-3、BDS-2+BDS-3、GPS+BDS-2+BDS-3 静态PPP 在N、E、U 方向的结果见图2~6,可以看出,无论哪种观测数据各测站PPP 结果均显示U 方向改正量最大,原因在于固体潮主要是由日月引起地球表面升降造成的,因此固体潮模型对U 方向的改正量大于N、E方向。
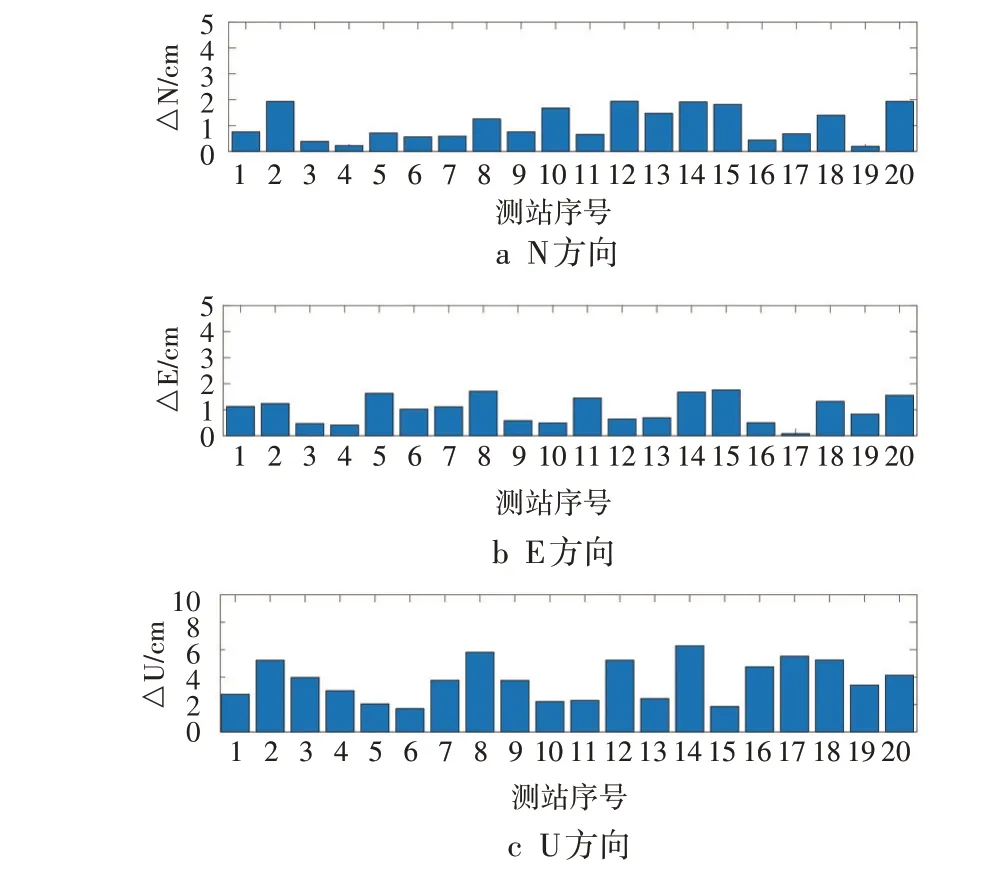
图2 GPS静态PPP三维方向误差
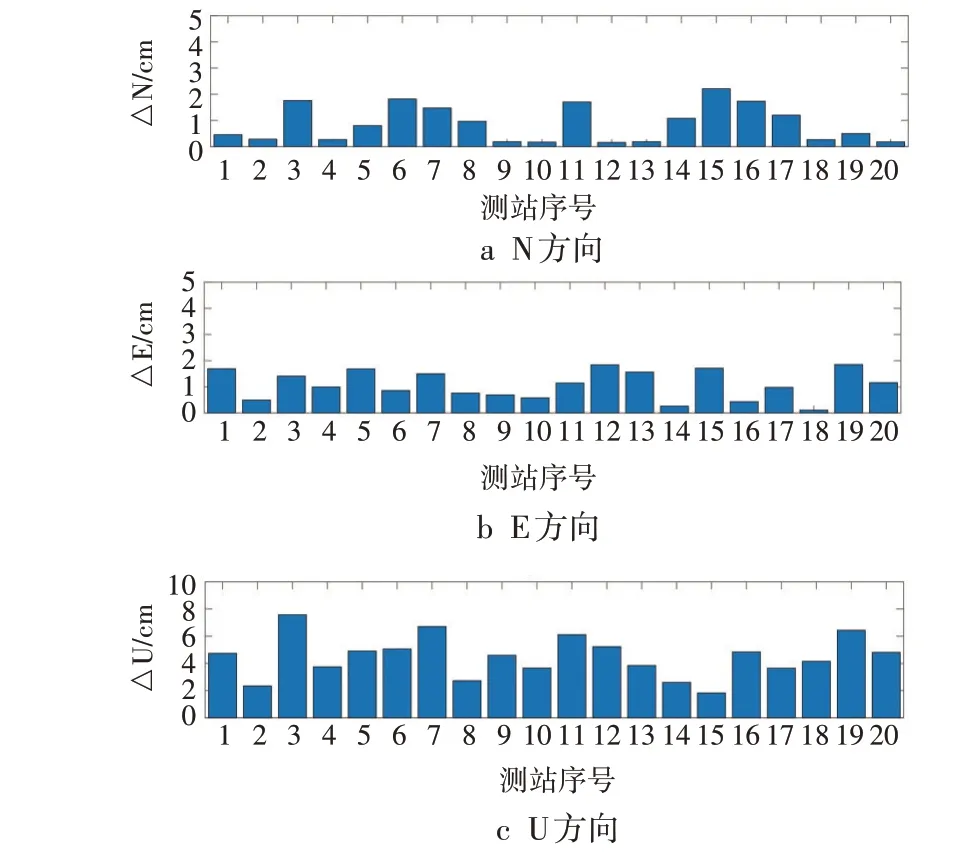
图3 BDS-2静态PPP三维方向误差
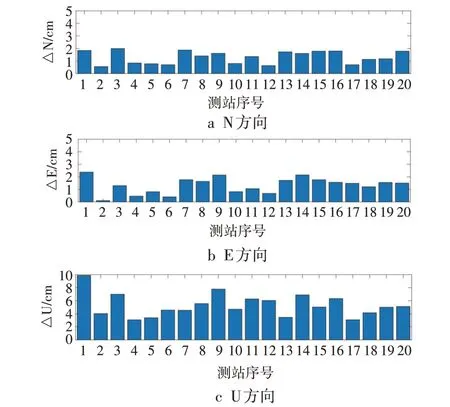
图4 BDS-3静态PPP三维方向误差
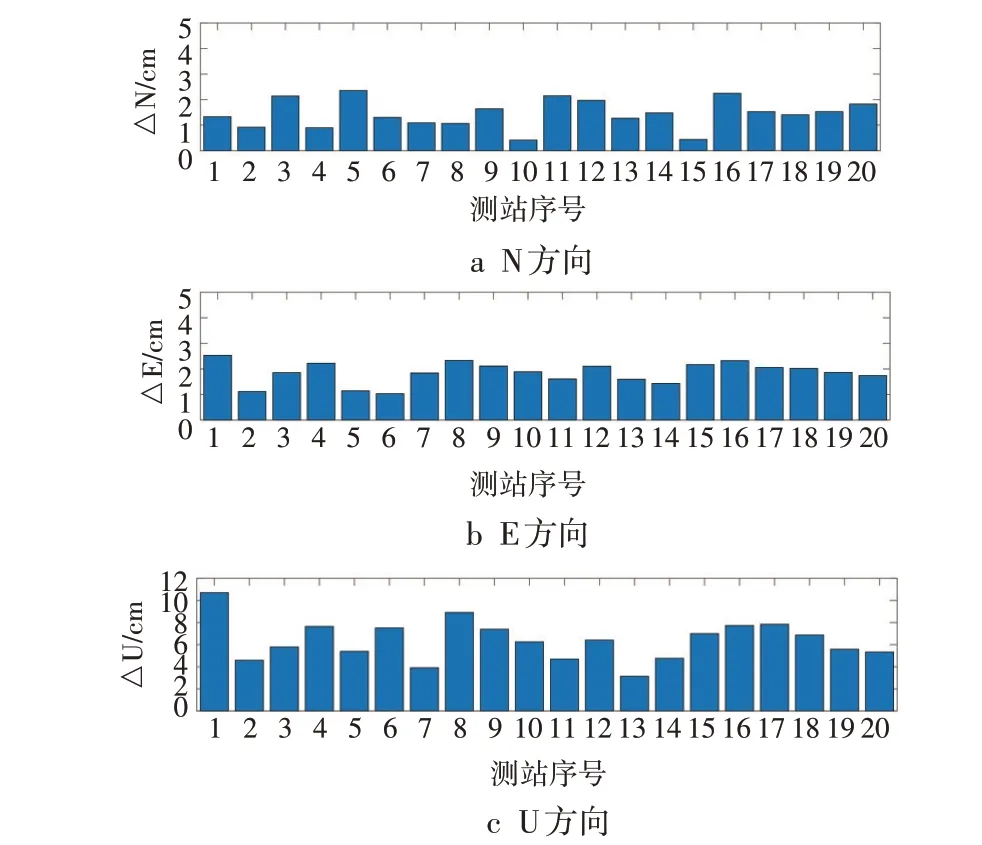
图5 BDS-2+BDS-3静态PPP三维方向误差
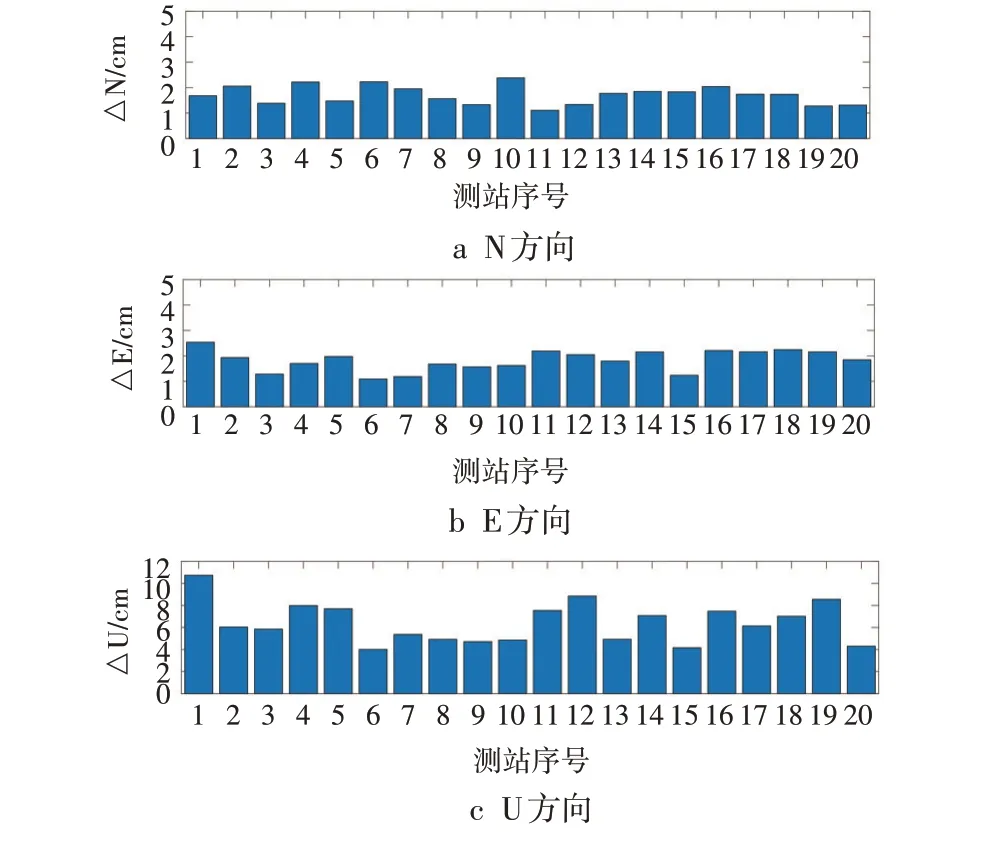
图6 GPS+BDS-2+BDS-3静态PPP三维方向误差
采用IERS2003固体潮改正模型使GPS PPP结果在N、E和U方向的最大改正量分别为1.94 cm、1.76 cm、6.28 cm,平均改正量分别为1.06 cm、1.01 cm、3.77 cm;使BDS-2 PPP 结果在N、E 和U 方向的最大改正量分别为2.20 cm、1.85 cm、7.57 cm,平均改正量分别为0.87 cm、1.09 cm、3.48 cm;使BDS-3 PPP结果在N、E 和U 方向的最大改正量分别为1.99 cm、2.37 cm、9.88 cm,平均改正量分别为1.30 cm、1.32 cm、5.29 cm;使BDS-2+BDS-3 PPP结果在N、E和U方向的最大改正量分别为2.36 cm、2.53 cm、10.70 cm,平均改正量分别为1.45 cm、1.85 cm、6.37 cm;使GPS+BDS-2+BDS-3 PPP 结果在N、E 和U 方向的最大改正量分别为2.38 cm、2.53 cm、10.73 cm,平均改正量分别为1.71 cm、1.83 cm、6.41 cm;固体潮改正模型对各系统下的PPP都有较大影响,最大可超过10 cm。对于同一系统的PPP,固体潮改正模型对不同测站PPP 结果改正量不同,可能是由于测站所处的三维地理空间位置不同,受地球弹性形变影响不同造成的;对于同一测站,固体潮模型对PPP结果在U方向的改正量优于N、E 方向,可能是由于PPP 过程中受卫星分布影响,U 方向误差最大,可供改正量较大,且固体潮模型是改正PPP过程中地球表面升降造成的误差。
4 结 语
本文对比分析了IERS2003 固体潮模型对GPS、BDS-2、BDS-3、BDS-2+BDS-3、GPS+BDS-2+BDS-3静态PPP的影响。结果表明,固体潮改正模型对U方向的改正量大于N、E 方向,其中U 方向最大改正量超过10 cm,测站所处地理位置会对模型改正量产生一定影响。因此,各系统PPP过程中应加入固体潮改正模型,以提高PPP精度。

