基于时变参数的灰色模型在变形监测中的应用

樊海青，马彦凤

（1.广东省国土资源测绘院，广东 广州 510500；2.广东省测绘工程有限公司，广东 广州 510700）

灰色系统通过建模、预测和分析等过程，能从已有少量信息中提取有价值的信息，为多个领域的组织决策和控制提供依据。灰色模型是在贫信息的情况下进行建模，对少量的原始观测数据进行处理，生成新的数据序列，并通过建立与求解白化微分方程得到预测模型，因此被广泛应用于变形监测工程中[1-5]。利用灰色GM(1,1)模型建立变形监测预测模型的方法较普遍，但也会出现模型的拟合与预测结果与实际值偏离较大的情况，因此相关学者采用灰色Verhulst模型、灰色二阶GM(2,1)模型、灰色GM(1,N)模型[6-8]等改进灰色模型进行数据分析，其中灰色二阶GM(2,1)模型能反映序列的趋势性变化，对数据的变化趋势提取更加有效。传统灰色模型在建立白化微分方程时，发展系数和灰色作用量为固定值，但在相关文献中提出，在同一时间序列中发展系数是固定量，而灰色作用量会随时间发生变化，即具有时变性质。本文以矿区地表沉降实测数据为例建立灰色模型，根据灰色作用量时变性质和灰色二阶GM(2,1)模型的优势，建立了传统灰色模型和基于时变参数的灰色模型；并对比了不同灰色模型沉降观测的预测结果和精度，以验证基于时变参数的灰色模型在沉降观测和模型预测过程中的可靠性与优越性。

1 基于时变参数的灰色模型

1.1 灰色模型

基于时变参数的灰色模型是由传统灰色模型改进而来，本文主要介绍灰色GM(1,1)模型和GM(2,1)模型。

1.1.1 灰色GM(1,1)模型

假设存在一组原始观测数据序列，即[3-4]

将原始数据进行累加，生成一次累加序列，即

由于一次累加序列存在指数型增长的趋势，满足式（3）灰微分模型：

根据最小二乘法求解灰微分方程的待求参数估值，即

将a1、b1以及初始条件x(1)( )1 =x(0)( )1 代入式（3），即可求解传统GM(1,1)模型的表达式：

还原数列得到原始观测序列的预测值，即

1.1.2 灰色GM(2,1)模型

不同于灰色GM(1,1)模型，灰色GM(2,1)模型除了对原始观测值进行了一次累加生成序列，还进行了一次累减生成序列。将式（1）中的原始数据进行累减，生成一次累减序列[9]，即

式中，a(1)x(1)(t)=x(0)(t)-x(0)(t-1)，t=2，3，…，n。

此时灰色GM(2,1)模型满足的灰微分模型为：

以最小二乘法求解式（8）的待求参数估值为：

1.2 基于时变参数的灰色模型建立

张振超[10]等为优化灰色GM(1,1)模型拟合与预测精度，通过时变参数优化灰作用量，建立了一种基于时变参数的GM(1,1)模型，采用线性时间函数代替固定不变的灰作用量。因此，本文在传统GM(1,1)模型和GM(2,1)模型的基础上分别建立了基于时变参数的灰色模型[10-12]。

若以时间的线性函数b3+b4t代替灰色作用量固定值，传统GM(1,1)模型的灰微分方程表达式为：

以最小二乘法求解式（10）的待求参数估值为：

将a1、b3、b4以及初始条件x(1)( )1 =x(0)( )1 代入式（10），即可求解基于时变参数的GM(1,1)模型表达式，即

同理，GM(2,1)模型的灰微分方程表达式为：

以最小二乘法求解式（13）的待求参数估值为：

采用式（6）还原数列，得到原始观测序列的预测值。

1.3 基于时变参数的灰色模型检验

基于时变参数的灰色模型以灰色模型为基础，因此应进行灰色模型检验，验证建立模型是否符合实际情况。检验指标以相对误差、后验方差比和小误差概率为主，判断灰色模型预测精度等级（表1）。

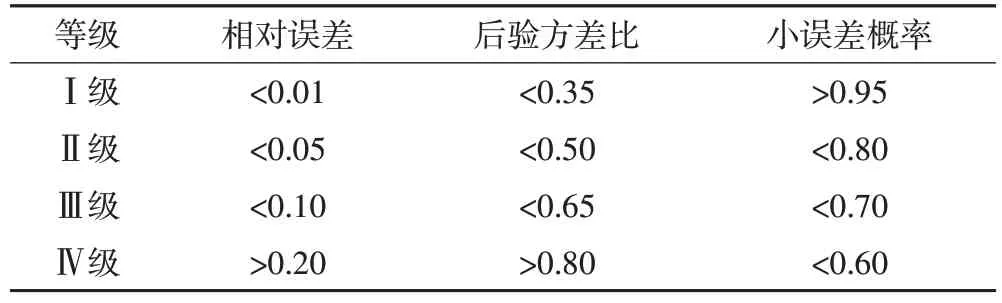
表1 灰色模型精度检验

2 实例分析

2.1 数据来源

本文以矿区采空区某走向观测线中93号、101号

沉降监测点为例，分别观测14期，采用电子水准仪按照国家三、四等水准测量规范要求对沉降监测点的垂直位移进行观测（表2、3）。为比较不同灰色模型的预测结果，本文设计了4 种灰色模型的算方案：①传统灰色GM(1,1)模型；②传统灰色GM(2,1)模型；③基于时变参数的GM(1,1)模型；④基于时变参数的GM(2,1)模型；将前10期作为拟合观测序列，后4期作为观测序列。

表2 93号监测点累计沉降值

表3 101号监测点累计沉降值

2.2 预测结果分析

2.2.1 传统灰色模型预测结果

根据传统灰色GM(1,1)和GM(2,1)模型建立的过程，编制灰色GM(1,1)和GM(2,1)模型的计算机语言程序，输入沉降监测点原始数据并建立灰色模型，得到预测结果以及预测值与实测值的残差值，见表4、5。

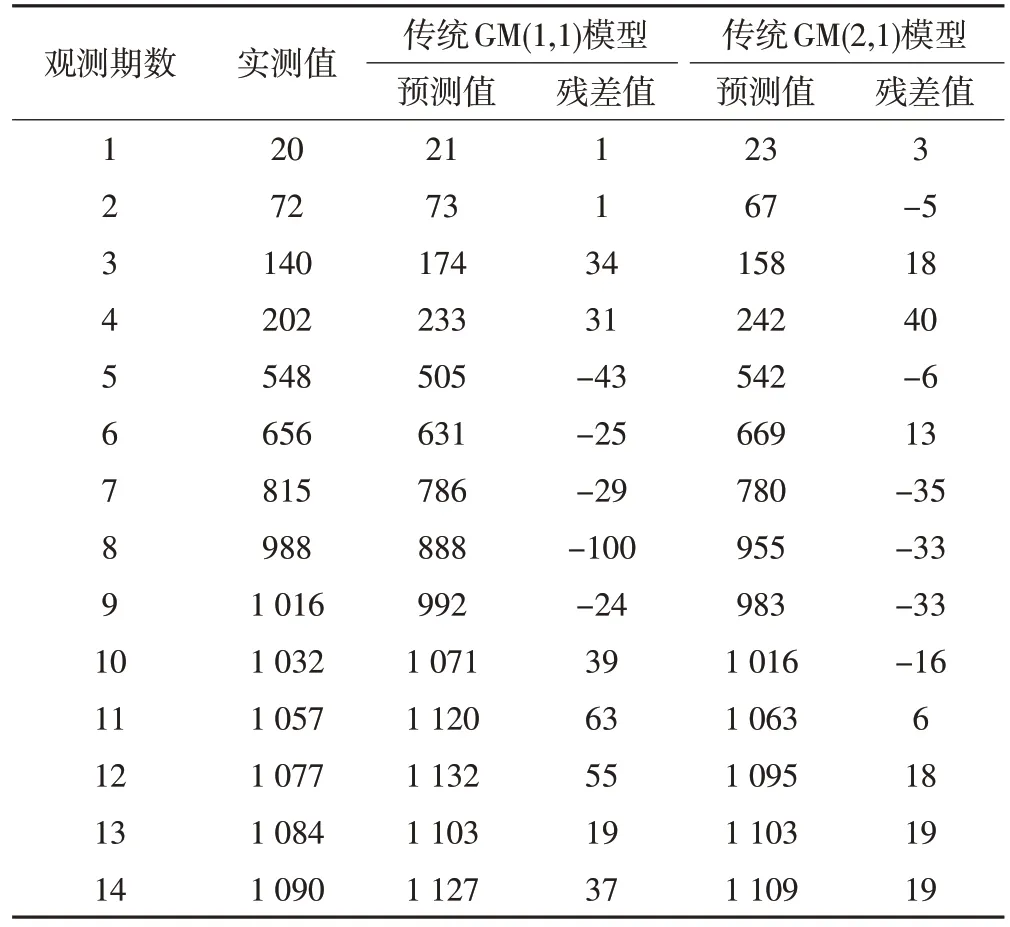
表4 93号监测点传统灰色模型预测结果/mm

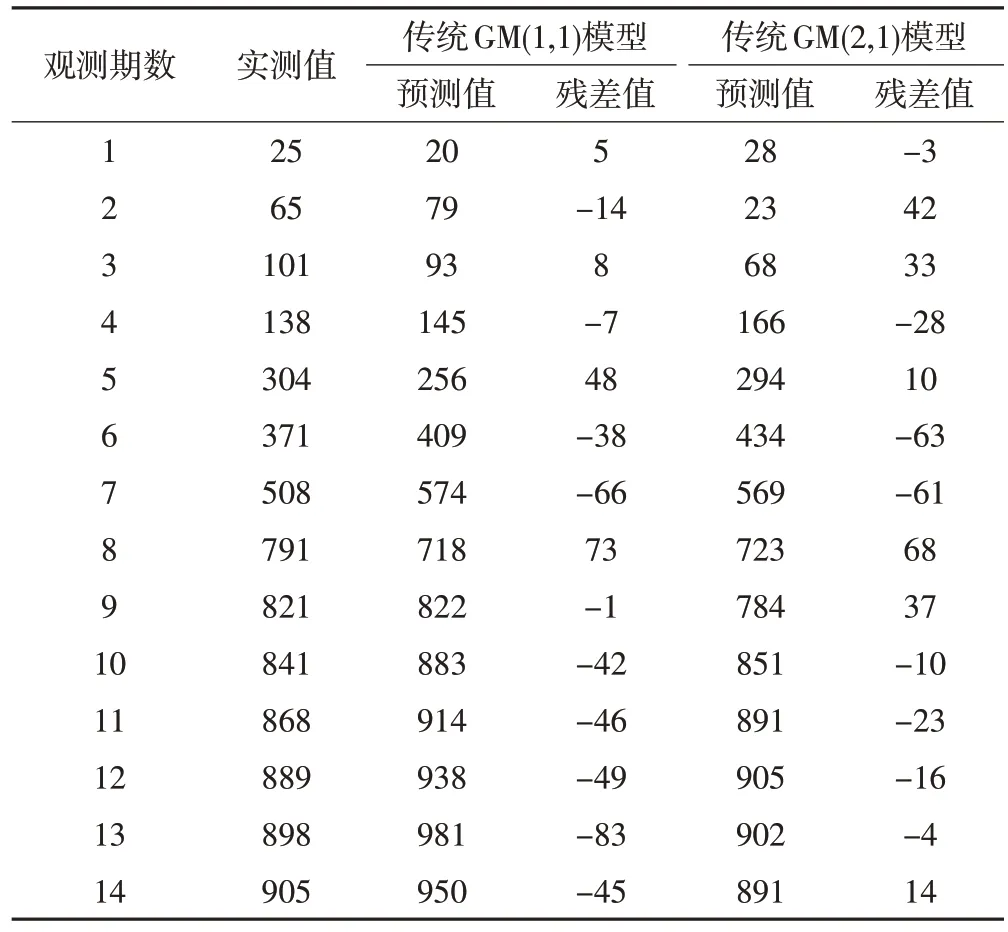
表5 101号监测点传统灰色模型预测结果/mm

2.2.2 基于时变参数的灰色模型预测结果

由于灰色作用量具有时变性质，本文建立基于时变参数的灰色GM(1,1)和GM(2,1)模型。根据时变参数灰色模型的建立过程，以沉降监测点为原始数据建立模型并计算，得到预测结果以及预测值与实测值的残差值（表6、7）。

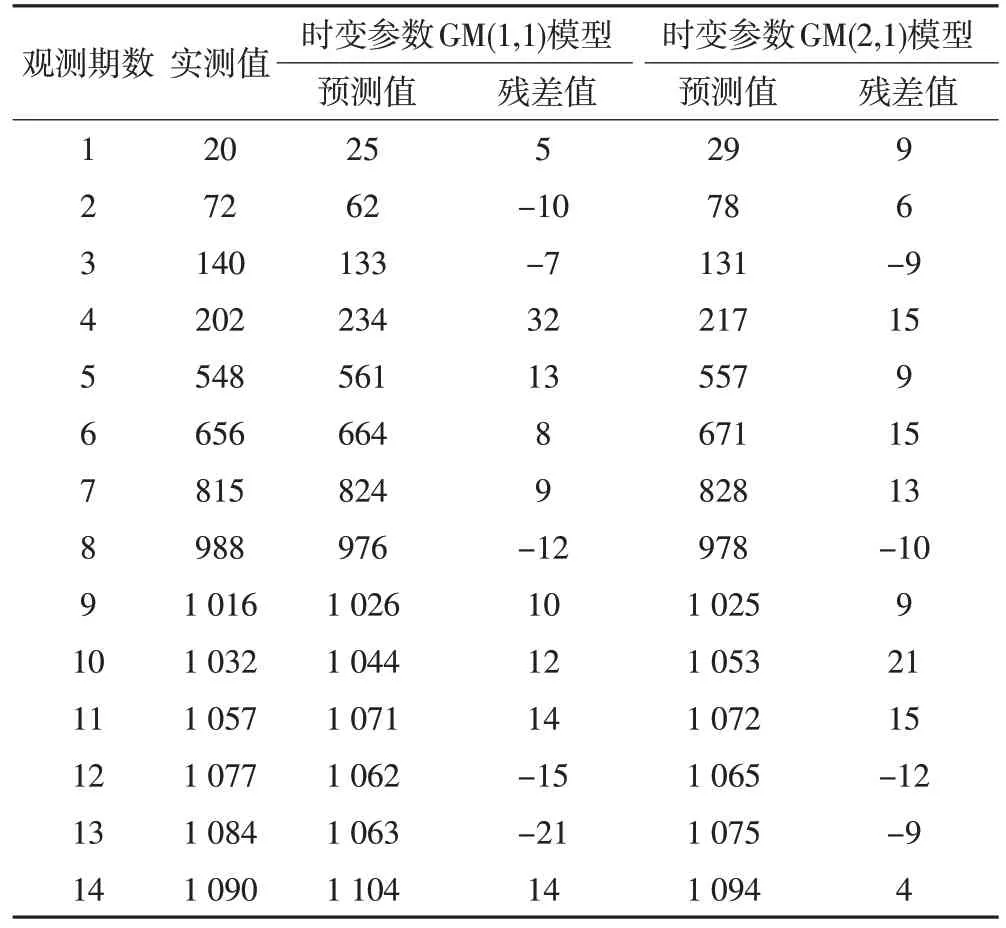
表6 93号监测点时变参数灰色模型预测结果/mm

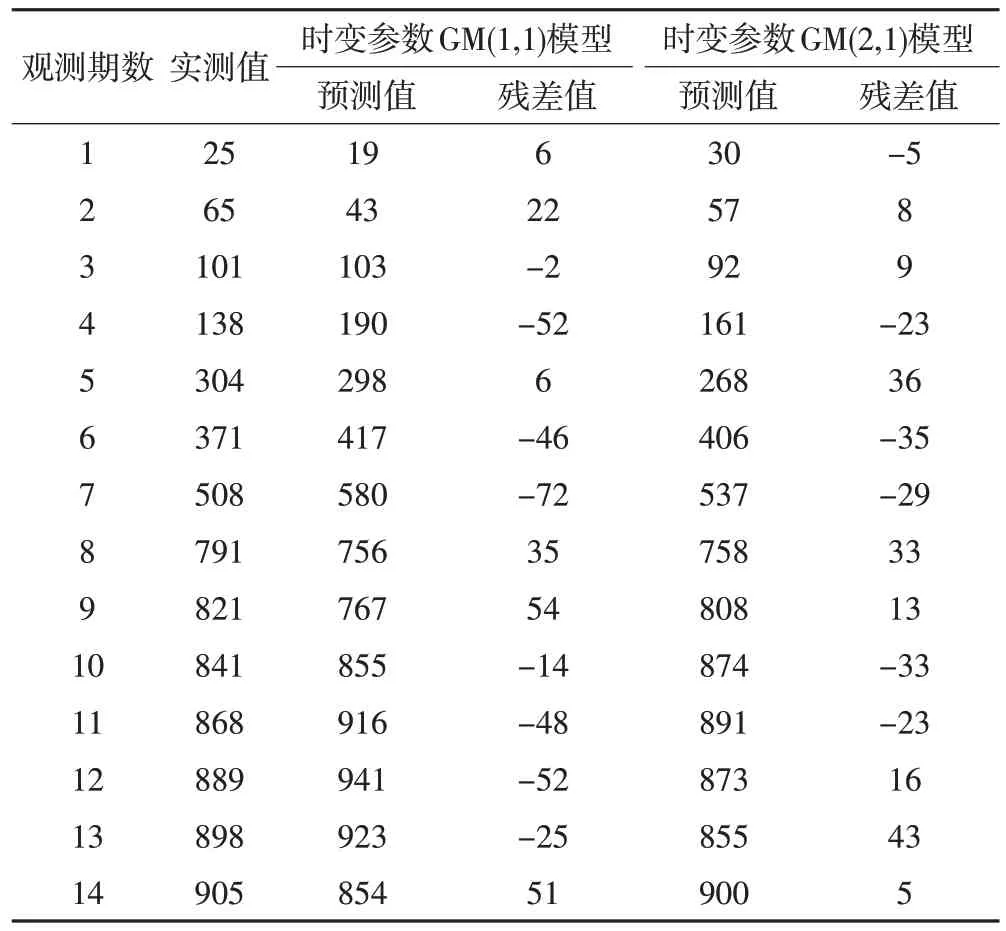
表7 101号监测点时变参数灰色模型预测结果/mm

2.2.3 不同模型预测结果对比分析

1）对于93 号监测点，方案①、②的残差绝对值最大值分别为100 mm、40 mm，均方根误差分别为11.53 mm、5.92 mm；对于101号监测点，方案①、②的残差绝对值最大值分别为73 mm、68 mm，均方根误差分别为12.12 mm、10.09 mm。在传统灰色模型中，方案②建立的灰色GM(2,1)模型求取的预测值均方根误差最小，预测精度最高。

2）对于93 号监测点，方案③、④的残差绝对值最大值分别为32 mm、21 mm，均方根误差分别为3.89 mm、3.18 mm；对于101 号监测点，方案③、④的残差绝对值最大值分别为72 mm、43 mm，均方根误差分别为10.86 mm、9.64 mm。在基于时变参数的灰色模型中，方案④建立的时变参数GM(2,1)模型求取的预测值均方根误差最小，模型预测精度最高。

3）根据表1 对基于时变参数的GM(2,1)模型进行精度评价，两个沉降监测点的精度检验等级均为Ⅱ级。

3 结 语

为提高灰色模型拟合与预测精度，本文将灰色作用量表示为随时间的变化的线性函数，建立了以时变参数优化灰色作用量的改进灰色模型；并通过建立不同灰色模型，对比分析了预测效果。结果表明，基于时变参数的GM(2,1)模型具有更好的预测效果，弥补了灰色作用量固定不变导致的预测精度差的问题。不足之处在于，在微分方程相关矩阵计算中，背景值基于前后紧邻值等权的原则，未对背景值进行优化，有待于进一步研究。