多模图像联合非局部滤波快速算法
杨元琴, 魏 宁, 董方敏
(湖北省水电工程智能视觉监测重点实验室(三峡大学),湖北 宜昌 443002)
多模图像联合非局部滤波快速算法
杨元琴, 魏宁, 董方敏
(湖北省水电工程智能视觉监测重点实验室(三峡大学),湖北 宜昌 443002)
提出一种新的基于非局部均值的多模图像滤波方法。在该方法中,对于噪声图像滤波采用非局部均值方法,其中对于噪声图像块之间灰度相似测度权重由另一幅图像引导计算。实验结果表明,该方法比基于局部的图像去噪方法如双边滤波算法有更好地去噪效果。通过构造联合积分图像对提出算法进行加速,与原始算法相比其显著提速两个数量级,加速算法的复杂度不受滤波器大小影响,易于在并行系统中实现。
图像去噪;联合双边滤波;非局部滤波;积分图像
图像在获取、传输和记录过程中不可避免地要受到各种噪声信号的干扰。在图像处理与计算机视觉领域,图像去噪是一项重要、基本的研究课题。去除图像噪声能提高图像视觉质量,是图像后续处理的前提,另外,图像去噪的方法在理论上与其他图像处理有着紧密的联系,研究图像去噪方法有一定的理论价值和实际意义。
多模图像是指对同一目标在不同条件(不同时间、不同传感器等)下获得的两幅或者两幅以上的图像,如对同一人体器官通过计算机断层成像(computer tomograph,CT)和核磁共振成像(magnetic resonance imaging,MRI)所产生的图像;对同一场景进行拍摄时带闪光灯和不带闪光的图像;用不同波段的成像设备获取的遥感图像等等。多模图像一方面可以反映不同空间结构信息形成、信息互补,另一方面图像之间存在着空间位置上的高度相关性可以方便对成像内容的结构进行深入分析。但多模图像由于受到成像带宽的限制,往往在有些波段的图像会存在较大的噪声干扰。多模图像联合去噪就是用噪声较小模态的图像信息来指导噪声较大模态的图像进行滤波处理。
多模图像联合去噪的方法基本都是以传统图像去噪方法作为基础进行改进而得到。传统的基于空间域图像去噪方法大致可以分为局部方法和非局部方法两种。局部去噪方法相对简单,主要是设计合适的滤波器与图像做卷积运算。其具代表性的局部联合去噪算法是由Petschnigg等[1]提出的联合双边滤波(joint bilateral filter)算法。该算法继承了双边滤波(bilateral filter)算法[2]的特点,在构造局部滤波器系数时不仅考虑了中心点与邻域点之间的空间距离,同时还考虑了中心点与领域点灰度值之间的相似程度。而不同于双边滤波,联合双边滤波算法在对一幅图像进行滤波时所使用的滤波器系数由另一幅图像来引导计算。该算法在对闪光与非闪光图像进行联合处理时取得了较好的效果。联合双边滤波具有将多种信息进行结合并完成滤波的特点,同时还被应用到不同变换域信息联合去噪上,如,Knaus和 Zwicker[3]提出了双域去噪(dual denoising)。该算法通过联合双边带滤波将频域和时域滤波的结果进行互补获得了很好的去噪效果。Yu 等[4]提出在空间域使用双边滤波并在变换域使用小波变化,通过将两者的结合得到了比较好的去噪效果。邱宇等[5]将曲线波与双边滤波算法有机结合,取得了较好效果。蔡超等[6]将多分辨率分析概念引入到双边滤波中,根据噪声强弱,在不同尺度下采用不同的参数可以达到比较好的去噪效果。余博等[7]对相关参数的选取进行了研究,提出了一类自适应的改进双边滤波算法,基本实现了参数的自适应选取。近年来,由于联合双边滤波受到广泛关注,其计算速度的劣势凸显。Zhang等[8]提出了针对联合双边滤波的加速算法,并通过构造联合积分直方图达到了对原始算法的加速,能够在常数时间获得与原始算法近似的结果。
双边滤波算法的加权系数不仅考虑了像素间的空间距离,也考虑了亮度相似度,因此能更好地实现图像的去噪和边缘保留[9-11],但其存在算法鲁棒性的问题。由于灰度测度权重的获取是通过两个独立像素的灰度差,当两个像素均受到噪声污染时,灰度测度的稳定性就会降低,且噪声越大稳定性就越差。Buades等[12]提出的非局部均值算法(NL-means)能够解决这一问题,该算法在计算灰度测度权重时不再使用当前像素点与邻域像素点的相似度,而是使用以这两个像素为中心的邻域块之间的相似度。由于图像通常都包含丰富的纹理,且重复出现,因此加权平均的像素点可以扩展到整幅图像而不必局限于图像的局部。相比于双边滤波,非局部均值算法能够获得更准确的灰度测度权重。但是,由于非局部均值算法需要计算图像块之间的相似性,而且图像块的搜索区域可以扩展到整幅图像,因此算法的复杂度很高。
在对多模图像去噪的过程中,如果能将多幅图像之间的这种非局部的相似性联合起来进行平均系数设计,其去噪结果能够对边缘细节和重复纹理细节得到很好地保持。目前基于非局部联合去噪研究较少,本文提出了一种联合非局部滤波算法,该算法旨在保持非局部滤波算法的优势,在对一幅图像进行全局滤波时,其滤波权重由参考图像中所有的相似图像块决定。该算法对于含有周期性纹理的闪光与非闪光图像,或者是存在着大量平坦区域的多模医学图像,相比于联合双边滤波算法具有更好的去噪效果。另外,为了解决非局部算法复杂性高的问题,本文构造了相应的联合积分直方图对算法进行了加速。通过理论分析表明,加速算法较原始算法能够提高近2个数量级。
1 联合非局部滤波

其中,相似测度权值{w(i,j)}j依赖于像素i与j之间的相似性,并满足。相似测度权重{w(i,j)}j不同于原始的双边滤波那样通过原始噪声图像来计算,而是通过联合参考图像I的信息计算得到。在滤波时任意两个像素之间的相似性是以这两个像素为中心的邻域块之间的相似性决定,邻域块灰度值向量之间的相似性通过欧氏距离计算,即:

其中,p为以当前像素为中心的邻域半径。则式(1)中的权重定义为:
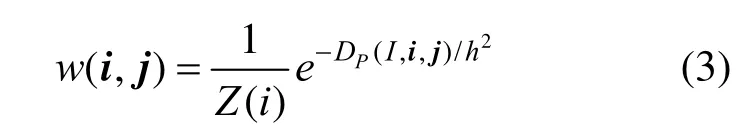
2 算法加速
用所提出算法进行滤波,由于其过程存在大量的冗余计算,因此非常耗时。假设给定两个固定像素,并通过式(2)计算两个像素之间的相似性时,部分图像子块的平方差求和会被反复多次计算其他固定像素之间相似性,其计算冗余延长了计算时间。本文提出了一种基于积分直方图的加速算法避免上述冗余,有效提高了计算效率。
假设计算图1(a)中的两个像素i,i+t之间的相似性,t代表两像素点在空间的平移向量。将图像I平移t个单位得到图像It。如图1(b)所示,可以看到每一对有着相同位移 t的图像块之间的相似性DP(I,i,i+t)可以通过对图像(I–It)2中相应块中对应块的元素进行求和得到。
为了避免对(I–It)2中的元素重复求和,构造了积分图像Jt,如图1(c)所示,即:


图1 当比较两个像素的相似性时,对于每个可能的位移t构造积分图像((a) 相似像素位移相差t;(b) 计算矩阵(I–It)2;(c) 构造积分图像Jt)
规定 J(0,0)=0。这样,任意图像块之间的距离DP(I,i,i+t)能够通过积分图像 Jt快速地计算得到:

所提出的加速算法可最大程度地减少乘法和加法重复计算次数。假设给定图像为N×N,在相似性计算时的邻域大小为P×P,可以发现直接使用原始暴力方法计算的算法复杂度为O(N4×p2)。通过加速计算之后,图像Jt的大小随着向量t的增加而减少。加速之后算法的复杂度降为O(N4/4)。值得注意的是,加速方法其算法复杂度不依赖于图像相似块的大小P,这样扩展了算法的适用性。另外,可以看到主要计算量来自于(I–It)2的计算以及 Jt的构造。由于参数都是相互独立的,因此该算法能够通过并行计算进一步提高执行效率。
联合非局部滤波快速算法的步骤如下:
算法:联合非局部滤波快速算法
步骤1. 对于每一个可能的平移量t,用参考图像I构造平方差图像(I–It)2。
步骤 2. 对每一个(I–It)2通过式(4)计算得到积分图像Jt。
3 实验与结果
为了验证本文算法的性能,将实验结果与联合双边滤波方法[1]的结果进行比较。之所以不与基于积分直方图的联合双边滤波方法[8]的结果相比较,是因为后者是对前者的加速改进,尽管得到了几乎一致的实验效果,但是图像质量在灰度量化中还是有所损失。
实验用3个数据集进行测试。所提出方法实验结果与联合双边滤波方法的结果比较如图2所示。图2中前两行分别是对“lamp”和“carve”图像[1]的去噪处理。其中每一行的第1列为非闪光图像,第2列为对应的闪光图像,第3列为联合双边滤波方法去噪结果,第4列为所提出方法的去噪结果。一般闪光图像具有清晰的轮廓边缘和高对比度的边缘信息,而非闪光图像具有更自然的环境光氛围和更细腻的纹理细节,但由于感光度低含有较大噪声。为了突出两种算法滤波的效果,实验中在原始非闪光图像加入PSNR=45 dB的高斯噪声。如图1所示,两种方法都得到了相比单模式图像更好地去噪效果。但是对于重复纹理较为密集的“lamp”图像所提出的方法对于稻草的细节纹理边缘进行了更好地保持,去噪效果显著。同时对于细节纹理较多的“carve”图像,所提出的方法在去除噪声的同时能够更好地保持了瓦罐表面和背景墙壁的纹理。
图2的最后一行是从Brainweb上获得的模拟脑部MRIT1和T2多模图像。结果显示对于该组图像两种方法的去噪效果基本持平,本文提出的方法并没有显示出明显的优势。

图2 实验结果(从第1列至第4列:非闪光图像(噪声图像);闪光图像(参考图像);联合双边滤波方法的去噪结果;所提出方法的去噪结果)
另外,图3比较了本文所提出方法在不同参数下的实验结果。其中列表示参数h,h是式(3)中的方差,随着h的增加图像平滑程度越强;行代表邻域块p的大小变化,结果显示随着块的增大,图像的平滑程度减弱,这是由于当邻域块过大时,对于像素灰度的度量误差就会过大,去噪效果就会更差。从本文的测试数据可以观察得到,当邻域块大小取p=5时是比较合适的。

图3 所提出方法在不同参数下的结果(从第1列至第3列:h=10、20、30;从上到下:p=3、5、7)
图4为不同噪声强度的图像去噪后的结果对比。第1列表示不同的噪声强度的图像,从上至下PSNR= 45,20,10 dB。第2、3列分别表示联合双边滤波方法与所提出方法得到的去噪结果(其中均选取试验中效果最好的参数)。结果显示所提出方法在细节部分,特别在尖锐边缘区域、带状纹理等情况下能够得到比联合双边滤波方法更好地去噪效果。

图4 不同噪声强度下去噪结果对比(第1列为噪声图像;第2列为联合双边滤波方法的去噪结果(从上至下参数设置为p=5,σs=5,σr=2、3、6);第3列是本文方法去噪结果(参数设置为:p=5,h=10、15、20))
4 结 论
本文提出了一种针对多模图像去噪的联合非局部滤波算法。实验表明,该算法的去噪效果要优于传统的局部去噪算法,特别是对于复杂的重复性的纹理图像更能体现出其优势。此外本文针对非局部算法计算复杂度高的问题,提出的基于联合积分直方图的加速算法,通过加速能够将计算复杂度降低2个数量级,从而有效提高了算法的计算效率及适用范围。
[1] Petschnigg G, Szeliski R, Agrawala M, et al. Digital photography with flash and no-flash image pairs [J]. ACM Transactions on Graphics, 2004, 23(3): 664-672.
[2] Tomasi C, Manduchi R. Bilateral filtering for gray and color images [C]//Proceedings of the 1998 IEEE International Conference on Computer Vision. Bombay, India,1998: 839-846.
[3] Knaus C, Zwicker M. Dual-domain image denoising [C]// Proceedings of International Conference on Image Processing. Melbourne, Austrilia, 2013: 440-444.
[4] Yu H, Zhao L, Wang H. Image denoising using trivariate shrinkage filter in the wavelet domain and joint bilateral filter in the spatial domain [J]. IEEE Transactions on Image Processing, 2009, 18(10): 2364-2369.
[5] 邱宇, 王世元, 余勇志. 一种基于曲线波的改进自适应交叉双边滤波方法[J]. 西南师范大学学报: 自然科学版, 2013, 38(2): 96-105.
[6] 蔡超, 丁明跃, 周成平, 等. 小波域中的双边滤波[J].电子学报, 2004, (1): 128-131.
[7] 余博, 郭蕾, 钱晓亮, 等. 一种新的自适应双边滤波算法[J]. 应用科学学报, 2012, 30(5): 517-523.
[8] Zhang K, Lafruit G, Lauwereins R, et al. Constant time joint bilateral filtering using joint integral histograms [J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2012, 21(9): 4309-4314.
[9] 张闯, 迟健男, 张朝晖, 等. 基于边缘检测与双边滤波的彩色图像去噪[J]. 电子学报, 2010, 38(8): 1776-1783.
[10] 叶仕通. 结合阈值去噪与边缘优化的图像增强算法[J].图学学报, 2014, 35(4): 571-576.
[11] 戚晓伟, 陈秀宏. 改进的 Otsu 方法的双边滤波边缘检测算法[J]. 计算机工程与应用, 2012, 48(31): 150-155.
[12] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising [C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2005, 2005: 60-65.
Accelerated Multimodal Images Joint Non-local Filtering
Yang Yuanqin,Wei Ning,Dong Fangmin
(Hubei Key Laboratory of Intelligent Vision Based Monitoring for Hydroelectric Engineering, China Three Gorges University, Yichang Hubei 443002, China)
In this paper, a novel non-local averaging based multimodal image filtering method is provided. In the method, the mean average for filtering the noisy image is computed non-locally and weights for average is jointly guided by the reference image taken from another imaging device. The experiment results show that the proposed method is better than state of the art joint bilateral filter, especially in the case of the periodic texture is involved in the images. Furthermore, an acceleration algorithm is proposed by constructing integral histograms, speeding up by factor of about 2 order compared with the brute-force method. In addition, the algorithm is independent of the size of the filter, and easy to be implemented on parallel system.
image denoising; joint bilateral filter; non-local filter; integral image
TP 399
10.11996/JG.j.2095-302X.2016010074
A
2095-302X(2016)01-0074-05
2015-06-15;定稿日期:2015-09-14
国家自然科学基金项目(61202141);国家自然科学基金面上项目(61272236)
杨元琴(1990–),女,湖北宜昌人,硕士研究生。主要研究方向为计算机图像处理。E-mail:747640839@qq.com
魏宁(1980–),男,甘肃兰州人,副教授,博士。主要研究方向为机器视觉、计算机图形学。E-mail:weininglz@163.com

