一种区间灰数的优化预测模型

胡大红

(汉口学院 计算机科学与技术学院,湖北 武汉 430000)



一种区间灰数的优化预测模型

胡大红

(汉口学院 计算机科学与技术学院,湖北 武汉 430000)

由于灰数间的代数运算会导致结果灰度的增加，所以对区间灰数进行建模时，为避免区间灰数的代数运算，本文将区间灰数序列转化为白部序列和灰部序列，再对白部序列和灰部序列分别建立灰色优化预测模型，最后通过实例证实了此方法的有效性与可行性.

灰色系统理论;区间灰数;预测模型;白部序列;灰部序列

灰色预测模型是对少样本，贫信息系统进行建模的重要预测模型.自提出以来，主要应用于离散数据的建模预测[1-3].目前，由于灰数的代数运算体系还不完善，灰数间的代数运算会导致结果灰度的变化[4]，对于连续的区间灰数，直接对区间灰数构建预测模型尚有难度.文献[5]探讨了灰色预测模型在技术市场上的应用.现阶段，对区间灰数进行建模的方法主要还是将区间灰数转化为离散数据，再进行建模，最后还原.文献[6-7]对区间灰数预测模型的构造进行了研究，文献[8]提出了基于灰数带及灰数层的区间灰数预测模型，文献[9]探讨了在白化权函数已知的条件下的区间灰数的预测模型构建问题.本文将区间灰数转化为白部和灰部两部分，再对白部和灰部分别建立文献[10]所提出的灰色优化预测模型，模拟效果和预测效果都较好，具有较高的应用价值.

1 区间灰数的白部与灰部的定义

定义1 既有上界ak又有下界bk的灰数称为区间灰数，记为⊗k， 其中ak≥bk,k=1,2,…,n.若ak=bk，则区间灰数就变成了白数，即白数是一种特殊的区间灰数.

2 优化的灰色预测模型的构建

原始GM(1,1)灰微分方程为:

(1)

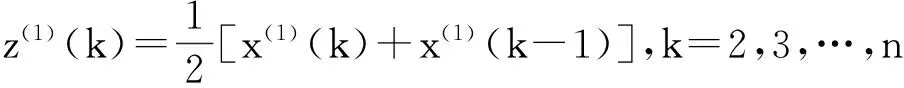
对应的白化微分方程:

(2)

方程(2)在[k-1,k]上积分，得:

(3)

与方程(1)对比，有:

(4)

由积分中值定理可知:

(5)

又因为灰色白化微分方程的时间响应式为:

(6)

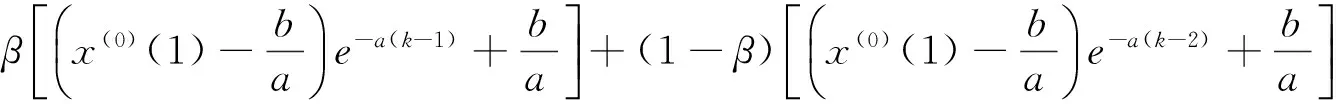
(7)

3 优化灰色预测模型的参数估计

建立优化的灰微分方程:

(8)

则有:x(0)(k)+a[βx(1)(k)+(1-β)x(1)(k-1)]=b，

表2 白部序列的模拟和预测精度

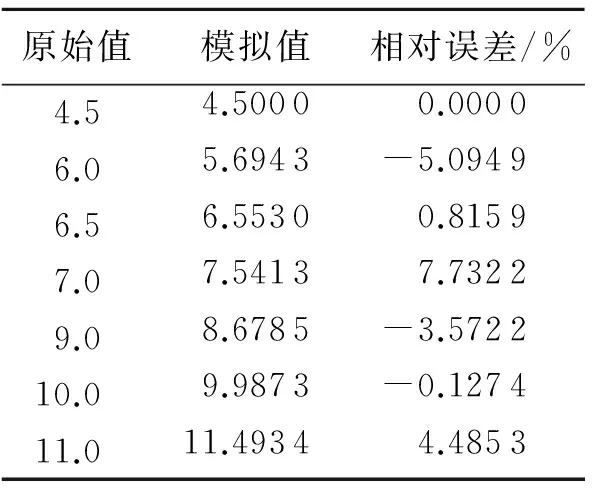
表3 灰部序列的模拟和预测精度

4 实例分析

以文献[11]中的区间灰数如表1所示，本文以表1中的区间灰数为例，建立本文所提出的优化灰色预测模型.

表1 某市2003-2009年的外来务工数量 万人

该市2003-2009年的外来务工数量的区间灰数序列为X(⊗)=([49，58]，[58，70]，[75，88]，[89，103]，[114，132]，[135，155]，[161，183])，区间灰数的白部序列为⊗(0)=(53.5,64,81.5,96,123,145,172)，区间灰数的灰部序列为C(⊗)=(4,5,6,6.5,7,9,10,11)对区间灰数的白部序列和灰部序列的前6个数据分别建立优化灰色预测模型，后一个数据进行预测.

其中表2中前六行是白部序列的模拟值和模拟相对误差，平均模拟相对误差为1.623 1%.最后一行是预测值及预测相对误差，预测相对误差为4.3502%.

其中表3中前6行是灰部序列模拟值和模拟相对误差，平均模拟相对误差为2.890 4%.最后一行是预测值及预测相对误差，预测相对误差为4.485 3%.

从上述表1～3可以看出优化模型的模拟精度和预测精度均介于1%与5%之间，拟合效果较好，可以用于此种方法对区间灰数进行预测与决策.

5 结束语

由于灰数间的代数运算会导致结果灰度的变化，而目前灰色系统理论尚没有解决这一问题,所以灰色系统理论研究者在研究区间灰数的建模问题时，一般把区间灰数或灰数序列转化为实数或实数序列来规避灰数之间的代数运算，再进行建模预测.本文通过将区间灰数序列转化为白部序列和灰部序列，再分别对白部序列和灰部序列建立优化的灰色预测模型，模拟效果与预测效果均较好，对区间灰数的建模进行了有益的探索.

[1] 肖新平,刘军,郭欢.广义累加灰色预测控制模型的性质及优化[J].系统工程理论与实践，2014，34(6)：1547-1556.

[2] 郭晓君，刘思峰，方志耕，等.灰色GM(1,1)模型与自忆性原理的耦合及应用[J].控制与决策,2014,29(8):1447-1452.[3] 王正新.时变参数GM(1,1)幂模型及其应用[J].控制与决策,2014,29(10):1828-1832.

[4] 刘思峰,党耀国,方志耕，等.灰色系统理论及其应用[M].3版.北京：科学出版社,2004：10-16.

[5] 赵娟,付强.基于灰色预测模型与线性回归模型的全国技术市场成交合同金额分析[J].西南民族大学学报(自然科学版),2015,41(2):251-254.

[6] 曾波,刘思峰.基于灰数带及灰数层的区间灰数预测模型[J].控制与决策,2010,25(10):1585-1588.

[7] ZENG B,LIU S F,XIE N M.Prediction model of interval grey number based on DGM(1,1)[J].J of Systems Engineering and Electronics,2010,21(4)：598-603.

[8] 曾波,刘思峰.一种基于区间灰数几何特征的灰数预测模型[J].系统工程学报,2011,26(2):174-180.

[9] 曾波,刘思峰,崔杰.白化权函数已知的区间灰数预测模型[J].控制与决策,2010,25(12):1815-1819.

[10] 徐宁,党耀国,丁松.基于误差最小化的GM(1,1)模型背景值优化方法[J].控制与决策,2015,30(2):283-288.

[11] 孟伟,刘思峰,曾波.区间灰数的标准化及其预测模型的构建与应用研究[J].控制与决策,2012,27(5):773-776.

责任编辑：时 凌

Optimization Prediction Model for Interval Grey Number

HU Dahong

(College of Computer Science & Technology,Hankou University,Wuhan 430000,China)

The algebraic operations between interval grey numbers will lead to the results to be greyer,so in this paper the interval grey number sequences are divided into white part and grey part in order to avoid algorithm of interval grey number when the grey prediction model is proposed,and the optimization prediction models are proposed respectively.Finally,an example is given to show the effectiveness and feasibility of the method.

grey system theory; interval grey number;prediction model; white part sequence;grey part sequence

2016-08-11.

湖北省教育厅科研项目(B2015504).

胡大红(1974- )，女，硕士,副教授,主要从事灰色系统理论及其应用的研究.

1008-8423(2016)03-0315-03

10.13501/j.cnki.42-1569/n.2016.09.018

N941.5

A