Reich-Takahashi迭代序列的收敛性

刘 辉

(黑龙江财经学院)



Reich-Takahashi迭代序列的收敛性

刘 辉

(黑龙江财经学院)

研究了在具有一致Gteaux范数的Banach空间框架下， Reich-Takahashi迭代序列在一致L-Lipschitz非扩张映射T的不动点的收敛性问题，其中压缩映射Sn(z)=(1-dn)x+dnTnz的不动点序列{zn}强收敛于T的这一不动点.

Banach空间；Reich-Takahishi迭代序列； Gteaux可微

0 引言

定义1 设D是E非空闭凸子集，x0∈D是一给定的点，T:D→D是一映射

(1)如果T是一致L-Lipschitz非扩张映射，则由下式定义的序列{xn}：

(1)

及由下式定义的序列{xn}

(2)

均称为伪Reich-Takahashi迭代序列，其中{αn},{βn},{δn},{σn}均是[0,1]中的序列且αn+δn=1，βn+σn=1.

(2)如果T是非扩张映射，则序列{xn}：

(3)

及由下式定义的序列{xn}：

(4)

都称为Reich-Takahashi迭代序列，其中{αn},{βn},{δn},{σn}均是[0,1]中的序列且αn+δn=1，βn+σn=1.

引理1[3]假设E是一实Banach空间，J:E→2E*是对偶映射，则对x,y∈E,有如下的结论成立：

(1) ‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉,

j(x+y)∈J(x+y);

(2) ‖x+y‖2≤‖x‖2+2〈y,j(x)〉,

j(x)∈J(x).

引理2[4]令{an},{bn},{cn}是三个非负实数序列，且满足以下条件：若存在自然数n0满足

an+1≤(1-λn)an+bn+cn,∀n≥n0

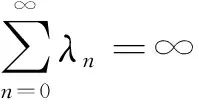
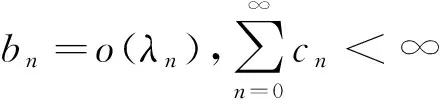
引理3[5]设{an},{bn}是两个非负实数序列，且设存在自然数n0满足

an+1≤(1-λn)an+bn,∀n≥n0

an→0(n→∞)

1 Reich-Takahashi迭代序列的收敛性

设F(T)非空，再设{αn},{βn},{δn},{σn}是[0,1]中给定的序列，αn+δn=1,βn+σn=1,且满足条件：

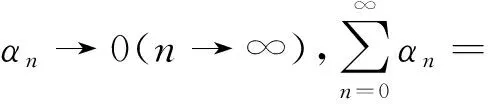
对给定的x∈D及n≥1，定义压缩映射Sn:D→D

Sn(z)=(1-dn)x+dnTnz,

其中

(5)

由Banach压缩原理，设zn是Sn的唯一的不动点，于是zn满足：

zn=Sn(zn)=(1-dn)x+dnTnzn,n≥1.

(6)

如果下面条件满足：

(1){zn}强收敛于某一z∈F(T);

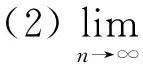
则由(1)式的序列{xn}强收敛于z∈F(T).

证明 由条件(1)，{yn}是有界的，又由条件(2)，{zn}强收敛于某一z∈F(T)，于是由(1)式有

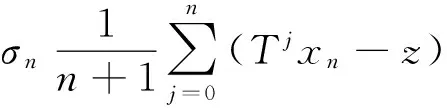
αn‖x-z‖+δnL2‖xn-z‖≤M1.

(7)

其中

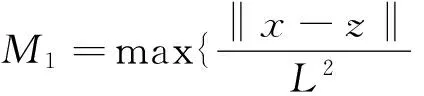
另外，因为

‖Tnxn-z‖≤L‖xn-z‖,∀n≥0

(8)

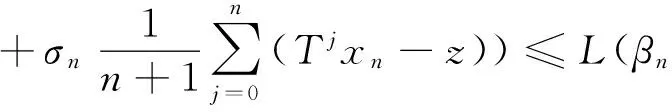
(9)

由(7)，(8)，(9)知{xn},{Tnxn}，{Tnyn}均为有界列.另由(1)式及T的渐近非扩张性有：

‖yn-z‖ =‖βn(xn-z)+

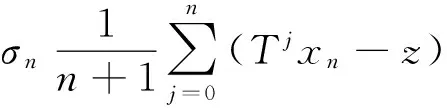
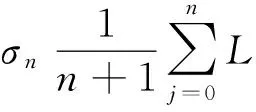
σnL‖xn-z‖≤L‖xn-z‖

(10)

另由命题1知，正规对偶映射J:E→2E*在E的每一有界集上由E的范数拓扑到E*上的弱*拓扑是一致连续的.故由(1)式及引理1，有

‖xn+1-z‖2=‖αn(x-z)+

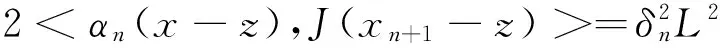
(11)

现在考察(11)式右端的第一项，由(10)式有

δn‖xn-z‖2+δn(L4-1)‖xn-z‖2≤δn‖xn-z‖2+(L4-1)‖xn-z‖2≤

(1-αn)‖xn-z‖2+M2

(12)

其中

现在考察(11)式右端的第二项，由(6)式有

xn-zm=xn-(1-dm)x-dmTmzm=(1-dm)(xn-x)+dm(xn-Tmzm),∀n≥0,∀m≥1

(13)

由引理1及(13)式有

‖xn-zm‖2=‖(1-dm)(xn-x)+

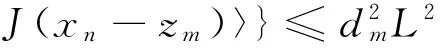
2(1-dm)‖xn-zm‖2+2(1-dm)〈zm-x,

J(xn-zm)〉

(14)

因{xn},{zm}有界，记

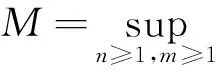
(15)

对(14)式化简后得

(16)

其中

由条件(3)及(15)知当n→∞时，关于m∈N一致地有

(17)

于是由(16)，(17)及定理1的条件(4)有

又因dm→1(m→∞)，从而有

(18)

另由(15)知‖zm-xn‖≤M,‖xn-z‖≤M,∀n≥0,m≥1.现取r≥2M，并记Br={x∈E:‖x‖≤r}.由定理的假定E是一实Banach空间，其范数是一致Gteaux可微的，故由命题1知，对偶映射J:E→2E*是单值的，而且在闭球Br上是由E 的范数拓扑到E*的弱*拓扑一致连续的.于是对任给的ε>0，存在δ(ε)>0，使得对任意的x,y∈Br，当‖x-y‖<δ时，对一切u∈E一致地有

|〈u,J(x)-J(y)〉|<ε

(19)

因zm→z，故存在正整数N0使得‖zm-z‖<δ,∀m>N0.另由(13)知，对任意的n≥0及任意的m≥1,xn-z∈Br,xn-zm∈Br.因‖(zm-xn)-(z-xn)‖=‖zm-z‖<δ,∀m>N0,于是由(17)对一切u∈E一致地有

|〈u,J(zm-xn)-J(z-xn)〉|〈ε,∀m〉N0,n≥0

(20)

于是当m>N0,n≥0时，有

〈x-z,J(xn-z)〉=〈x-z,J(xn-zm)-J(xn-zm)〉+〈x-zm+zm-z,J(xn-zm)〉≤

|〈x-z,J(xn-z)-J(xn-zm)〉|+〈x-zm,J(xn-zm)〉+〈zm-z,J(xn-zm)〉=ε+〈x-zm,J(xn-zm)〉+‖zm-z‖·‖xn-zm‖≤ε+

〈x-zm,J(xn-zm)〉+‖zm-z‖M.

于是有：

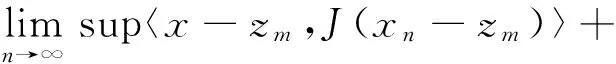
(21)

在(21)中再让m→∞取上极限，并注意到(15)，即得：

由于ε>0的任意性，有

(22)

令ωn=max{〈x-z,J(z-xn)〉,0}，由(22)易知0≤ωn，而且ωn→0.

把(12)和(22)代入(11)，并简化之得

‖xn+1-z‖2=(1-αn)‖xn-z‖2+

2αnωn+M2

在引理3中取an=‖xn-z‖2,λn=αn,

bn=2αnωn,cn=M2，易知引理2中的所有条件均被满足，从而得知xn→z(n→∞).

结论证毕.

在定理1中取βn=1,∀n≥0则可得下面的结果.

D→D是一致L-Lipschitz非扩张映射.

设F(T)非空，再设{αn},{βn},{δn},{σn}是[0,1]中的序列，αn+δn=1,βn+σn=1,且满足下面的条件：

对给定的x∈D及对n≥1，定义压缩映射Sn:

D→D如下

Sn(z)=(1-dn)x+dnTnz,

其中

(23)

设zn是Sn的唯一不动点，即zn满足：

zn=Sn(zn)=(1-dn)x+dnTnzn,n≥1

(24)

如果下面的条件满足：

(1){zn}强收敛于某一z∈F(T);

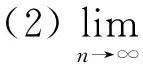
则由定理2迭代序列{xn}强收敛于z∈F(T).

定义压缩映射St:D→D如下

St(z)=(1-t)x+tT(z),z∈D

(25)

其中0

证明 因T是非扩张的，故T是具常数列{1}的渐近非扩张映射，在(11)到(18)及(21)式中取L=1,t→1-,zm=zt,Tmzm=Tzt，仿效定理1的证明，类似可证定理3的结论成立，证毕.

2 结束语

[1] Tian Y X, Chang X X, Huang J L.On the approximation problem of common fixed points for a finite-family of non-self asymptotically quasi-nonexpansive-typemappings in Banach spaces. Computers & Mathematics with Applications, 2007，53:1847-1853.

[2] MOUDAFI A. Viscosity Approximation Methods for Fixed Points Problems[J]. J Math Anal Appl, 2000, 241(1): 46-55.

[3] Chang S S.Some problems and results in the study of nonlinear analysisi[J].Nonlinear Anal TMA,1997,30(7):4197-4208.

[4] Liu L S.Ishikawa and Mann iterative process with errors for expansive mapping in Banach spces[J].J Math Anal Appl,1995,194:114-125.

[5] Deimling K.Nonlinear Functional Analysis [M].Beilin, Springer Verlag,1985.

[6] 张石生． Banach空间中渐近非扩张映象不动点的迭代逼近题[J]．应用数学学报，2001，24(2)：236-241.

[7] 杨莉，张石生．渐近非扩张映象具误差的迭代序列的收敛性[J]．数学的实践与认识，2006，36(12)：261-268.

(责任编辑：于达)

Convergence of Reich-Takahashi Iterative Sequence

Liu Hui

(Heilongjiang University of Finance and Economics)

The proof of the convergence of Reich-Takahashi iterative sequence to the fixed point of the uniformly L-Lipschitz non-expansive mappingsTis given in this paper, which the mappingsSn(z)=(1-dn)x+dnTnzconverge to.

Banach space；Reich-Takahashi iterative sequence；Gteaux Differentiable

2016-01-23

O177

A

1000-5617(2016)02-0069-04