一种新的非线性共轭梯度法及其全局收敛性

刘峥嵘

(1.广西大学；2.广东石油化工学院)



一种新的非线性共轭梯度法及其全局收敛性

刘峥嵘1,2

(1.广西大学；2.广东石油化工学院)

根据陈继宏等人给出的βk的新取值，结合田亚娟等提出的线搜索方法，提出一种新的混合算法，并对其充分下降性和收敛性做出了证明．

共轭梯度法;全局收敛;下降性

1 新的共轭梯度法及其公式

陈继红、焦宝聪等人在文献[1]中提出了一个新的共轭参数：

(1)

随后Yu Gaohang等人在文献[2]中对上述参数进行推广得到：

(2)

基于上述参数的共轭梯度法被证明了具有很好的全局收敛性，并在数值验算中表现较好．受上述共轭参数取值的启发，本章得到一个新的共轭参数公式：

(3)

这里μ∈(1,+∞)，此方法简称为方法(3)．

另外，该文采取田亚娟等在文献[3]中提出的，由Wolfe线搜索推广而来的新搜索方法：

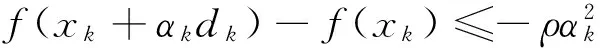
(4)

(5)

这里0<ρ≤σ1<1,σ2≥0,并满足σ1+σ2≤1．

以下给出该文的算法：

算法1.1

步骤1 设置初始值d0=-g0,k:=0；

步骤2 判断，若gk≤ε，则算法终止；

否则利用线搜索式(4)、(5)求步长因子αk；

令xk+1=xk+αkdk；

2 新算法的全局收敛性

为方便叙述，假设gk≠0对所有的k>0成立，否则迭代已经在稳定点上，同时假设目标函数满足：

(A) 目标函数f (x)在水平集L2={x∈Rn|f(x)≤f(x0)}上有界；

(B) 在水平集L2={x∈Rn|f(x)≤f(x0)}的一个邻域U内，目标函数f (x)连续可微，且其导数g(x)满足Lipschitz条件，即存在L为常数使下式成立：

‖g(x)-g(y)‖≤L‖x-y‖

引理2．1 设目标函数f (x)满足假设条件(A)、(B)，方法(3)在线搜索条件(4)、(5)下具有充分下降性．

-c‖gk‖2．

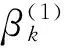
证明 由目标函数满足假设条件(A)可知{f (x)}有界，又由式(4)可得fk+1≤fk故

{f (x)}收敛．

由式(5)及假设条件(B)可得：

(7)

则结合式(4)可得：

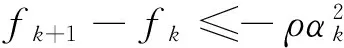
(8)

(9)

引理2.3 设{αi}为正项级数，若有

(10)

其中k为整数，c为常数，l>0．

另外，若目标函数f (x)满足假设条件(A)、(B)，则由方法(3)产生的迭代序列包含于水平集L2中；又因{f (x)}为下降序列，故存在一常数h使得

(11)

同时对k>0，也存在常数M使下式成立：

‖gk‖≤M ．

(12)

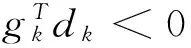
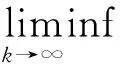
上式左右同时除以‖gk‖4，得

(13)

因此结合引理2.3，有

+∞,

即

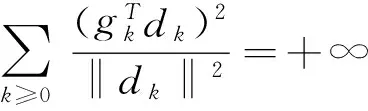
这与引理2.2矛盾，因而假设不成立，定理得证．

[1] 陈继红,焦宝聪.一种新的非线性共轭梯度法的全局收敛性[J].首都师范大学学报:自然科学版, 2006,27(3):1-4.

[2] Yu Gaohang, Zhao Yanlin, Wei Zengxin. A descent nonlinear conjugate gradient method for large-scale unconstrained optimization[J].Applied mathematics and computation, 2007,187:636-643.

[3] 田亚娟,马昌凤.一种新的共轭梯度法的全局收敛性[J].广西科学,2006(4):279-281.

(责任编辑：于达)

A New Nonlinear Conjugate Gradient Method and its Global Convergence

Liu Zhengrong1,2

(1.Guangxi University;2. Guangdong University of Petrochemical Technology)

According to the new valuesβkgiven by Chen Jihong and others, a new hybrid algorithm is proposed, which is based on the line search method proposed by Tian Yajuan et al. The descent property and global convergence of the hybrid algorithm are proved.

Conjugate gradient method; Global convergence; Descent property

2016-01-22

O221.2

A

1000-5617(2016)02-0050-02