基于全正基的三次均匀B样条曲线的扩展

严兰兰， 韩旭里

(1. 东华理工大学理学院，江西 南昌 330013；2. 中南大学数学与统计学院，湖南 长沙 410083)

基于全正基的三次均匀B样条曲线的扩展

严兰兰1,2， 韩旭里2

(1. 东华理工大学理学院，江西 南昌 330013；2. 中南大学数学与统计学院，湖南 长沙 410083)

为了构造具有保形性的三次均匀B样条扩展曲线，首先运用拟扩展切比雪夫空间的理论框架证明现有文献中的三次Bézier曲线的扩展基，简称λ-Bézier基，恰为相应空间的规范B基。然后用λ-Bézier基的线性组合来表示三次均匀B样条曲线的扩展基，根据预设的曲线性质反推扩展基的性质，进而求出线性组合的系数。扩展基可表示成λ-Bézier基与一个转换矩阵的乘积，证明了转换矩阵的全正性及扩展基的全正性。由扩展基定义了基于3点分段的曲线，分析了曲线的性质，扩展基的全正性决定了曲线可以较好的模拟控制多边形的形态。简要介绍了由扩展基定义的基于16点分片的曲面。

曲线设计；保形性；全正基；形状参数

在计算机辅助几何设计(computer aided geometric design，CAGD)中，Bézier方法与B样条方法是描述自由曲线曲面的主流方法，其满足形状数学描述的诸多要求，如唯一性、几何不变性、几何直观等。但任何事物都不可能尽善尽美，Bézier和B样条方法也不例外，因此不断有文献对两种方法进行改进。目前对Bézier、B样条方法的改进主要集中在2个方面：①通过在基函数中引入参数，来增强Bézier、B样条方法的形状调整能力，如文献[1-5]中具备Bézier方法的端点插值、端边相切等性质的曲线，及文献[6-8]中具备B样条方法的局部性、自动光滑性等特征的曲线，均可在不改变控制顶点的情况下，通过调整参数值来改变曲线形状。②通过在非多项式空间，如三角[9-13]、双曲函数空间[14-16]中构造合适的基函数，使相应曲线在具备Bézier[9-11,13]或B样条[11-13,15]方法类似性质的同时，还能表示一种或多种圆锥曲线和超越曲线。

上述文献中的方法不仅具备Bézier或B样条方法的基本性质，如几何不变性、对称性、凸包性等，而且还具备形状可调性，或者能精确表示工程中常用的特殊曲线，但多数文献并未讨论其构造的曲线是否具有变差缩减(variation dim inishing，VD)性。VD性是Bézier、B样条曲线的重要性质之一，具有VD性的曲线一定具备保凸性，具有全正性的调配函数定义的曲线一定具有VD性，因此是否具有全正性是衡量一组调配函数是否适合于保形设计的标准之一。

三次Bézier、B样条曲线结构简单又不失灵活度，在工程中使用最为广泛，在文献中也讨论最多。文献[1]给出了一组含参数的三次 Bézier曲线的扩展基，本文证明了该扩展基是相应空间上的最优规范全正基，因此由之定义的曲线具有变差缩减性、保凸性，能最好地模拟控制多边形的形态。但该曲线不具备局部性和自动光滑性，为此，本文在这组最优规范全正基的基础上乘以全正的转换矩阵，得到了一组含参数的规范全正基，由之定义了基于3点分段的曲线。该曲线包含三次均匀B样条曲线为特例，具备局部控制性、变差缩减性与保凸性。对于等距节点，该曲线一般情况下 C2连续，取特殊参数可达FC3连续。

1 预备知识

用I表示任意给定的闭区间[a,b]，下面给出完备扩展切比雪夫(extended completed Chebyshev，ECC)空间和拟扩展切比雪夫(quasi extended Chebyshev，QEC)空间的定义[16]。

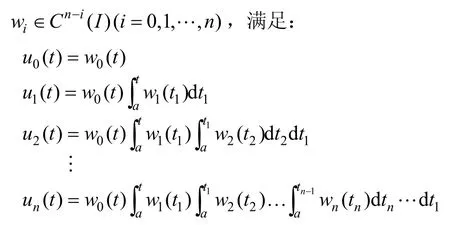
定义1. (ECC空间). 若存在n+1个正的权函数则称空间 (u0,u1,…,un)为n+1维的ECC空间。

n+1维函数空间(u0,u1,… ,un) ⊂Cn(I )为闭区间I上的一个ECC空间的充要条件是：对于任意的整数k (0≤k≤n)，子空间(u0,u1,… ,uk)中的任意一个线性组合在I上至多只有k个零点(包括重根)。

定 义 2. (QEC 空 间 ). 若 空 间(u,u ,…,u )⊂Cn-1(I)中的任意一个线性组合在闭0 1 n区间I上至多只有n个零点(作为空间Cn-1(I)的元素，重根至多算到n重)，则称 (u0,u1,…,un)为I上的一个QEC空间。

定义 3. (全正基). 称基函数(u0,u1,… ,un)为I上的全正基，若对于任意的节点序列a≤t0＜t1＜…＜tn≤b ， 基 函 数 的 配 置 矩 阵(uj(ti))0≤i,j≤n为全正矩阵，即配置矩阵的所有子式非负。

对于具有全正基的函数空间而言，其中的最优规范全正基(即规范B基)是唯一的。在规范B基的基础上乘以全正的转换矩阵，可以生成其余的全正基。在所有全正基中，规范B基且具有最优的保形性，即由之定义的曲线能够最好地模拟控制多边形的形态，例如当控制多边形为凸时，生成的曲线也为凸。

2 三次Bézier曲线的扩展基

文献[1]构造了一组含参数的四次多项式函数，以三次Bernstein基为特例，由之定义的曲线具有与三次Bézier曲线相同的结构和类似的性质。

定义4. 对t∈[0,1]， λ∈[- 3,1]，称关于t的多项式：

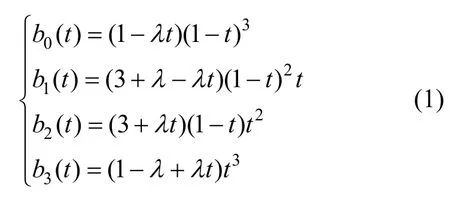
为带参数λ的三次 Bézier曲线的扩展基，简称λ-Bézier基。

由式(1)知λ-Bézier基具有规范性并且线性无关，b1(t)和b2(t)可改写成：

接下来运用拟扩展函数空间的理论框架证明：对于任意的 λ∈(-3 ,1]，空间Sλ均适用于构造曲线。为此，先证明Sλ的微分空间DSλ=:span为 [0,1]上的3维QEC空间。

定理1. 对于任意的 λ∈(- 3,1]，DSλ为[0,1]上的一个3维QEC空间。

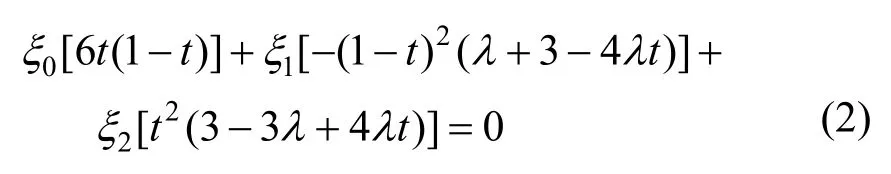
在式(2)中令t=0得ξ1=0，令t=1得ξ2=0，进而ξ0= 0，故DSλ为[0,1]上的3维函数空间。

现在证明DSλ为（0, 1）上的3维ECC空间。对于任意的，令：

易知u(t)＞0，v(t)＞0。直接计算可得：

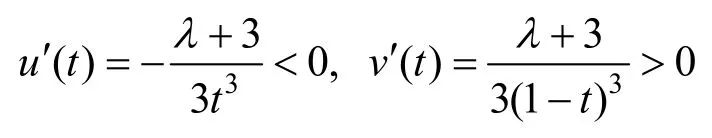
因此u(t)和v(t)的朗斯基行列式：

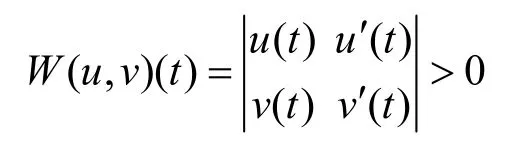
对于t∈[a,b]，定义权函数：

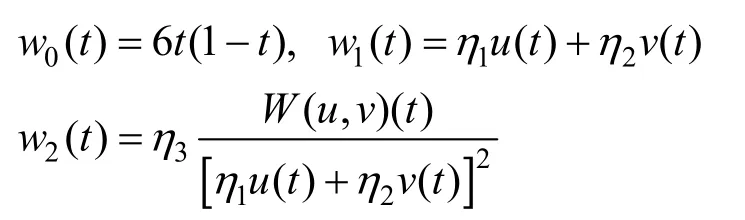
其中，θi＞ 0 (i = 1,2,3)，显然 wi(t)(i = 0,1,2)为[a,b] 上C∞且正的有界函数。考虑ECC空间：

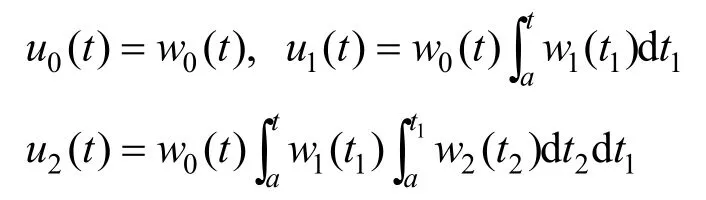
知 ui(t)(i = 0,1,2)为 函 数 6t(1-t) ，的线性组合，因此DSλ为[a,b]上的ECC空间。由于[a,b]为(0,1)上的任意子区间，故DSλ为(0,1)上的ECC空间。

为进一步证明DSλ为[0,1]上的 QEC空间，需先证明DSλ的任意一个非零元在[0,1]上至多只有两个零点(注意重根至多算到二重)。考虑DSλ中的任意一个非零函数：

由于DSλ为(0,1)上的ECC空间，故F(t)在(0,1)上至多只有两个零点。

假设t=0为F(t)的零点，则C1=0。在此情形下，若C2=0，则t=0和t=1均为F(t)的单根。若C0= 0，则t=0至多为F(t)的二重根(重根至多算到二重)。若 C0C2＞ 0，则t=0为F(t)的单根，且F(t)在区间(0,1]上恒正或恒负。若 C0C2＜ 0，则t= 0为F(t)的单根且t=1不是F(t)的根。此外，考虑函数：

由 于 G(t) 在 [0,1] 上 连 续 ， 且G(0)G (1) =6(3 +λ)C0C2＜0，故由零点定理可知G(t)在(0,1)内至少存在一个零点。又当λ≠0时，G(t)是关于t的二次函数，假设G(t)在(0,1)内有两个零点t1和t2，则，故G (0)G (1) ＞ 0，矛盾。当λ=0时，G(t)退化为一次函数，只有一个零点。综上可知G(t)在(0,1)内恰有一个零点，进而 F(t) =tG(t)(此时C1=0)在(0,1)内也恰有一个零点。上述分析表明当t=0为F(t)的零点时，F(t)在[0,1]上至多有两个零点。同理当t=1 是F(t)的零点时，F(t)在[0,1]上也至多只有两个零点。 证毕。

注释1. 由于DSλ为[0,1]上的3维QEC空间，故由文献[17]中的定理3.1可知，空间Sλ中存在开花，这表明对于任意的 λ∈(-3 ,1]，空间Sλ均适用于构造曲线。此外，由文献[17]中的定理2.13和定理2.18，可知Sλ在[0,1]上具有规范B基。

注释2. 当λ=-3时，F(t)在[0,1]上可能存在3个不同的零点。例如当C0=0，C1=C2=1时，F(t)具有零点0、、1。这意味着当λ=-3时，DSλ不是[0,1]上的QEC空间。因此从开花的角度讲，当λ=-3时，空间Sλ不适合于曲线设计。

定理2. 对于任意的 λ∈(- 3,1]，由式(1)定义的λ-Bézier基具有最优规范全正性。

证明：对任意的 λ∈(-3 ,1]，由式(1)容易验证bi(t)(i = 0,1,2,3)具有如下端点性质：

(1) 对于i=0,3，bi(0)=1且 bi(t)在t=1处有三重根(重根至多算三重)；

(2) 对于i=1,2， bi(t)在t=0处恰有i重根，在t=1处恰有3-i重根。

此外， bi(t)(i = 0,1,2,3)在(0,1)内是严格正的，故由文献[17]中的定理2.18可知，λ-Bézier基恰为Sλ中的规范B基。 证毕。

3 三次均匀B样条曲线的扩展基

3.1 扩展基的构造

将基于λ-Bézier基构造带形状参数的三次均匀B样条扩展基。令：

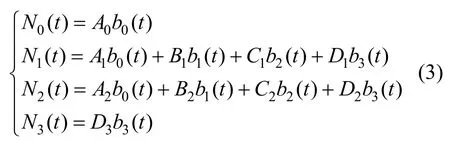
其中，bi(t)(i = 0,1,2,3)为λ-Bézier基，A·、B·、C·、D·为待定系数。

为确定待定系数的值，先预设由式(3)定义的结构与三次均匀 B样条曲线相同的分段曲线具有对称性、凸包性、 C2连续性，由此反推出由式(3)给出的函数组必须具有：

(1) 对称性：

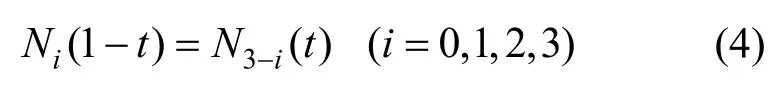
(2) 规范性：

(3) 端点特征：

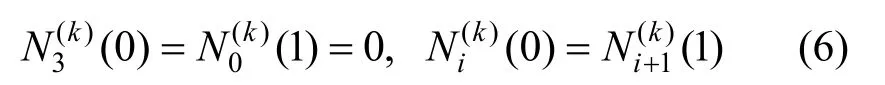
其中， k= 0,1,2,i=0,1,2。

由式(3)～(6)可计算出：

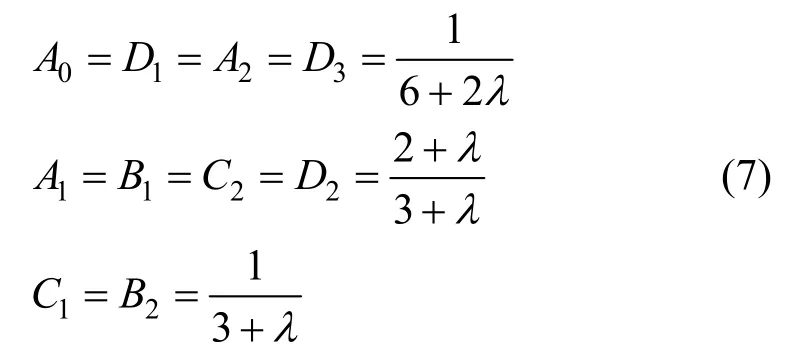
由式(3)、(7)可得：

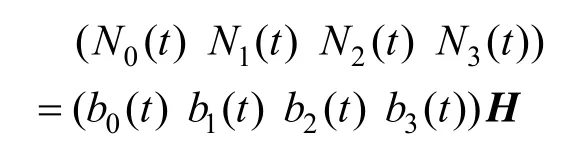
其中，转换矩阵为：

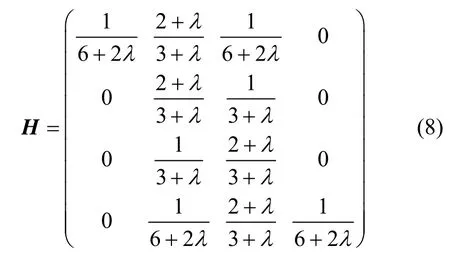
下面讨论矩阵H的全正性。

定理3. 当 λ∈(-1 ,1]时，由式(8)给出的矩阵H为非奇异随机全正矩阵。

证明：易知矩阵H的各行元素之和全为1，且当 λ∈(- 1,1]时，H的所有元素非负，故H为随机矩阵。由式(8)可知，其中，

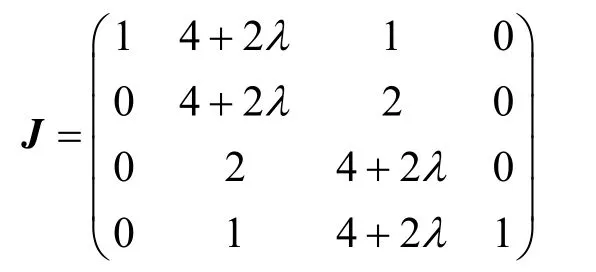
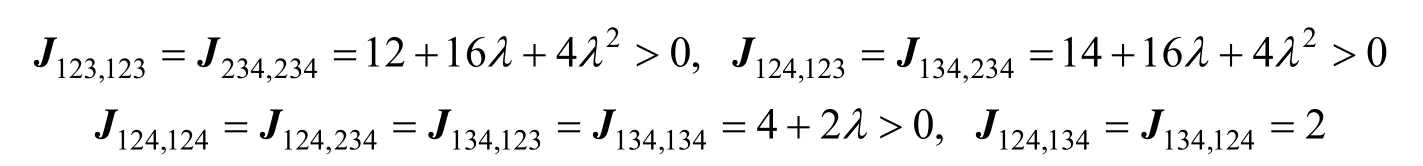
其余全为0，其中Jij,kl表示由J的i与j行，k与l 列形成的子式。J的三阶子式分别为：其余全为0，其中 Jijk,lmn表示由J的i,j,k行，l,m,n列形成的子式。故J为非奇异全正矩阵，从而H为非奇异随机全正矩阵。 证毕。

由 bi(t)(i = 0,1,2,3)的最优规范全正性，以及转换矩阵H的非奇异随机全正性可知，Ni(t)(i = 0,1,2,3)形成函数空间Sλ中的一组全正基。

定义5. 对t∈[0,1]， λ∈(-1 ,1]，称关于t的多项式：

为三次均匀B样条扩展基，简称λ-B样条基。

3.2 扩展基的性质

由上面的分析可得λ-B样条基的下列性质:

(1) 退化性。当λ=0时，λ-B样条基即三次均匀B样条基。

(2) 非负性。当 λ∈(-1 ,1]时，对任意的t∈[0,1]，有 Ni(t) ≥ 0(i =0,1,2,3)。

(4) 对 称 性 。 Ni(1 -t) = N3-i(t )， 其 中i= 0,1,2,3。

(5) 端点性质。对任意的 λ∈(-1 ,1]，有：

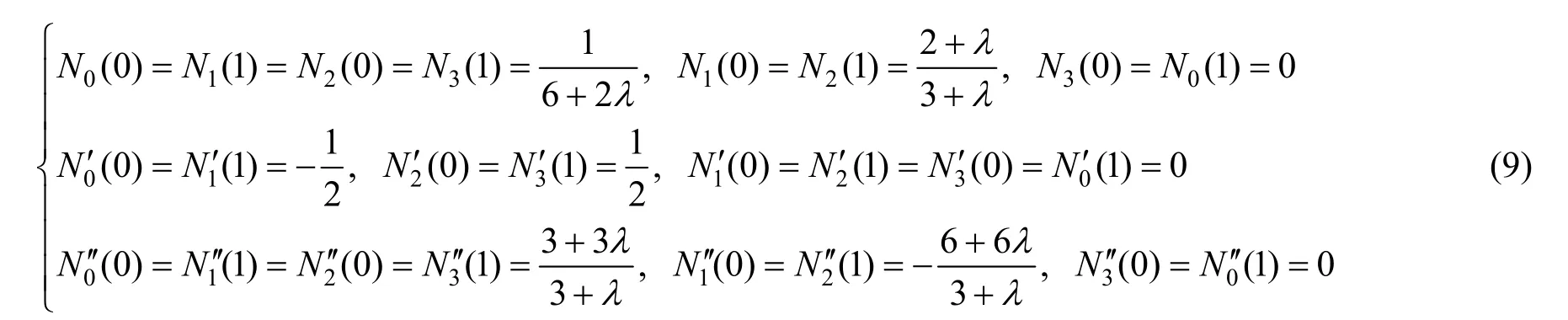
当λ=1时，有：

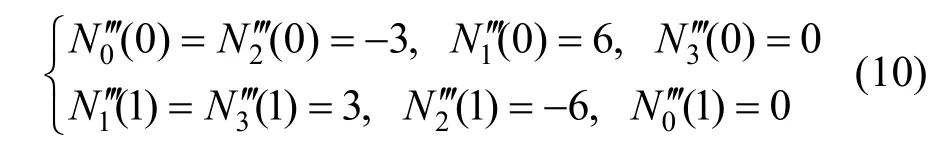
(6) 全正性。对于任意的 λ∈(- 1,1]，λ-B样条基为函数空间Sλ中的规范全正基。

4 三次均匀B样条扩展曲线

4.1 曲线及其性质

定 义 6. 给 定 控 制 顶 点P∈Rd(d =2,3;i =0,1,… ,n)， 节 点iu1＜u2＜… ＜un-1，参数 λ∈(- 1,1]，可定义n-2条如下的曲线段：

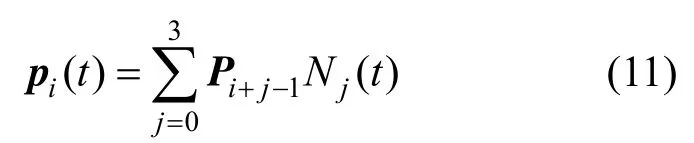
其中，t∈[0,1]，i =1,2,… ,n -2， Nj(t) ( j=0,1,2,3) 为λ-B样条基，所有曲线段构成一条含一个形状参数的分段组合曲线：

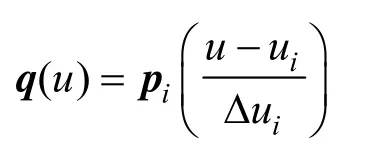
其中， u∈[ui,ui+ 1]⊂[u1,un -1]， Δui= ui+ 1-ui，i=1,2,… ,n -2，称q (u)为λ-B曲线。

由λ-B样条基的性质，可得λ-B曲线的下列性质：

(1) 几何不变性与仿射不变性。λ-B样条基具有规范性，故λ-B曲线的形状与坐标系的选取无关；欲获得经仿射变换后的曲线，只需对控制多边形执行相同变换再定义曲线。

(2) 对称性。λ-B样条基具有对称性，故当不改变λ的值时，由控制多边形 P0P1… Pn和PnPn-1…P0定义的λ-B曲线形状相同，只是方向相反。

(3) 局部控制性。由于λ-B曲线结构与三次B样条曲线相同，故改变一个控制顶点，至多只有4 条λ-B曲线段的形状会发生改变。

(4) 形状可调性。由于λ-B样条基中含参数λ，改变λ的值，参与计算的样条基发生改变，因此即使控制顶点和节点固定，相应曲线的形状依然会发生改变。

(5) 连续性。由式(9)、(11)，容易推出：

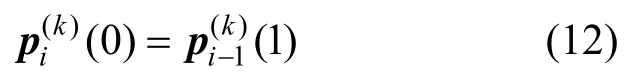
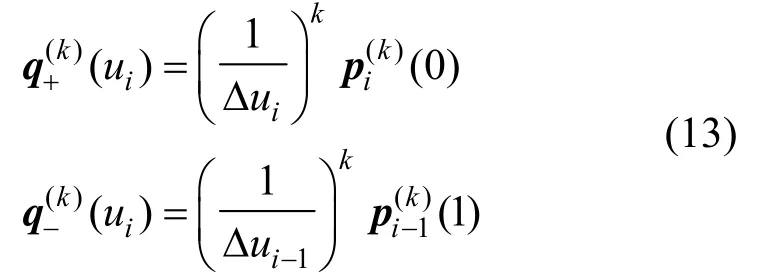
结合式(12)、(13)有：

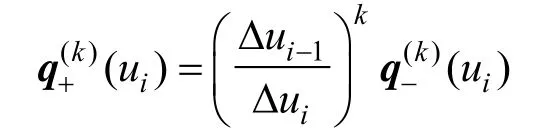
其中，k = 0,1,2，这表明λ-B曲线一般情况下 G2连续，当节点等距时 C2连续。当λ=1时，由式(9)～(11)可得：

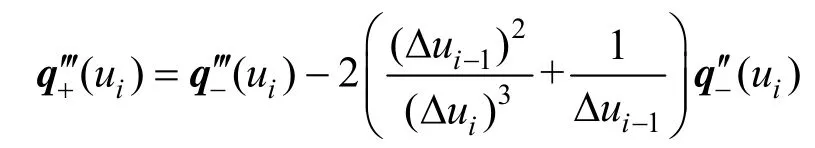
这表明λ-B曲线3FC连续。

(6) 凸包性。λ-B样条基具有非负性与规范性，故λ-B曲线段 pi(t )位于控制顶点 Pi- 1,Pi,Pi+ 1,Pi +2的凸包Hi内，整条λ-B曲线q(u)位于所有凸包Hi的并集内。

(7) VD性。λ-B样条基是规范全正基，故λ-B曲线具有VD性，这意味着λ-B曲线适用于曲线设计。

(8) 保凸性。由 VD性可知，当控制多边形为凸时，直线与λ-B曲线的交点个数不超过两个，因为直线与控制多边形的交点个数至多为两个，因此λ-B曲线能够保持控制多边形的凸性。

4.2 曲线设计

为了用λ-B曲线设计出满意的形状，首先要知道参数λ对曲线形状的影响。

由式(9)、(11)可得：

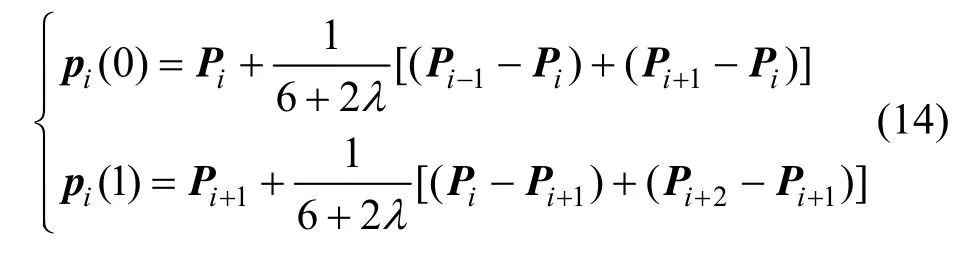
由式(14)可知：第 i条曲线段的起点位于以边PiPi-1和PiPi+1为邻边形成的平行四边形的对角线(起点为 Pi)上，起点与 Pi的距离为该对角线长度的倍。对曲线段的终点也有类似结论。因此λ值越大，曲线段的起点越接近点 Pi，终点越接近点Pi+1，所以增加λ值的作用是将曲线段拉向中间的控制边，见图1。

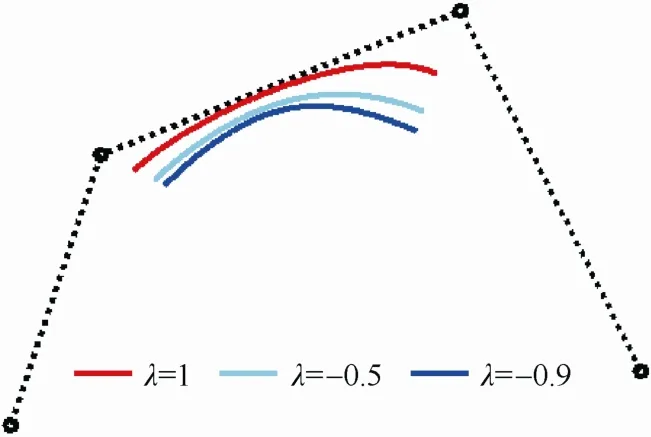
图1 参数λ的作用

从式(14)还可以看出，若λ-B曲线的控制顶点满足条件：

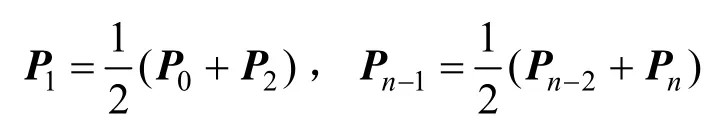
则无论λ取何值，均有 q (u1)=P1， q (un-1)= Pn-1。因此要想使λ-B曲线经过控制多边形 P0P1… Pn的首末顶点，只需增加辅助点 P-1= 2P0-P1，Pn+1=2Pn-Pn-1，再由控制多边形 P-1P0…Pn+1定义曲线即可(如图2(a)所示)。若原始控制多边形封闭，即P0=Pn，则该方法将产生一条封闭曲线，但一般情况下该曲线在闭合点处仅位置连续，并不光滑。若希望由封闭的控制多边形生成封闭且光滑的曲线，只需增加辅助点 Pn+1=P1， Pn+ 2=P2，然后由多边形 P0P1…Pn+2定义曲线即可(如图 2(b)所示)。图2中圆点为初始控制点，方形点为辅助点。

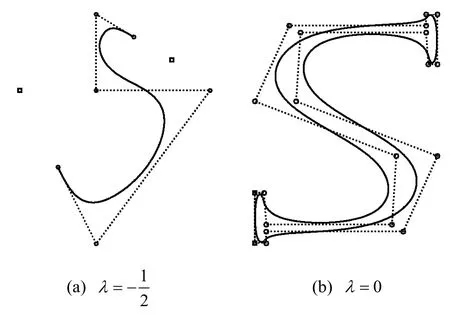
图2 λ-B曲线

4.3 曲线的保形性

现有文献在构造形状可调曲线时，形状参数的取值范围通常是由基函数的非负性来给出的，这样得到的曲线虽然具备凸包性，但不一定具备保凸性，因此不能较好地保持控制多边形的形状，无法设计出满意的结果。

对于λ-B曲线而言，当 λ∈[- 2,1]时，曲线具有凸包性，由前面分析可知，当 λ∈(-1 ,1]时，曲线一定具有保凸性。图2中的形状在字母设计中较常用，针对图2中的控制点分别取 λ=- 1.2,- 1.5,-2，得到的曲线如图3所示，可以看出，如果像多数文献那样来构造形状可调曲线，只能保证曲线的形状调整能力，而无法保证形状调整质量，从而难以应用于工程实际。

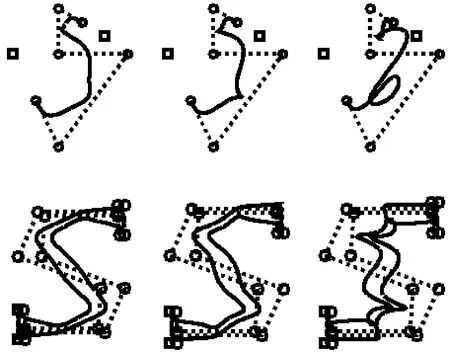
图3 不保形的曲线

5 三次均匀B样条扩展曲面

利用张量积方法可将λ-B曲线推广至四边域曲面，从而得到三次均匀B样条扩展曲面。

定 义 7. 给 定 控 制 顶 点Pij∈R3(i = 0,1,… ,m; j =0,1,… ,n)， 节 点u1＜u2＜… ＜um-1与v1＜v2＜ … ＜vn-1，以及参数λ1,λ2∈(-1 ,1]，可以定义(m - 2)×(n - 2)张曲面片，即：

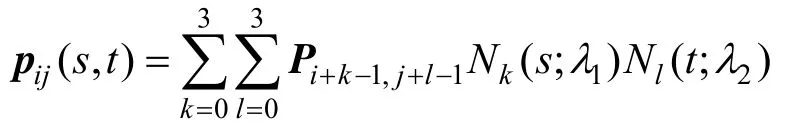
其中，s,t ∈ [0,1]，i =1,2,… ,m -2， j=1,2,…,n -2，Nk(s;λ1)和 Nl(t;λ2)分别是参数为 λ1和 λ2的λ-B样条基，所有曲面片构成一张含两个形状参数的分片组合曲面：

λ-B曲面具有与λ-B曲线类似的性质。例如：在一般情况下，λ-B曲面关于u、v方向均 G2连续；当λ1=λ2 =1时，关于u、v方向均 FC3连续。

图4所示为由相同控制网格和不同参数定义的λ-B曲面。

6 结 束 语

目前关于形状可调曲线的文献非常丰富，大量与Bézier或B样条曲线性质类似的可调曲线被提出。这些曲线克服了传统Bézier、B样条曲线相对于控制多边形形状固定的不足，但对于其是否像Bézier、B样条曲线一样，具有VD性、保形性，从而适用于曲线设计的讨论却很少，因此从全正性的角度来检验已有的扩展曲线，以及寻找新的基于全正基的扩展曲线是有意义的。本文正是基于这种思想的一次尝试，一方面给出了文献[1]中的扩展基全正时的参数取值范围，另一方面给出了一类新的具有保形性的三次均匀B样条扩展曲线。

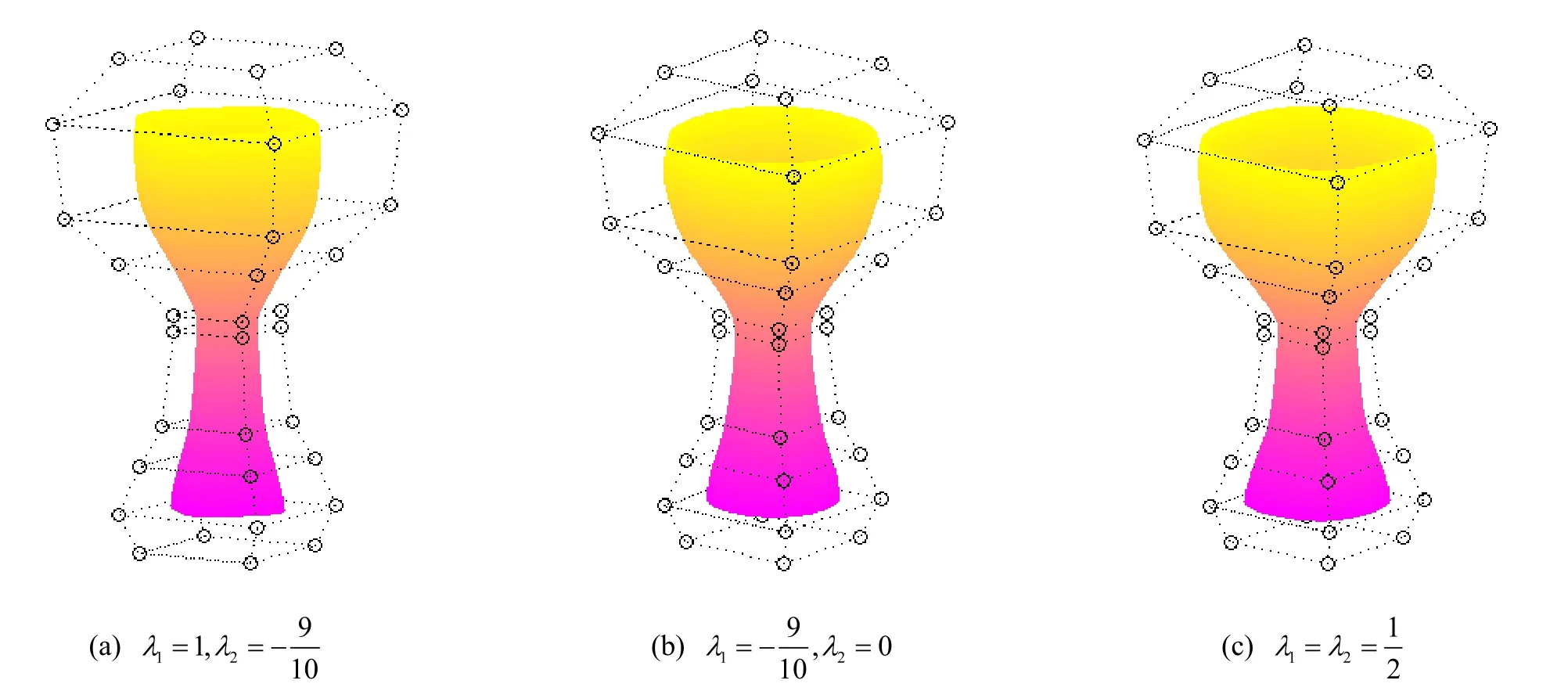
图4 λ-B曲面

[1] 吴晓勤, 韩旭里. 三次 Bézier曲线的扩展[J]. 工程图学学报, 2005, 26(6): 98-102.

[2] 仇 茹, 杭后俊, 潘俊超. 带三参数的类四次 Bézier曲线及其应用研究[J]. 计算机工程与应用, 2014, 50(20): 158-162.

[3] Wang W T, Wang G Z. Bézier curves with shape parameter [J]. Journal of Zhejiang University SCIENCE A, 2005, 6A(6): 497-501.

[4] Chen J, Wang G J. A new type of the generalized Bezier curves [J]. Applied Mathematics-A Journal of Chinese Universities, 2011, 26(1): 47-56.

[5] Qin X Q, Hu G, Zhang N J, et al. A novel extension to the polynomial basis functions describing Bezier curves and surfaces of degree n with multiple shape parameters [J]. Applied Mathematics and Computation, 2013, 223(10): 1-16.

[6] 韩旭里, 刘圣军. 三次均匀B样条曲线的扩展[J]. 计算机辅助设计与图形学学报, 2003, 15(5): 576-578.

[7] 王树勋, 叶正麟, 陈作平. 带最多独立形状参数的三阶三次均匀B样条曲线[J]. 计算机工程与应用, 2010, 46(15): 142-145.

[8] Xu G, Wang G Z. Extended cubic uniform B-spline and α-B-spline [J]. Acta Automatica Sinica, 2008, 34(8): 980-984.

[9] 耿紫星, 张贵仓. Bézier曲线的三角扩展[J]. 计算机工程与应用, 2008, 44(26): 59-62.

[10] Chen Q Y, Wang G Z. A class of Bézier-like curves [J]. Computer Aided Geometric Design, 2003, 20(1): 29-39.

[11] Han X L, Zhu Y P. Curve construction based on five trigonometric blending functions [J]. BIT Numerical Mathematics, 2012, 52(4): 953-979.

[12] Su B Y, Tan J Q. A family of quasi-cubic blended splines and applications [J]. Journal of Zhejiang University SCIENCE A, 2006, 7(9): 1550-1560.

[13] 尹池江, 檀结庆. 带多形状参数的三角多项式均匀 B样条曲线曲面[J]. 计算机辅助设计与图形学学报, 2011, 23(7): 1131-1138.

[14] 张锦秀, 檀结庆. 代数双曲 Bézier曲线的扩展[J]. 工程图学学报, 2011, 32(1): 31-38.

[15] 邬弘毅, 左 华. 多形状参数的二次非均匀双曲B样条曲线[J]. 计算机辅助设计与图形学学报, 2007, 19(7): 876-883.

[16] Han X L, Zhu Y P. Total positivity of the cubic trigonometric Bézier basis [J]. Journal of Applied Mathematics, 2014, (3): 1-5.

[17] Marie-Laurence. Which space for design [J]. Numerische Mathematik, 2008, 110(3): 357-392.

The Extended Cubic Uniform B-Sp line Curve Based on Totally Positive Basis

Yan Lanlan1,2, Han Xuli2

(1. School of Science, East China University of Technology, Nanchang Jiangxi 330013, China; 2. School of Mathematics and Statistics, Central South University, Changsha Hunan 410083, China)

This paper aims to construct a shape-preserving extended cubic uniform B-spline curve. Firstly, within the theoretical framework of quasi extended Chebyshev space, we prove that the existing extended basis of the cubic Bézier curve, λ-Bézier basis for short, is the normalized B-basis of the corresponding space. Then we use the linear combination of the λ-Bézier basis to express the extended basis of the cubic uniform B-spline curve. According to the preset properties of the curve, we deduce the properties of the extended basis, and then determ ine the coefficients of the linear combination. The extended basis can be represented as the product of the λ-Bézier basis and a conversion matrix. We prove the totally positive property of the matrix and the extended basis. By using this basis, we define a curve based on 3-point piecew ise scheme and analyze its properties. The totally positive property makes the curve can simulate the shape of the control polygon. The surface based on 16-point piecew ise scheme is briefly introduced.

curve design; shape preserving property; totally positive basis; shape parameter

TP 391.72

10.11996/JG.j.2095-302X.2016030329

A

2095-302X(2016)03-0329-08

2015-10-30；定稿日期：2015-11-27

国家自然科学基金项目(11261003，11271376，60970097)；江西省教育厅项目(GJJ14493)；江西省自然科学基金项目(20161BAB211028)

严兰兰(1982–)，女，湖北浠水人，副教授，博士研究生。主要研究方向为计算机辅助几何设计。E-mail：yxh821011@aliyun.com