基于NSCT的自适应乘性水印局部最优非线性盲检测算法

叶建兵， 张文彬

(南京理工大学泰州科技学院，江苏 泰州 225300)

基于NSCT的自适应乘性水印局部最优非线性盲检测算法

叶建兵， 张文彬

(南京理工大学泰州科技学院，江苏 泰州 225300)

图像水印算法研究是多媒体技术领域中的重要议题。比较并结合当前两类主流的图像水印算法，提出了一种基于非下采样 Contourlet变换的自适应乘性水印算法。借鉴 Barni的“pixel-w ise masking”模型和冗余小波域掩盖效应建模的做法，建立非下采样Contourlet变换域掩盖效应计算模型。用广义高斯分布模型和Cauchy分布模型描述非下采样Contourlet变换系数的统计特性，将水印的检测问题表述为一个复合假设检验。通过理论推导分别建立了乘性水印的两种局部最优非线性盲检测器及检测门限的自适应确定方法。实验结果表明，非下采样Contourlet变换域掩盖效应计算模型使得水印嵌入算法具有良好的视觉不可见性，两种检测器在无原始图像和自适应嵌入强度系数参与检测的情况下均能准确地检测到水印信息的存在。实验结果同时显示，基于 Cauchy分布的盲检测器在检测效果和检测时间方面优于基于广义高斯分布的盲检测器。

非下采样Contourlet变换；广义高斯分布；对称α-稳定分布；柯西分布；自适应乘性水印；局部最优非线性检测器；盲检测器

数字水印是多媒体技术研究领域中的重要议题，用来解决版权保护等实际问题。数字水印算法的研究主要在图像的变换域中展开，是为了解决水印算法必须满足的不可感知性和鲁棒性的矛盾，即在图像的变换域中可以引入人类视觉系统(human visual system，HVS)特性，通过计算变换域系数的掩盖效应模型，在保证水印嵌入信息不可感知的前提下使得算法有更好的鲁棒性。最经典的掩盖效应计算模型是Barni等[1]在小波域中建立的“pixel-w ise masking”模型，该模型由图像压缩领域的研究成果改进而来。由于Barni模型的有效性，其一直以来受到研究者们的广泛关注，并被不断改进从而应用到 Contourlet变换(Contourlet transform，CT)以及非下采样 Contourlet变换(nonsubsampled Contourlet transform，NSCT)的视觉掩盖建模中。

文献[2]在冗余 Contourlet变换域(redundant Contourlet transform，RCT)、文献[3-4]分别在CT域中建立了变换系数的掩盖模型，将水印信息以加性方式嵌入到子带系数中，用相关检测器实现水印的检测。文献[5]则进一步考虑了 NSCT在水印算法研究中的优势，建立了相应的系数掩盖模型，水印的嵌入和检测算法与文献[1]和[3]中的方案一致(文献[3]给出的检测阈值有误)。文献[6]提出了一种 NSCT域的图像隐写算法，其中掩盖模型与文献[5]的模型完全相同(文献[6]给出的掩盖模型有一处小的错误)。

上述算法均采用了加性方案嵌入水印。CT域的乘性水印最早由文献[7]给出，该算法没有考虑变换域的视觉掩盖效应，采用广义高斯分布(generalized Gaussian distribution，GGD)描述高频方向子带系数的统计分布特性，但是分析发现其检测器实质上等同于文献[8]给出的一致最优势检测器(uniform ly most powerful detector，UMP)，检测器需要知道水印嵌入强度的准确信息，不满足盲检测的要求。该检测器的优势实质上只是相对于相关检测器而言。GGD模型在对CT子带系数的统计建模中得到了广泛应用，文献[9]的水印算法也采用了GGD模型，并在水印检测端用最大似然(maximum likelihood，M L)决策准则构建了一个最优检测器。文献[10]则用单变量和双变量的SαS作为CT子带系数的统计模型，并用Cauchy分布简化检测器的设计，同时降低计算复杂度。该检测器实质也是UMP检测器，同样需要嵌入强度的准确信息。

表 1给出了现有算法的比较分类。在已有的报道中，常用GGD及SαS建模具有高尖峰、长拖尾分布的变换系数。本文充分考虑 NSCT在水印算法研究中的优势，用上述两种分布描述系数的边缘统计特性，将水印信息以乘性方案嵌入经选择的变换系数，建立系数的视觉掩盖计算模型作为控制嵌入强度的权重因子，运用统计判决理论，设计适用于自适应乘性水印的局部最优非线性盲检测器，并给出检测门限的确定方法。

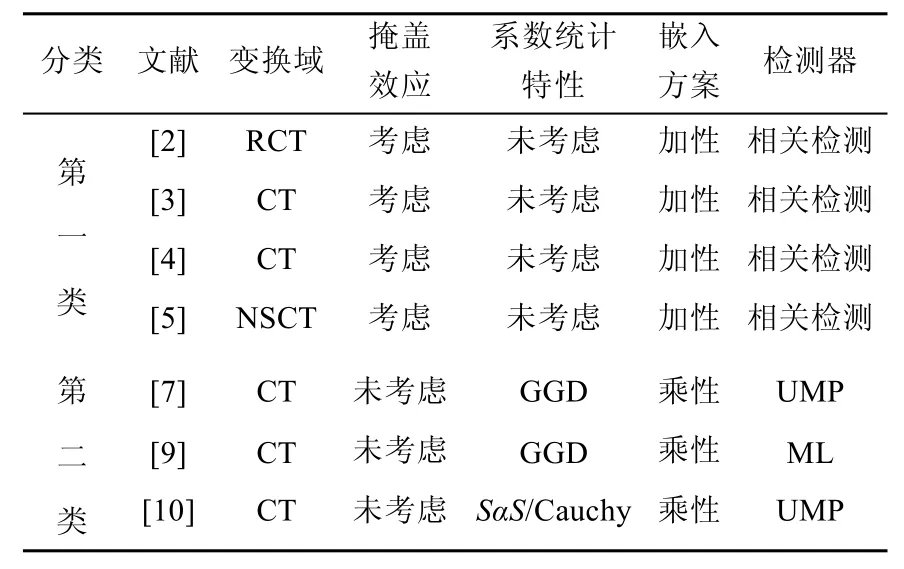
表1 现有算法的比较分类

1 CT与NSCT

文献[11]提出了一种有效的图像表示方法CT，该变换由拉普拉斯塔式(Laplacian pyram id, LP)分解和方向滤波器组(directional filter banks, DFB)分解组合实现。前者执行一次将图像分解为一个低频子带及一个高频子带，后者对高频子带进一步进行方向分解，整个过程在LP分解得到的低频子带上迭代进行，最终获得图像多分辨率、多方向性的表示，其方向性灵活，允许每个分辨率上有不同数量的方向数。

CT在LP分解和DFB分解的两步构造中都存在下采样，使其不具有平移不变性。平移不变性对图像处理至关重要，例如文献[5]认为由于正交小波变换没有平移不变性，嵌入水印的小波系数重构后在图像的边缘出现了一些伪影。

文献[12]指出CT的基函数在频域上不够局部化，方向子带之间存在频谱混叠，导致变换系数不够稀疏，系数之间有一定相关性。文献[13]则进一步分析了混叠的来源和影响，给出了解决方案。对自适应水印算法而言，频谱混叠影响了子带系数掩盖效应的估计。文献[14]提出的NSCT与CT的结构相同，利用非下采样 LP分解和非下采样DFB分解连接实现。两步构造均是非下采样，这使得 NSCT具有平移不变性，同时也不存在频谱混叠[13]，这些优势是以高度冗余性为代价的。文献[5]研究了NSCT的高冗余性在水印算法中的应用。本文选择NSCT作为水印信息的嵌入域。

2 NSCT域掩盖效应计算模型

本文在Barni模型基础上，借鉴冗余小波域掩盖效应建模的做法[15]，提出 NSCT域掩盖效应计算模型。文献[5]中NSCT将一幅图像分解为4个尺度(l=0，1，2，3)，从l=3到l=0精细尺度上方向子带数目依次为4，4，4，8，水印信息嵌入在l=0尺度上沿对角线方向的4个子带(编号为0，3，4，7)中。本文将4个尺度上的方向子带数目都分解为8，水印信息选择嵌入在l=0尺度上能量最大的方向子带中。NSCT域掩盖效应计算模型考虑了子带系数的噪声掩盖、亮度掩盖和纹理掩盖，以下简要描述该模型的实现方法。

HVS对不同尺度、不同方向(尤其45°方向)上高频子带系数中的噪声较不敏感，NSCT的l尺度、d方向子带系数对噪声的掩盖因子Θ(l,d)定义为：

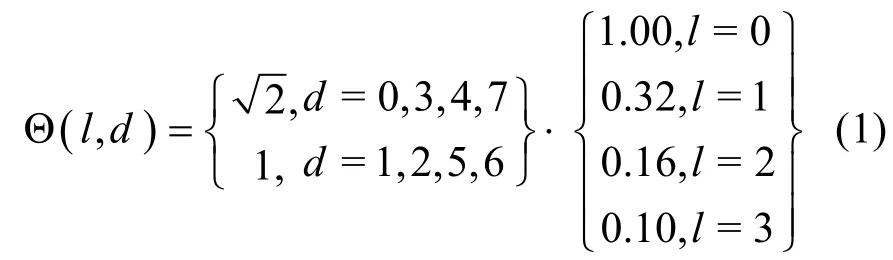
HVS对图像亮度较大或较小区域内的噪声较不敏感，l尺度上某个方向子带（i, j）位置系数的亮度掩盖因子 Λ (l ,i,j)定义为：

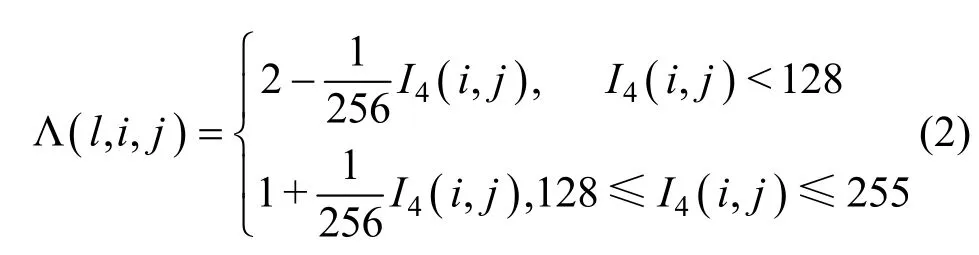
HVS对图像复杂纹理区域内的噪声较不敏感，但对边缘附近的噪声较敏感。由于 NSCT的实现过程没有下采样，系数的结构与CT不同，借鉴冗余小波域掩盖效应建模的做法[15]，l尺度上某个方向子带（i, j）位置系数的纹理掩盖因子Ξ（l,i,j）定义为：

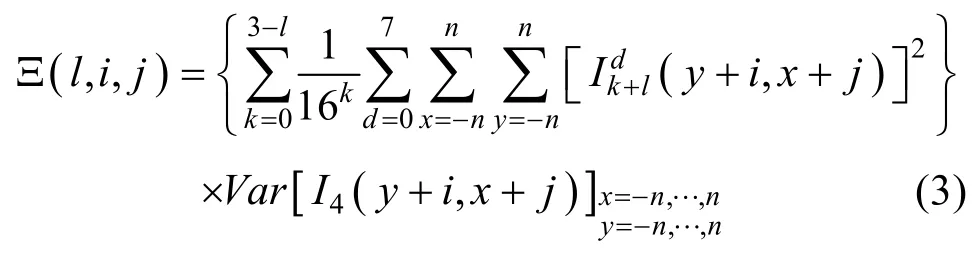
综合上述3种掩盖效应，得到NSCT的l尺度、d方向子带系数）的掩盖效应计算模型为：

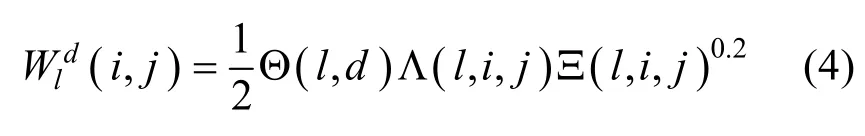
3 两种统计分布模型及其参数估计

3.1 GGD及其参数估计

零均值GGD的概率密度函数定义为[16]：

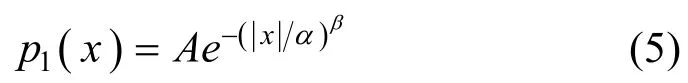
对于服从零均值 GGD 的样本X=（x1, x2,…,xL），可以证明其总体的一阶绝对矩μ1(零均值 GGD的概率密度函数为偶函数，总体一阶原点矩为零，这里用一阶绝对矩)和二阶矩μ2分别为[13]：

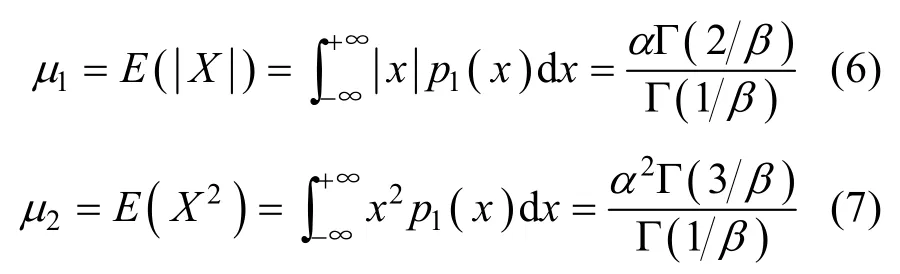
定义广义高斯参数比函数：

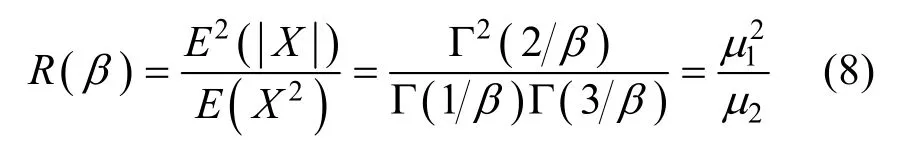
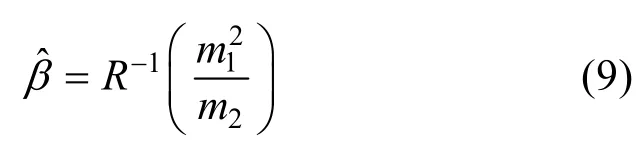
其中，R-1为R的反函数，其解析表达式很难得到，文献[13]和[17]给出的 R-1的解析表达式为：

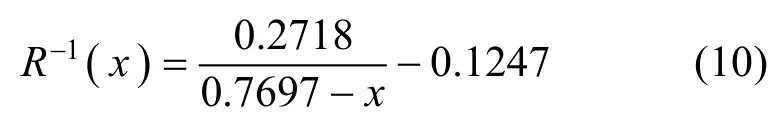
由此得到参数β的估计值精度最高，也容易实现。将式(9)代入式(6)，得到参数α的估计值为：

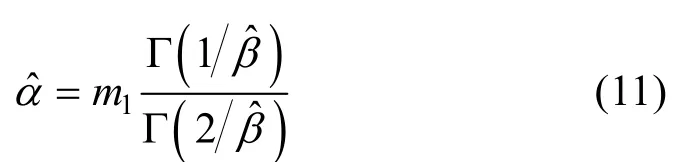
3.2 Cauchy分布及其参数估计

大量研究表明，α-稳定分布非常适合用来建模具有高尖峰、长拖尾分布特征的随机变量。一个随机变量X服从α-稳定分布，X ～Sα（γ, β,δ），特征函数具备如下形式[18]：

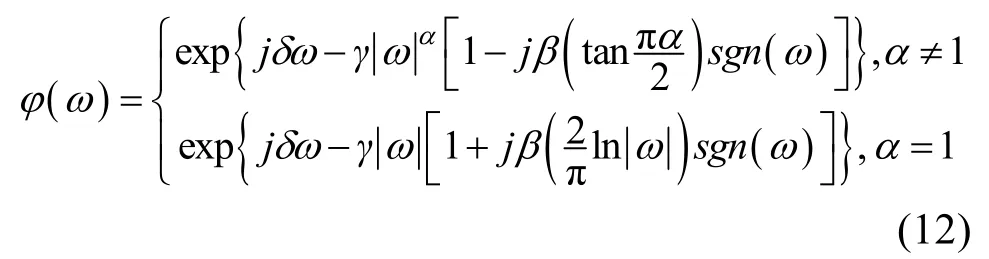
其中符号函数：

当β=0时，Sα（γ, β,δ） 称为对称α-稳定分布(symmetric α-stable distribution，SαS)。δ=0时SαS的概率密度函数当α=1(Cauchy分布)，α=2(高斯分布)时才存在封闭的显式形式，其他情况下的概率密度函数可以通过幂级数展开实现[18]。

SαS已经被用来建模 DCT的交流系数[19]、Curvelet变换系数[20]以及 CT系数[10,18]的统计特性。由于SαS的概率密度函数当0＜α＜1以及1＜α＜2时不存在封闭的显式形式，为降低计算复杂度，同时简化水印检测器的设计，文献[10] 和[19-20]均采用了SαS当α=1时的特例 Cauchy分布描述系数的统计特性。

参数γ可用极大似然估计法[21]求得，其中同样需要用到New ton-Raphson迭代的数值方式，初值选取及迭代过程参见文献[21]。

本文采用一种快速方法[21-22]来估计参数γ。由于服从Cauchy分布的随机变量不存在有限的总体矩，参数γ的矩估计值不存在。作为SαS的一个特例，参数γ的一种快速估计法为：

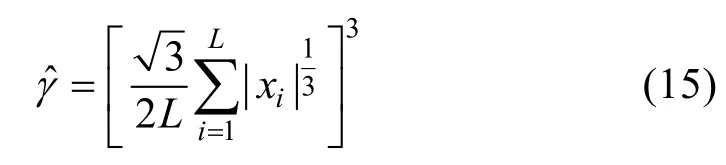
本文在参数估计时用式(9)、(11)和(15)给出的快速参数估计法。

4 NSCT系数的统计特性

本文的统计特性是指系数的边缘统计模型，即将子带系数视为从总体中抽样的结果，这些系数是服从独立同分布(independent identically distributed，IID)的随机变量。边缘统计建模的任务是为总体寻找一个合适的概率分布模型，通过子带系数做参数估计，进而获得总体的概率分布模型，为水印检测器的设计提供依据。

为直观分析 NSCT系数的边缘统计特性，给出测试图像“Lena”在l=0尺度上 8个方向子带系数的直方图，如图1所示。

图 1表明，变换系数在零点附近呈现近似对称分布，且近似在零点处形成一个高尖峰，即变换系数具有明显的非高斯性。同时，分布的两边有长拖尾。为定量衡量一个随机变量的非高斯性，这里采用峰度(Kurtosis)指标。一个随机变量 x的峰度定义为：

高斯分布的峰度为3。若随机变量x服从超高斯分布，其峰度大于3，峰度越大，分布越陡峭，形成高尖峰。若随机变量x服从亚高斯分布，其峰度小于3，峰度越小，分布越平坦。表2给出了测试图像“Lena”在4个尺度上的所有方向子带系数的峰度。

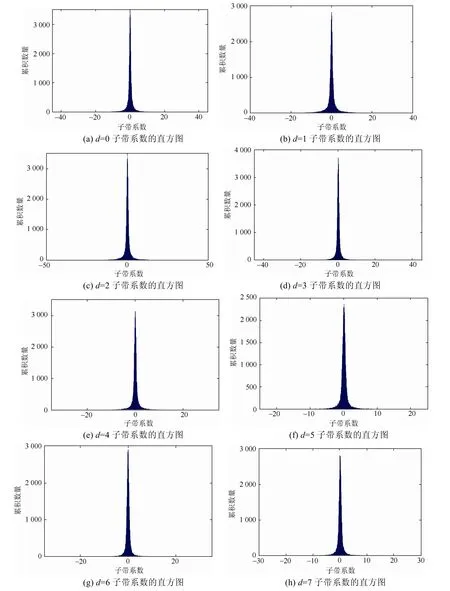
图1 “Lena”在l=0尺度上8个方向子带系数的直方图

表2 “Lena”在4个尺度上的所有方向子带系数的峰度值

由图1及表2可见，测试图像“Lena”的NSCT高频方向子带系数服从超高斯分布，且具有明显的长拖尾特性。本文分别用零均值GGD和δ=0的Cauchy分布作为NSCT高频方向子带系数的统计模型，以此分别设计相应的水印检测器。图 2给出了l=0，d=2子带系数的拟合结果，由图2可见Cauchy分布的拟合效果较好。

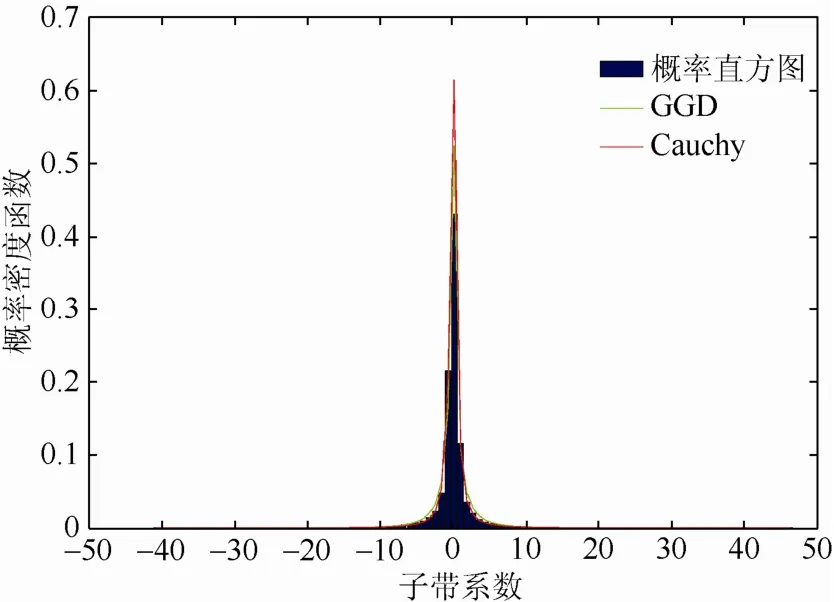
图2 子带系数两种统计分布模型的拟合结果

5 水印的嵌入算法

水印的嵌入算法如下：

(1) 将原始图像分解为4个尺度(l=0，1，2，3)，每个尺度上的方向子带数目都分解为8，用密钥生成[–1,1]区间上均匀分布的伪随机序列作为水印信息。

(2) 水印信息选择嵌入在l=0尺度上能量最大的方向子带中，方向子带的能量计算公式为：

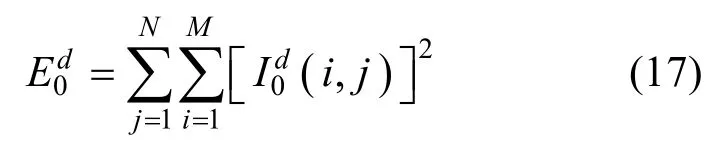
(3) 按乘性规则嵌入水印：

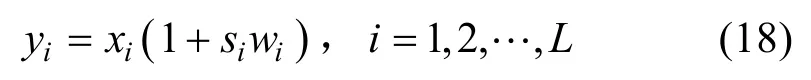
(4) 逆变换得到含水印图像。

图3给出了水印嵌入算法的流程图。

图3 水印嵌入算法的流程图

6 水印的检测算法

水印的统计检测需要作一些基本假设，这被目前较多的研究所忽视，完整的基本假设参见文献[23]。

6.1 自适应乘性水印的检测统计量

设 NSCT方向子带系数总体的概率密度函数为p（x） ，考虑自适应乘性水印的统计检测问题，在s未知的盲检测要求下，水印的检测问题可表述为一个复合假设检验[8]：

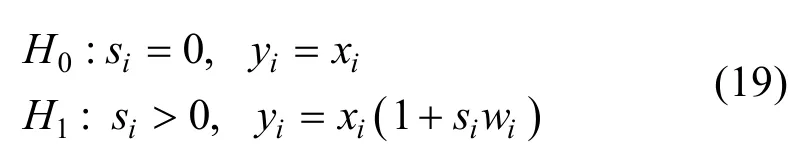
局部最大势(locally most powerful，LMP)检测器(也称局部最优检测器，locally optimal detector，LOD)有两种实现方式[23]：①由其定义实现，LMP检测器的势函数(检测概率)在 s=0处的斜率的绝对值达到最大[8]；②将对数似然比在s =0处进行泰勒级数展开，忽略平方项及更高次幂项[20]。本文与文献[8]一样，采用第①种方式。在2种假设下，检测器接收到向量y的条件概率密度分别为：

则LMP检测统计量为[23]：

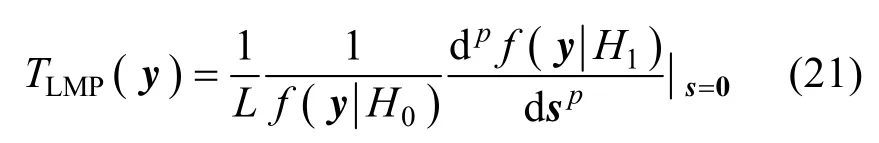
其中，p是使得势函数导数非零的最小值，取p=1，LMP检测统计量简化为：

6.2 两种分布模型下的LMP检测统计量

在GGD模型下，式(20)可写为：

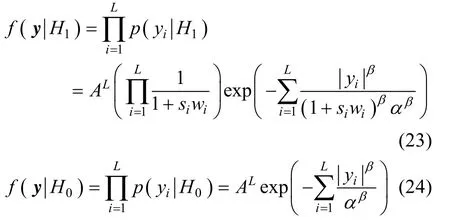
为推导方便，记：

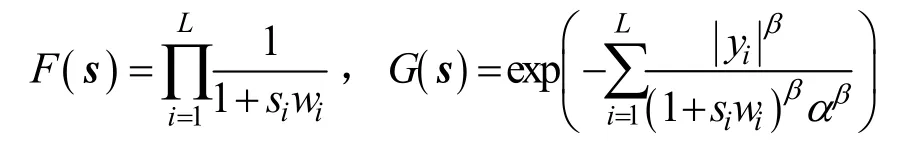
则：

利用式(25)和(26)可得：

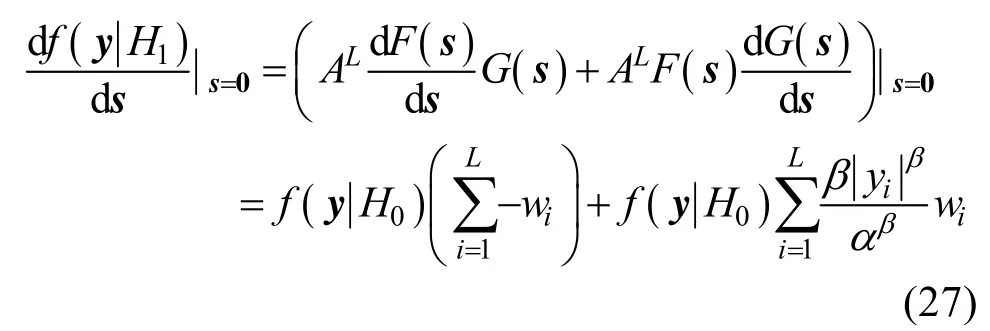
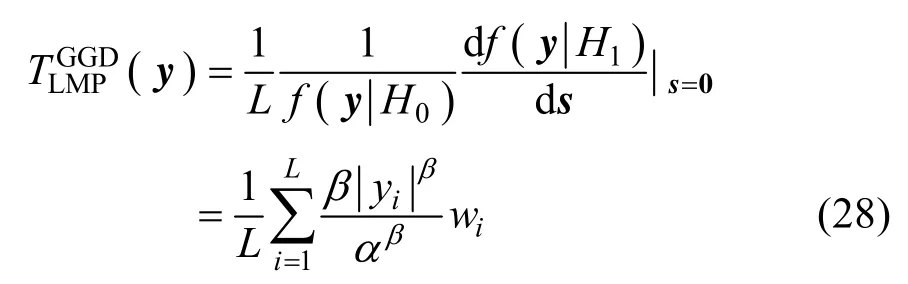
在Cauchy分布模型下，式(20)可写为：

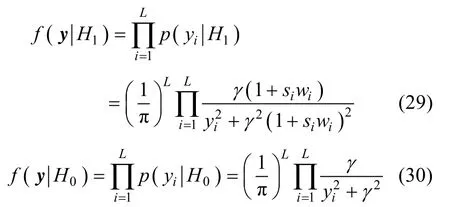
经导数计算及一系列整理，得：

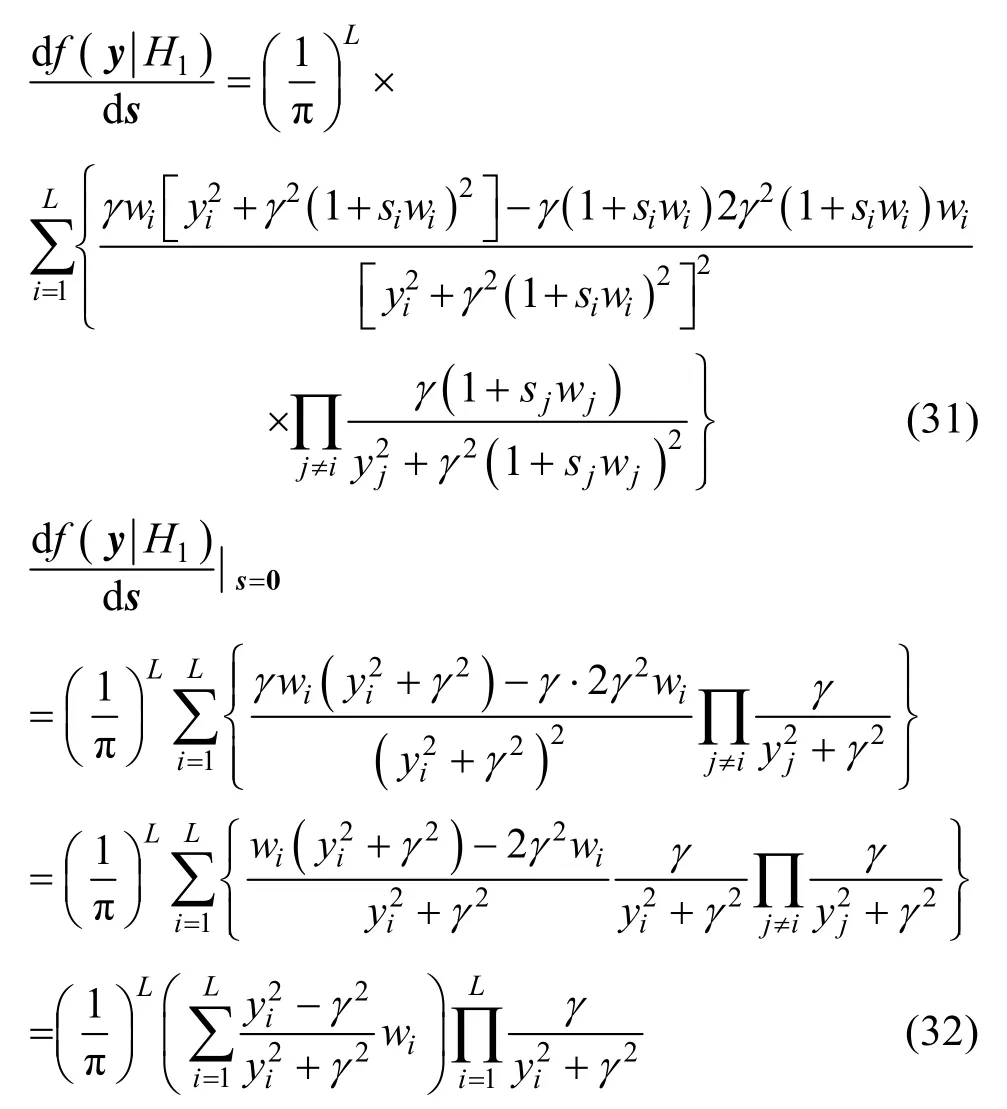
此时LMP检测统计量(Cauchy检测器)为：

6.3 LMP检测门限的确定

水印检测通常使用纽曼-皮尔逊(Newman-Pearson，NP)准则。该准则在保证虚警概率不超过给定值的约束条件下，使得检测概率最大。检测器门限由指定的虚警概率确定。

设在H0之下，LMP检测统计量的均值和方差分别为：

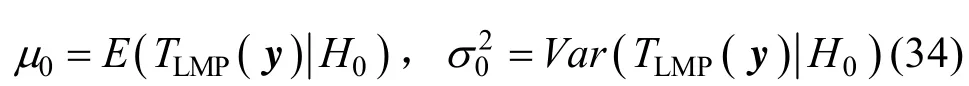
在H1之下，LMP检测统计量的均值和方差分别为：

由中心极限定理可知，TLMP（y）在H0和H1之下均渐进服从高斯分布，将其归一化，指定虚警概率Pfa，则Pfa与门限λ的关系为：

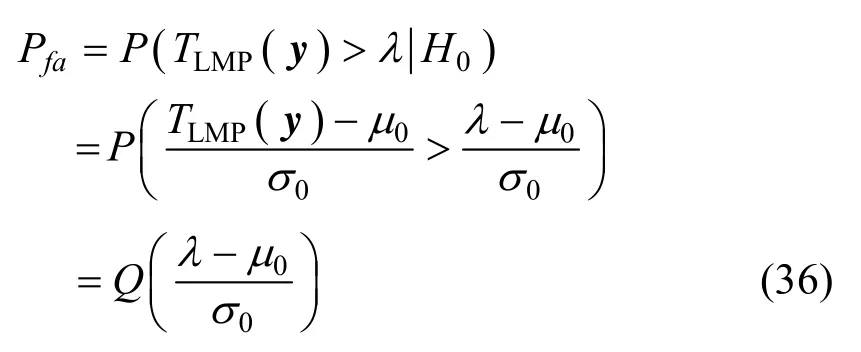
其中， Q-1为Q的反函数。

6.4 两种分布模型下0μ和的确定

在GGD模型下，当H0为真时， yi=xi，此时，

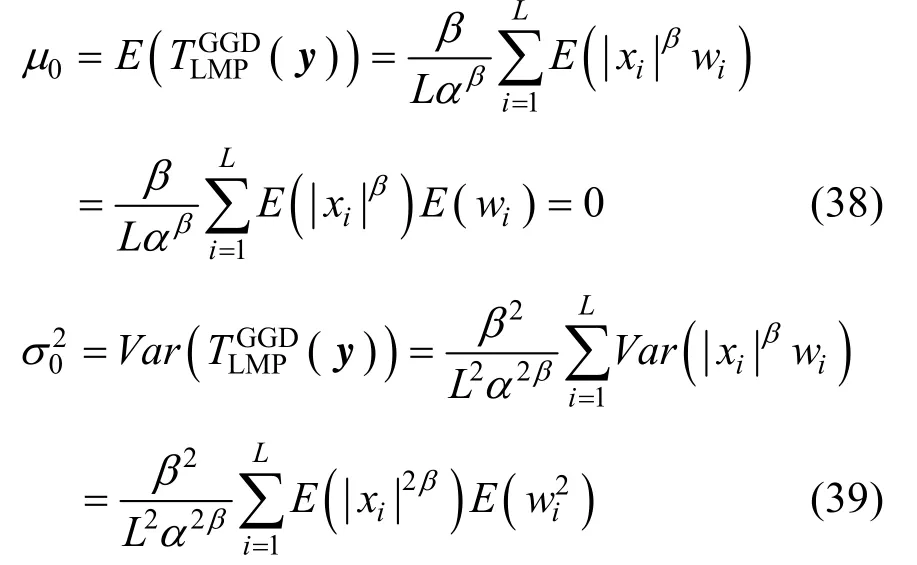
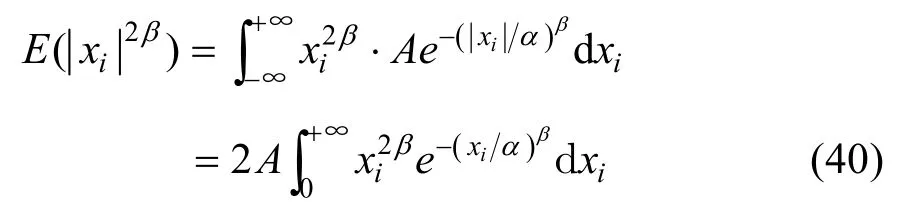
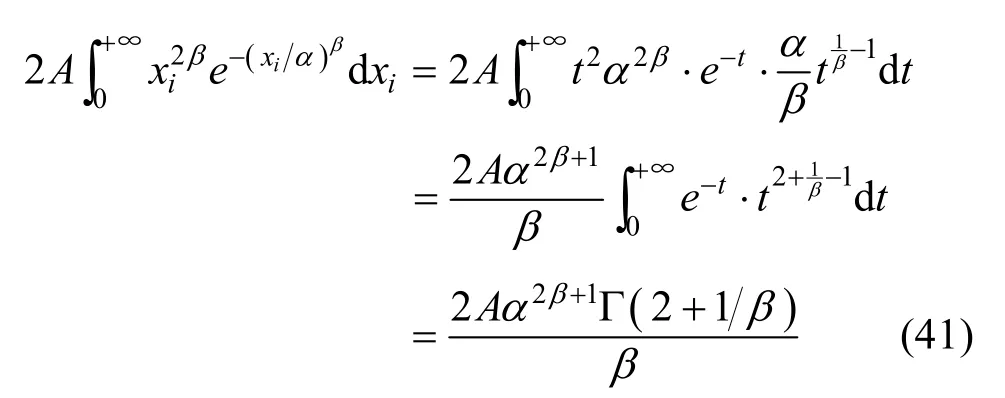
将式(41)代入式(39)，得：

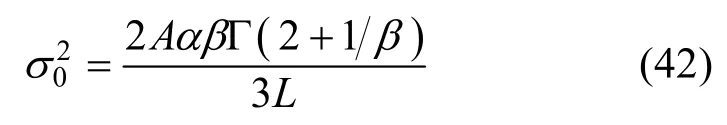
在Cauchy分布模型下，当H0为真时，yi=xi，此时，

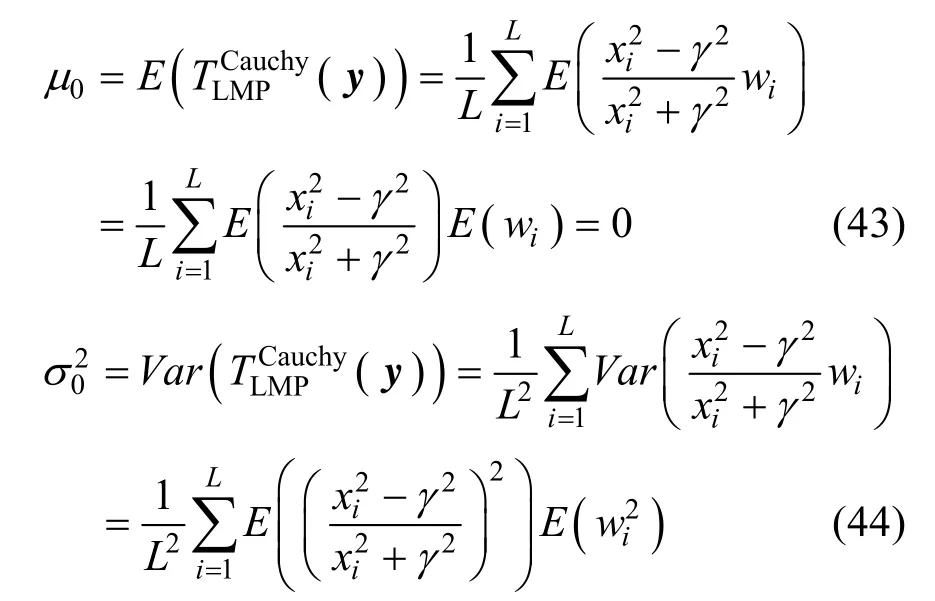
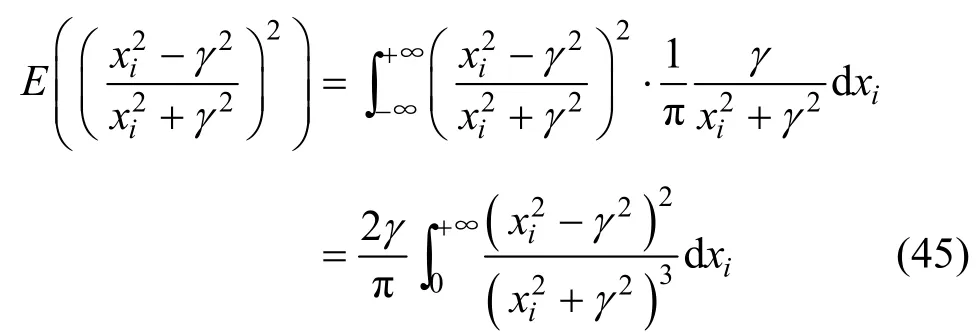
式(45)中令 xi=γt anθ ，经过一系列计算可得：

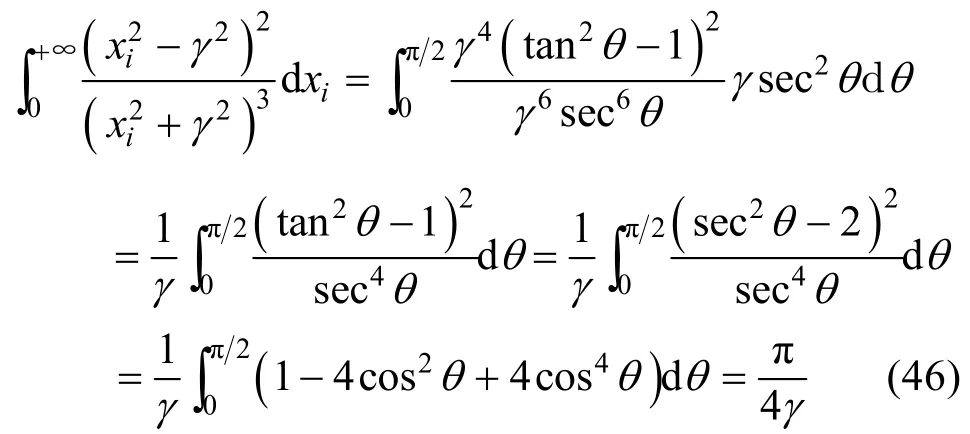
此时，

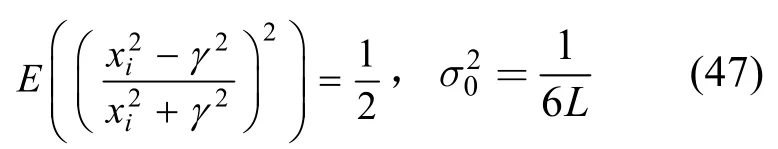
6.5 水印的检测算法

(1) 用NSCT将待检测图像作与嵌入算法步骤中相同的分解，获得待检测子带。

(2) 在盲检测要求下，原始图像无法获得，可用快速估计法估计待检测子带的统计模型参数，以此替代原始图像的统计模型参数[8]。

(3) 指定虚警概率，获得相应的检测门限。

(4) 检测器已知水印信息，由此计算LMP检测统计量并与检测门限比较，判决水印是否存在。

表 3列出了本文推导出的检测器结构及检测门限中的参数值。图 4给出了水印检测算法的流程图。

表3 检测器结构及检测门限中的参数值

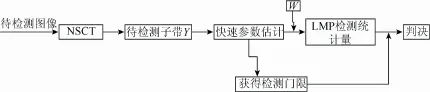
图4 水印检测算法的流程图

7 实验与分析

本文实验平台为MATLAB R2012b，实验图像为256×256的“Lena”和“Barbara”灰度图像，NSCT工具包采用“dmaxflat7”和“maxflat”滤波器，该工具包可从作者主页获得。计算机处理器为Intel Core i3-4150，3.50 GHz，内存为4 GB。

7.1 掩盖效应和不可见性

图 5(b)、(d)是按式(1)～(4)计算得到的“Lena”和“Barbara”图像NSCT系数的掩盖效应图(为视觉效果，图像经过了放大)。亮度较大的位置上允许较大的嵌入失真。

图5 测试图像的掩盖效应图

对图6(a)、(c)的含水印图像，用SSIM[24]作为客观指标衡量图像的质量，其值分别为 0.9932、0.9836(由作者提供的 ssim.m代码中 Basic Usage计算得到)，表明本文提出的NSCT域掩盖效应计算模型较好地满足了水印嵌入的视觉不可见性要求。

图 6(b)、(d)为含水印图像与原始图像的差值图像(为视觉效果，图像经过了放大)，可以看出差值基本都集中在边缘部分，这和掩盖效应图的结果是一致的。

7.2 两种检测器的检测结果及比较

用密钥控制生成1 000个伪随机水印序列，其中第500个为嵌入的水印序列，图7分别给出了“Lena” 和“Barbara”图像的GGD检测器和Cauchy检测器的检测结果(虚警概率设置为 10–8，图中的水平虚线表示当前的检测门限)。

图6 含水印图像及其与原始图像的差值图像

文献[2-5]虽然考虑了变换系数的视觉掩盖，但是没有考虑系数的统计特性，且水印嵌入使用了简单的加性方式，因此检测算法相对容易实现。本文提出用GGD及Cauchy分布描述NSCT系数的统计特性，使用统计判决理论，实现了相对较复杂的乘性水印的统计检测。

注意到文献[7]和[10]均使用固定嵌入强度，且检测器需要固定嵌入强度的数值，其实质是UMP检测器。本文算法考虑了NSCT系数的视觉掩盖，每个系数的嵌入强度均不相同，这使得盲检测实现比较困难。即便如此，图 7表明本文提出的两种局部最优非线性盲检测器在无原始图像和自适应嵌入强度系数参与检测的情况下均准确地检测到水印信息的存在。

观察图7可以发现，GGD检测器在第500个水印序列处的响应值虽然高于检测门限，但是高出的幅度不大，同时其他个别水印序列的响应值比较大，接近检测门限，可能会出现虚警错误；Cauchy检测器在第500个水印序列处的响应值明显高于检测门限，其他水印序列的响应值均比较小，远低于检测门限。这表明Cauchy检测器的性能优于GGD检测器。

图7 两种检测器的检测结果比较

表4给出了GGD检测器和Cauchy检测器的检测耗时对比(这里的检测耗时是指从待检测子带的统计模型参数估计到检测器计算出检测门限和1 000个水印序列的检测响应值所消耗的时间)。可以看出，Cauchy检测器的耗时远小于 GGD检测器，这主要得益于Cauchy检测器只需要估计一个参数，检测器的结构也比较简单，检测门限中的参数为常数。

表4 两种检测器的检测耗时比较(s)

8 结 束 语

本文提出了一种基于 NSCT的自适应乘性水印算法，该算法结合了当前两类图像水印算法的特点，同时考虑了 NSCT域掩盖效应计算模型和NSCT方向子带系数的统计特性。算法的主要特点包括：

(1) 借鉴 Barni的“pixel-w ise masking”模型和冗余小波域掩盖效应建模的做法，建立了 NSCT域掩盖效应计算模型。该模型使得算法具有良好的视觉不可见性。

(2) 对于具有高尖峰、长拖尾分布的NSCT变换系数，提出用GGD及对称α-稳定分布(SαS)的特例Cauchy分布描述其统计特性，讨论了两种统计模型的参数估计问题。

(3) 本文算法考虑了系数的掩盖效应，因此各系数的嵌入强度均不相同，但是得益于将水印检测表述为一个复合假设检验，理论计算推导出的NSCT域乘性水印局部最优非线性GGD盲检测器和Cauchy盲检测器均不需要原始图像和自适应嵌入强度系数参与检测。通过理论计算，本文还进一步给出了上述检测器检测门限的自适应确定方法。

实验证实本文算法具有良好的视觉不可见性，且两种检测器在无原始图像和自适应嵌入强度系数参与检测的情况下均能准确地检测到水印信息的存在。同时，实验也表明Cauchy盲检测器的性能优于GGD盲检测器。

[1] Barni M, Bartolini F, Piva A. Improved wavelet-based watermarking through pixel-w ise masking [J]. IEEE Transactions on Image Processing, 2001, 10(5): 783-791.

[2] Baaziz N. Adaptive watermarking schemes based on a redundant contourlet transform [C]//IEEE International Conference on Image Processing. New York: IEEE Press, 2005, 1: 221-224.

[3] 陈开亮, 王建军. 一种HVS和Contourlet结合的图像水印算法[J]. 计算机辅助设计与图形学学报, 2007, 19(6): 811-816.

[4] Song H H, Yu S Y, Yang X K, et al. Contourlet-based image adaptive watermarking [J]. Signal Processing: Image Communication, 2008, 23(3): 162-178.

[5] 丁兴号, 章登峰, 钱 坤, 等. 基于无下采样Contourlet变换和人眼视觉系统的稳健盲水印算法[J].光学学报, 2009, 29(12): 3344-3350.

[6] 梁 婷, 李 敏, 何玉杰, 等. 基于人类视觉系统的非抽样 Contourlet变换域图像隐写算法[J]. 计算机应用, 2013, 33(1): 153-155.

[7] 李海峰, 宋巍巍, 王树勋. 基于Contourlet变换的稳健性图像水印算法[J]. 通信学报, 2006, 27(4): 87-94.

[8] Cheng Q, Huang T S. Robust optimum detection of transform domain multiplicative watermarks [J]. IEEE Transactions on Signal Processing, 2003, 51(4): 906-924.

[9] Akhaee M A, Sahraeian S, Marvasti F. Contourlet-based image watermarking using optimum detector in a noisy environment [J]. IEEE Transactions on Image Processing, 2010, 19(4): 967-980.

[10] Sadreazam i H, Omair Ahmad M, Swamy M N S. A study of multiplicative watermark detection in the contourlet domain using alpha-stable distributions [J]. IEEE Transactions on Image Processing, 2014, 23(10): 4348-4360.

[11] Do M N, Vetterli M. The contourlet transform: an efficient directional multiresolution image representation [J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106.

[12] Candes E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms [J]. Multiscale Modeling & Simulation, 2006, 5(3): 861-899.

[13] 冯 鹏. 高分辨图像处理用抗混叠 Contourlet变换的若干关键问题研究[D]. 重庆: 重庆大学, 2007.

[14] da Cunha A L, Zhou J P, Do M N. The nonsubsampled contourlet transform: theory, design, and applications [J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101.

[15] Parker K M, Fow ler J E. Redundant-wavelet watermarking with pixel-w ise masking [C]//IEEE International Conference on Image Processing. New York: IEEE Press, 2005, 1: 685-688.

[16] Do M N, Vetterli M. Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance [J]. IEEE Transactions on Image Processing, 2002, 11(2): 146-158.

[17] 汪太月, 李志明. 一种广义高斯分布的参数快速估计法[J]. 工程地球物理学报, 2006, 3(3): 172-176.

[18] Sadreazam i H, Omair Ahmad M, Swamy M N S. Contourlet domain image modeling by using the alpha-stable family of distributions [C]//IEEE International Symposium on Circuits and Systems. New York: IEEE Press, 2014: 1288-1291.

[19] Briassouli A, Tsakalides P, Stouraitis A. Hidden messages in heavy-tails: DCT-domain watermark detection using alpha-stable models [J]. IEEE Transactions on Multimedia, 2005, 7(4): 700-715.

[20] Deng C Z, Zhu H S, Wang S Q. Curvelet domain watermark detection using alpha-stable models [C]// Fifth International Conference on Information Assurance and Security. Washington DC: IEEE Computer Society, 2009, 1: 313-316.

[21] Kw itt R, Meerwald P, Uhl A. Lightweight detection of additive watermarking in the DWT-domain [J]. IEEE Transactions on Image Processing, 2011, 20(2): 474-484.

[22] Tsihrintzis G A, Nikias C L. Fast estimation of the parameters of alpha-stable impulsive interference [J]. IEEE Transactions on Signal Processing, 1996, 44(6): 1492-1503.

[23] Bian Y, Liang S. Locally optimal detection of image watermarks in the wavelet domain using Bessel K form distribution [J]. IEEE Transactions on Image Processing, 2013, 22(6): 2372-2384.

[24] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity [J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612.

Locally Optimal Nonlinear Blind Detection A lgorithm for Adaptive Multip licative Watermarks in NSCT Domain

Ye Jianbing, Zhang Wenbin

(Taizhou Institute of Science & Technology, Nanjing University of Science & Technology, Taizhou Jiangsu 225300, China)

Research of image watermarking algorithms is an important issue in the field of multimedia technology. By comparing and combing the current two leading watermarking algorithms, an adaptive multiplicative watermarking algorithm is proposed. Motivated by Barni’s “pixel-w ise masking” model and redundant wavelet domain masking effect modeling approach, the nonsubsampled Contourlet transform domain masking effect model is established. With generalized Gaussian distribution model and Cauchy distribution model to describe the statistical properties of the nonsubsampled Contourlet transform coefficients, the watermark detection problem is then addressed as a composite hypothesis testing. Theoretical analysis leads to two locally optimal nonlinear blind detectors for adaptive multiplicative watermarks as well as adaptive methods for determ ining detection thresholds. The experiment results show that the nonsubsampled Contourlet transform domain masking model achieves good visual invisibility, and watermarks can be accurately detectedwithout using the original images and the adaptive embedding strength factors. In addition, Cauchy distribution based blind detector is found superior to the blind detector based on the generalized Gaussian distribution both in terms of detection performance and detection efficiency.

nonsubsampled Contourlet transform; generalized Gaussian distribution; symmetric α-stable distribution; Cauchy distribution; adaptive multiplicative watermarks; locally optimal nonlinear detector; blind detector

TP 37

10.11996/JG.j.2095-302X.2016030417

A

2095-302X(2016)03-0417-11

2015-08-03；定稿日期：2015-11-13

江苏省高校自然科学研究面上项目(14KJD110004)

叶建兵(1981–)，男，江苏泰兴人，讲师，硕士。主要研究方向为多尺度几何分析与数字图像处理。E-mail：jbyetz@163.com