基于频谱边缘检测和Radon变换估计运动模糊图像的方向

加春燕， 崔 丽

(1. 北京工业职业技术学院基础教育学院，北京 100042；2. 北京师范大学数学科学学院，北京 100875)

基于频谱边缘检测和Radon变换估计运动模糊图像的方向

加春燕1， 崔 丽2

(1. 北京工业职业技术学院基础教育学院，北京 100042；2. 北京师范大学数学科学学院，北京 100875)

为了准确估计运动模糊图像的方向，在理论推导部分，以定积分、Fourier变换和Sinc函数的性质为依据，得出了运动模糊方向、图像尺寸和频谱图像平行条纹方向三者的关系。在算法优化部分，系统分析了Radon变换法、Gabor变换法和频谱分块法的原理和不足，并提出了基于频谱边缘检测和Radon变换的改进算法。在数值实验部分，编写Matlab程序对几种方法进行了测试和比较，结果表明，该方法的估计精度最高，更适用于估计运动模糊图像的方向。

运动模糊图像的方向估计；频谱边缘检测；Radon变换；Gabor变换；频谱分块法

实际成像过程中，因相机与被摄物体之间的相对运动而造成的模糊通常被称为运动模糊，运动模糊图像的恢复在天文、军事、道路交通及医学图像等各个领域中都有广泛的应用。由于运动模糊效应取决于运动方向和运动长度，且运动长度的估计又依赖于运动方向的估计[1]，故本文研究了运动方向的估计方法。目前估计运动方向最常用的是Radon变换法[2]，根据频谱图像中的平行条纹特征来估计运动方向，容易操作且准确度较高，但当运动长度较小或图像受到噪声干扰时，由于频谱图像中的条纹特征不显著且受到频谱中心亮十字的干扰，导致估计误差较大，对其改进较好的方法包括 Gabor变换法[3]和乐翔等[4]提出的频谱分块法，但这两种算法的运算量较大不易操作，且未考虑图像尺寸问题。为此，本文先进行理论分析，推导图像尺寸、运动模糊方向角和频谱图像中的平行条纹方向角三者的关系，再寻找一种改进算法，既能突出频谱图像的条纹特征，又能保证运算量较小容易操作，且估计精度要高于现有的方法。此外，对于实拍的运动模糊图像，利用本文算法估计方向角后再进行图像恢复，要保证恢复效果较好，才能体现本文算法的应用价值。

1 理论推导

将图像视为点集，每点对应一个像素值，可记为 f( x,y)，其中x和y代表该点的行、列位置。运动模糊过程可以理解为：一幅本来清晰的图像f，受到运动模糊(其核函数记为kL,α)及其他细微噪声r(如光照等，理想状态下可视为0)的“污染”，退化为实际观测到的图像g，这一现象可用如下卷积方程来刻画：

其中，kL,α通常被称为运动模糊核函数，L代表运动模糊长度，α代表运动模糊方向角。由于变速非直线的运动可分解为分段匀速直线运动，因此本文提到的运动模糊均指匀速直线运动模糊，即L 和α均为常数。图像恢复的目的就是从 g入手，结合kL,α和r的相关信息来重构图像，重构结果越清晰越好。显然，准确估计运动模糊参数L和α是前提，事实上，一旦估计出α，便可将二维图像在该方向上降解为一维数据，从中容易算出L[1]，估计运动模糊方向角α的推导过程如下：

(1) 为方便推导，暂不考虑其他噪声(r=0)，设x0(t)和y0(t)分别为t时间内像素点在x和y方向上的变化分量，T为相机曝光时间，于是有：

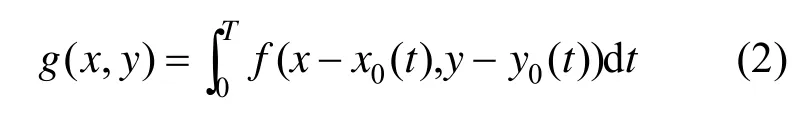
(2) 对式(2)进行Fourier变换，记G、F和K分别为g、f和kL,α的Fourier 变换函数，则：

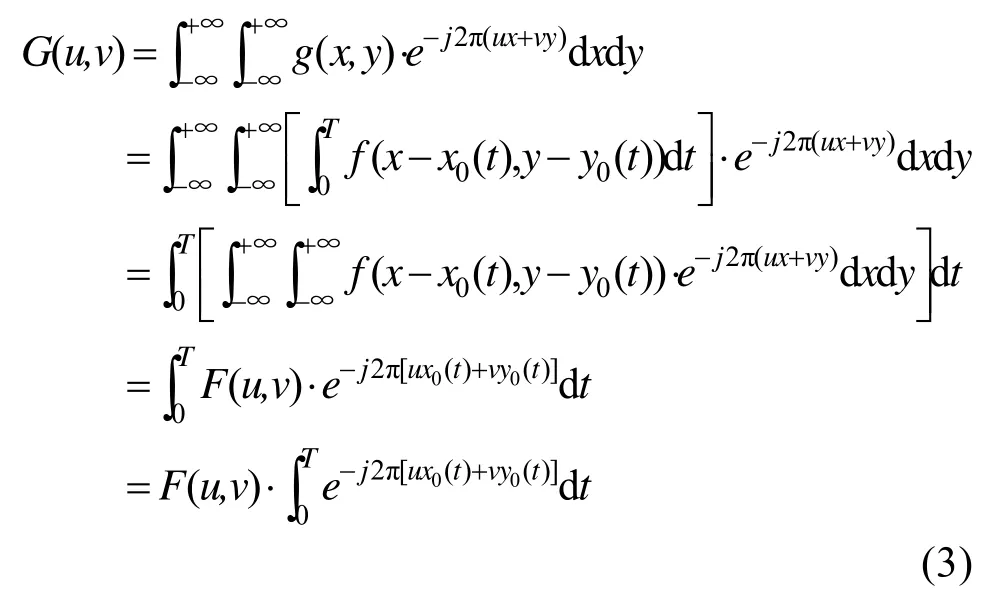
因此 kL,α(x,y)的Fourier变换函数 K( u, v)为：

(3) 设a、b是在曝光时间T内像素点在x、y方向上移动的距离，则：

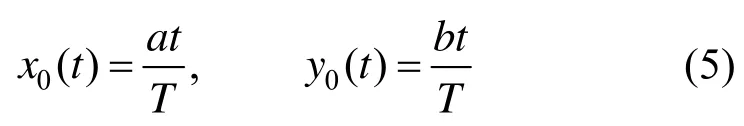
代入式(4)，计算定积分可得：

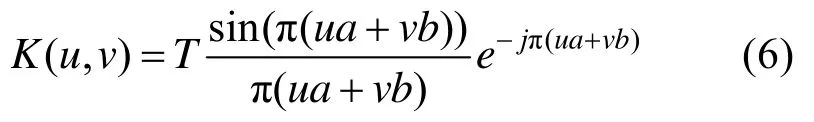
(4) 设图像尺寸为M×N，对式(6)进行离散化得：

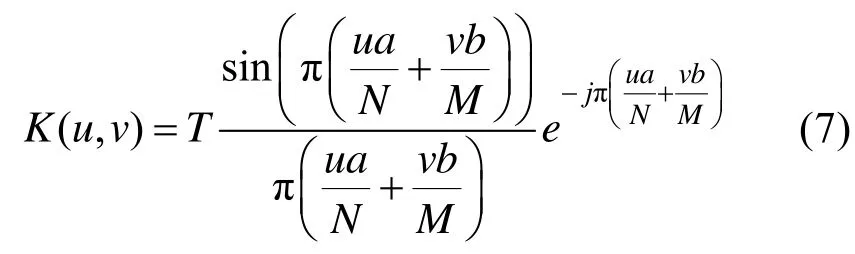
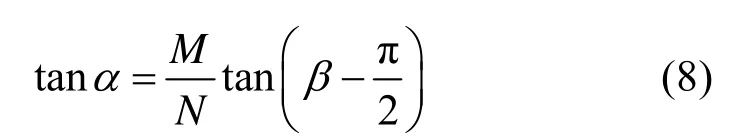
显然，当图像为方图即M=N时，模糊方向与暗条纹方向垂直，这也是大多数文献所使用的结论[1-4]，但当M和N不等时二者并不垂直。图1通过两个测试图像展示了式(8)中的角度关系，其中图 1(a)和(c)中的运动模糊方向角α的真实值均为45°，用本文 2.3节的方法检测出图 1(b)中平行条纹方向角β为135°，代入式(8)得α估计值为45°，同理图1(d)中β为153°，代入式(8)得α约为44.8°，与45°十分接近。

图1 运动模糊图像及其频谱图像

2 运动模糊图像方向的估计方法

2.1 Radon变换方法及其不足

为估计运动模糊方向角α，由式(8)需要先检测频谱图像中的平行暗条纹方向角β，目前应用较多的是Radon变换方法，对于频谱图像G，其Radon变换为[2]：

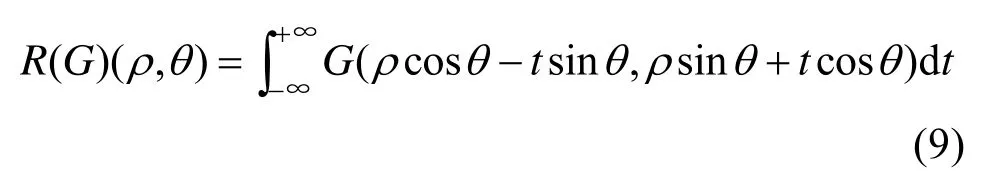
可见，G的Radon变换是沿着距原点(图像中心)ρ且与Y轴方向夹角为θ的线积分，由于运动模糊频谱图中有一组平行条纹(图1(b)和(d))，则沿该方向的积分值必然最大，故而通过 Radon变换求最大值便可确定平行条纹的方向。但 Radon变换存在不足：①当模糊长度 L较小时频谱图中的平行条纹较少，此时用 Radon变换检测不准；②频谱图像中心处的亮十字(图 1(b)和(d))对 Radon变换的干扰较大，会误检为0°或90°。例如，对图1(b)和(d)做Radon变换(图2)，结果为90°和63°，真实值应是45°和63°(倾斜角β为153°，与Y轴夹角θ为63°)，在此，对图1(b)误检为90°了。亮十字出现的原因，是因为当kL,α与f做完全卷积时，所得图像 g的宽和高应比 f分别增加L cosα和L sinα ，然而，实际中相机成像空间固定，所得图像在四周边缘处会被截断，陡峭的边缘截断导致中心化后的频谱图像中心出现了亮十字。大多数文献未考虑此问题，因为测试图像可以先进行边界处理，但实拍图像必然会有边缘截断，因此如何有效地消除亮十字是值得处理的问题。

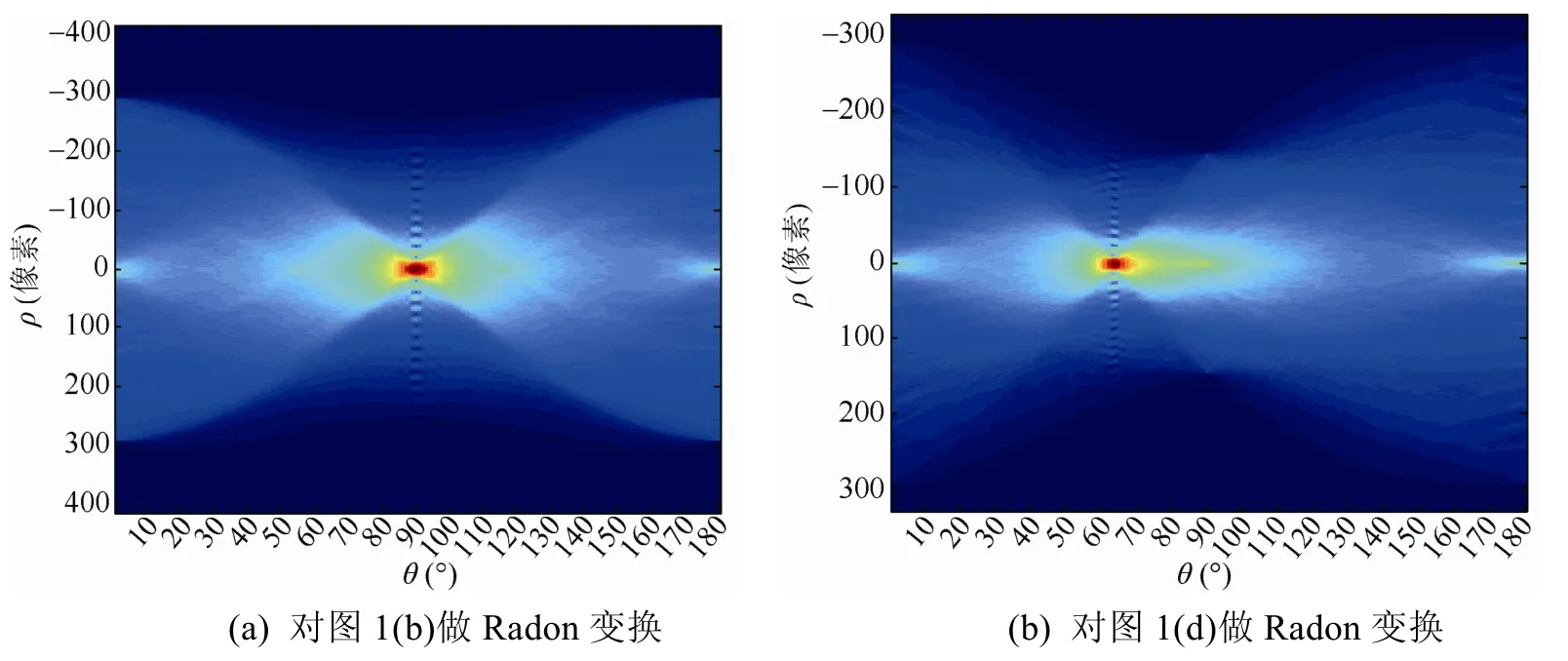
图2 图1(b)和(d)分别做Randon变换检测条纹方向

2.2 两种改进方法及其不足

基于上述分析，改进 Radon变换应致力于两个目标：①设法突出频谱图像中的平行条纹特征；②设法消除频谱图像中的亮十字。Gabor变换方法[3]是用Gabor变换将“窗口”聚焦图像中心，从而减少了亮十字的干扰，但窗口函数(Gassian函数)中的参数需人为设定，实用性不强。乐翔等[4]提出了频谱分块的方法，具体作法是先检测出亮十字位置，然后截取去除十字后的 1/4块来做 Radon变换，对图1(b)和(d)，可取十字的左上或右下块，缺点是检测亮十字位置的运算量较大容易出错，且对于小尺度运动模糊情形误差较大。此外，这两种改进算法处理的均为方图，默认了模糊方向与频谱平行暗条纹方向垂直，未考虑图像长宽不等的情形。

2.3 基于频谱边缘检测和Radon变换的改进方法

边缘检测旨在提取目标与背景之间在灰度或者纹理特征上的突变边界线，频谱图像中有明显的亮暗相间的条纹，对其做边缘检测所得边界线应与条纹方向平行，且能够弱化亮十字的高灰度值，从而降低亮十字干扰。常用的边缘检测算子有Sobel算子、Laplacian of Gaussian(LoG)算子和Canny算子等，本文选用检测性能较好的 Canny算子，采用先平滑后求导数的方法，边缘点位于图像被高斯平滑后的梯度值的极大值点[5]。对图 1(b) 和(d)做Canny边缘检测(图3(a)和(b))，突出了平行暗条纹的轮廓，虽然亮十字仍隐约可见，但相比强化后的平行边界线，其干扰已经变得很微弱。

图3 对图1(b)和(d)先做Canny边缘检测再做Radon变换

根据前面的理论分析，改进的运动模糊方向角的估计算法如下：

(1) 通过二维 Fourier变换，求运动模糊图像的频谱G，且通常利用取对数来压缩频谱的灰度值范围，增强暗条纹特征，一般取ln (1+|G|)；

(2) 使用 Canny算子对(1)中的结果进行边缘检测；

(3) 对(2)得到的二值化频谱做 0°～180°的Radon变换，找出变换最大值对应的角度θ，该角度为频谱暗条纹方向与 Y轴的夹角，因此暗条纹的倾斜角为；

(4) 结合图像尺寸M和N代入式(8)，算出运动模糊方向角α。

借助Matlab软件编写程序，对图3(a)和(b)做Radon变换，结果见图3(c)和(d)，θ分别为45°和63°，于是β为135°和153°，代入式(8)计算，得到α分别为45°和44.8°，两者的真实值均为45°，可见估计结果较为准确。

3 数值实验及结果分析

为进一步验证算法的准确性，选择图 1中的512×512大小的轿车图和截取的 256×512车牌图进行实验，实验中先用 Matlab工具箱中的“fspecial”命令人为设置运动模糊，模糊角度α取5°、45°、80°和150°，模糊长度L取8、20和40，分别按照Gabor变换方法[3]、频谱分块方法[4]和本文算法对α进行估计，实验结果给出了估计值及相应的误差绝对值(表1～2)，其中角度的小数位按四舍五入取整。

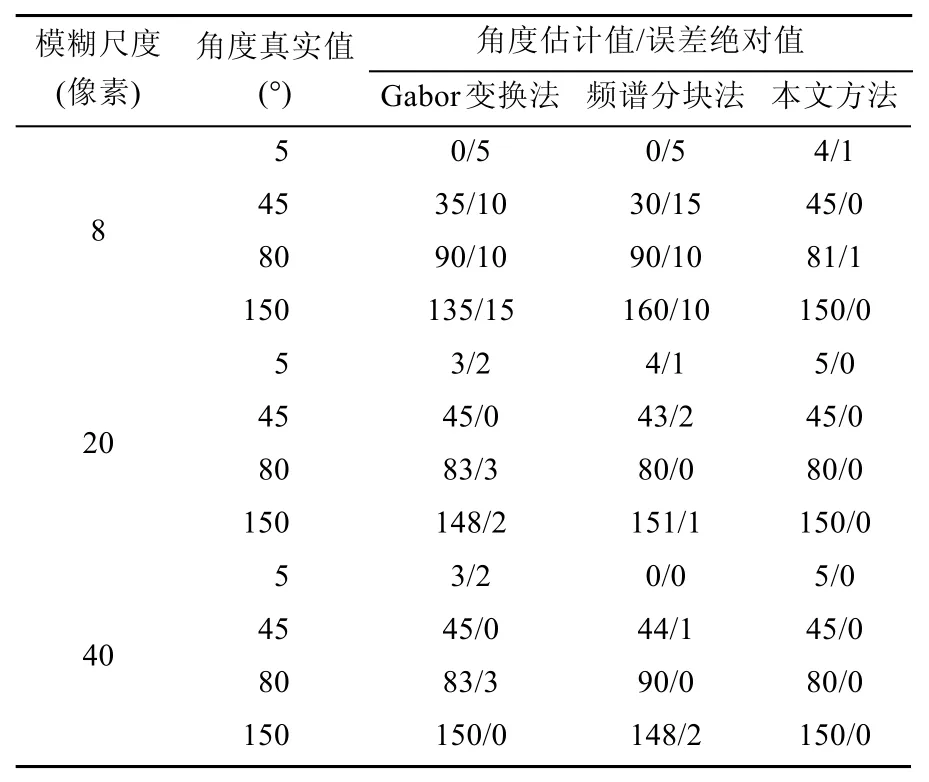
表1 512×512轿车图像实验结果

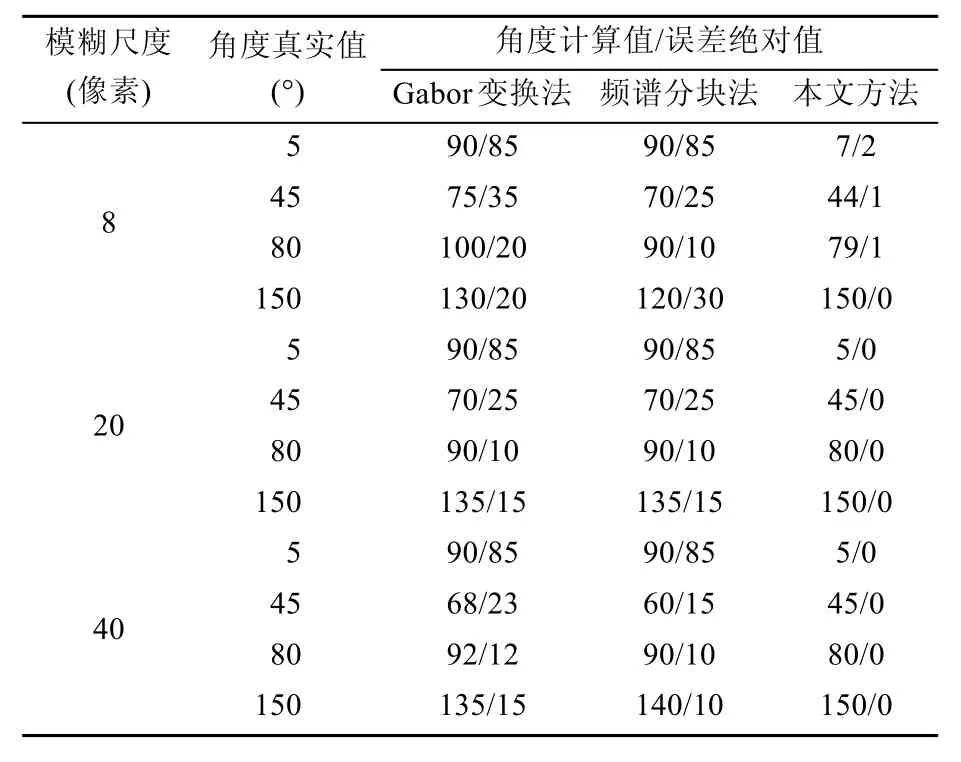
表2 256×512车牌图像实验结果

表2数据显示，当图像长宽不相等时，由于文献[3]和[4]错误地默认了频谱暗条纹方向与模糊方向垂直，因此估算结果出错，而本文算法考虑到图像尺寸、频谱暗条纹方向和模糊方向三者之间的关系，按照式(8)进行计算，最终估计结果比较准确，仅在小尺度模糊时出现了1或2像素的误差。

图 4展示了实拍的运动模糊车牌图像及其恢复结果，对于第一行的车牌图像，α角的估计结果：本文算法为150°，Gabor变换法为145°，频谱分块法为143°，长度L用文献[6]的方法计算分别为13像素、10像素和8像素，按文献[7]的方法对图像进行恢复，从图 4可以看出，本文算法恢复效果最好。第二行是车辆过收费站时的模糊图像，从中截取了车牌部分进行参数估计，本文算法估计出α为0°，L为6像素，Gabor变换法的结果为5°和10像素，频谱分块法的结果为12°和20像素，对应的恢复效果见图4，仍然是本文算法恢复结果最好，能辨认车牌数字为 4142，但其余信息无法确定，因为此图像除了运动模糊之外，可能还存在光照、大雾等其他因素影响，导致参数估计不准确，且过多的噪声也给图像恢复带来了困难。

图4 运动模糊图像及本文算法、Gabor变换法和频谱分块法的恢复结果

4 结 束 语

准确估计运动模糊方向是恢复运动模糊图像的关键步骤，本文经理论推导，得出了运动模糊方向、图像尺寸和频谱图像中平行条纹方向之间的关系，并提出了基于频谱边缘检测和 Radon变换的估计方法，该方法一方面突出了频谱图像中的暗条纹特征，另一方面减少了频谱图像中的亮十字干扰，使得 Radon变换检测角度更加精确，数值实验部分表明本文的方法不仅适用于任意尺寸的运动模糊图像，而且在其他噪声干扰较小的情况下，对运动模糊图像方向的估计精度更高，但当噪声较大时，频谱图像中的平行暗条纹特征减弱甚至消失，导致 Radon变换无法正确检测角度，因此，有必要进一步分析噪声干扰的情形，继续改进算法使其具有更广泛的应用价值。

[1] Zhao Z H, Zhang L N, Liu X P, et al. A lgorithm for the removing uniformed motion blur [J]. Computer Aided Drafting, Design and Manufacturing, 2014, 24(4): 20-25.

[2] 庞 涛, 程小平. 基于 Radon变换的运动模糊图像参数估计[J]. 科学技术与工程, 2010, 10(22): 5551-5554.

[3] 加春燕, 崔 丽, 黄海洋. Gabor 变换估计模糊角度[J]. 北京师范大学学报, 2009, 44(6): 563-567.

[4] 乐 翔, 程 建, 李 民. 一种改进的基于 Radon 变换的运动模糊图像参数估计方法[J]. 红外与激光工程, 2011, 40(5): 963-969.

[5] 孙兆林. Matlab 6. x 图像处理[M]. 北京: 清华大学出版社, 2002: 132-134.

[6] 加春燕. 运动模糊图像运动长度的频谱估计法[J]. 北京工业职业技术学报, 2015, 14(1): 51-54.

[7] Huang H Y, Jia C Y, Huan Z D. On weak solution for an image denoising-deblurring model [J]. Applied Mathematics, 2009, 24(3): 81-86.

Direction Estimation of Motion Blurred Images Based on Edge Detection of Spectrum and Radon Transform

Jia Chunyan1, Cui Li2

(1. Fundamental Courses Department, Beijing Polytechnic College, Beijing 100042, China; 2. School of Mathematical Sciences, Beijing Normal University, Beijing 100875, China)

To accurately estimate direction of motion blurred images, in the part of theoretical derivation, the relationships among motion blur direction, image size and direction of parallel dark stripes in the spectrum images are derived based on know ledge of definite integral, Fourier transform and the Sinc function. In the part of algorithm optim ization, the principle and deficiency of Radon transform, Gabor transform and spectrum sub–blocks method are analyzed. And then the improved algorithm based on edge detection of spectrum and Radon transform is presented. In the part of numerical experiments, by use of Matlab programs, comparison results of the three methods proved the accuracy of our improved method is the highest, which shows our method is more suitable for estimating direction of motion blurred images.

direction estimation of motion blurred images; edge detection of spectrum images; Radon transform; Gabor transform; spectrum sub-blocks method

O 29

10.11996/JG.j.2095-302X.2016030434

A

2095-302X(2016)03-0434-05

2016-02-26；定稿日期：2016-03-28

国家自然科学基金项目(11001017)

加春燕(1983–)，女，山西临汾人，讲师，硕士。主要研究方向为数学建模、应用数学。E-mail：jiachunyan0@163.com