双排多段排样方式及其生成算法
李 华, 崔耀东, 王严欣
(广西大学计算机与电子信息学院,广西 南宁 530004)
双排多段排样方式及其生成算法
李 华, 崔耀东, 王严欣
(广西大学计算机与电子信息学院,广西 南宁 530004)
为解决大规模矩形毛坯无约束的二维剪切排样问题,提出双排多段排样方式及其生成算法。排样时采用一条剪切线将板材切分为两段,用一组剪切线将每段切分成一系列的块,每个块由一组水平方向的同质条带构成。采用枚举法确定两段分界线的最优位置,通过求解背包模型确定所有可能尺寸的块的最大价值和块在段中的最优布局。利用文献中的2组基准测题对所述算法进行测试,实验结果表明,该算法能在合理的计算时间内取得较好的优化结果。
无约束二维切割;下料;双排多段排样方式;背包问题
矩形件优化排样问题是指将一组矩形件互不重叠的排放在有限的区域内,并实现资源优化利用的布局问题,其研究成果主要应用在板材、玻璃加工业、金属制品业等领域。最大限度的提高材料利用率、节约生产成本、简化切割工艺、缩短计算时间、提高企业效率成为增强企业竞争力的关键。因此,矩形件的优化排样问题一直是国内外众多学者研究的热点。
本文讨论矩形毛坯无约束的二维剪切排样(unconstrained two-dimensional cutting,UTDC)问题:采用剪切方式,将板材长×宽(L×W)切成 m种毛坯,第i种毛坯的尺寸为 li×wi,价值为ci,对每种毛坯在板材出现的次数无约束,排样目标是使得板材所含毛坯的总价值最大。令可行的排样方式P中含第 i种毛坯zi个,N为自然数的集合,则UTDC的数学模型为:

其中:zi∈N;i= 1,…,m;P满足一定的切割工艺的要求。
在生产实践中,经常将UTDC算法和线性规划算法相结合以求解二维下料问题(two-dimensional cutting stock problem,TDCSP)。使用库存板材L×W剪切出 m种矩形小毛坯,第 i种毛坯的尺寸为li×wi,需求量为di,i= 1,…,m,要求确定下料方案,在满足全部毛坯需求的前提下,使得消耗的板材总面积最小。在求解下料方案的过程中,需要反复调用UTDC算法。因此,要求UTDC算法能在合理的计算时间内给出高质量的解。
目前研究的UTDC算法大致可分为3类:①生成普通排样方式的精确算法[1-2];②生成普通排样方式的近似算法[3-4],该算法由于其收敛性未知,无法保证解的质量;③生成具有明确几何性质的排样方式算法,如两段[5-6]、T形[7]、两阶段[8-9]、3阶段[9-10]、层排样[11]、同质三块[12]等排样算法,这类排样算法的利用率可能略低,但其切割工艺简单,在生产实践中仍得到广泛的应用。
文献[5]和[12]均采用递归算法分别生成最优两段布局方式和同质三块布局方式。以上两种布局方式,都是先将板材切分成两段,然后再在段上进行条带的布局排样。另外,在文献[5]的基础上,对文献[12]布局方式添加一条垂直于段分界线的辅助分界线,将板材切分成任意三块。分析以上两种布局方式的几何性质可以得出:两段布局方式⊆同质三块布局方式。故同质三块布局方式理论上的排样价值优于两段布局方式的价值。
本文研究特定类型的排样方式,对文献[12]进行扩展提出双排多段排样方式(double-rows and multi segment,DMS)及其生成算法,即在文献[12]的基础上,将辅助分界线由一条扩展到多条,将板材切成若干块。故理论上DMS排样价值优于三块布局方式的价值是确定的;在切割工艺方面,DMS排样方式还可应用于求解生产中滚剪下料问题,简化切割过程,减少人工工作量。
本文详细介绍了 DMS排样方式及其生成算法,并通过两组实验测题验证了算法的有效性,实验结果将在第 3节详细列出。下文中的叙述表明DMS算法优于经典两段、启发式TABU500算法和同质三块排样算法,且计算时间合理。
1 双排多段排样方式中的概念
在DMS排样方式中,用一条剪切线将板材分为两段,采用若干条辅助分界线将段划分成一系列的块,每个块仅含方向固定的同质条带。下面分别介绍相关概念。
1.1 同质条带
条带由若干个互不重叠、水平(X向)或竖直(Y向)排列的毛坯组成。按照条带所含毛坯类型,可将其分为单毛坯条带和多毛坯条带。单毛坯条带又称同质条带,如图1 (a)所示,其中仅含尺寸和方向均相同的毛坯。多毛坯条带又称普通条带,如图1 (b)所示,其中含多种不同毛坯。本文采用X向同质条带,与采用普通条带相比利用率虽略低,但切割工艺较为简单。

图1 条带
1.2 块
块是指由长度和方向均相同的X向同质条带拼接而成的板材的矩形区域,如图2所示,毛坯中的数字指明毛坯的类型。通过一系列的剪切的过程可将块切分成若干条X向同质条带,每次切下一根X向条带,连续被切下的两根条带相互平行。图2块中包含10号X向条带3根,14号X向条带一根。

图2 块
1.3 段
一个段由一系列的块组合而成,段长度与板材长度或宽度相等。若一系列块从左到右按水平方向排列,则称X向段,如图3 (a)所示;若一系列块自顶向下按竖直方向排列,则称Y向段,如图3 (b)所示。图3中,箭头指示相邻块之间分割线的位置。
1.4 DMS排样方式
DMS排样方式由两排块组成,可分2个阶段将板材切分成一系列块:①将板材切分成两段;②将每段切分成若干个块。图4为DMS排样的两种类型:若两段之间分割线的方向为 X向,称为X-DMS排样,如图4(a)所示,水平箭头指示上下两段分割线的位置,竖直箭头指示相邻块之间剪切线的位置;若两段之间分割线的方向为 Y向,称为Y-DMS排样,如图4(b)所示,竖直箭头指示两段分割线的位置,水平箭头指示相邻块之间剪切线的位置。图4(a)与图4(b)均包含5个块。

图3 段
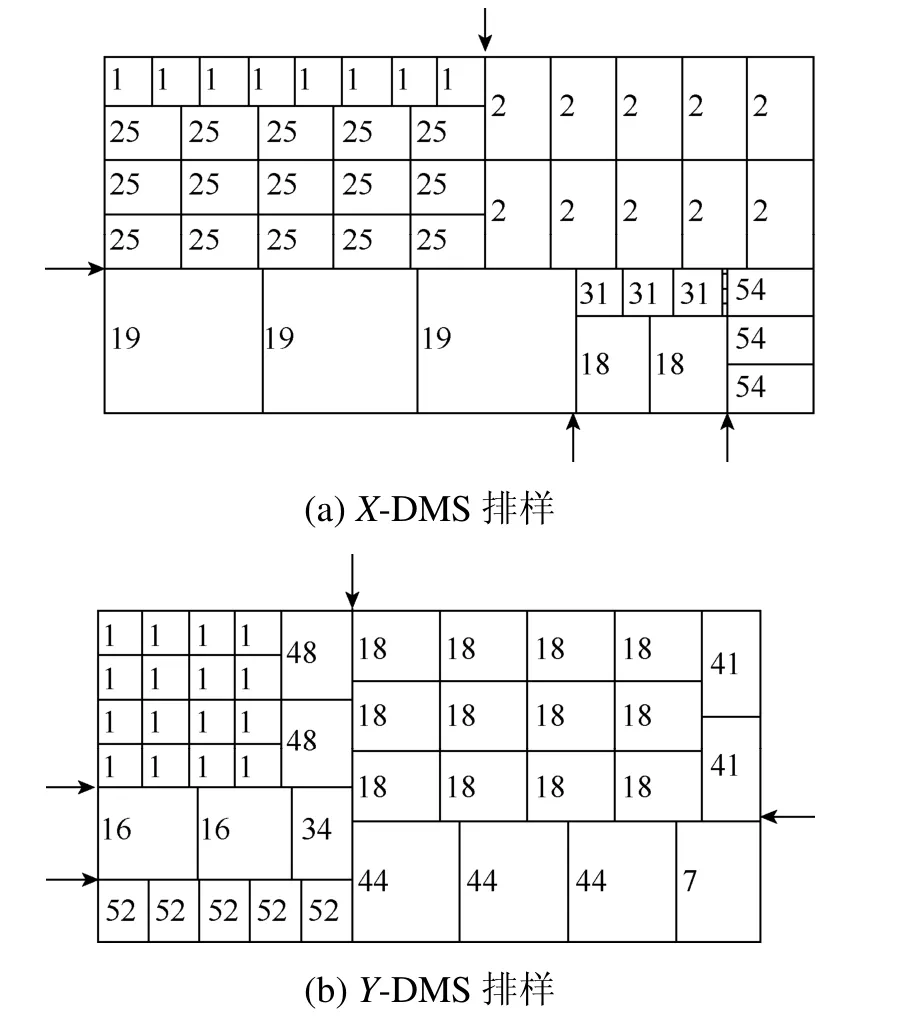
图4 DMS排样方式
2 算法原理及实现
设板材L×W和毛坯的尺寸均为整数,毛坯的方向固定。现只介绍生成X-DMS最优排样的方法,主要包含以下4个步骤:①求解X向带最大价值;②确定不同尺寸的最优块排样;③确定块在段上的最优排样;④生成DMS的最优排样方式。如果同时交换板材的长度与宽度、毛坯的长度与宽度,然后调用X-DMS排样方式算法,就可以生成Y-DMS排样方式。
2.1 求解条带价值
记条带的宽度向量为 W =[w1,w2,…,wm],i=1,…,m,对矩形毛坯li×wi,ci为第i种毛坯的单价,wmin为全部毛坯的最小宽度,即,条带长度为x时的价值向量为,可由如下公式决定:

2.2 生成最优块
对长为x宽为y的块,设含第j种X向带zj根,结合2.1节给出的求解X向带的最大价值方法,根据文献[9]动态规划的算法思想,可确定组成X向段的块中所含条带的总价值 FX(x,y),x≤L,y≤W,递推公式如下:
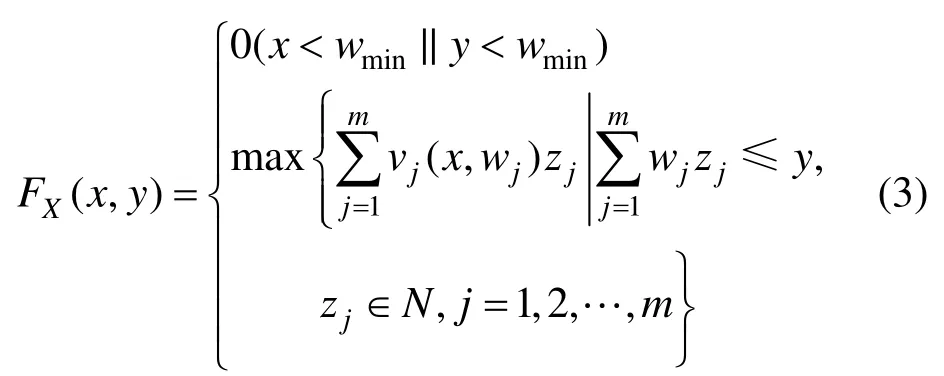
式(3)为最大化一定尺寸块价值的背包问题,可采用文献[13]中的动态规划算法求解。为减少计算时间,在求解过程中利用如下技术减少块中考虑拼接条带的数目:
(1) 将块x×y排样初始化为块 x×(y-1)和块(x-1)×y中较好者。
(2) 若x/wj≤(x-1)/wj,可令zj= 0,因为,当vj(x,wj)出现在块中时,可用较短的条带代替,而不影响解的质量。
2.3 块在段上的最优排样
根据1.3节段的定义可知:X向段由一系列水平排列高度均相同的块构成,记 B(L,Y)为X向段L×Y最大价值,Y=1,…,W,则有如下公式:

上述模型是典型的背包问题,可利用文献[13]中的动态规划算法求解。其中,背包长度为L,需要考虑L种物品,第t个物品的长度为t (对应于尺寸为t×Y的块),该物品个数为ZtY。
2.4 最优DMS方式
设最优X-DMS排样方式的价值为VX-DMS,对应水平分割线的位置为Ymax,则:

2.5 生成DMS方式算法步骤
步骤1.按式(2)确定各种尺寸的条带的价值。
步骤2.按式(3)确定各种尺寸的块的价值。
步骤3.求解式(4),得到各种尺寸的段的价值。
步骤4.按式(5)确定X-DMS排样方式的价值。
步骤5.交换板材的长与宽,交换每种毛坯的长与宽,调用步骤1~4确定Y-DMS排样方式的价值。
步骤6.选取X-DMS和Y-DMS两个排样方式中价值较大者作为最优DMS排样方式。
2.6 算法的时间复杂度
(1) 式(2)确定条带价值的复杂度为 O(mL)。
(2) 式(3)确定块价值FX(x,y)的复杂度为O(mWL)。
(3) 式(4)确定高度一定段价值 B(L,Y)的复杂度为 O(L2W)。
(4) 式(5)确定最优 X-DMS排样价值 Vx-DMS的复杂度为 O(W)。
由于m<<L,综上所述,X-DMS排样算法的时间复杂度为O(L2W),同理可得Y-DMS排样算法的时间复杂度为O(LW2),则DMS算法总的时间复杂度为O(LW(L+W))。
3 实验计算结果
实验所使用计算机为 Pentium(R) Dual-Core CPU,主频3.0 GHz,内存2.0 GB。采用文献中的两组基准测题,将本文DMS算法与多种文献算法相比较。
3.1 第一组基准测题
将 DMS算法与同质条带两段布局算法[5]和同质条带三块布局算法[12]相比较。三者均采用同质条带。采用文献[5]中表4详细描述的6个例题为实验数据,其中板材尺寸3000×1500(单位均为mm),每题 30种毛坯,毛坯的单价和面积相等。计算结果如表 1所示,其中 ID表示题号, VT-2SECTION、VT-3BLOCK和VDMS分别为文献[5]、文献[12]和DMS3种算法所得解值,每题的最好解(解值最大者)以黑体表示。所获得的最好解的数量,对于DMS算法为6个,文献[5]算法为1个,文献[12]算法为2个,说明DMS算法对于提高解的质量最为有效。usage 为 DMS算法所得各题的材料利用率,平均值为99.70%。DMS算法平均每题的计算时间为0.24 s,在实际应用中合理。图5为本文算法生成的测题1的排样方式图。
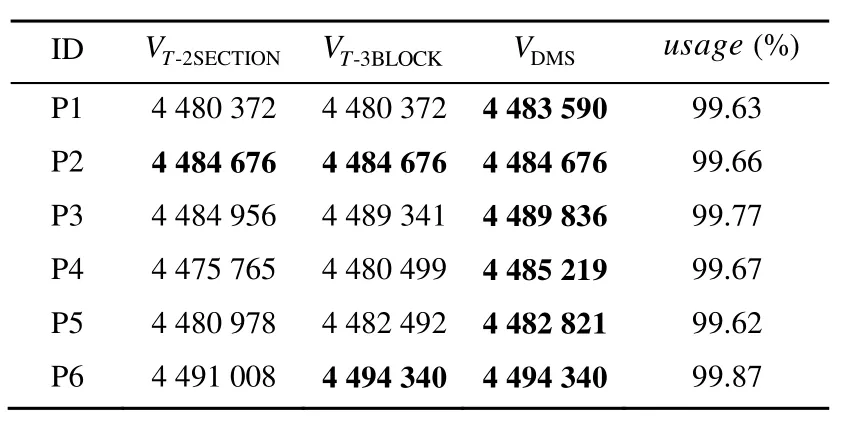
表1 第一组基准测题的实验结果
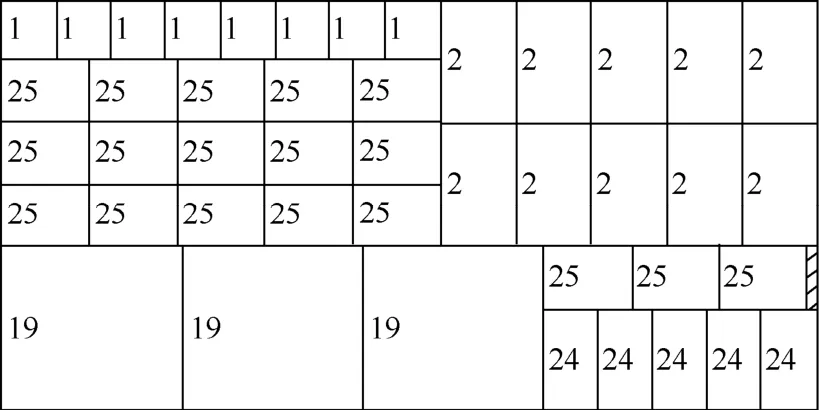
图5 测题1的排样方式图
3.2 第二组基准测题
将DMS算法分别与文献[3]的TABU500和文献[12]的算法相比较。采用文献[3]中表 10报道的20个例题,其中,每题毛坯种数在区间[10,60]中,板材长度和宽度在[1500,3000]中,毛坯长度在[0.05 L,0.4L]中,毛坯宽度在[0.05W,0.4W]中。前10题(APT10-APT19)中,毛坯的价值和面积相等;后10题(APT20-APT29)中,毛坯的价值和面积不相等。具体计算结果如表2所示,其中ID为例题标识,VTABU500、VT-3BLOCK和VDMS分别表示、文献[3]算法、文献[12]算法和DMS算法的解值,每题的最好解以黑体表示。所得最好解的数量,对于 DMS算法为19个,文献[3]算法为5个,文献[12]算法为7个,DMS的求解结果均优于两个对比算法,说明DMS算法对于提高解的质量最为有效。DMS算法平均每题的计算时间为0.39 s,能满足应用需求。图6给出了DMS算法生成的测题APT16和APT22的排样方式图。

表2 第二组基准测题的实验结果

图6 测题APT16和APT22的排样方式图
4 结 束 语
本文提出一种新型特定排样方式——DMS排样方式,并采用DMS算法生成此种排样方式,通过文献测题验证了算法的有效性,证明本文算法总体优于经典两段、TABU500算法和同质三块排样算法。另外,利用该排样方式的特点,下料过程中可充分发挥滚剪机的效率,减少人工操作量。排样过程中采用相关技术减少优化时的搜索空间,在保证有效地提高解的质量前提下,能够满足实际应用对计算时间和切割工艺的要求。将本文DMS算法与线性规划算法相结合,设计求解二维下料问题的算法,可以作为后续研究的内容。
[1] Cui Y D, Zhang X Q. Two-stage general block patterns for the two-dimensional cutting problem [J]. Computers & Operations Research, 2007, 34(10): 2882-2893.
[2] Russo M, Sforza A, Sterle C. An exact dynam ic programm ing algorithm for large-scale unconstrained two-dimensional guillotine cutting problems [J]. Computers & Operations Research, 2014, 50: 97-114.
[3] A lvarez-Valdés R, Parajón A, Tamarit J M. A tabu search algorithm for large-scale guillotine (un) constrained two-dimensional cutting problems [J]. Computers & Operations Research, 2002, 29(7): 925-947.
[4] 李 波, 王 石, 施松新, 等. 基于启发式动态分解算法的矩形件优化排样[J]. 计算机应用, 2013, 33(7): 1908-1911.
[5] Cui Y D, He D L, Song X X. Generating optimal two-section cutting patterns for rectangular blanks [J]. Computers & Operations Research, 2006, 33(6): 1505-1520.
[6] Cui Y D. Heuristic for two-dimensional homogeneous two-segment cutting patterns [J]. Engineering Optimization, 2013, 45(1): 89-105.
[7] 崔耀东. 生成矩形毛坯最优T形排样方式的递归算法[J].计算机辅助设计与图形学学报, 2006, 18(1): 125-127.
[8] Smola A J, Schölkopf B. A tutorial on support vector regression [J]. Statistics and Computing, 2004, 14(3): 199-222.
[9] Cui Y, Huang L, He D. Generating optimal multiple-segment cutting patterns for rectangular blanks [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2004, 218(11): 1483-1490.
[10] Cui Y D. A new dynam ic programm ing procedure for three-staged cutting patterns [J]. Journal of Global Optimization, 2013, 55(2): 349-357.
[11] 王晓庆, 李尚芳, 崔耀东. 矩形毛坯最优层排样方式的动态规划算法[J]. 计算机应用研究, 2010, 27(6): 2040-2067.
[12] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.
[13] Kellerer H, Pferschy U, Pisinger D. Knapsack problems (2004) [M]. Berlin: Springer, 2003, 130-131.
An Algorithm for Generating Patterns of Double-Rows and Multi Segments
Li Hua, Cui Yaodong, Wang Yanxin
(College of Computer and Electronic Information, Guangxi University, Nanning Guangxi 530004, China)
To solve large scale unconstrained two-dimensional guillotine-cutting problem of rectangular items, an algorithm for generating the patterns of double-rows and multi segments is proposed, where the plate is divided into two segments by a cut, each of which is then divided into a series of blocks with a set of cuts, and each block contains a group of horizontal strips. The optimal position of the cut that divides the plate into two segments is determ ined through enumeration. Knapsack problems are solved to obtain the maximum values of all possible blocks and the block layouts on the segments. The algorithm is tested on two groups of benchmark problems in the literature. The computational results indicate that the algorithm can obtain better optimization results in a reasonable computation time.
unconstrained two-dimensional cutting; stock packing; double-rows and multi-segments patterns; knapsack problem
TH 164;TP 301.6
10.11996/JG.j.2095-302X.2016030285
A
2095-302X(2016)03-0285-05
2015-07-07;定稿日期:2016-01-18
国家自然科学基金项目(61363026,71371058);广西自然科学基金项目(2014GXNSFAA118357)
李 华(1986–),女,山东潍坊人,硕士研究生。主要研究方向为智能系统与智能CAD。E-mail:lh401281894@126.com
崔耀东(1957–),男,河南林州人,教授,博士。主要研究方向为智能系统与智能CAD。E-mail:ydcui@263.net

