基于GIS的高架道路交通噪声环评可视化

吴培宁， 周百顺， 周淑秋

(中国劳动关系学院计算机网络应用研究所，北京 100048)

基于GIS的高架道路交通噪声环评可视化

吴培宁， 周百顺， 周淑秋

(中国劳动关系学院计算机网络应用研究所，北京 100048)

针对基于地理信息系统(GIS)的评价区域交通噪声环评可视化问题，引入了基于切割单元法的评价区域网格生成算法，分别提出了基于道路中心线段集的评价区域边界生成方法和基于声照区的网格自适应加密与稀疏算法，实现了复杂评价区域内非结构化网格的生成。在此基础上提出了适应于区域计算的等效声级计算模型，实现了环评计算结果的可视化显示。通过一个高架高速公路的实例，验证了该方法的准确性与有效性。

交通噪声；环评；可视化；地理信息系统

随着城市建设的加快，越来越多的城市高速公路、快速路及主干道采用高架道路的形式。高架道路交通噪声影响评价已成为公路建设项目环评的重要组成部分[1]。基于地理信息系统(geographic information system，GIS)的高架道路噪音环评可视化能够准确直观地分析交通噪声对道路周边声环境的影响，为环评提供基础资料与决策支持，提高其准确性与效率，并且对于高架道路声屏障的规划与建设也具有十分重要的指导意义。

目前，将GIS技术应用于交通噪声的研究已取得了一些进展[2-4]，但主要局限于基于 GIS的道路噪声监测数据可视化分析，以及道路周围离散点的噪声预测。而基于GIS的高架道路评价区域交通噪声环评可视化仍然是一个难点问题，主要体现在：①评价区域边界确定与网格剖分问题。对于复杂高架道路系统，其评价区域是位于道路两侧的两个复杂多边形。由规划道路的中心线段集来确定评价区域多边形的边界，生成评价区域边界线段集并完成网格剖分是一个非常复杂的问题；②与一般道路不同，高架道路的桥面一般采用钢筋砼做支柱，桥面距评价区域地面有几十米的高度。其桥面道路两侧边缘有垂直于路面的路侧防撞护栏，且按照国家环境污染防治法的相关规定，经过噪声敏感建筑集中区域的高架道路还需设置声屏障。因此，高架道路评价区域内有大片区域属于声影区。而现有环评导则计算模式中声影区的计算仅适用于点计算，无法满足区域环评计算的要求；③环评计算结果的可视化显示问题。

针对基于GIS的高架道路交通噪声环评可视化难点①，本文提出了基于切割单元法的评价区域非结构化笛卡尔网格生成方法。切割单元法是一种近年来发展起来的二维复杂区域网格剖分方法，其基本思想是采用笛卡尔背景网格与区域轮廓线求交以得到切割单元网格及轮廓线内网格[5-6]。该方法应用于大气及水环境GIS环评可视化中取得了良好的效果[7-9]，结合自适应分层切片算法后也可应用于三维复杂形体的网格剖分与物理场可视化[10-11]。

针对难点②，本文提出了适用于区域计算的声影区及声照区等效声级计算模型。针对难点③，本文采用了基于非结构化笛卡尔网格的噪声等效声级等值线生成方法。

应用上述方法开发了基于GIS的环评可视化系统，首次实现了高架道路交通噪声评价区域内的GIS环评可视化。

1 基于切割单元法的评价区域网格生成

1.1 高架道路噪声评价区域确定

依据声环境影响评价技术导则[12]，在公路建设项目声环境影响评价中，为满足一级评价的要求，一般以道路中心线外两侧200 m以内为评价范围，如依据建设项目声源计算得到的贡献值到 200 m处，仍不能满足相应功能区标准值时，应将评价范围扩大到满足标准值的距离。本文的研究对象为高架高速公路及主干道路，因其道路宽阔、交通流量大且沿线敏感目标多，因此其评价区域确定为：

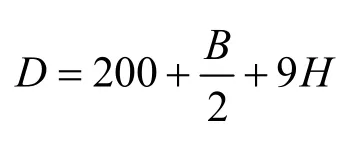
其中，D为道路中心线至评价区域一侧边界的垂直距离(单位为m)；B为道路宽度；H为高架道路的高度。

在GIS系统中，规划建设的公路项目由一组折线段构成，其线段集表示为：

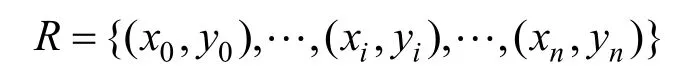
其中，R为规划公路的道路中心线段集；(xi, yi)为某一道路中心线段的端点。

该公路项目的声环境评价区域为沿道路两侧的两个封闭区域，如图1所示，其任一封闭区域的内边界为道路一侧边沿，外边界为距道路中心线D的一组折线段集。沿道路中心线前进方向，其道路左侧及右侧边界线段集由Rl及Rr表示，评价区域边界线段集由RL及RR表示。则：

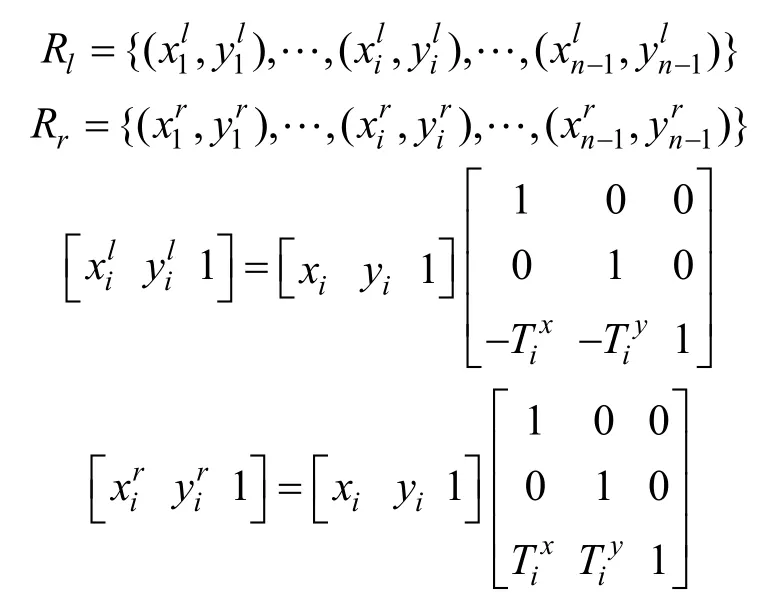
其中，αi为第i段道路中心线段与X轴的夹角。

沿顺时针方向排列的公路左侧评价区域边界线端点集由 CL表示，右侧评价区域边界线端点集由CR表示。

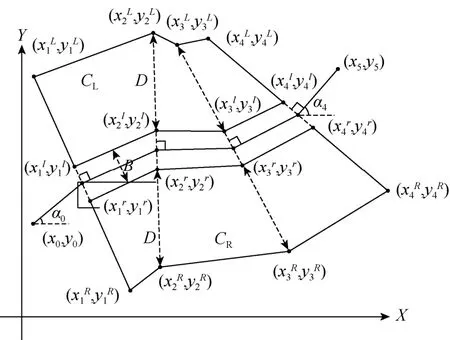
图1 高架道路噪音评价区域

1.2 切割单元交点追踪与背景网格单元删除

基于笛卡尔切割单元法的交通噪声环评计算网格生成过程是：采用背景网格与评价区域封闭边界折线集CL与CR中的每一条边界线段逐一求交，其结果由评价区域内网格单元与边界切割网格单元组成。在切割过程中，如图2所示CL中评价区域左侧边界线中某一线段由起点坐标与终点坐标确定，包含该线段起点与终点的背景网格单元(Is, Js)及(Ie, Je)为：

其中，int(x)表示对x的取整；x0、y0为计算区域左下角处的坐标；Δx与Δy为背景网格在X轴与Y轴方向的间距。

该边界线段与背景网格单元的交点a、b、c、d、e可依据切割单元交点追踪算法获得[5-6,10-11]。

图2 道路线段切割点的追踪

在进行切割单元交点追踪前，先将背景网格单元标记为初始网格单元，当完成所有切割单元的交点追踪后，则将所有与评价区域边界折线集有交点的初始网格单元标记为切割网格单元，存入切割单元链表中。

完成背景网格与噪声评价区域边界线的切割后，背景网格被分成3类：①评价区域内网格；②评价区域外网格；③边界线切割网格。评价区域外网格作为无用网格需要加以删除。

在删除无用网格过程中，首先需要判断哪些背景网格节点被评价区域边界线包围。如采用常用的点与多边形包含关系判断算法，则对于评价区域边界线为凹多边形且折线段数量巨大的情况，存在着判断不准确及效率低下的缺点。因此，本文采用了基于凸包的点集与多边形包含关系判断方法[13]来判断背景网格节点与评价区域边界线之间的包含关系。通过计算背景网格节点集的凸包[14]，得到被评价区域边界线包围的背景网格节点集，并将除该节点集以外的背景网格删除。算法的时间复杂度为：

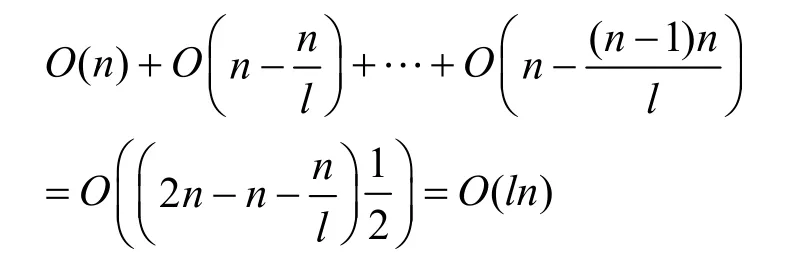
远低于点与多边形包含关系判断算法的时间复杂度O(mn)，因此在得到被评价区域边界线包围的背景网格节点集时节省了大量的计算时间。

1.3 碎片切割单元的合并

通过笛卡尔切割单元法得到的公路噪声环评计算网格由评价区域内网格单元与边界切割网格单元组成，但当某一个切割单元过于细小时，将降低环评计算与可视化显示的效率。如图 3(a)所示，灰色部分为评价区域内，评价区域边界线段a及a+1与背景网格切割后共得到12个切割单元，其中单元j、q为碎片单元。需采用碎片切割单元合并算法将其与相邻切割单元合并。通过切割单元的合并得到如图3(b)所示合并后的切割单元k、r。合并算法如下：

步骤1. 对于CL与CR两个评价区域，分别从端点开始，顺序遍历各评价区域的切割单元链表，判断每一个切割单元的节点数，若节点数等于4则不需要被合并，直接进入步骤4。

步骤2. 对于节点数小于4的切割单元，计算其沿边界线方向两个切割点间线段长度及两个切割点与另一单元节点的距离。若3个长度值中有一个值小于合并阈值，则判定此为碎片单元。如图3(a)所示，切割单元j与q的某一个长度值小于合并阈值，则判定为碎片单元。

步骤 3. 当碎片切割单元被确定后，将其与下一切割单元k、r合并，作为一个单元存入合并单元链表中。

步骤4. 对下一个切割单元执行步骤1的判断，直至完成对切割单元链表的遍历。

以上算法的时间复杂度为O(n)。

图3 碎片切割单元的合并

完成碎片切割单元的合并后，边界切割网格单元存储于合并单元链表中。该链表为双向链表，其数据域由下式描述：

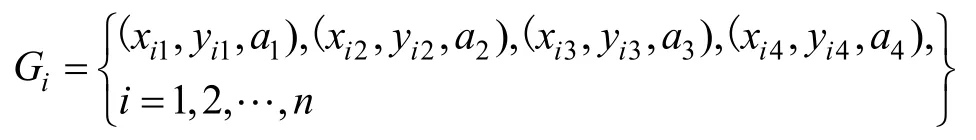
其中， (xi1,yi1),(xi2,yi2),(xi3,yi3),(xi4,yi4)为边界切割单元4个节点坐标； (a1,a2,a3,a4)为节点属性，其属性分为边界线段切割交点与背景网格点两类。

如图4所示，噪声环评计算网格包括评价区域内网格单元与边界切割网格单元，分别存储于左侧评价区域内网格单元链表、左侧评价区域合并单元链表、右侧评价区域内网格单元链表和右侧评价区域合并单元链表中。

图4 切割单元法得到的评价区域网格

2 高架道路交通噪声预测模型

2.1 高架道路噪音预测模型

依据声环境影响评价技术导则[12]，某型车等效声级的预测计算为：

其中，Leq(h)i为第i类车的小时等效声级，单位为dB(A)；Ni为昼间、夜间通过某个预测点的第i类车平均小时车流量，单位为辆/小时；r为从车道中心线到预测点的距离，单位为m；Vi为第i类车的平均车速，单位为km/h；T为计算等效声级的时间，单位为h；1ψ、2ψ为预测点P到有限长度公里线段A、B两端点的张角，单位为弧度(如图5所示)；ΔL为由其他因素引起的修正量，单位为dB(A)；ΔL d的计算为：

将高架道路的公路纵坡坡度设为0°，路面类型为沥青混凝土，则：

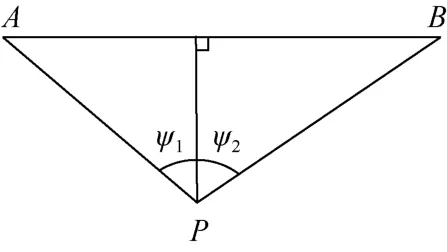
图5 有限路段的修正

则高架公路总车流等效声级为：

其中，Leq(h)大、Leq(h)中、Leq(h)小分别为大型车、中型车及小型车的小时等效声级，单位为dB(A)；ΔL1为线路因素引起的修正量；ΔL坡度为公路纵坡修正量；ΔL路面为公路路面材料引起的修正量；ΔL2为声波传播途径中引起的衰减量；ΔL3为由反射等引起的修正量，单位为dB(A)。

2.2 声波传播途径修正量及衰减量计算

在声波传播途径引起的衰减量ΔL2计算中，需要计算大气吸收引起的衰减量Aatm、地面效应衰减量Agr、屏障引起的衰减量Abar及其他多方面引起的衰减量Amisc。

大气吸收衰减量Aatm为：

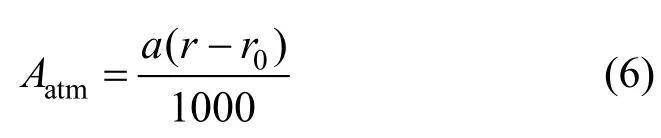
其中，a为大气吸收衰减系数，预测计算中可由项目所处区域常年平均气温和湿度查表选择相应的值，单位为dB/km；r为预测点至声源的距离，单位为m；r0为某一通过实测已知声级的参考点至声源的距离，单位为m。

地面效应衰减量Agr为：

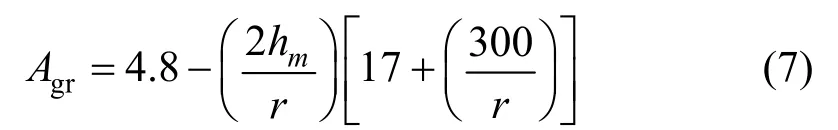
其中，r为预测点至声源的距离，单位为m；hm为传播路径的平均离地高度，单位为m。

屏障引起的衰减量Abar是指高架道路高路堤或低路堑两侧声影区的衰减量，高路堤或低路堑两侧声影区衰减量Abar为预测点在高路堤或低路堑两侧声影区内引起的附加衰减量。如图6所示，声源点离路面高度为1 m，路面距地面高度为H，接受点离地面高度为h。当预测点处于声照区时，Abar为零。当预测点处于声影区时，Abar取决于声程差，声程差δ=a+b–c。

图6 声程差计算示意图

在目前环评计算中，需要依据δ值根据500 Hz时的噪声衰减量Abar与声程差δ关系曲线图来人工确定Abar的值，无法满足区域环评计算的需要。因此本文采用最小二乘法进行曲线拟合，将该关系曲线图拟合为四段直线，以满足评价区域内接受点集的屏障衰减量Abar自动计算需求。将声程差δ划分为0.01～0.10 m、0.10～1.00 m、1.00～10.00 m、10.00～100.00 m 4个区段，每区段10个点，根据这40个声程差δ值，可查得40个衰减量Abar值，每一区段10个值。4个区段集合分别为：

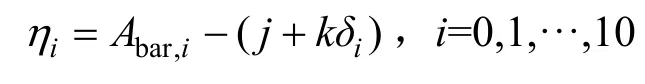
将i个误差平方后加起来得到总误差：

由下列方程组所决定：

解之则有：

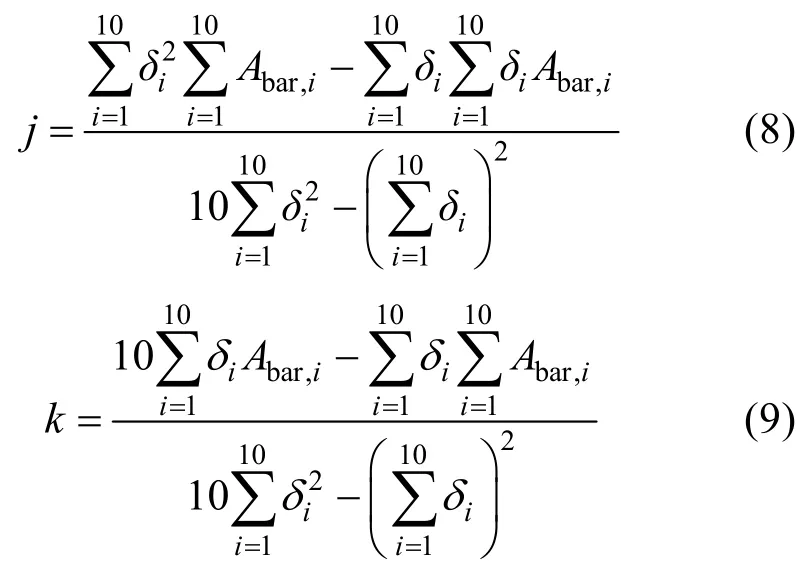
将每一区段中的δ值与Abar值代入式(8)、(9)，可求得该区段相应的j、k。则S1、S2、S3、S4区段衰减量Abar的最小二乘法拟合公式分别为：

当接受点位于声照区时，屏障引起的衰减量Abar为零。当接受点位于声影区时，需首先计算声程差δ，根据计算得到的δ确定该接受点的Abar所属区段，再根据该区段的衰减量最小二乘法拟合公式代入δ值后求出Abar。

2.3 评价区域内非结构化笛卡尔网格生成

在高架道路噪声环评数值模拟中，其车流等效声级大小与车辆种类、车流量、气象条件、高架桥土木结构、路堤高度及声屏障遮蔽角等诸多环评参数密切相关。而切割单元法生成的评价区域内网格为结构化笛卡尔网格，其网格间距等于背景网格的间距。将固定间距的结构化笛卡尔网格应用于不同环评参数的噪声计算，无法兼顾数值计算及可视化显示的精度与效率。若减小背景网格间距将造成切割单元交点追踪计算量的增大及碎片切割单元数目的增加，而增加背景网格间距又会降低计算精度。

针对这种情况本文提出了基于声照区的网格自适应加密与稀疏算法，对通过切割单元法得到的评价区域内网格进行局部加密或稀疏，生成非结构化笛卡尔网格，以兼顾环评计算及可视化的准确性与效率。具体算法如下：

步骤 1. 人机交互输入环评参数，包括：高架道路高度、宽度、路面类型、路肩高度、接受点高度、设计时速、各类车型平均小时车流量、项目所处区域常年平均气温和湿度等相关参数，将输入的相关参数存入环评参数表中。

步骤 2. 依据输入的环评参数计算得到声影区长度L声影，沿道路中心线前进方向，其公路左侧及右侧声影线段集由SRL及SRR表示。则：

沿顺时针方向排列的公路左侧声影区域边界线端点集由SCL表示，右侧声影区域边界线端点集由SCR表示，即：

步骤3. 判断被SCL与SCR包围的网格节点，将其从所属链表中删除，存储于新的链表中。将噪声环评计算网格更新为声影区域内网格单元与边界切割网格单元及声照区域内网格单元与边界切割网格单元。分别存储于左、右侧声影区域内网格单元链表；左、右侧声照区域内网格单元链表；左、右侧声影区域合并单元链表；左、右侧声照区域合并单元链表中。

步骤 4. 在左侧及右侧声照区域内距声影线最近处选取一个检测单元，依据输入的环评参数计算检测网格单元4个节点的噪声值，在每一个检测单元内，计算4个节点间的噪声等效声级值差，并进行计算：

其中，ΔLeq为检测单元各节点等效声级值差的最大值；Δ1,2，Δ2,3，Δ3,4，Δ1,4，Δ1,3，Δ2,4为检测单元节点间的等效声级值差。

步骤5. 根据求得的ΔLeq来分别判断是否对左侧及右侧声照区域内网格网格单元进行加密或稀疏。若 ΔLeq大于加密阈值，则进行加密。若 ΔLeq小于稀疏阈值，则对该声照区域内网格单元进行稀疏。若不满足上述条件，则网格间距不变。

步骤6. 若进行了网格加密或稀疏，则更新左、右侧声照区域内网格单元链表，将加密或稀疏后的网格单元存入左、右侧声照区域内网格单元链表。

以上算法的时间复杂度为O(lmn)。图7所示为对左、右侧声照区内网格单元进行一次加密后的网格单元。

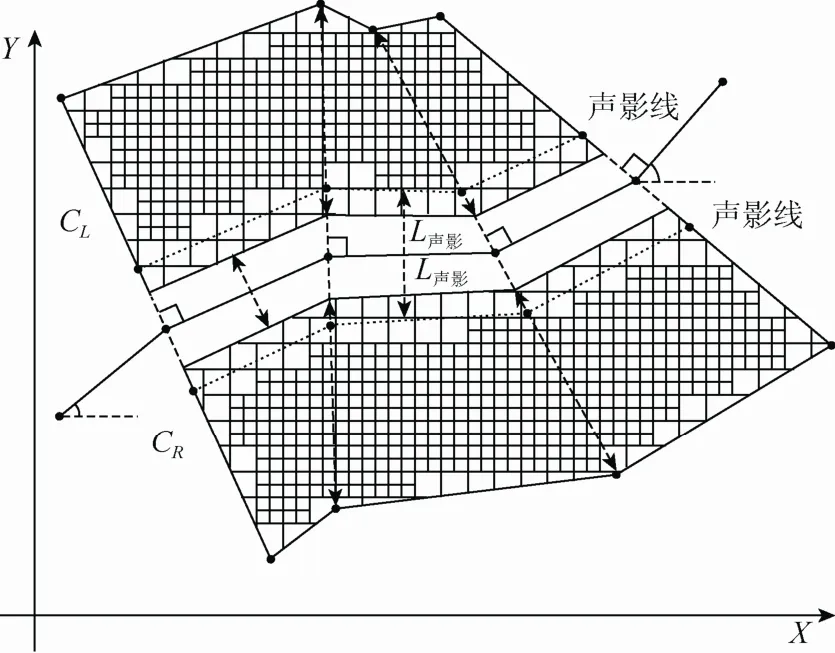
图7 评价区域内非结构化笛卡尔网格

2.4 评价区域交通噪声预测算法

评价区域内网格的生成，使区域交通噪声环评计算成为可能。对于左侧及右侧评价区域内网格，需要按照其所属区域，分别采用声照区及声影区等效声级计算公式，求得其噪声值。以左侧评价区域为例，其算法如下：

步骤 1. 依次遍历左侧声照区域内网格单元链表、左侧声照区域合并单元链表、左侧声影区域内网格单元链表及左侧声影区域合并单元链表。

步骤2. 对于被遍历网格单元中的任一节点P，从该点依次向规划公路道路中心线段集R中的公路线段做垂线。若垂线与该线段有交点，则此线段为P点的影响路段，P点与交点的距离则为预测点至声源的距离 r。P点与影响路段两端点的夹角即为张角ψ1与ψ2。

步骤3. 读取环评参数表中已交互输入的参数，若 P点为声影区网格节点，则计算其声程差δ，根据δ确定P点的Abar所属区段，由式(8)～(11)中的某式得到Abar值。若P点为声照区网格节点，则其Abar值为零。再由式(6)、(7)求得Aatm与Agr，共同代入式(2)得到ΔL。将ψ1、ψ2及ΔL代入式(1)求得第i类车的小时等效声级 Leq(h)i。

步骤4. 由式(5)得到影响路段对P点的总车流等效声级，若P点有多条影响路段，则其总车流等效声级 Leq为各影响路段等效声级的代数和。将计算结果存入左侧评价区域噪声值链表中。

步骤5. 对下一个网格节点执行步骤1，直至完成对所有单元链表的遍历。

以上算法的时间复杂度为 O(4mn2)，将该算法分别应用于左、右侧评价区域，生成左侧及右侧评价区域的两个噪声值链表，就实现了整个评价区域内噪声等效声级的计算。

3 可视化与实例分析

3.1 基于非结构化笛卡尔网格的噪音等值线生成

左侧及右侧评价区域两个噪声值链表的生成为噪声等值线的绘制提供了数据基础，该链表为双向链表，其结点数据域描述为：

其中，(xi,yi)为网格节点Vi坐标；为 Vi节点沿X轴、Y轴正向及负向至相邻网格节点的距离；Leq为Vi节点处的总车流等效声级。

二维标量场等值线抽取方法分为网格序列法与网格无关法两大类，网格无关法适用于等值线分布较规则，且穿过的单元数只占整个网格单元的较小部分(10%以下)的情况。网格序列法适用面较广，但对于四边形网格马鞍点二义性的解决很复杂。目前常用的等值线抽取算法主要是网格序列法，采用的网格大多为矩形网格或三角形网格，但这类算法均无法适用于非结构化各项异性笛卡尔网格数据场。

本文针对评价区域内噪声等效声级值的分布特点，采用了基于非结构化各项异性笛卡尔网格的等值点追踪算法及等值点连接算法[10]，两个算法的时间复杂度均为O(n)。

完成等值点的追踪与连接后的等值线数据存储于GIS系统的TAB表中，将其依次连接后等到的等值线是由多条线段构成，颜色为单色。对于非结构化各向异性笛卡尔网格，由于其网格单元尺寸差异很大，在大网格单元区域会出现锯齿状等值线，且单色等值线集无法直观反映评价区域内噪声变化情况。

因此需采用等值线光滑与颜色映射算法[10]，对等值线进行后续处理并在GIS系统中完成可视化。步骤如下：

步骤1. 读取等值线数据TAB表，采用三次样条函数对等值线进行光滑，将求得的插值点坐标存入光滑等值线TAB表中。

步骤2. 建立基于噪声等效声级值的颜色映射表，依据每条等值线的等效声级dB(A)通过颜色渐变算法赋予其颜色R、G、B值。

步骤3. 在GIS中创建一个图层，读取光滑等值线TAB表，将插值点采用给定颜色R、G、B值的直线段依次连接起来，绘制得到经三次样条函数光滑的等值线。

步骤4. 将绘制完成的等值线图层与背景地图叠加显示，实现基于GIS的噪声环评可视化。

3.2 系统实现

采用本文提出的方法，在Mapinfo平台上实现了高架道路交通噪声的环评计算及可视化。图8所示为评价区域内等效声级等值线与背景地图叠加显示图，其高架道路中心线的前进方向为自右下向左上，中心线至评价区域一侧边界的垂直距离D为350 m，图中下部为左侧评价区域，上部为右侧评价区域。评价区域内共有9条等值线，按评价导则要求设等值线间隔为5 dB(A)[12]，每条等值线的等效声级值均在屏幕上输出。依据国家声环境质量标准[15]，评价区域为4a类，其昼间噪声等效声级限值为70 dB(A)。因此大于等于70 dB(A)的等值线，其颜色随等效声级值升高而渐变至红色，小于70 dB(A)的等值线其颜色保持系统默认色。

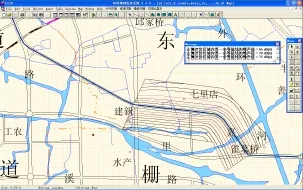
图8 评价区域内噪声等效声级等值线与背景地图叠加显示

3.3 实例分析

为验证本系统对于评价区域噪声环评计算的准确性，将其计算结果与噪声实测数据进行了比较。实验地点选择在G6高速公路官厅湖特大桥，选择此实验地点的原因是其地理环境优越，测量场地开阔、无任何反射物，且G6高速车流量大，车型以大型车为主。大桥桥面至地面高度为20.5 m、桥面宽27 m、中央分隔带宽带1 m、桥长1 846 m、路侧防撞护栏高0.5 m，路面材料为沥青混凝土。所使用声级计为宏城科技 HT-8352，风速与风温计为HT-856C，测量时风向为北风，平均风速为3.6 m/s，满足声环境质量标准要求[15]。测量时间为昼间，声级计距地面高度1.2 m。长度测量采用HT-308激光测距仪及JY-361999测距轮，在与桥梁路面边界线水平距离65 m、100 m、200 m、300 m处分别设置4个噪声监测点。4个监测点同步进行测量，每次测量时间为30 min，并同时监测车流量。左侧评价区域环评计算与监测结果对比如表1所示。

表1 GIS噪声环评计算与实际监测结果比较

表中数据显示 GIS环评系统所计算的噪声预测值与实测值基本相近但存在一个下偏差，其原因在于：系统在计算地面效应衰减时是按疏松地面由式(7)求得Agr值。而监测点位于官厅水库岸边，预测点接收到的部分声波其声源区及中间区域为水面。水面属于坚实地面，其地面因子G为0，而疏松地面的地面因子G为1[16]，此差异导致预测值低于监测值。

距离声源最近的65 m处监测点，其值较低是因为此处位于声影区，其δ值为0.48 m，代入式(9)得到屏障引起的衰减量Abar为11.155 dB(A)。100 m处监测点对于最外侧车道来说已处于声照区，因此此处的等级声效值比65 m处有了大幅增加。

4 结 束 语

本文引入基于切割单元法的高架道路噪声评价区域网格生成方法，结合声照区网格自适应加密与稀疏算法，对通过切割单元法得到的评价区域内网格进行局部加密或稀疏，生成非结构化笛卡尔网格，提高了环评计算的准确性与效率。针对现有环评导则计算模式仅适用于点计算，无法满足区域环评计算的问题，对声程差δ与噪声衰减量Abar关系图进行了曲线拟合，实现了声影区的区域计算。首次实现了基于GIS的高架道路评价区域交通噪声环评可视化。通过案例分析，验证了文中所提方法的准确性与有效性。实验表明，基于GIS的环评可视化系统在声环境影响评价中有着良好的应用前景。而如何将本文所提方法由二维扩展至三维，更好地反映交通噪声的时空分布特征则是下一步的研究重点。

[1] 盖 磊, 王亚平. 快速高架复合道路近场交通噪声垂向分布[J]. 环境工程学报, 2014, 8(4): 1687-1691.

[2] 王建华, 赵江华, 秦其明, 等. 道路噪声预测的GIS评价方法[J]. 测绘科学, 2015, 40(2): 128-131.

[3] 陈冬青, 袁晓梅, 施月娣. 基于GIS的交通噪声综合评价系统研究[J]. 工程图学学报, 2007, 28(5): 136-141.

[4] 黄宝香. 基于VRGIS的城市噪声三维分析模型及可视化评价研究[D]. 青岛: 中国海洋大学, 2011.

[5] Ingram D M, Causon D M, Mingham C G. Developments in Cartesian cut cell methods [J]. Mathematics and Computers in Simulation, 2003, 61(3-6): 561-572.

[6] Gao F, Ingram D M, Mingham C G. The development of a Cartesian cut cell method for incompressible viscous flows [J]. International Journal for Numerical Methods in Fluids, 2007, 54(9): 1033-1053.

[7] 吴培宁, 赵 越, 孙晓霞. GIS环评可视化的自适应图像处理方法[J]. 计算机工程, 2008, 34(12): 271-273.

[8] 吴培宁, 谭建荣, 刘振宇, 等. 基于 Voronoi图的环评等值线快速拓扑填充[J]. 浙江大学学报: 工学版, 2009, 43(2): 321-327.

[9] 吴培宁. 基于笛卡尔切割单元法的复杂河道地理信息系统环评可视化[J]. 计算机应用, 2014, 34(3): 780-784. [10] 吴培宁. 基于变层厚的复杂区域物理场可视化若干关键技术研究及其应用[D]. 杭州: 浙江大学, 2006.

[11] Wu P N, Tan J R, Liu Z Y. Adaptive layered Cartesian cut cell method for the unstructured hexahedral grids generation [J]. Chinese Journal of Mechanical Engineeing, 2007, 20(2): 6-12.

[12] 中华人民共和国环境保护部. HJ2.4—2009 环境影响评价技术导则—声环境[S]. 北京: 中国环境科学出版社, 2009.

[13] 周培德. 判断点集是否在多边形内部的算法[J]. 计算机研究与发展, 1997, 34(9): 672-674.

[14] Ye Q Z. A fast algorithm for convex hull extraction in 2D images [J]. Pattern Recognition Letters, 1995, 16: 531-537.

[15] 中华人民共和国环境保护部, 国家质量监督检验检疫局. GB3096—2008声环境质量标准[S]. 北京: 中国环境科学出版社, 2008.

[16] 国家技术监督局. GB/T 17247.2—1998声学户外声传播的衰减 第2部分: 一般计算方法[S]. 北京: 中国标准出版社, 1998.

GIS-Based EIA Visualization of Elevated Road Traffic Noise

Wu Peining, Zhou Baishun, Zhou Shuqiu

(Institute of Computer & Network, China Institute of Industrial Relations, Beijing 100048, China)

Focus on the visualization of GIS-based evaluation area traffic noise environmental impact assessment (EIA), the boundary lines generating algorithm followed on the centre line of the road is presented. A method for the Cartesian grids generation with sound area self-adaptive grids refinement algorithm is provided to the complex evaluation area for the unstructured grids generation. Based on the unstructured grids, the equivalent sound level EIA model for evaluation area is proposed and the visualization of the EIA calculation is achieved. Through the visualization and analysis of an elevated highway example, the accuracy and efficiency of the proposed methods are confirmed.

traffic noise; environmental impact assessment; visualization; geographic information system

TP 391.9

10.11996/JG.j.2095-302X.2016030308

A

2095-302X(2016)03-0308-08

2015-11-02；定稿日期：2015-12-10

中国劳动关系学院院级科研项目(一般项目15YY002)

吴培宁(1966–)，男，北京人，副教授，博士。主要研究方向为可视计算与图形学。E-mail：wupeining@ciir.edu.cn