一类级数部分和不等式及其应用
罗静
(四川理工学院理学院, 四川自贡643000)
一类级数部分和不等式及其应用
罗静
(四川理工学院理学院, 四川自贡643000)
级数部分和不等式是不等式研究和近代数学发展的基础,基于对经典不等式的研究,建立了一类含有多个参数,结构形式简洁的级数部分和不等式。应用基本不等式,结合初等变换对所建立的不等式进行了严格证明。在分析该类不等式结构特征的基础上,赋于参数特定的值式,得出了一系列重要的推论。通过实例,检验定理及其推论在构造或者证明一大批级数部分和不等式中具有普适性。同时所得结果不仅囊括了众多著名不等式,更是对这些不等式以及相关文献结果的推广、改进和加强。
基本不等式;级数部分和不等式;普适性
引言
级数部分和不等式在不等式研究中占有重要地位,它的一些著名定理在很多领域都是重要的基本工具,是近代数学发展不可缺少的理论基础(比如经典的Holder不等式和Minkowski不等式是建立Lp空间的基本工具)。本文以几个基本不等式为引理,建立了一类很有意义的级数部分和不等式。这些结果推广或改进了相关文献的相应结果,在不等式研究中有较好的应用。
1基本引理
引理1(Jensen不等式推论)设xk>0(k=1,2,…,n),当p≤0或p≥1时,
(1)
当0 (2) 当p=0,或p=1,或x1=x2=…=xn时等号成立。 注在文献[1]中取f(x)=xp(x>0)即得此推论。 引理2(cp不等式)设xk>0(k=1,2,…n),当p≤1时, (3) 当p>1时, (4) 当p=1,或n=1时等号成立。 引理3(Holder不等式)设xk,yk≥0(1≤k≤n),α+β=1,当αβ>0时, (5) 当αβ<0时, (6) 引理4(Chebyshev不等式)设{xn},{yn}是两个实序列,当它们同增,或同减时, (7) 当它们一增一减时, (8) 当且仅当x1=x2=…=xn,或y1=y2=…=yn时等号成立。 定理1设xk,yk>0(1≤k≤n),r>0,则当αβ<0,α-β≥r时, (9) 当αβ>0,α-β≤r时, 即是 同理可证αβ>0, αβ≤r时的情况。 定理2设xk,yk>0(1≤k≤n),r>0,αβ>0,α-β≥r,则 即是 定理3设xk,yk>0(1≤k≤n),r>0,α>0,β<0,α-β≤r,则 证明同定理2,过程略。 定理4设xk,yk>0(1≤k≤n),r>0,则 当α≤0,β>0时有 (10) 当α≥0,r≥-β>0时,不等号反向。当且仅当x1=x2=…=xn,且y1=y2=…=yn时等号成立。 即(10)式成立。 (ⅱ)当α<0,β>0时,由(ⅰ)的结论得 式两边β-α乘方后取倒数得 由传递性得 此时(10)式成立。 同理可证α≥0,r≥-β>0时的情况。 定理5设xk,yk>0(1≤k≤n),α≥r>0,若β>0,且{xn},{yn}是一增一减序列,或β≤-r,且{xn},{yn}是同增或同减序列,则 当x1=x2=…=xn,且y1=y2=…=yn,或α=β,且xk=λyk(λ为常数)时等号成立。 即是 同理可证β≤-r,且{xn},{yn}是同增或同减序列的情况。 当x1=x2=…=xn,且y1=y2=…=yn,或当α=β,且xk=λyk(λ为常数)时等号成立。 证明同定理5,过程略。 在定理1~定理6中,各不等式成立的条件虽然各异,但结果的结构形式相同或者十分相近。特别是指数α与β的非共轭性,寓示着不等式有较宽的应用范围。对定理中各参数取适当的值可得出一系列重要的推论。 在定理2,定理3和定理4中,取yk=1,即得此推论。特别,取r=1,即为引理1。 在定理1中,设β=-α<0,即得此推论。特别,取α=1,r=2,即是Cauchy不等式。 在定理1中,设α=p,β=-q,r=1,即得此推广。 推论5(Radon不等式推广)设xk,yk>0(1≤k≤n),则当p>0,q<0,p+q>0时, 当p>0,q>0时, 在定理1中,设α=p+q>0,β=q<0,r=p得推论5中第一个不等式,设α=p+q,β=p>0,r=q>0得推论5中第二个不等式。特别,在第二个不等式中取q=1,即是Radon不等式。 在定理5与定理6中,设β=-α即得此推论。特别,若取α=r=1,则得文献[2]中的不等式。 推论8 (Minkowshi不等式推广)[5-8]设ajk>0(1≤k≤n,1≤j≤m),则当p≥1时, 当p≤1时,不等号反向。当且仅当 等号成立。 记 则 依次取j=1,2,…,m得m个同向不等式,累加得 即 得 同理可证p≤1时的情况。特别,当m=2时即为Minkowshi不等式。 证明在定理4中取r=1,α=q≤0,β=p>0,设xk=bk,yk=ak,(或在定理2中取r=1,α=q,β=p>0使q-p≥1,设xk=bk,yk=ak),则有 所以不等式成立。 证明在定理2,定理4中取α=2p(p≥1,或p≤0),β=r=1,则有: 证毕。 特别,在此命题中,设A=t=β=1,B=-1,bk=xk,ck=xk+1,则得文献[9]中的不等式: 若再取p=1,则得文献[10]中的不等式: 证明(ⅰ)当p>0时,文献[11]已证不等式成立。 (ⅱ)当p≤0时,在定理4中,取α=p≤0,r=β=1,则 设xk=ak,yk=M-ak,得 综合(ⅰ)与(ⅱ),对∀p∈R,不等式成立。 特别,若取p=M=1,则为Shapiro不等式。 证明当p>1,q<0,且p+q≥1时,根据推论4得: ∑ak(ak+bk)p≥ 同理, ∑bk(ak+bk)p≥ 两式相加: ∑(ak+bk)p+1≥ 所以, 即 例5(Mikolas不等式)设ajk>0,若β≥1且αβ≥1,则 当β≤1且αβ≤1时,不等式反向。 两边β方, (11) 所以待证不等式左式成立。又根据推论8,当β≥1时, 所以, 所以, (12) 即待证不等式右式成立。综合(11)式与(12)式,命题获证。 同理可证β≤1且αβ≤1的情况。 本文定理所述不等式结构特征具有简单性和普适性[12],如果继续对其中各量取适当的值式,不仅可以涵盖、推广或改进相关文献的相应结果[13-15],更可得出一大批级数部分和不等式。 [1] 陈纪修.数学分析[M].2版.北京:高等教育出版社,2009. [2] 胡克.解析不等式的若干问题[M].湖北:武汉大学出版社,2007. [3] 隆建军.Shapiro不等式的指数推广[J].佳木斯大学学报:自然科学版,2012,30(1):121-123,131. [4] 隆建军.关于推广的Shapiro不等式及其应[J].宜宾学院学报:自然科学版,2013,13(6):8-11. [5] 曾庆黎.Minkowshi不等式的一个证明[J].北京联合大学学报:综合版,1994(3):70-73. [6] 魏巍,乔建斌.Minkowshi不等式两种形式的推广[J].中北大学学报:自然科学版,2013(2):109-111. [7] 阳凌云.离散型H.Minkowshi不等式的拓广[J].株洲工学院学报,2005(1):35-36. [8] 吴树宠.Holder不等式和Minkowshi不等式的推广[J].数学学报,2006(6):1267-1274. [9] 罗静.用Eξ2≥(Eξ)2证明一类级数部分和不等式[J].四川理工学院学报:自然科学版,2012,25(6):65-68. [10] 吴振奎.数学的创造[M].哈尔滨:哈尔滨工业大学出版社,2011. [11] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2014. [12] 匡继昌.Hilbert不等式研究的新进展[J].北京联合大学学报:自然科学版,2010(1):51-53. [13] 沈艳.Shapiro不等式的改进[J].湖南科技学院学报,2006(5):28-30. [14] 季明银.一类不等式的推广[J].北京:数学通报,2008(1):60-61. [15] 文开庭.Shapiro不等式及其变形的新推广与应用[J].贵州教育学院学报:自然科学版,2006(2):4-6. A Kind of Series Part and Inequality and Its Application LUOJing (School of Science, Sichuan University of Science & Engineering, Zigong 643000, China) Series part and inequality is the foundation of inequality research and the development of modern mathematics. Based on the study of classical inequalities, series part and inequality with multiple parameters and simple structure form is established. In the application of some basic inequalities, the inequality is strictly proved by elementary transformation. Based on the analysis of the structure characteristic of the inequality and the given specific parameters value, a series of important corollaries are presented. Through several notable examples, the test theorem and its corollary are universal in constructing or proving a large number of series and inequalities. At the same time, the results not only include a large number of well-known inequalities, but also are the promotion, improvement and enhancement of these inequalities and the recent literature. basic inequality; series part and inequality; generalization 2016-03-24 罗 静(1980-),女,四川自贡人,助教,主要从事数学分析与复变函数理论方面的研究,(E-mail) 379040763@qq.com 1673-1549(2016)04-0081-07 10.11863/j.suse.2016.04.18 O178 A
2主要结果及证明

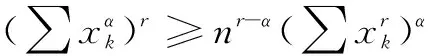
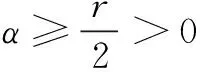
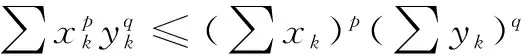

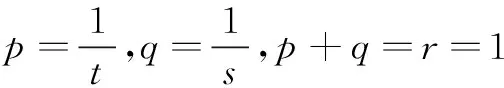

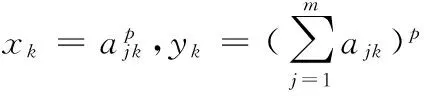
3实例




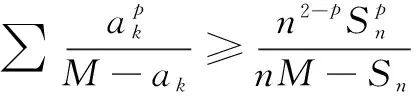
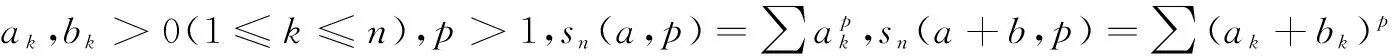
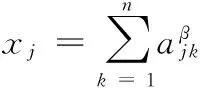
4结束语

