高阶系统时滞反馈的部分极点配置问题

解婷婷， 郎英

(成都理工大学管理科学学院， 成都610059)



高阶系统时滞反馈的部分极点配置问题

解婷婷， 郎英

(成都理工大学管理科学学院， 成都610059)

高阶系统部分极点配置问题是通过计算反馈矩阵将系统测得的不期望的特征值替换成想要的特征值，同时能够保持其余特征结构不变。这个问题常出现在动力结构主动控制系统中。在实际中，传感器测量、处理器计算等都需要一定的时间，导致控制力出现时间滞后现象，即高阶系统时滞反馈的部分极点配置问题。一般方法解决这个问题的过程会使用响应矩阵或解希尔维斯特方程，从而比较复杂，计算量大。文章提出一种明确的单输入算法解决这个问题，方法的优点是简单有效、易于实现，且在过程中没有使用响应矩阵等构成复杂的运算。实例验证了该方法的有效性和实用性。

反问题；部分极点配置；高阶系统

引言

考虑带时滞高阶系统[1]：

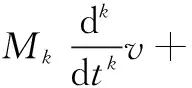
M0v=f(t-τ)

(1)

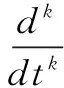
一般地，令f(t-τ)=Bu(t-τ)，其中B∈Rn×m是满秩控制矩阵，u(t-τ)是反馈控制变量。即

(2)

其中，F0,F1,…,Fk-1∈Rn×m是状态反馈控制矩阵，从而得到闭环时滞系统：

(3)

利用变量分离v(t)=xeλt,x∈C,λ∈Cn，代入(3)式得到闭环时滞特征值问题

Pτ(λ)x=0

(4)

其中，

这类问题如：航空航天和汽车工业结构力学与声学系统的振动分析，电路仿真，流体力学和有限元模型更新[1-4]等。

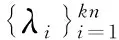
对于高阶系统问题，文献[8]通过单输入状态反馈控制，应用正交方法配置期望的特征值并且保持其余的特征值不变。文献[13]解决部分特征值配置问题基本上解决了一个非常低的顺序的线性系统的极点配置。Wang[14]建立了新的正交关系，考虑了状态反馈的高阶系统的部分极点配置问题。Tehrani[15]提出利用响应矩阵求解部分极点配置问题的一种混合方法。一般方法如文献[9-10,12]都使用了响应矩阵或希尔维斯特方程，此方法需要闭环响应矩阵，使得矩阵变成敏感的测量噪声，而变得不确定。本文提出的方法没有使用响应矩阵或希尔维斯特方程。

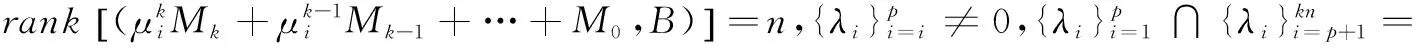
Λ=diag(λ1,λ2,…,λkn)，其对角元素是开环系统的特征值。

Λ1=diag(λ1,λ2,…,λp)，其对角元素是不期望的特征值。

Λ2=diag(λp+1,λp+2,…,λkn)，其对角元素是其余保持不变的特征值。

X=[x1,x2,…,xkn]，其每一列是开环系统中每个特征值相应的特征向量。

X1=[x1,x2,…,xp]，X2=[xp+1,xp+2,…,xkn]。

1问题1的解

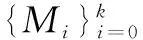
(5)

则对任意的β，有

(6)

(6)式说明矩阵束P(λ)=λkMk+λk-1Mk-1+…+M0，其余的kn-p个特征对(Λ2,X2)也就是修正后的矩阵束Pτ(λ)的特征对。

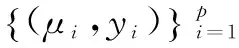
Σ1=diag(μ1,μ2,…,μp)，Y1=[y1,y2,…,yp]

(7)

针对问题1的解，需要选择任意β，使

(8)

(9)

其中，

令

(10)

作γ=(1,1，…，1)，则

Hβ=γT=eτΣ1(1,1,…,1)T

(11)

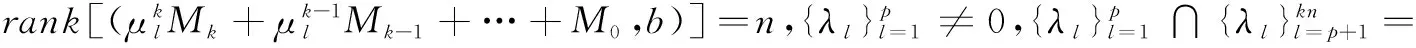
(2)作yl(l=1,2,…,p)满足

(12)

证明根据引理1，定理1中(1)显然成立。

由(9)式和γ=(1,1，…，1)，则有

(13)

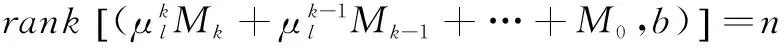
由(10)式，有

(14)

因而

从而有

hlm=

(15)

(16)

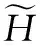
依据定理1，可以得到下面的算法：

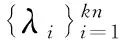
(1)作矩阵Λ1=diag(λ1,λ2,…,λp)andX1=[x1,x2,…,xp];

(2)for i=1,2,…,p do

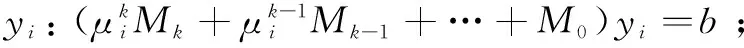
(4)end for

(5)Σ1=diag(μ1,μ2,…,μp)，Y1=[y1,y2,…yp];

(7)求β:Hβ=eτΣ1(1,1,…,1)T;

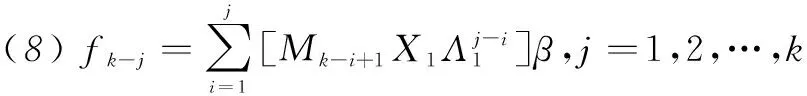
2数字实例

例1考虑三阶系统

开环系统的4个特征值：λ1,2=±i，λ3,4=-1±2i，时滞τ=0.1，控制向量b=(1,0)T。为了使系统稳定，将替换前两个共轭特征值λ1,2为μ1,2=-1±i，则Λ1=diag(+-i)，且相应矩阵的特征向量为：

依据算法1，计算得

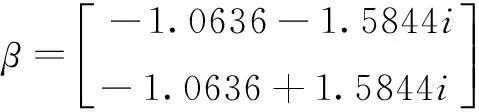
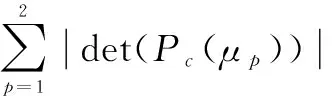
3结束语

本文提出了一个明确的算法解决高阶系统受时滞影响的部分极点配置问题。该方法可以配置期望的特征值，并且保持无溢出特性。且比较容易实现，没有应用响应矩阵或解希尔维斯特方程，具有较强的实用性。

[1] 周树荃,戴华.代数特征值反问题[M].郑州:河南科学技术出版社,1991.

[2] 朱安文,曲广吉.结构动力模型修正技术的发展[J].力学进展,2002,32(3):337-348.

[3] 于德介.用优化方法修正阻尼结构动力学模型[J].振动与冲击,1994,13(2):7-13.

[4] CAI Y,QIAN J.Robust partial pole assignment problem for high order control systems[J].Automatica,2012,48(1):1462-1466.

[5] RAM Y M.Partial pole placement with time delay in structures using the receptance and the system matrices[J].Linear Algebra Appl,2011,434(7):1689-1696.

[6] DATTA B N.eigenstructure assignment and eigenvalue embedding techniques for vibrating systems[J].Mech.Syst.Signal Process,2002,16:263-289.

[7] GUO Z,CAI Y.A modified Schur method for robust pole assignment in state feedback control[J].Automatica,2015,52:334-339.

[8] RAMADAN M.Partial eigenvalue assignment problem of high order control systems using orthogonality relations[J].Comput.Math.Appl,2010,59(6):1918-1928.

[9] 杨杰,耿遵敏,谭雪琴.基于复模态的结构有限元动态模型修正理论[J].振动与冲击,2002,21(1):30-32.

[10] MAO X,DAI H.Minimum norm partial eigenvalue assignment of high order linear system with no spill-over[J].Linear Algebra Appl,2013,438(5):2136-2154.

[11] ZHANG L,WANG X.Partial eigenvalue assignment for high order system by multi-input control[J].Mech.Syst.Signal Process,2014,42:129-136.

[12] WANG X,ZHANG L.Partial eigenvalue assignment of high order systems with time delay[J].Linear Algebra Appl,2013,438:2174-2187.

[13] ZHANG L.Multi-input partial eigenvalue assignment for high order control systems with time delay[J].Mechanical Systems and Signal Processing,2016,72:376-382.

[14] RAM Y M,MOTTERSHEAD J E.Receptance method in active vibration control[J].AIAA J.,2007,45:562-567.

[15] TEHRANI M G,MOTTERSHEAD J E.Robust pole placement in structures by the method of receptances[J].Mech.Syst.Signal Process,2011,25:112-122.

[16] LIU H,YUAN Y X.A multi-step method for Partial quadratic pole assignment with time delay[J].Applied Mathematics and computation,2016,283:29-35.

Partial Pole Assignment Problem for High Order Systems with Time Delay

XIETingting,LANGYing

(College of Management Science, Chengdu University of Technology, Chengdu 610059, China)

The partial pole assignment problem for high order systems with time delay is considered, which the unwanted eigenvalues are moved to desired values and all other eigenpairs remain unchanged by calculation feedback matrix. The problem often appeared in the power structure in the active control system. In practice, these processes such as sensor, processor, calculation and so on take time, which lead to control time lag phenomenon. That was partial quadratic pole assignment problem with time delay. A general method to solve this problem is using the receptance matrix or solve the Sylvester, which is more complex and need large amount of calculation. A clear single input algorithm to solve this problem is presented in this paper. The advantage of this method is simple, effective, easy to implement, and have no complex calculations caused by response matrix. Finally, algorithm implementation and numerical examples show that the proposed method is effective and practical.

inverse problem; partial pole assignment; high order systems

2016-06-01

解婷婷(1990-)，女，陕西渭南人，硕士生，主要从事运筹学与控制论方面的研究，(E-mail)stapf1314@163.com

1673-1549(2016)04-0097-04

10.11863/j.suse.2016.04.21

O231

A