分担值与正规族

吕凤姣， 蒋红敬

(黄河科技学院信息工程学院， 郑州450063)



分担值与正规族

吕凤姣， 蒋红敬

(黄河科技学院信息工程学院， 郑州450063)

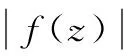
亚纯函数；分担值；正规族

1引言及主要结果

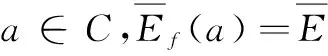
定义2设f(z),g(z)为区域D上的两个亚纯函数，对复数a∈C,若f(z)-a的零点为zn(n=1,2,3,…)，如果zn(n=1,2,3,…)也是g(z)-a的零点(不计重数)，则称单向分担a，记为f(z)=a⟹g(z)=a。

定义3设F为复平面一区域D上的一族亚纯函数，如果从F中任取一函数序列{fn(z)}均可选出一子序列{fnk(z)}在区域D上按球距内闭一致收敛于一亚纯函数或∞，则称F在区域D上正规。

定理1[3]设f(z)是一个非常数亚纯函数，如果f(z)和f′(z)IM分担三个不同的复数a1,a2,a3,则f≡f′。

定理2[4]设F={f(z)}是单位圆盘Δ上的亚纯函数族，a1,a2,a3是三个不同的复数，如果对每个f∈F，f与f′同时分担值a1,a2,a3，则F在Δ上正规。

定理3[5]设F是D上的一亚纯函数族，a和b是两个不同的复数，如果对任一f∈F，f(z)与f′(z)在D内IM分担a,b，则F在D内正规。

定理4[6]设F是单位圆盘Δ上的一亚纯函数族，a是一个非零的有穷复数，如果对任一f∈F，f(z)与f′(z)在Δ内IM分担a，且f(z)的零点是重级的，则F在Δ内正规。

定理5[7]设F是单位圆盘Δ上的一亚纯函数族，a和b是任意两个非零有穷复数，k为正整数。如果对任一f∈F，f(z)的零点重级至少是k+1，且f(z)=a⟺f(k)(z)=b，则F在Δ上正规。

这时，自然地就会考虑定理中的条件能否进一步减弱为单向分担，本文证明了如下定理：

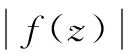
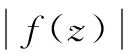
2相关引理

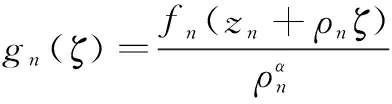
这里g(ζ)为复平面上的一个亚纯函数，其零点(极点)重级均≥k(j)，且g#(ζ)≤g#(0)=1。

注这是Zalcman引理的推广，亦称为Zalcman引理，其中当k=1,j=1,α=0时是Zalcman最早的结果。该形式是文献[12-14]推广而得到的。

这里g(ζ)为复平面上的一个非常数亚纯函数，其零点重级至少为k，且g#(ζ)≤g#(0)=kA+1。特别地，g(ζ)的级至多为2。

引理3[16](Hurwitz定理)设函数序列{fn(z)}在区域D内解析，并且在D内闭一致收敛到一个不恒为零的函数，γ是D内可求长的闭曲线，其内部属于D，且不经过f(z)的零点，则存在正整数N，使得当n≥N时，在γ内部，fn(z)和f(z)的零点个数是相同的。

引理4[17-18]设f(z)为复平面上的有穷级亚纯函数，b为非零复数，k为正整数。若f(z)的零点重级至少为k+1，极点重级至少为2，且f(k)(z)≠b，则f(z)为一常数。

3定理6的证明

又g(ξ)的零点重级至少为k+1，极点重级至少为2，由引理4知：g(ξ)为一常数，这与g(ξ)是非常数亚纯函数矛盾。从而定理6得证。

4结束语

目前，将正规族理论应用到亚纯函数唯一性的研究中，已取得了一些很好的结果。另外，正规族的基础理论在复动力系统的Julia集分形和拟共形映照理论等方面有着广泛的应用。

[1] 杨乐.值分布论及其新研究[M].北京:科学出版社,1982.

[2] 顾永兴,庞学诚,方明亮.正规族理论及其应用[M].北京:科学出版社,2007.

[3] MUES E,STEINMETZ N.Meromorphe funktionen,diemit ihrer ableitung werte teilen[J].Manuscripta Math.,1969,29:195-206.

[4] SCHWICK W.Sharing values and normality[J].Arch Math,1992,59:50-54.

[5] PANG X,LAWRENCE Z.Normality and shared values[J].Arkiv for Matematik,2000,38:171-182.

[6] 章文华.分担值和正规族[J].数学研究与评论,2005,25(2):307-310.

[7] FANG M L,ZALCMAN L.Normal families and shared values of meromorphic functions[J].Annals Polonici Mathematici,2003,80:133-141.

[8] ZHANG G M,PANG X C,ZALCMAN L.Normal families and omitted functions II[J].Bull London Math Soc,2009,41:63-71.

[9] 王雪琴.亚纯函数的分担值与正规族[J].数学物理学报,2014,34A(4):1008-1013.

[10] 李三华,刘忠东,吴高翔.与分担值相关的正规族[J].华东师范大学学报:自然科学版,2013(1):54-60.

[11] ZALCMAN L.A heuristic principle in complex function theory[J].Ame Math Mont,1975(82):813-817.

[12] PANG X.Blochs principle and normal criterion[J].Sci China Ser A,1989(32):782-791.

[13] SCHWICK W.Normality Crietion for families of meromorphic functions[J].Anal Math,1989(52):241-289.

[14] 陈怀惠,顾永兴.Marty定则的改进及应用[J].中国科学A辑,1993,23(2):123-129.

[15] PANG X C,ZALCMAN L.Normality families and shared values[J].Bull London Math Soc,2000,32:325-331.

[16] 方企勤.复变函数教程[M].北京:北京大学出版社,1996.

[17] HAYMAN W K.Picard Value of Meromorphe functions And Their Derivatives[J].Annals of Mathematics,1959,70:9-42.

[18] LI S,GAO Z.Results on a question of Zhangand Yang[J].Acta Math.Sci.Ser.B Engl.Ed.,2012,32(2):717-723.

Shared Values and Normal Families

LVFengjiao,JIANGHongjing

(College of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450063, China)

meromorphic functions; shared values; normal family

2016-04-19

吕凤姣(1983-)，女，河南商丘人，讲师，硕士，主要从事复分析方面的研究，(E-mail)lvfengjiao_2008@163.com

1673-1549(2016)04-0078-03

10.11863/j.suse.2016.04.17

O174.52

A