n个同型部件和k个修理设备的并联可修系统的可靠度探究

梁丽丹

(伊犁师范学院数学与统计学院， 新疆伊宁835000)



n个同型部件和k个修理设备的并联可修系统的可靠度探究

梁丽丹

(伊犁师范学院数学与统计学院， 新疆伊宁835000)

在假定部件的工作寿命服从参数为λ的指数分布，维修时间服从参数为μ的指数分布，部件的状态转换开关时是瞬间完成的，在初始时刻，所有部件都正常，所有随机变量均相互独立，故障部件能够修复如新的条件下，对由n个同型部件和k(k≤n)个修理设备组成的并联可修系统的可靠度进行分析。通过建立该系统的模型，计算出可靠度通式，并对n=2,k=1时的结果进行了验证。

并联可修系统；转移矩阵；可靠度；L变换

引言

并联系统在可修系统中非常重要，其可靠度情况在具体的实际应用中具有重要作用。董兵等[1]研究了具有优先修理权的两个不同部件并联系统的可靠性分析。汪文珑等[2-3]对由两个并联部件构成的可修系统进行了分析。程江等[4]研究了修理设备可以更换的三部件串-并联可修系统的可靠性。汪军芳等[5]研究了两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性。Weili等[6]对两个修理工的情况进行了讨论。可见，目前主要是对二部件或三部件的并联系统进行了相关研究与讨论[7-10]。对于大型系统，系统组成会相对庞大，会有更多的部件构成，在实际应用中多个部件多个修理设备的可靠度在工作和预防维修中均起到指导作用，可以提高经济效益。为此本文研究了n个同型部件和k个修理设备的并联可修系统的可靠度，通过构造模型进行分析计算，得出此n个同型部件和k个修理设备的并联可修系统的可靠性指标，并且验证了当n=2,k=1时，此系统的结论与文献[11]的结论一致。

假定

(1)由n个同型部件和k个修理设备组成的系统，假定所有随机变量是相互独立的，由于有k个修理设备，当有k+1或k+1以上的部件发生故障时，只能修理其中k个，其余故障部件处于待修状态，部件的状态转换开关时完全可靠且转换是瞬间完成的。

(2)所有部件的工作寿命分布为1-e-λt,t≥0(λ>0)，工作故障部件的修理时间分布为1-e-μt,t≥0(μ>0)。

(3)在初始时刻0，所有部件都正常。

1模型分析

系统共有n+1个不同的状态，令N(t)=j,若t时刻系统中有j个故障部件(包括正在修理的部件)，j=0,1,...,n。根据并联系统[12]的定义，状态n是系统的故障状态，因此，状态空间E={0,1,...,n}，工作状态W={0,1,...,n-1}，故障状态F={n},{N(t),t≥0}是状态空间为E的时齐马尔可夫过程，Δt时间内不同状态之间的转移概率为：

Pjj+1(Δt)=(n-j)λΔt+0(Δt);j=0,...,n-1

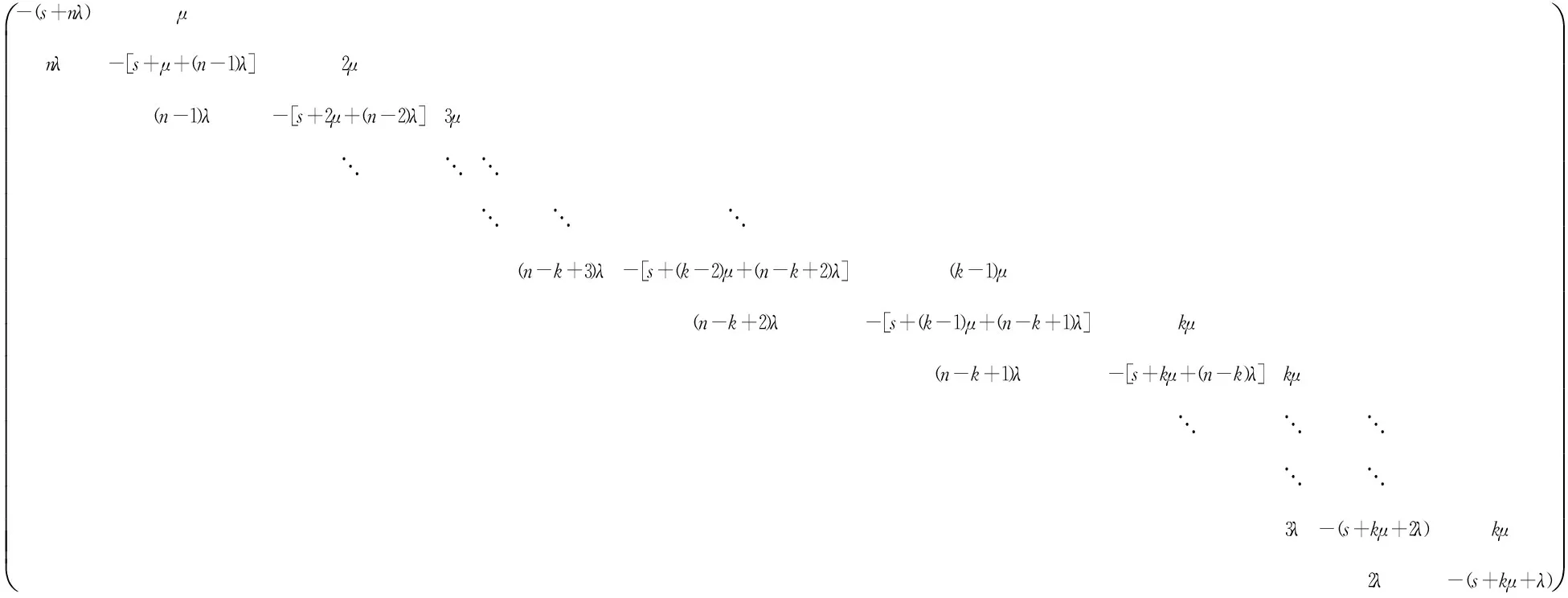
由连续时间Markov链的性质，不难写出其转移率矩阵[13]

D=(qij)=

其中，

2系统可靠度

为求系统的可靠度，解方程

其中A矩阵为D矩阵去掉最后一行和最后一列的矩阵，对方程作L变换[14]得

写成矩阵的形式为：

其中

设B-1=C

-(C11+ C21+ ... + Cn1)

运用求矩阵逆[15-16]的方法可得

…

则

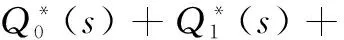
由于p1p2...pn是关于s的n次方程，设si(i=1,2,...,n)是其根，作L的逆变换得

R(t)=Q0(t)+...+Qn-1(t)=

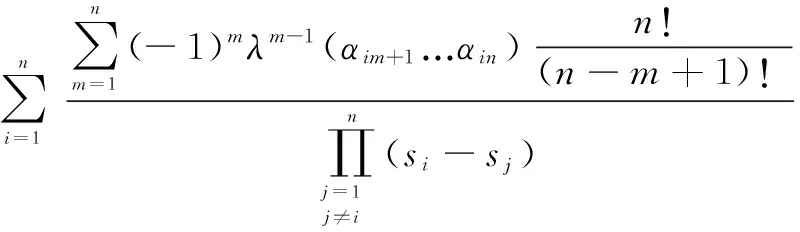
p1=-(s+nλ)

⋮

pk-1=-[s+(k-2)μ+(n-k+2)λ]-

pk=-[s+(k-1)μ+(n-k+1)λ]-

⋮

可得到

pm=-[s+(m-1)μ+(n+1-m)λ]-

1≤m≤k+1pm=-[s+kμ+(n+1-m)λ]-

另有α的值

⋱

αk-1=-[s+(k-2)μ+(n-k+2)λ]-

αk=-[s+(k-1)μ+(n-k+1)λ]-

⋱

αn=-(s+kμ+λ)

可得

αn=-(s+λ+kμ),(k

k+1`≤u≤n-1

αu=-[s+(u-1)μ+(n+1-u)λ]-

u=k,k-1,…1,αiu=-[si+kμ+(n+1-u)λ]-

αiu=-[si+(u-1)μ+(n+1-u)λ]-

u=k,k-1,…1αin=-(si+λ+kμ)

3特别的情况

当k=1时，为n个同型部件一个修理设备的情形

(1)n=2,k=1时，用通式

其中

p1=-(s+2λ)

α2=-(s+λ+μ)

所以

p1p2=s2+s(3λ+μ)+2λ2

设s1,s2为s2+s(3λ+μ)+2λ2=0的两根，且小于0。

与文献中结果一致。

(2)容易得出n=3,k=1的可靠度，用同样的方法可得

其中

p1=-(s+3λ)

α3=-(s+λ+μ)

所以

p1p2p3是关于s的三次方程，设s1,s2,s3为其根，由matlab计算的每一s都小于0。

R(t)=

4结束语

通式应用广泛，当k=1时转换为一个修理设备的情形，k≠1时，为k个修理设备的情形，从而多元件并联系统的可靠度可方便求出。

[1] 董兵,唐应辉.具有优先修理权的两个不同部件并联系统的可靠性分析[J].黑龙江大学学报:自然科学学报,2007,24(2):249-252.

[2] 汪文珑,张斌.两个并联部件的可修系统的谱分析及其应用[J].绍兴文理学院学报:自然科学版,2013,33(1):1-8.

[3] 张欣,何云,李琳.两不同型部件并联可修系统主算子的性质[J].数学的实践与认识,2013,43(8):232-237.

[4] 程江,唐应辉.修理设备可以更换的三部件串-并联可修系统的可靠性[J].西南大学学报:自然科学版,2010,32(1):148-154.

[5] 汪军芳,张民悦.两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性[J].四川理工学院学报:自然科学版,2015,28(1):80-82.

[6] WEILI A S,YIQIANG Q Z.Stochastic analysis of a repairable system with three units and two repair facilities[J].Microelectronics Reliability,1998,38(4):585-595.

[7] 王丽英,刘宝友,王永亮.随机选择修理工的可修系统的可靠性分析[J].石家庄铁道学院学报,2006,19(4):104-106.

[8] 雷小平,蔡静,赵明.基于系统隐藏寿命数据的串联系统可靠性估计[J].贵州大学学报:自然科学版,2006,23(3):245-248.

[9] 成国庆,李玲,唐应辉.不能修复如新的两部件串联系统的可靠性分析[J].数学的实践与认识,2008,38(10):77-83.

[10] 刘学娟,王文彬,彭锐,等.基于延迟时间理论的两部件并联系统检测区间模型[J].数学的实践与认识,2015,45(7):231-239.

[11] 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006.

[12] 程侃.寿命分布类与可靠性数学理论[M].北京:科学出版社,1999.

[13] 牛裕琪,袁中许.可修并-串联系统的状态转移空间分析[J].许昌学院学报,2005,24(5):19-21.

[14] DDER D V.The laplace transform[M].Princeton,New Jersey:Princeton University Press,1941.

[15] 杨胜良.三对角行列式及其应用[J].工科数学,2002,18(2):102-104.

[16] 冉瑞生,黄廷祝.三对角矩阵的逆[J].哈尔滨工业大学学报,2006,38(5):815-817.

Study on Reliability of Paralleled Redundant Repairable System withnIdentity Units andkRepair Facilities

LIANGLidan

(Department of Mathematics and Statistic, Yili Normal University, Yining 835000, China)

Under assumption that the working life of the components subject to the exponential distribution with parameter λ and maintenance time obey the exponential distribution with parametersμ, the switch is instantaneous, all the parts is normal at the initial time and all random variables are independent of each other. Under the condition of the fault parts can be repaired as new, the reliability of the parallel repairable system which consisted of n identity units and k repair facilities is analyzed. By establishing the model of the system, reliability formula is computed. The reliability is verified for the conclusion of n=2, k=1.

parallel repairable system; transfer matrix; reliability; L conversion

2016-04-16

梁丽丹(1985-)，女，河南洛阳人，助教，硕士，主要从事可靠性理论分析方面的研究，(E-mail)lianglidan123@126.com

1673-1549(2016)04-0088-06

10.11863/j.suse.2016.04.19

O213.2

A