二值图像逻辑与运算CNN模板的稳定性设计
李硕, 魏小亭, 李国东,b
(新疆财经大学a.应用数学学院;b.新疆社会经济统计研究中心, 乌鲁木齐830012)
二值图像逻辑与运算CNN模板的稳定性设计
李硕a, 魏小亭a, 李国东a,b
(新疆财经大学a.应用数学学院;b.新疆社会经济统计研究中心, 乌鲁木齐830012)
结合细胞神经网络(Cellular Neural Networks)理论,提出了一类能快速实现二值图像逻辑与运算的模板。对模板稳定性的数学分析表明,只要模板参数符合文中定理的要求,CNN就能够对两幅二值图像进行与运算。实验仿真证明了LOGAND CNN在实际应用中的有效性及稳定性设计定理的正确性。
二值图像;细胞神经网络;逻辑与运算;稳定性设计
引言
细胞神经网络(CNN,cellular neural network)是由蔡少棠和杨林[1-2]在1988年提出的。目前,大型集成电路已经可以实现细胞神经网络的功能,而且它也在许多重要领域得到应用[3-9]。CNN的模板参数决定了它的功能,参数的多样性使得CNN的图像处理功能十分强大。因此研究模板参数在什么范围内能使CNN实现特定功能,并使CNN具备稳定性[10-12]有很大的研究意义。Chua L O提出了二值图像逻辑与(LOGAND)CNN的模板[5]。丁蕾研究了一种对二值图像进行逻辑运算的改进算法[13]。张群等[14]研究了一类能对灰度图像进行逻辑或的CNN。有研究发现,CNN处理器的图像处理速度理论上要比数字处理器快1000倍[5],表明了此算法的优越性。本文对Chua L O给出的LOGAND CNN模板参数进行了扩展,提出了一个符合二值图像逻辑与运算的定理。
标准的M×N的CNN是由细胞Ci,j构成,其结构基本形式如图1所示。每个细胞Ci,j的状态方程[5]为:

∑B(i,j;k,l)ukl+z
(1)

图1二阶CNN的结构图
输出变量yi,j是由下述分段函数定义的:
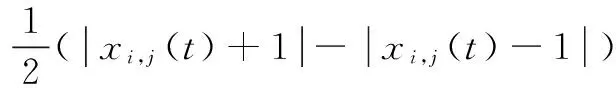
1≤i≤M;1≤j≤N
(2)
其中,xi,j、yi,j、ui,j和z分别表示为状态变量、输出变量、输入变量和阈值;A(i,j;k,l)和B(i,j;k,l)为两个矩阵,A为反馈模板,B为控制模板。状态方程的动力学性质就由模板A、B和偏移z来决定。标准的CNN的输出函数如图2所示。

图2标准CNN输出函数
1二值图像与运算CNN

(3)
为了确保像素点是一一对应的,要求两幅进行逻辑与运算的二值图像尺寸必须相同。任何一个像素点对应的输入和初值只能为1或-1,只有当对应像素点的输入和初值全为1(黑像素)时,输出才为1;否则,输出为-1,即白像素。其模板由式(4)给出

(4)
1.1LOGAND CNN的整体任务
LOGAND CNN的整体任务如下:
(1) 给定两幅静态二值图像P1和P2。
(2) 输入图像:U=P1。
(3) 初始状态图像:X(0)=P2。
(4) 边界条件:周期(toroidal)边界条件。

1.2LOGAND CNN的局部规则
由LOGAND CNN的整体任务可以看出,它的输出结果仅与它的输入和初始的状态有关系,输入和初始状态共有4种组合形式:(1,1)、(1,-1)、(-1,1)、(-1,-1)。按照这4种情况,可以将整体任务分成4个局部规则:
(1) (ui,j,xi,j(0))=(1,1)⟹yi,j(∞)=1;
(2) (ui,j,xi,j(0))=(1,-1)⟹yi,j(∞)=-1;
(3) (ui,j,xi,j(0))=(-1,1)⟹yi,j(∞)=-1;
(4) (ui,j,xi,j(0))=(-1,-1)⟹yi,j(∞)=-1;
所以,对待处理的二值图像P1和P2,LOGAND CNN的4个局部规则可以归纳为表 1 的形式。

表1LOGAND CNN模拟二值图像逻辑与运算的局部规则
1.3LOGAND CNN模板稳定性定理及证明
LOGAND CNN的逻辑与运算功能是用线性非耦合模板式(4)来实现的,它是LOGAND CNN的一种特殊形式。这里仿照上述模板,采用下文的一般线性非耦合模板来实现LOGAND CNN的功能。

(5)
其中,a、b、z为实数,且a>1,b>0。
则LOGAND CNN的状态方程为:

-xi,j+ayi,j+bui,j+z
(6)
定理1设二值数字图像逻辑与运算CNN的模板为式(5)所示形式,那么当式(7)表示的不等式组成立时,CNN能够实现二值图像逻辑与运算的功能。

(7)
证明将LOGAND CNN的状态方程式(6)写为
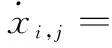
-xi,j+ayi,j+wi,j,
i=1,2,…M; j=1,2,…N
(8)
其中,wi,j=bui,j+z。


图3单个LOGAND CNN的动力学曲线
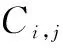
wi,j=bu+z=-2b+z (9) (2) ui,j(0)=-1,且xi,j(0)=1⟹yi,j(∞)=-1。可得Ci,j的动力学曲线,位于图3中的wi,j=0曲线下方(即bu+z<0)。得到 wi,j=bu+z=z<0 (10) (3) ui,j(0)=1,且xi,j(0)=1⟹yi,j(∞)=1。可得Ci,j的动力学曲线,位于图3中的wi,j=1-a曲线上方(即bu+z>1-a)。得到 wi,j=bu+z=2b+z>1-a (11) z<0 (12) 由式(9)~式(12)与a>1,b>0可得(7)式。 定理1证明完毕。表明只要CNN的模板参数满足定理1中式(7)的要求,就能够完成对数字二值图像进行逻辑与运算的任务。 {a=2,b=1,z=-1} {a=10,b=2,z=-2} {a=100,b=20,z=-10} 三组参数模拟的结果如图4(c)所示,可以看出实验仿真的效果很好。 为了避免实验结果的偶然性,选取不同的图像P3(图5(a))和P4(图5(b))进行实验仿真,同样选取三组不同的(满足定理1)的模板参数: {a=20,b=10,z=-3} {a=200,b=100,z=-20} {a=300,b=200,z=-30} 结果如图5(c)所示。 综上,当选择的模板参数满足定理1的要求时,LOGAND CNN便能对两幅静态二值数字图像完成逻辑与运算,且效果比较理想,确认了定理1的可行性与正确性。 图4LOGAND CNN模拟二值图像P1和P2的与运算 图5LOGAND CNN模拟二值图像P3和P4的逻辑与运算 通过对Chua L O给出的LOGAND CNN模板参数进行扩展,给出了一个适用于二值图像逻辑与运算的定理,并对该定理进行了严格的数学证明。只要LOGAND CNN的模板参数满足定理的要求,就可以完成对两幅二值图像的逻辑与运算。实验结果证明了LOGAND CNN的有效性、稳定性以及设计定理的正确性。该LOGAND CNN具有所有CNN的高速运算功能,使得此算法在实际图像处理过程中具有很大的优越性。 [1] CHUA L O,YANG L.Cellular neural networks:theory[J].IEEE Transactions on Circuits & Systems,1988,35(10):1257-1272. [2] CHUA L O,YANG L.Cellular neural networks:applications[J].IEEE Transactions on Circuits & Systems,1988,35(10):1273-1290. [3] 李国东,王雪,赵国敏.基于五阶CNN的图像边检测算法研究[J].安徽大学学报:自然科学版,2015,39(3):15-21. [4] 张爱华,雷小亚,陈晓雷,等.基于细胞神经网络的快速手语视频分割方法[J].计算机应用,2013,33(2):503-506. [5] CHUA L O.CNN:a visions of complexity[J].International Journal of Bifurcation & Chaos,1997,7(10):2219-2425. [6] ZANELA A,TARAGLIO S.Sensing the third dimension in stereo vision systems:a cellular neural networks approach[J].Engineering Applications of Artificial Intelligence,1998,11(2):203-213. [7] HADAD K,PIROOZMAND A.Application of cellular neural network (CNN) method to the nuclear reactor dynamics equations[J].Annals of Nuclear Energy,2007,34(5):406-416. [8] 涂小辉,许杰,张莲.五阶离散CNN超混沌数字化研究[J].现代电子技术,2011,34(3):101-103. [9] 任晓霞,廖晓峰,熊永红.基于细胞神经网络超混沌特性的图像加密新算法[J].计算机应用,2011,31(6):1528-1530. [10] MIN L Q.Robustness designs of a kind of uncoupled CNNs with applications[C]//Proceeding of 2005 9th International Workshop on Cellular Neural Networks and Their Applications,Hsinchu,Taiwan,May 28-30,2005:98-101. [11] LIU J Z,MIN L Q.Robust design for templates of directional extraction cellular neural network with applications[J].International Journal of Pattern Recognition and Artificial Intelligence,2009,23(1):63-66. [12] LIU J Z, MIN L Q.Robust design of bipolar wave cellular neural network with applications[J].International Journal of Modelling Identification & Control,2010,11(1-2):99-106. [13] 丁蕾.快速图像逻辑运算VC++算法[J].广西师范学院学报:自然科学版,2011,28(3):88-92. [14] 张群,闵乐泉.灰度图像逻辑或运算CNN模板的顽健性设计[J].通信学报,2014,35(5):88-94. The Stability Design of Binary Image Logic and CNN Template LIShuoa,WEIXiaotinga,LIGuodonga,b (a.School of Applied Mathematics; b.Research Center of Xinjiang Social and Economic Statistics, Xinjiang University of Finance & Economics, Urumqi 830012, China) A kind of binary image logic and CNN was proposed by combining with CNN theory. A theorem was established to design the stability template parameters of LOGAND CNN, and a rigorous mathematical proof was given. As long as the template parameters conform to the requirements of the theorem, CNN can conduct and operations for two binary image. The simulation results illustrate the effectiveness and the correctness of the LOGAND CNN in practical application. binary image; cellular neural networks; logical or operation; stability design 2016-05-31 国家自然科学基金项目(11461063);国家社科基金项目(14BTJ021);国家教育部人文社会科学基金项目(13YJAZH040);新疆维吾尔自治区普通高等学校人文社会科学重点研究基地基金项目(050315B03) 李 硕(1988-),男,河北保定人,硕士生,主要从事数据分析与图像处理方面的研究,(E-mail)15026066340a@sina.com; 李国东(1972-),男,黑龙江鹤岗人,教授,博士,主要从事数据分析与图像处理方面的研究,(E-mail)lgdzhy@126.com 1673-1549(2016)04-0044-05 10.11863/j.suse.2016.04.10 TP183 A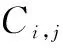
2实验结果
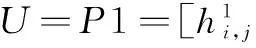
3结束语



