基于协整理论的研究生教育与科技的协调发展分析

张连华 丁咏梅 余艳 傅江浩

(武汉科技大学保卫处,湖北武汉430081)

基于协整理论的研究生教育与科技的协调发展分析

张连华 丁咏梅 余艳 傅江浩

(武汉科技大学保卫处,湖北武汉430081)

探讨我国研究生教育和科技发展的长期稳定关系,构建二者的测度模型,结果表明,我国研究生教育与科技互为Granger因果关系,建立协整关系模型,采用统计指标优化模型。

研究生教育;科技;协整理论;协调发展;Granger因果关系

作为国家最高层次的教育,研究生教育担负着培养高层次创新人才和发展现代科技的双重任务,也是提升国际竞争力的重要支柱。2014年1月发布的《教育部2014年工作要点》中明确指出:“深入推进研究生教育综合改革,不断完善学术和专业学位研究生培养模式,统筹构建研究生教育质量保障体系,继续推进科教结合培养高层次人才”是“促进高校加强质量保障体系建设”的重要举措,因此,如何实现科教结合培养高层次人才,研究生教育和科技如何实现协调发展具有重要的研究意义。

协调是一种状态,这种状态可能存在着不同形式,但应当具有以下可供辨识的特征[1]:第一,系统内各因素的发展状态应当存在且自发形成长期稳定关系;第二,因素之间会相互作用,双向影响。具体到研究生教育与科技的协调发展关系,其内涵也应包括两个方面:一是研究生教育系统中,研究生教育与科技的发展为长期、稳定均衡的关系;若系统内某一因素的出现变化,系统会自动进行调整,以使系统保持稳定;二是系统内研究生教育和科技发展之间应出现相互促进、互为因果的协调关系,研究生教育可促进科技的发展和创新,反过来科技可促进研究生教育的改革和提升。

一、教育与科技协调发展的测度模型

关于研究生教育与科技协调发展的研究是学者们一直在探索的课题。研究方法从基本的观察描述到数理方法论、从定性到定量转化,建立了各种各样的计量模型[2～6],这些方法为协调发展的测度奠定了良好基础。从社会实际中可知,教育,特别是研究生教育与科技的发展应该是双向影响关系,一方面研究生教育是科技创新和发展的培养基地,为科技的发展奠定坚实的理论基础;另一方面,科技的发展激励研究生教育的发展和更新,激励高等教育水平的提升。但不少研究中,结论是“研究生教育与经济、科技形成了相互促进、相互作用的关系,但仅限于经济和科技之间。此外,研究生教育对科技、经济对研究生教育产生单向的显著影响[1]。”这样的研究结论和数据的选择、系统的误差有一定的关系。为了厘清研究生教育与科技的协调发展过程,本研究拟基于协整理论来建构并测度二者的双向协调发展关系的数理模型。

自1987年Engle和Granger在论文《协整与误差修正:描述、估计与检验》中正式提出协整概念以来,协整理论在经济、金融、工业生产等领域得到了快速的发展和应用。系统论指出,同一系统中的某些变量之间确实存在着长期均衡关系,这种均衡关系意味着系统不存在破坏均衡的内在机制。如果变量在某个阶段(或时期)受到干扰后偏离其长期均衡点,则均衡机制将会在下一期进行调整以使其重新回到均衡状态。这种长期稳定的均衡关系称为协整关系。协整理论的提出为在两个或多个非平稳变量间寻找均衡关系以及存在协整关系的变量建立长、短期均衡模型奠定了理论基础。

应用协整理论来测量研究生教育与科技协调发展关系具有以下独特优势:第一,协整理论中协整方程的建立和估计可探测出研究生教育与科技之间是否存在着长期稳定的发展关系;第二,协整方程可对研究生教育与科技数据短期波动状态进行描绘,并进一步考察二者之间是否存在失衡,如果出现偏误,则将短期变动与长期均衡结合,分析短期对长期的调整作用;第三,协整理论中的格兰杰因果关系检验可考察研究生教育与科技在数据层面所呈现的动态因果关系,实现科教系统内指标间的量化测度。[2～8]

假设研究生教育水平和科技因子的长期“均衡关系”由下式描述:

式中,Yt为科技因子;Xt为研究生教育水平;α0为固定效应;α1为研究生教育水平变动一个单位时,对科技因子的影响程度;μt为第t时段的非均衡误差,也被称之为随机扰动项。

式(1)反应了研究生教育水平X和科技水平Y随着时间变化而变化的特征:在第t时段,当研究生教育水平为Xt时,科技水平为α0+α1Xt,该均衡关系意味着给定X的一个值,Y相应的均衡值为μt= Yt-α0-α1Xt;也即表示,设当前的科技固定水平为α0,当研究生教育水平在为X时,科技水平就围绕α0+α1X上下波动,波动幅度为μ。

在实际研究中,许多变量是非平稳的,但若他们是同阶单整序列,则他们的线性组合也可能是平稳的。比如,若上式中X,Y都是I(1)序列,且上式表述的长期均衡关系成立的话,则意味着μt=Yt-α0-α1Xt是I(0)的,此时就称变量X和Y是协整的。这种协整表示,在第t时间段,研究生教育水平Xt科技水平Yt的发展是同步的,若研究生教育水平提高一个单位,科技水平按照线性均衡增长,会提高α1个单位,协变量的延期发展对当期变量有着一定的影响作用。

在进行协整分析前,需要对序列做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,则需要对数据序列进行初始化处理,比如标准化后进行差分或者取对数变换。若序列进行到第i次差分时平稳,则该序列就为i阶单整序列。若所有检验序列均服从同阶单整,可做协整检验,判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。同时,如果序列平稳,则可进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。协整检验的流程如下:序列平稳性检验、Granger因果关系检验、残差序列的单位根检验、设立并估计协整模型、诊断检验并解释结果

二、实证分析

当前,我国的研究生教育呈现飞速发展的态势,学术性和专业型研究生教育同步发展,既要满足科技发展的需要,也要满足企业、社会等用人单位的需要。为了进一步衡量研究生教育和科技的关系,笔者将在校研究生人数作为研究生教育的衡量指标, R＆amp;D(研究开发)经费内部支出作为科技的衡量指标,截取1995年至2012年的样本数据进行分析, (样本来源我国高校研究生录取总人数)。在校研究生人数均值为73.6万人,J-B统计量为1.39,相伴概率为0.47;相应地,R＆amp;D经费内部支出的J-B统计量结果为3.90,相伴概率为0.14。从J-B统计量及其相伴概率可知,在5％的显著性水平下,样本来自渐进正态的总体,取样合理。

事实上,我国研究生教育与科技发展都具有明显的上升趋势,显然呈现出非平稳状态。二者的相关系数为0.886,可见具有高度的线性相关性。为进一步夯实二者的相关关系,对数据进行了如下预处理:首先对两列数据进行标准化,之后进行一阶差分,再对差分结果进行ADF平稳性检验。结果显示,两序列都为一阶单整,由此也得出,研究生教育与可以发展之间具有长期均衡关系。基于以上预处理,对两单整序列做Granger因果检验,结果如表1。

表1 Granger因果关系检验结果

由相伴概率可知,在5％的显著性水平下,二者互为格兰杰因果关系,也即科技的发展受到其自身和研究生教育的影响,反之亦然。于是建立协整方程来考察二者的长期稳定关系。具体模型如下:

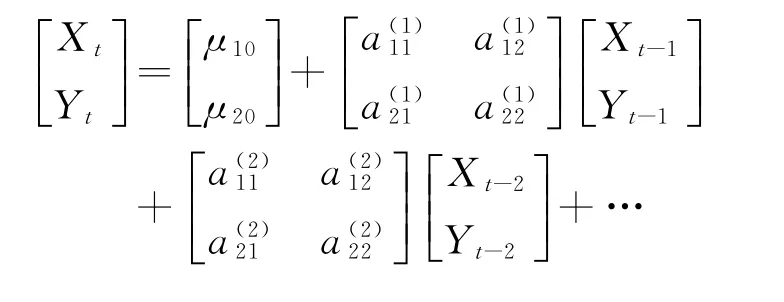
式中,μ10,μ20分别为科技因子Yt、研究生教育水平Xt的随机波动水平;a(1)11,a(1)12为第t-1期的研究生教育水平、科技因子对第t期的研究生教育水平的影响程度;a(1)21,a(1)22为前第t-1期的研究生教育水平、科技因子对第t期的科技水平的影响程度,以此类推;P为研究生教育水平和科技的双向影响的持久期数。

式(2)表明,在时间序列情形下,两个经济变量X、Y之间的存在格兰杰因果关系表示,在包含了变量X、Y的过去信息的条件下,对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果,即变量X有助于解释变量Y的将来变化,则认为变量X是引致变量Y的格兰杰原因。

为了确定合适的模型形式,结合样本数据,对二者相关关系分别刻画出可能的估计方程,详细结果见表2。同时给出评价模型优劣的统计指标,即模型拟合优度R2,线性关系检验F统计量,序列相关性检验D.W.统计量,以及AIC、SC信息准则。结合协整检验的特征值和迹统计量,我们将二者的协整关系判定为模型5和模型9的形式,这两个模型的拟合优度都达到了0.99,表明模型中的自变量对因变量的解释程度非常高,并且D.W.统计量显示,变量间已经没有相关关系,刻画出模型中的自变量对因变量的信息估计是充分的。对比AIC和SC信息准则的估计结果,估计模型5和9也相对较优。

表2 研究生教育和科技的各类拟合模型和优化指标

表2中的各个指标,其含义分别为:ln(Yt)为科技因子Yt取自然对数后的序列,AR(1)为一阶自相关,R2为模型的拟合优度,刻画出每个模型中自变量对因变量的解释程度,越接近于1,表示模型拟合程度越高;F统计量刻画每个模型的具体形式(比如线性的,或者非线性的)是否合理可行,这个指标越大越好;D.W.统计量刻画变量序列的相关性,接近于2表示序列不相关,接近于0表示序列正相关,接近于4表示序列负相关;AIC和SC是评价模型利用信息程度的信息准则,这两个指标同向变化,越小越好。表2中拟合出的10个模型,对照各个统计量的含义,对比各个指标的得分,便可依次推断估计模型对数据的解释程度。例如估计模型1表明,第t时段,科技水平Yt对教育水平Xt的影响为0.18,该模型的拟合优度为0.75,表明当前的科技水平只对教育水平有75％的解释力度,F统计量相对不高,为32.60,D.W.统计量为0.12,表示残差序列存在正向的自相关现象,也即说明,该模型的中的自变量对因变量的解释不够充分,除了当前的Yt外,还有其他因素影响着教育水平Xt,需要对该模型进行改进。

对于估计模型5和9的各个统计指标,由前面分析可知,研究生教育和科技发展之间存在正向相关关系。估计模型5和9的D.W.统计量结果分别为1.92和2.14,也表明估计方程对变量的解释力度是充分的,模型残差之间已经没有相关关系。估计模型9刻画了研究生教育对科技的影响存在着滞后效应,当前教育在4年后对科技的影响程度为e0.08;同时,过去科技的发展对当前的教育进步有激励作用,根据估计模型5,科技向前发展一步,对当前研究生的教育就带来一定的刺激作用,影响水平为8％。

三、结论

笔者基于协整理论测度研究生教育与科技协调发展关系的数理模型,对1995年至2012年我国研究生教育与科技协调发展态势进行了现实考察。实证表明,我国研究生教育与科技之间基本形成了协调发展的态势,并且二者互为Granger因果关系,这种关系并非是一种物理上或者结构上的定义,而是一种预测关系,有助于把握研究生的规模和科技发展态势。协整模型进一步量化了二者的相互关联程度,有助于实现科教发展的协同。

[1]袁本涛,王传毅,冯柳青.基于协整理论的我国研究生教育与经济、科技协调发展研究[J].教育研究,2013(9).

[2]李娟.以职业资格认证为导向,构建专业学位研究生教育外部质量评价体系[N].中国教育报,2014-01-06(2).

[3]王茜,古继宝,吴剑琳.基于内容分析法的研究生导师指导职能研究[J].中国高教研究,2013(9).

[4]王向红,胡宏伟,等.基于协同理论的研究生创新培养体系[J].教育教学论坛,2013(11).

[5]张小波.基于综合评价的研究生教育质量效率指数研究[J].中国高教研究,2013(9).

[6]曲虹,高伟涛.数据包络分析方法在研究生教育投入产出效率评价中的应用[J].北京理工大学学报(社会科学版),2009(12).

[7]车如山,赵静.对我国专业硕士学位研究生教育研究之反思[J].职业技术教育,2013(16).

[8]何植民,曾红权.研究生教育质量的价值取向[J].社会科学家, 2013(9).

责任编辑 胡号寰 E-mail:huhaohuan2@126.com

G643

A

1673-1395(2016)10-0073-03

2016-06-21

湖北省研究生思想政治教育规划课题(2014ZX17);湖北省省级教学研究项目(2014221)

张连华(1979-),男,湖北公安人,讲师,硕士,主要从事思想政治教育研究。