工字轮收线机排线换向控制建模及仿真分析

王培斌 梁久祯 吴 秦 仇 杰

(江南大学物联网工程学院，江苏 无锡 214122)



工字轮收线机排线换向控制建模及仿真分析

王培斌 梁久祯 吴 秦 仇 杰

(江南大学物联网工程学院，江苏 无锡 214122)

针对工字轮在收线过程中存在的排线换向控制问题，给出了排线换向控制的物理模型，建立了排线换向过程的动力学模型。对该数学模型进行了常规PID控制算法的验证性仿真分析，对基于模糊PID控制算法与基于径向基函数(RBF)神经网络PID控制算法在该模型上的应用进行了对比分析。结果表明，所建模型能够正确模拟收线机排线换向过程，基于模糊PID控制算法可以更有效地改善收线机排线换向效果，仿真数据可以为收线机排线换向控制系统的设计与优化提供参考依据。

收线机 动力学模型 RBF神经网络 模糊PID算法 换向控制 数学建模 参数整定 仿真

0 引言

收线机是连续挤压、拉丝行业的重要组成部分，被广泛应用于线缆行业。其收线的平整性和密集性将直接影响到线材质量、线盘单盘容量和收线效率。针对线材缠绕的平整性问题，研究人员通过改进绕线机的机械结构[1]、应用更先进的速度控制算法[2-5]，使绕线过程的控制精度达到相对理想的程度。然而，绕线滞后性带来了排线换向延时需求，随之带来了换向点位置误差导致的排线换向控制问题。

针对排线换向控制问题，文献[6]提出了一种动态补偿算法。由于边缘侧出现的凹陷或凸起会引起收线速度的变化，通过检测该变化、计算并调整换向点位置，达到平整收线的效果。文献[7]则提出了一种无模型学习控制算法。该算法针对线盘两侧出现的绕线凸起或凹陷现象，通过检测线盘两侧边缘处前一层的绕线平整度，控制本层绕线换向点的位置，以平衡绕线过程的总体平整度。

然而，上述研究都直接应用于生产过程，没有具体的理论模型，不能为进一步研究提供理论支撑；并且，其控制过程存在参数整定的问题，这对于换向控制本身而言较为困难。因此，本文在仔细分析收线机绕线过程的基础上，建立了排线换向控制仿真模型；针对PID参数整定问题，对比分析了两大智能整定PID参数的控制算法——基于径向基函数(radial basis function,RBF)神经网络PID控制算法和基于模糊PID控制算法，为进一步研究收线机的排线换向控制提供了数据支持及理论支撑。

1 收线机排线换向分析

收线机的种类有很多种，但其工作原理都是一致的。本文以卧式工字轮收线机为例，略去机器本身的控制精度问题，对其排线换向控制系统进行细致分析，并建立相应的数学模型。

鉴于工字轮收线机绕线系统的组成比较复杂，本文在其复杂的组成部件中抽离出收排线系统的主要结构，如图1所示。图1中：①为工字轮；②为排线架；③为导线轮；④为排线架导向光轴；⑤为收卷线材；Dmin和Dmax分别对应工字轮空盘和满盘时的直径值；dm为线材与工字轮的切点和与导线轮的切点在工字轮端面投影之间的直线距离；Dg为导线轮的内槽直径；da为工字轮轴同导线轮轴之间的距离；ω为工字轮的旋转角速度；Dl为线材的线径或线宽；h为工字轮两内边之间的高度，也是排线换向控制的依据。

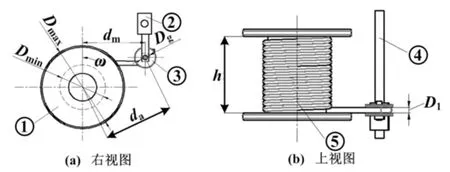
图1 收排线系统主结构示意图

工字轮收线机的相对运动具体表现如下。工字轮以角速度ω作单向旋转运动，导线轮随排线架沿工字轮轴向作往复运动。以工字轮一侧边作为导线轮初始位移原点，当传感器检测到导线轮移动至工字轮另一侧边处或导线轮的位移达到h后，排线架经过延时时间τ后换向，然后移动至工字轮的另一边。一旦预设的换向位移hp大于或小于实际换向位移h，在工字轮边缘就会出现堆积或漏绕现象。在此期间，可以通过检测线材张力变化所反映的绕线平整度变化，确定工字轮边缘处是否出现凹陷或凸起现象，进而决定下一次绕线周期的换向点位置，从而起到调整作用。对工字轮的另一边作同样处理，周而复始，直至满盘。

在收线过程中，受张力导致的线材滑落、线材本身的摩擦因数、工字轮加工精度和换向点位置误差等因素的影响，难以对收线机绕线过程进行精确建模。在这个过程中，张力的变化又涉及绕线半径的变化，使建模过程成为三维建模，无疑为研究工作增加了更多难度。同时，现有排线换向控制中急需解决PID参数整定问题，因此需要一种更智能的控制算法，以适应复杂的生产环境。

2 数学建模及模糊PID控制器设计

2.1 数学模型

基于现有问题，本文忽略绕线过程中的不确定因素，仅考虑线材的绕线成型轨迹，建立收线机绕线轨迹数学模型。经试验证明，该模型能在一定程度上反映绕线规律，具有一定的研究价值。

为方便叙述，设在实际收线过程中，线材与工字轮的切点为A点、与导线轮的切点为B点，两点都是动态的，且A点的轴向位移即为工字轮收线缠绕轨迹的轴向分量，B点的轴向位移即为导线轮的轴向位移。在工字轮收线过程中，想要达到密集收线，那么工字轮每转一圈,就要求排线架移动一个线径的排线距[8]。因此，有收线速度与排线速度关系式：

(1)

式中:vg为导线轮轴向移动速度，即排线速度；vr为工字轮旋转线速度；Dr为工字轮卷绕直径。

A点与B点在工字轮端面投影之间的距离dm有：

(2)

工字轮收线机的绕线示意图如图2所示[9]，图中粗实线代表缠绕的丝线。将缠绕曲面沿轴向展开，因为滞后角δ不变，根据三角形相似原理，有：

(3)

(4)

得到A点的轴向位移微分方程为：

(5)

式中：sf为A点实际轴向位移；dp为B点轴向位移与A点实际轴向位移之差；sr为工字轮旋转线位移；sg为导线轮轴向位移。

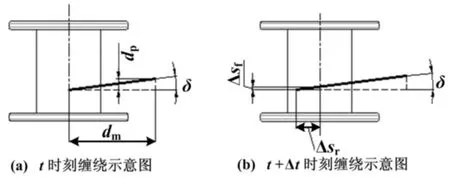
图2 绕线示意图

当排线位移达到预设换向位移hp时，如果排线装置立即回转，在工字轮上、线与工字轮边之间会出现少绕和漏绕的现象。所以，需要在换向回转上叠加延时。所需最小延时τ为：

(6)

由于实际绕线过程中存在非线性因素，使得难以由单圈线圈的轴线位移变化去描述线材的径向高度变化，所以在数学模型中较难用线材的径向高度去计算平整度。但是在实际生产中，因为张力的存在导致线材滑落，使得由换向点位置误差产生凹陷或凸起现象。线径高度由工字轮最边缘处向中心处呈递进坡度趋势变化,如图3所示。

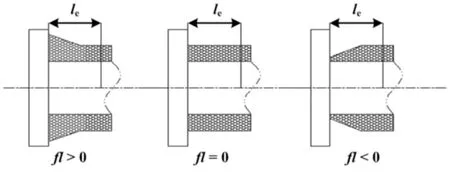
图3 工字轮边缘侧平整度示意图

图3中：黑色部分代表绕线线材剖面；白色框图代表工字轮；le为平整度计算取样距离；fl为边缘处绕线平整度。由此证实了通过检测平整度调整换向点位置，最终实现平整度调节这个方案的可行性。

鉴于此，考虑到工字轮绕线的平整度还与在一个换向周期内、一定边缘距离上绕线的圈数存在对应关系。本文以工字轮一侧的换向过程为例，将对线径高度变化的计算转化为在边缘处一定距离le上所绕线圈数变化的计算，并将实际绕线圈数cf与平整状态最大允许绕线圈数cmax之差和最大允许绕线圈数作比较，其差值作为边缘处的绕线平整度fl。fl>0，代表绕线凸起；fl=0，代表绕线平整；fl<0，代表绕线凹陷。假设排线器往返一次为一个周期，则第k个周期绕线平整度flak为：

(7)

式中：le为试验选定的取样距离，可以根据实际需求来赋值；Te为轨迹点A在le上往返所运行的时间。

第k个周期完成后的累加平整度flk为：

(8)

位移速度计算公式为：

(9)

假设排线装置位移初始为0，hp为预设换向位置，排线装置速度vg初始方向为正，则其速度方向判定算法如下。

Input：vg,sg，hp

Output：vg

Begin：

if {(vg>0 andsg>hp)or(vg<0 andsg<0)}

vg=-vg

End

2.2 模糊PID控制器设计

模糊控制算法是人工智能控制的一大分支，是通过计算机来实现人类自然语言描述控制规则的算法。此算法不需要知道系统的数学模型，即可以对系统进行有效控制，具有响应快、超调小等特点[10]。

本文模糊控制器以误差e和误差变化率ec作为输入，以PID控制参数kp、ki、kd作为输出。将输入输出对应论域划分为七个层次：[正大、正中、正小、零、负大、负中、负大]，对应[PB、PM、PS、ZE、NS、NM、NB]。隶属度函数采用三角形隶属度函数，然后使用面积重心法进行模糊处理。根据模糊控制规则的基本思路，结合实际生产经验，经分析、归纳和总结，制定如表1所示的PID参数模糊控制规则。

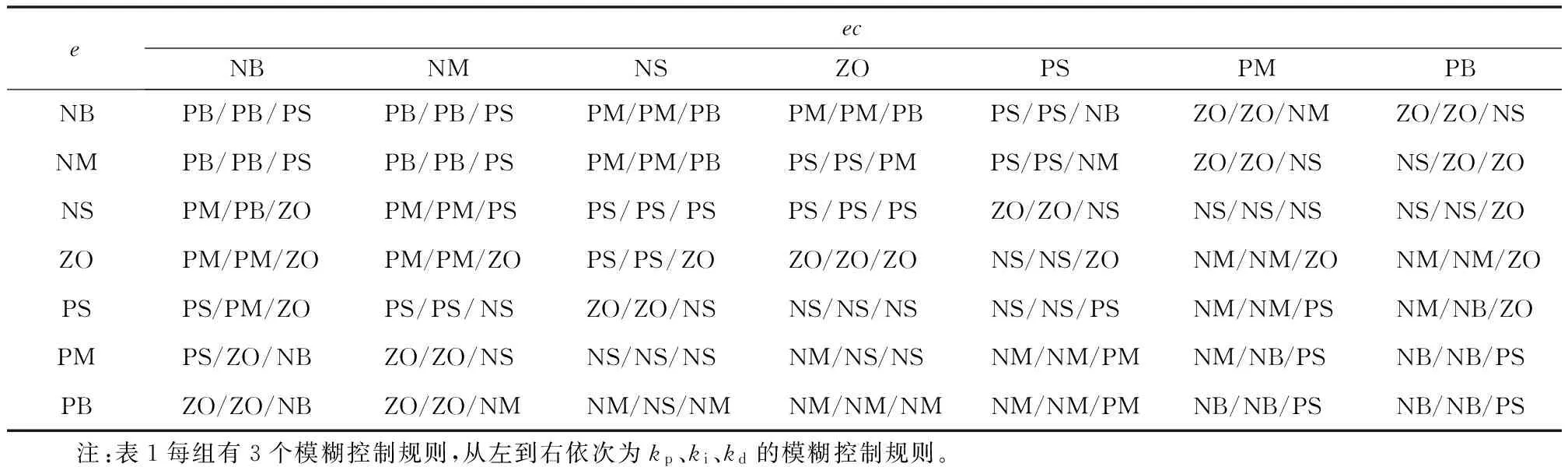
表1 PID参数模糊控制规则表

最后，设计如图4所示的基于模糊PID控制框图。模糊控制器以平整度误差e和误差变化率ec作为输入，以PID控制参数kp、ki、kd作为输出。图4中，rin表

示理想平整度。并结合以实际生产经验为基础而制定的模糊控制规则表，完成对PID控制参数的在线实时整定[11-12]。

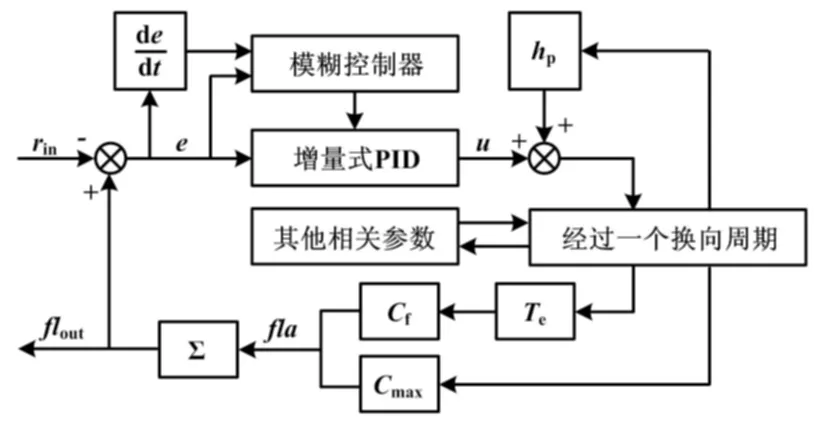
图4 模糊PID控制框图

3 仿真与试验

在Matlab2012a平台上，利用式(1)～式(9)及

各种补充公式和各种仿真模块，结合图4控制框图，配合传统PID控制、基于RBF神经网络PID控制算法以及基于模糊PID控制算法等，分别建立工字轮收线机排线控制模型。

本研究采用华方机电科技有限公司HF-SS770A型号收线机参数，工字轮型号为WS50，具体参数如表2所示。取排线初始位置为工字轮一内侧边处，其位移sg=0 mm，A点轴向初始位移sf=0 mm，平整度取样距离le=7 mm。经计算可得，对于工字轮的任意一侧而言，该工字轮由空盘到满盘的换向周期数最大为100。同时，将hp=224 mm时，经过一个换向周期后得到的绕线平整度标准化为1。

表2 收线机参数表

3.1 常规PID控制算法试验

常规PID控制算法以其简单、有效的特性，被广泛应用于工程实践中。基本PID控制算法经离散化，可得到位置式PID控制算法；位置式PID控制算法经变形，可得到增量式PID控制算法[13]。本文首先使用增量式PID控制算法对本文模型进行验证性系统分析。

本文模型在单纯的比例环节(proportional,P)控制下，其阶跃响应会出现等幅震荡的效果，试验结果如图5所示。

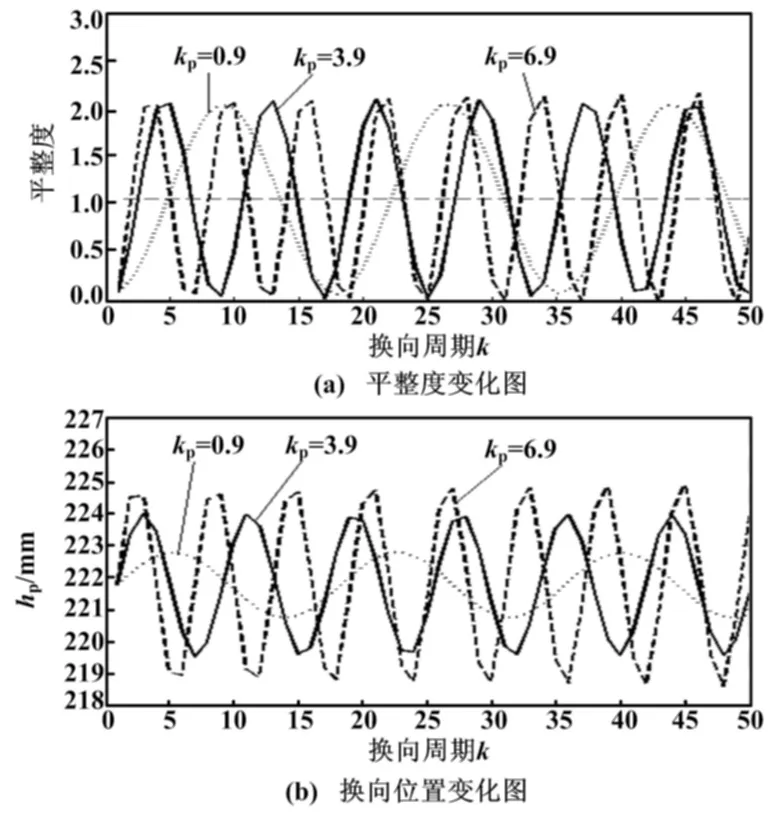
图5 常规PID控制算法试验结果图

由图5(a)可知，平整度曲线随着kp在一定范围内增大，震荡周期缩短，但其震荡幅度基本不变。再结合图5(b)可见，当平整度小于期望值时，系统调整换向点位置增大，使平整度逐渐增大；当平整度大于期望值时，系统调整换向点位置减小，使平整度逐渐降低。

另外，结合图5(a)、图5(b)来分析，平整度曲线及换向点位置曲线出现等幅震荡形式的原因如下。本文的被控量本身是一个累加参数，所以当平整度由原平衡状态调整到期望值时，换向点恰好达到最大偏移位置。此时，因为平整度误差为零，导致换向点位置将在下一时刻以最大偏移量作为输出，造成新的平整度误差，并以此循环下去。

而完整的PID控制试验表明，促使控制曲线收敛的关键因素不再是比例环节，而是微分环节。在具有相同kp、ki和不同kd的PID控制下，平整度的变化如图6所示(其中：kp=3.9，ki=0.5)。由图6可知，控制曲线收敛，并且在一定范围内随kd参数增大，收敛速度加快。但当kd超出一定值后，效果会变差。

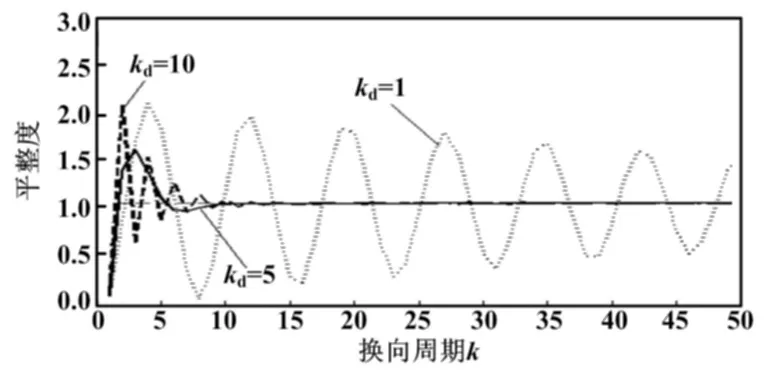
图6 不同kd的PID控制下平整度变化图

本文通过一定数量的试验，对PID控制的三个参数进行了整定。在综合考虑超调量及调节周期的前提下，得到PID参数的近似最优解：kp=3.9，ki=0.5，kd=5。在此参数的控制下，其控制曲线如图6中的实线所示，其超调量为58.57%，九个调节周期后到达稳态值(本文误差带范围取±5%)。

单P控制试验表明，本文模型可以实现对平整度的控制；单P控制不适用于收线机换向控制系统。完整的PID控制试验表明，促使本文系统控制曲线收敛的关键因素是微分环节。其原因是：微分环节有一定的预测性，产生超前的控制作用，能够调整曲线收敛；但微分环节对噪声干扰有放大作用，随着微分环节作用的增强，其鲁棒性将会变差。

考虑到排线换向控制系统本身的特性，使得现场进行PID参数整定成为一项繁杂又耗时的工作，这就需要系统具有能根据现场情况对其参数进行线上自整定的功能。为此，本文引入了两种目前主流的智能整定PID参数的算法——基于神经网络PID控制算法和基于模糊PID控制算法，实现了两种算法在本文模型上的应用，并对整定效果进行了分析。

3.2 基于RBF神经网络PID控制算法试验

基于RBF网络整定的 PID控制由 RBF神经网络辨识器和 PID控制器两部分组成。RBF神经网络辨识器通过被控对象的输入、输出数据，辨识出被控对象的近似模型,并以此代替被控对象的输入、输出关系[14-15]。 PID控制器的参数通过 RBF神经网络辨识器实现自适应整定。

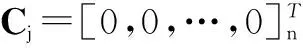
对单P控制阶跃响应曲线进行整定，其整定曲线如图7中的全参整定曲线所示。由图7可知，曲线能在较短的周期内收敛，并且其超调量为116.43%，调节周期数为16，但在最后出现了稳态误差。这是因为本文系统中的被控对象Jacobian信息[16]，即对象的输出对控制输入变化的灵敏度一直为负值，导致由梯度下降法对积分环节ki的整定过程一直是向下整定；而ki值本身又为非负值，最终导致积分环节一直为零，失去了调节作用，使得最后出现了稳态误差。

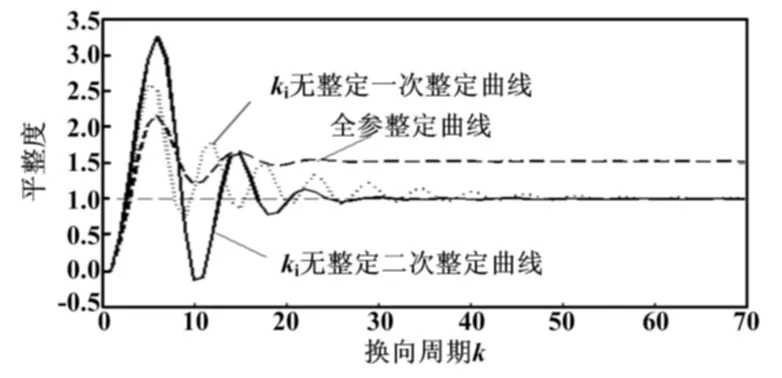
图7 基于RBF网络PID控制平整度曲线

因此，本文取消了RBF神经网络对于积分环节的整定作用，只使用其对kp、kd进行整定。ki通过试验调试进行赋值，ki=0.5、kp=3.9、kd=0。再次进行RBF网络整定试验，结果如图7中的ki无整定一次整定曲线所示。其超调量为159.76%，调节周期数为46。因为积分环节的加入，使得系统控制超调量有所增加，并表现出一定的滞后性；调整时间相较于全参整定试验有所增加，但依然表现出一定的整定能力。

以第一次整定的PID参数值作为初值，进行第二次整定，结果如图7中的ki无整定二次整定曲线所示。其超调量为225.71%，调整时间为24个周期。可见，其调整周期缩短了22个周期，但是其超调量增加了65.96%。这是因为神经网络逼近输出曲线，本身必然存在一定的滞后性，再加上随着过渡周期的缩短，提供给网络用于自身整定的数据减少，由此会产生网络自身逼近输出曲线的偏差，使得有可能出现超调增大的现象。

综合图7中的三条曲线可知，随着整定次数的增加，曲线的调节时间越来越短，但是超调量越来越大。由此表明，基于RBF神经网络PID控制算法对本文收排线控制系统具有一定的整定作用，可以为PID参数的整定提供指导，但其最终整定效果并不太理想。

3.3 基于模糊PID控制算法试验

对单P控制阶跃响应曲线进行基于模糊PID参数整定，试验结果如图8中的一次整定曲线所示。其超调量为103.33%，调整时间为28个周期。与基于RBF神经网络的ki无整定第一次参数整定试验结果相比，基于模糊PID参数整定的超调量降低了56.43%，调节周期缩短了18个换向周期，整定性能更强。

利用基于模糊PID控制算法进行了第二次整定，整定结果如图8中的二次整定曲线所示。其超调量为52.38%，调节周期为12个周期。其效果与RBF神经网络PID控制算法的二次整定试验结果相比，体现了更大的优势。而对比于本文中的PID控制近似最优解，其超调量降低了6.19%，但调节周期增加了3个。

使用基于模糊PID控制算法进行了第三次整定试验，结果如图8中的三次整定试验曲线所示。其超调量为43.33%，调节周期数为9；与PID控制的近似最优解具有相同的调节周期，但是超调量降低了15.24%。

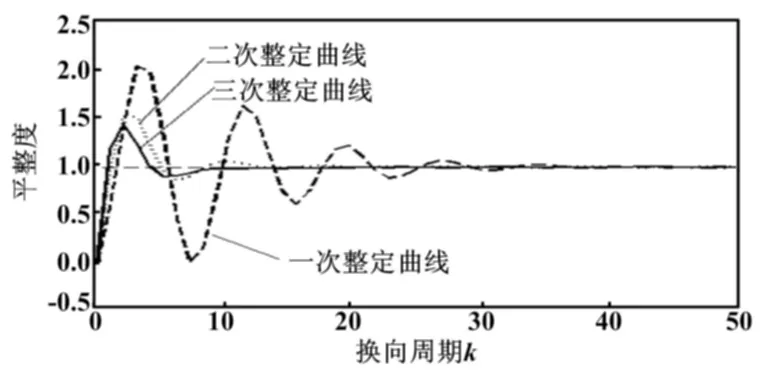
图8 基于模糊PID控制平整度曲线

3.4 试验结果比较分析

整理各控制算法的控制效果如表3所示。其中，PID代表PID控制算法近似最优解，RBF1、RBF2分别代表RBF神经网络ki无整定一次整定试验，ki无整定二次整定试验；Fu1、Fu2、Fu3分别代表模糊PID控制算法的一次整定试验、二次整定试验、三次整定试验。RBF神经网络PID全参整定试验，因最后出现稳态误差而失去比较价值，未被收入表中。

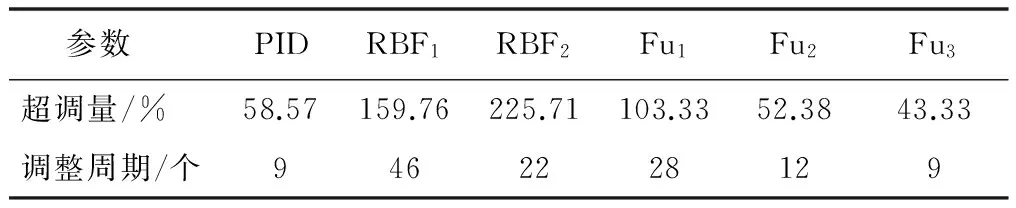
表3 控制效果表

结合表3数据可见，针对收线机排线换向控制系统，基于模糊PID控制算法，对比基于RBF神经网络PID控制算法，体现了更强的整定效果和整定效率。并且，基于模糊PID控制算法，通过自身的不断整定，可以达到最优解，表现出较强的连续整定能力及鲁棒性，即使其整定结果依然存在一定的极限值。当调整周期缩短到一定程度后，会因可用于进行整定的数据点过少，导致其失去整定作用。但在本文中，该算法经过三次自整定后的控制效果已经超过了经试验调试得到的近似最优解，体现了较强的整定能力，为收排线系统的控制算法升级提供了参考。

4 结束语

本文针对收线机收线平整问题，重点分析了排线装置的换向控制问题，建立了排线换向控制模型，并利用常规PID控制算法对其进行了系统仿真分析；针对PID控制参数整定的问题，进行了基于RBF神经网络PID控制算法和基于模糊PID控制算法在本模型上的对比试验。

本文模型能在一定程度上正确反映收线机排线换向控制过程。排线换向控制系统是一个累加量的控制系统，因此，PID的微分环节对于控制的收敛起关键性作用。针对PID参数整定问题，基于模糊PID控制算法相较于基于RBF神经网络PID控制算法在排线换向控制系统中更为适用。综上所述，本模型可以为收线机排线换向控制系统的进一步设计与优化提供参考依据和理论支撑。

[1] 陈锦海,梁庆华,王石刚. 实现复杂运动的高速排线凸轮机构优化设计[J]. 机械设计与研究,2009,25(3):19-21.

[2] 李乐,李慧鹏,石阳. 绕线机的多轴同步控制算法研究[J]. 测控技术,2014(2):87-90.

[3] 徐展. 电机精密同步控制技术的研究与应用[J]. 电子科技大学学报,2008(S1):16-18.

[4] ZHANG X,WEI H,WANG M,et al. Research on computer control system of close precision winding[C]//INDIN 2008 6th IEEE International Conference on Industrial Informatics. IEEE,2008:910 - 914.

[5] HUO Y,LI Z,QIU J. Adaptive control of industrial winding multivariable process system[C]//2012 International Conference on Machine Learning and Cybernetics (ICMLC). IEEE,2012:890 - 893.

[6] 周顺桃,黄友锐. ZS05型光纤着色机自动排线控制系统的设计[J]. 光纤与电缆及其应用技术,2013(2):29-32.

[7] RODRIGUEZ A,VRANCX P,NOWE A,et al. Model-free learning of wire winding control[C]//Control Conference (ASCC),2013 9th Asian. IEEE,2013:1-6.

[8] 徐贺,惠晶,陈俊. 光纤着色精密卷取排线控制系统[J]. 电气传动,2009(3):58-61.

[9] 张吉月,纪文刚,张立新. 基于PLC的焊丝自动排线技术的研究[J]. 微计算机信息,2008(16):57-59.

[10]陈家伟,陈杰,陈冉,等. 变速风力发电机组自适应模糊控制技术[J]. 中国电机工程学报,2011,31(21):93-101.

[11]冯冬青,任雪梅. 模糊PID在网络控制系统中的仿真研究[J]. 自动化仪表,2013,34(1):61-63.

[12]孙莉,赵志光. 模糊PID控制器在水泥回转窑上的应用[J]. 自动化仪表,2014,35(1):26-29.

[13]刘素芹,刘新平,戚平,等. PID与模糊控制算法的比较及其改进[J]. 控制工程,2003,10(1):51-52.

[14]MENG Y,ZHIYUN Z,FUJIAN R,et al. Application of adaptive PID based on RBF neural networks in temperature control[C]//2014 11th World Congress on Intelligent Control and Automation. IEEE,2014:4302-4306.[15]ZHOO Y,DING Q. Study of PID temperature control for reactor based on RBF network[C]//2012 IEEE International Conference on Automation and Logistics (ICAL). IEEE,2012:456-460.

[16]WANG S,LI B,GENG Q. Research of RBF neural network PID control algorithm for longitudinal channel control of small UAV[C]//2013 10th IEEE International Conference on Control and Automation (ICCA). IEEE,2013:1824-1827.

Modeling and Simulation Analysis of the Wire Guiding and Reversing Control of Spooler

Aiming at the problems of spooler existing in guiding and reversing control of the taking up process ,the physical model of the guiding and reversing control is given,and the dynamics model of the process is set up. The simulation analysis of verification of conventional PID control algorithm for the mathematical model is conducted,and the contrast analysis of the control algorithm based on fuzzy PID and control algorithm based on RBF neural network PID on this model is implemented. The results show that the built model can simulate the process of spooler,and the algorithm based on fuzzy PID is more effectively to improve the reversing effect; the simulation data can provide reference basis for designing and optimizing the guiding and reversing control system of the spooler.

Spooler Dynamics model RBF neural network Fuzzy PID algorithm Reversing control Mathematical modeling Parameter tuning Simulation

国家自然科学基金资助项目(编号：61170121、61202312)。

王培斌(1989—)，男，现为江南大学计算机技术专业在读硕士研究生；主要从事计算机应用技术的研究。

TH-39;TP391

A

10.16086/j.cnki.issn 1000-0380.201608018

修改稿收到日期：2016-02-25。