数学方法好，解题没困扰——几种典型的高中数学解题方法例析

筅江苏省常熟市浒浦高级中学　郑晓晴

数学方法好，解题没困扰——几种典型的高中数学解题方法例析

筅江苏省常熟市浒浦高级中学郑晓晴

高中数学题型多变，表面看来难度大，深度广，很容易让学生望而生畏，要想消除学生的这种顾虑，就要从解题方法入手，潜心研究，不断反思，总结方法.要懂得根据题设的相关知识，提出灵活的设想，寻找巧妙的解题方案.方法恰当事半功倍，方法不对收效甚微，所以要学好高中数学必须要重视解题方法的研究.本文将着重进行以下几个方法的介绍.

一、转换法

高中数学一种不可或缺的解题方法就是转换法.这种方法的解题思想是把未知问题转化为已知问题.适合解决难易程度较高的题型，稍具难度的问题和基础知识的联系都是不明显的、间接的、复杂的，能够灵活运用这种方法对学生的想象力和创造性思维是不小的挑战.这种方法关键一步是将所求式（未知问题）朝着已知的方向进行合理的变形，好的转化方法可以把不熟悉的问题转为熟悉的，把不规范的问题转为规范的，复杂的问题转为简单的.比如，对于有理分式的题可以运用转化方法将分式化为整式，广义分式也可以将一元函数转化为二元函数求积分，然后解答起来就简单容易了.

例1若x、y、z∈R＋且x＋y＋z＝1，求∈的最小值.

分析：由关键性的已知条件x＋y＋z＝1我们联想到：将所求式变形转化为含代数式x＋y＋ z，或者运用均值不等式后含xyz的形式，这样就将所要求的未知问题转化为已知问题.答案很快就明了了.本题先通分，再整理分子，最后拆分.将求

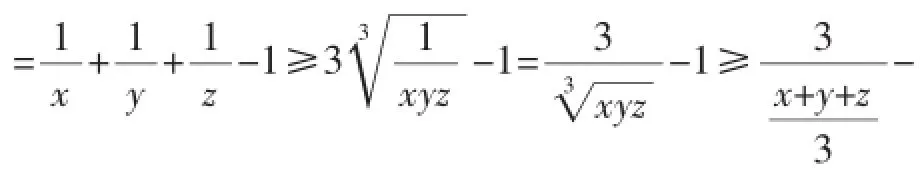
转化意识的形成不是一蹴而就的，需要我们在解题中不断的应用，不断的训练，久而久之强化这种转化思想，培养解决数学问题的应变能力，提高数学素质.

二、反证法

“若肯定定理的假设而否定其结论，就会导致矛盾”.这是法国数学家阿达玛对反证法解数学题的精辟概括.逻辑性与规律性兼容是高中数学的基本特点，能从题目中很容易就找到证明条件的情况少之又少，当我们从正面入手很难找到切入点的时候，不妨换一种思维方式，想方设法从它的相反方向考虑寻找突破口.具体地说，首先否定原命题，再把这个经过否定的命题作为一道新题的已知条件，在这个已知条件下进行正常的推理，推出的结论与我们公认的已知条件、已知公理、定理、法则或者已经被证明为正确的命题等相矛盾，根据这个矛盾的结论就可断定最初的假设不成立，进而肯定了原命题的结论，这就是反证法.运用反证法主要分为以下几个步骤：①假设：仔细阅读题目，理清原命题的条件和结论是什么（为了防止出现错误，可以在草纸上列出来），理清头绪后作一个与命题结论相反的假设，也就是结论的反面成立.②求证：以上面的假设为已知条件出发，运用正常的推理法进行求证，从而得到矛盾的结果是成立的.③最后一步需要推理一下：产生上面矛盾结果的原因是第一步的假设本身就是假的，而第二步求证假设的结果也不真，这就间接地证明原命题是真实的，从而完成原命题证明，它是一种间接证明的方法.

例2求证两条直线a，b中的一条与平面α相交，则另一条也和平面α相交.

证明：这类题我们完全可以用反证法来解决，假设直线a与平面α相交，a、b互相平行，b也与平面α相交，假设b不与平面α相交，就必然形成了两种情况：

①b在平面α内，由a平行于b，a不属于平面α，a平行于平面α，与题设相互矛盾.

②b∥α，可过b作平面β，设β∩α=c，则b∥c.而b∥a，则a∥c，同上可得a∥α，与题设a与α相交矛盾.

因此b和α只能相交.

在同一思维过程中，真相只有一个，既然b在平面α内和b∥α已经为假，那么原结论b也和平面α相交就一定为真.反证法另辟蹊径，反其道而行之，要求学生有很强的逆向思维能力，根据题的特点，对症下药，准确假设，细心求证，科学推理，任何一步都不能有纰漏，否则前功尽弃.所以要求学生在做题时，认真审题，审慎考虑，理清头绪，大胆尝试，否则起不到事半功倍的作用.

三、数学归纳法

证明与自然数N有关的命题是高中数学常见的题型，数学归纳法针对这种问题最适用.归纳法是由一系列有限的特殊事例得出一般结论的推理方法，应用非常广泛，一般来说，与正整数有关的一些恒等式、不等式、整除性、数列的通项及前n项和等问题都可以采用此种方法，它条理清晰，操作简单，很容易接受.要熟练地掌握数学归纳法，必须准确地把握解题步骤，归纳法分为以下几步：第一步，验证n＝n0时命题成立，这是基础性的一步，为后面的归纳做铺垫；第二步，若n＝k（k≥n0）时命题成立，证明当n＝k＋1时命题也成立，这是关键性的一步，为后面的归纳作递推；最后，得出结论，命题对从n0开始所有的正整数n都成立.两个步骤（同样重要），一个结论，缺一不可.

例3求证：12＋22＋32＋…＋n2＝n（n＋1）（2n＋1）.

证明：①当n＝1时，左边＝1，右边＝1，等式成立.（归纳奠基）

②假设n＝k时等式成立，即12＋22＋32＋…＋k2＝ k（k＋ 1）（2k＋1）.

由①②可知原等式对于任意n∈N*都成立（结论）.

评析：第一步是求证n取第一个值时等式是否成立，第二步在假设n＝k时，一定要写出对应的表达式，证明n＝k＋1时，一定要用到归纳假设.第二步证明的关键要看左右两边的项和证明的目标，合理利用一凑假设，二凑结论的证明技巧.为了做题时不缺少步骤，我们可以记住这样一个口诀：递推基础不可少，归纳假设要用到，结论写明莫忘掉.

四、图解法

数学少不了图形，数学图形直观形象，清晰明了，还能把数学问题的条件、结论及它们之间的关联精确地反映出来，我们要巧妙地利用图形的这一特点，它也是解决数学问题的又一重要技巧.解决数学问题不能手懒，有时只靠头脑想像还是缺乏直观性，容易忽略某个已知条件，而绘制图形摆在眼前，所有已知条件跃然图中，借助对几何图形的有效分析，得出文字数学的结论（将所研究的代数问题转为研究其对应的几何图形），实现抽象文字表述到具体形象展现的转化，达到数与形的密切结合，科学渗透，我们给这种方法起个名字叫图解法.图解法的特点就是将许多抽象的数学概念和数量关系以图形的形式直观地展现给学生，借助学生对图像的敏感，启发学生的思路，寻找解题的关键，以便获取更加准确的答案.图解法是数形结合在数学解题过程的集中性体现，由“形”获取“数”的方法.

例4已知偶函数y=f（x）（x∈R）满足f（x+1）=f（x-1），且x∈［0，1］时，f（x）=x，则方程f（x）=log3x的解的个数为（）.

A.1个B.2个C.3个D.4个

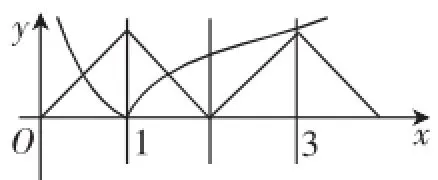
图1　

解析：用图解法.根据题意，函数最小正周期为T=2，则画出图像（图1），由图像观察得知，符合题意的选项是C.

图解法既分析其数与量之间的关系，又揭示其几何含义，避免了文字的枯燥，展现了图形的魅力，使数量关系和图形紧密地联系起来，不仅能够对高中生的数学知识进行整合，还能够增强对他们的创新性思维的培养.这种方法的应用广泛并贯穿高中数学学习的全过程，我们要在实践中不断地加以练习，熟悉识图技巧，形成良好的数学思维习惯，掌握其内涵，领会其精髓，培养学生利用图形解决问题的能力，解决数学难题对学生的困扰，让学生在数学题海中自在的遨游.F