浅谈向量在几何中的运用

筅江苏省泰兴市第二高级中学　周余峰

浅谈向量在几何中的运用

筅江苏省泰兴市第二高级中学周余峰

向量是一个新的数学知识章节，自从2003年第一次进入新课程教材，向量承担着越来越重要的工具性作用.向量既具有代数的运算特点，还有几何的本质特征，因此向量渐渐成为既能区分学生思维能力又能考查学生运算水平的重要知识点，它的工具性作用在中学数学教学中也越发明显.

怎么才能使用好向量的工具性作用呢？向量的工具性作用，又如何展示向量的本质特征呢？中学数学中所涉及的平面向量，以及平面向量的基本特征，包括平面向量的基本运算，这些都是工具性的具体体现.近年来，随着教学中对向量本质的认知越来越深刻，向量问题的难度有逐年加大的趋势，这就需要教师不断引导学生，既要加深向量的运算水平也要提高对向量几何意义的一些理解.近代中学数学泰斗吴文俊先生是这样描述向量的：我们利用向量运算，可以把我们以前无法解决的很多几何问题仅仅通过运算就可以解决了，这是向量工具代数化的体现；反过来，很多复杂的代数问题我们也通过向量的几何含义轻松解决.本文将从向量解决几何问题的视角，谈一谈它在解决几何问题中的工具性作用.

一、向量的核心知识

对于教学而言，下面知识是向量最基本的核心知识：第一，向量加减法，它把向量加法和减法的几何含义通过平行四边形法则和三角形法则充分地展示了出来；第二，向量的数乘运算，充分地展示了向量的共线性；第三，平面向量基本定理，这是平面向量非常核心的知识，对这一定理知识掌握得好坏，可以大大区分学生对于向量知识是否有本质的理解；最后，从物理功这样的概念中类比得到的平面向量数量积，是中学数学向量运算的最后一个知识点，也是最重要的知识点，如极化恒等式等都是解决向量几何问题的有力武器.对比平面向量和空间向量，其工具的核心有：

知识点平面向量空间向量多点共线条件+yO筅平面内任意一点O和不重合的两点A、B，若O筅筅P=xO筅筅A筅B（其中x+y=1），则P、A、B三点共线对空间任一点O和不共线的三点A、B、C，若满足O筅筅P=xO筅筅A+ yO筅筅B+zO筅筅C（其中x+y+z=1），则P、A、B、C四点共面向量基本定理如果e1、e2是平面内的两上不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1、λ2，使a=λ1e1+λ2e2如果三个向量a、b、c不共面，那么对空间任一向量p，存在一个唯一的有序实数组x，y，z，使p=xa+yb+zc向量的坐标运算已知a=（x1，y1），b=（x2，y2），则a+b=（x1+x2，y1+y2），a-b=（x1-x2，y1-y2），a·b=x1x2+y1y2，a∥b圳x1=λx2且y1=λy2（λ∈R）已知a=（a1，a2，a3），b=（b1，b2，b3），则a+b=（a1+b1，a2+b2，a3+b3），a-b=（a1-b1，a2-b2，a3-b3），a·b=a1b1+a2b2+a3b3，a∥b圳a1=λb1且a2=λb2且a3= λb3（λ∈R）夹角和距离设a=（x1，y1），b=（x2，y2），则a=x21+y21姨，b=x22+y22姨，cosθ=x1x2+y1y2x21+ y21姨x22+y22姨；如果表示向量a的有向线段的起点和终点的坐标分别为（x1，y1）和（x2，y2），那么|a|=（x1-x2）2+（y1-y2）2姨设a=（a1，a2，a3），b=（b1，b2，b3），则a=a21+a22+a23姨，b=b21+b22+b23姨，cos〈a，b〉= a1b1+a2b2+a3b3姨a21+ a2 2+ a23姨b21+ b2 2+ b23；已知A（x1，y1，z1），B（x2，y2，z2），则|A筅筅B|=姨（x2-x1）2+（y2-y1）2+（z2-z1）2

二、向量在解析几何中的渗透

众所周知，解析几何是中学数学教学的难点和重点.解析几何问题，如果只从代数化的角度去思考，其运算量非常之大，若能从向量角度去思考，结合向量具有几何特征这一特点，可以大大简化问题的运算.教师在教学中应该多加引导，让学生明白向量工具性的作用，向量不仅仅只能运用于向量章节，工具性的作用使它可以运用于任何具备代数和几何特征的知识中.

问题1（共线问题）过抛物线y2=2px焦点F的一条直线与它交于两点P（x1，y1），Q（x2，y2），经过点Q作抛物线准线的垂线，垂足为点M，设抛物线的顶点为O.求证：

（Ⅰ）y1y2=-p2；

（Ⅱ）三点M、O、P共线.

说明：运用向量证明共线，无需平面几何式烦琐的作图过程，也没有一味的强行计算，通过坐标向量以及向量共线的充要条件，轻松快捷，体现了向量工具性的作用.

问题2（夹角问题）已知一个圆的直径的端点是A（x1，y1）、B（x2，y2），求证：圆的方程是（x-x1）（x-x2）+（yy1）（y-y2）=0.（教材课后习题第82页习题3）

传统解法：因为直径的端点为A（x1，y1）、B（x2，y2），

向量优解：设P（x，y）是此圆上与点A、B都不重合的一点，则若P（x，y）是与点A或点B重合的点，则所以=0，从而（

说明：解析几何中对于角的求解，更多的是利用余弦定理或者正切到角公式，前者运算烦琐，后者已被教材删减，而在向量中要解决钝角问题即向量不共线且数量积为负值即可.类似的问题在高考中也出现过，请看下面的变式：

解析：F1，设P（3cosθ，2sinθ）.因为∠F1PF2为钝角，所以-2sinθ）·1<0，解得-故点P横坐标的取值范围是

三、向量在立体几何中的运用

对于利用向量解决立体几何问题，在我们今天看来是一件非常平常不过的事情.曾几何时，立体几何是中学数学的一个难点，很多空间几何问题，从传统法的角度要想找到线面角、二面角、点面距离极为困难，因为有了空间向量了的引入，将以往这些难点变得易于掌握和解决.

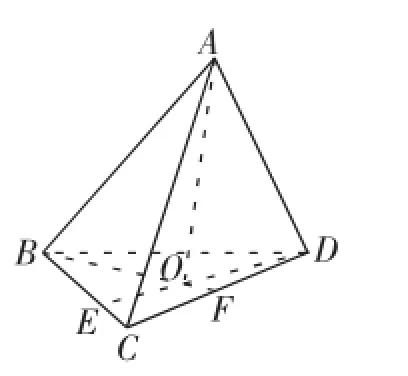
图1　

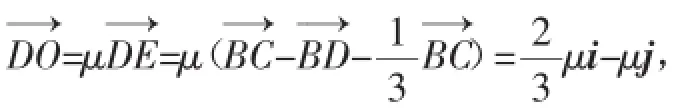
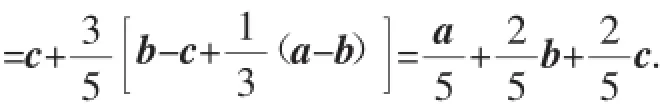
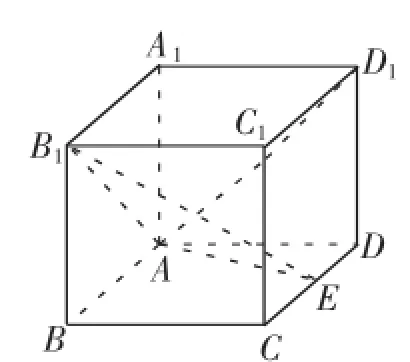
图2　

说明：向量有自由向量和坐标向量，相比而言，自由向量的使用度更为广泛，也更为方便.类似于平面向量基本定理，在空间任何一个向量的分解都可以利用空间向量基本定理去实现，这样就把所有的问题归结为向量的代数运算，从而轻松地将立体几何问题转化为代数运算.

问题4（坐标向量解空间几何）如图2，在长方体ABCDA1B1C1D1中，AA1=AD=1，E为CD中点.

（Ⅰ）求证：B1E⊥AD1.

（Ⅱ）在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由.

（Ⅲ）若二面角A-B1E-A1的大小为30°，求AB的长.

解析：（Ⅰ）证明：以点A为原点建立空间直角坐标系，设AB=a，则A（0，0，0），D（0，1，0），D1（0，1，1），E，

（Ⅱ）假设在棱AA1上存在一点P（0，0，t），使得DP∥平面B1AE，则D11P=（0，-1，t）.

设面B1AE的法向量为n=（x，y，z），有，取x=1，可得n=，要使DP∥平面B1AE，只要，则

又DP埭平面B1AE，所以存在点P使DP∥平面B1AE，此时AP=

（Ⅲ）连接A1D，B1C，由长方体AA1=AD=1，得A1D⊥AD1.

因为B1C∥A1D，所以AD1⊥B1C.

由（Ⅰ）知，B1E⊥AD1，故AD1⊥平面DCB1A1.是平面DCB1A1的一个法向量，而=（0，1，1），则cos<

因为二面角是30°，所以AB=2.

说明：相比问题3，问题4是坐标向量的体现，我们知道坐标向量最大的好处是正交分解的引入，是所有的向量均可用纯代数的方式来进行运算，这也是我们现阶段空间几何教学中使用频率最多的方式方法.可以这么说，因为有了空间向量大大简化了我们对于角和距离的求解，将很多极难的空间想象问题转换为代数求解问题，将立体几何问题的求解向前推进了一大步.

总之，通过上述案例我们不难发现，如果仅仅从纯代数的角度去解决问题，势必消耗大量的运算，如果可以结合向量既有代数特征又有几何本质这样的工具性作用，那么解析几何、立体几何中的很多问题，我们都可以找到一个合适的切入点.举个通俗易懂的例子，就好比我们在较长的山洞中挖隧道，无论你从东往西挖还是从西往东挖都非常费力，如果我们既能从东往西，又能从西往东两者结合起来，不仅快速而且有效地打通隧道.因此，笔者也产生了以下两点思考：

第一，解决各种中学数学中的几何问题，从具备代数和几何双重特点的向量角度入手，往往让问题的解决来得轻快、简捷，既开拓了学生解决问题的视角，也提升了教师对于向量知识的更为深刻的理解.

第二，知识是发展的，要用发展的眼光来看待我们今天所学的知识.我们一直以为向量仅仅只是一个章节的内容，其实向量更具备了工具性的特征贯穿于中学数学教学的始终，如果能从这样的角度去看待向量，那么我们对于向量知识的理解和运用，能更上一层楼.限于水平，本文对向量解决几何问题的探讨还不够深入，请各位读者继续批评指正.

1.俞求是.高中数学新课程立体几何教学问题研究［J］.数学教学，2010（2）.

2.鲍建生，等.向量教学研究［J］.数学教学，2013（1）.

3.姜兴荣.探求解析几何解题思路的几种策略［J］.中小学数学，2013（7-8）.Z