倾听学生反思教学方能提高——由一道无法分离参变量的题引发的教学思考

筅江苏省高邮中学　季长征

倾听学生反思教学方能提高——由一道无法分离参变量的题引发的教学思考

筅江苏省高邮中学季长征

教师作为人生成长中重要阶段的引路人之一，有责任去倾听学生，倾听学生的需求，反思并改进自己的行为，成为他们人生成长的领路人，正如李政涛先生所言：“教育的过程是教育者与受教育者互相倾听与应答的过程.”有时倾听学生的一些做法，反思自己的教学会有不一样的收获.

一、倾听学生，问题产生

分离参变量是解决恒成立问题的一个重要方法，而不是唯一的方法.一天甲学生拿了下面的题目来问笔者，“已知函数（fx）=m（x-1）2-2x+3+lnx，m∈R，当m>0时，若曲线y=（fx）在点P（1，1）处的切线l与曲线y=（fx）有且只有一个公共点，求实数m的值.”

老师：你怎么考虑的？

老师：你怎么想到分离参变量的？

甲学生：我想到当函数图像有且只有一个公共点时可以用图像法，于是转化为直线与曲线的交点问题.

对啊，学生思路没有错啊，这可是自己平时教学中总结的啊.

老师：你把（x-1）2除过来有没有讨论x=1的情况？

反思：将陌生问题熟悉化，很棒！那么为什么甲学生会这样想，甲学生还说班上很多学生都是这么做的，都解到这解不下去了.他们也找到解答了，解答用的是分类讨论，这些话让笔者思考颇多，大部分学生酷爱分离参变量法，因为用分离参变量法，通常得到的是一个确定函数的不等关系，再用导数研究函数的单调性，往往是确定的，不需要讨论，笔者也这么认为，因为平时教学中笔者将这类题目的解法单一化，替学生总结这类题型的方法时过于武断，没有考虑其他方法.

二、反思教学，寻找原因

前段时间笔者在班上讲了这么一道题“已知函数f（x）=ax2-lnx（a为常数），若a<0，且对任意的x∈［1，e］，f（x）≥（a-2）x恒成立，求实数a的取值范围.”

学生一般的思路如下：因为f（x）≥（a-2）x在x∈［1，e］时恒成立，即a（x2-x）≥lnx-2x在x∈［1，e］时恒成立.

①当x=1时，此不等式恒成立，故此时a∈R.

令h（x）=x+1-lnx，x∈（1，e］，则h′（x）=1-在x∈（1，e］时恒成立.

故h（x）在x∈（1，e］时单调递增，从而h（x）>h（1）=2> 0，从而当x∈（1，e］时，g′（x）>0恒成立，故g（x）在x∈（1， e］时单调递增.所以g（x）max=g（e）

因为分类讨论的方法较为复杂，笔者也就一带而过，没有对分类讨论的方法作详细介绍.

反思：其实在很多试卷评讲课时，我们往往没有抓住第一时间去处理好这类问题的方法，机遇就这样稍纵即逝，殊不知，只讲分离参变量法会把学生的思路变得单一，一般题型还好，一旦遇到上面所谓分不了参的，学生就无从下手.若老师在评讲试卷时能认真讲一下分类讨论，学生也不会对一开始提出的问题无所适从.

改进讲法：除了分离参变量，有没有其他的解法呢？其实有的题目分离参变量的方法也是很好的.

设F（x）=f（x）-（a-2）x=ax2-lnx-（a-2）x.因为对任意的x∈（1，e］，f（x）≥（a-2）x恒成立，即F（x）≥0恒成立.

三、引入法则，解决问题

我们回到原题①，那常规思路应该怎么做呢？你们听完上面这道题能不能用分类讨论的方法呢？

在此可做总结，恒成立问题不一定是用分离参变量好，有时构造新函数，分类讨论也是很好的，要具体问题具体分析.既然笔者忽视对分类讨论解法的讲解，学生没想到.那上面这道题分离参变量真的就走不下去了吗？

老师：你分离参变量后，接着怎么做？

反思：这就是分参分不下去的根源.是不是就不能讲呢？竞赛课能讲，那平时的教学不能讲吗？如果学生平时习惯了分离参变量就走不下去了吗？

其实不然，我们今天引入一个新内容——洛必达法则，洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法.法国数学家洛必达在1696年的著作《阐明曲线的无穷小分析》中发表了这个法则，因此以他为命名.但一般认为这个法则是由瑞士数学家约翰·伯努利首先发现，因此也被叫作伯努利法则.

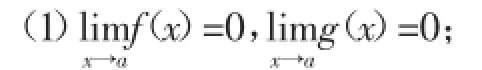
（2）在点a的某个去心邻域内两者都可导，且g（′x）≠0；

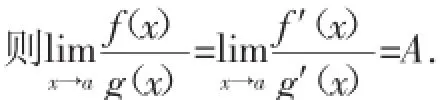
综上所述m=1.

这就带来个问题，洛必达法则有讲的必要吗？若讲的话，怎么讲呢？平时又不怎么用，讲了会不会违背高考考纲呢？笔者认为有讲的必要，数学的发展就是在遇到新问题后，解决新问题而产生新知识，应该说我们高中教学中不止一次出现可以用洛必达法则的，既然学生好理解，我们为什么不讲呢.怎么讲呢？不能突然说要讲洛必达法则，而是要抓住时机来讲.例如：在讲到类似f（x）=，当x→+∞，f（x）→0时，有的教师可能是用增长速度讲的，x+1的增长速度在x很大时比x2的增长速度慢.这样讲学生是好理解，但若能在这说出问题的本质岂不更好，其实我们可以用洛必达法则加以解释，它属于型不定式极限，这样既没有刻意去讲洛必达法则，也能让学生在正常学习中多学了一个知识，何乐而不为呢.其实学生在学物理时就已经接触到类似的问题，物理上说当正数x很小时，sinx近似等于x.用数学知识好理解所以正数x很小时，sinx近似等于x.

四、考试涉及，问题普遍

平时练习遇到这样的怪题，那高三模拟考试中有吗？有，而且不止一题.笔者就拿高三苏中三市调研考试中出现的一道题来说，巧的是笔者是网上阅这道题.此题为第19题共2问16分，第二问均分只有2.3分，为什么这么低，我们阅卷中发现第二问用分离参变量做的占到95%.为什么会这样呢？分参中绝大多数学生拿不到分数，为什么呢？我们先来看看题目：

已知函数f（x）=x+sinx.

（2）求实数a的取值范围，使不等式f（x）≥axcosx在上恒成立.

我们先来看看构造新函数分类讨论的方法，学生会不会很容易想到.

当a>0时，令g（x）=f（x）-axcosx=x+sinx-axcosx，则g′（x）=1+cosx-a（cosx-xsinx）=1+（1-a）cosx+axsinx.

①当1-a≥0，即00，所以g（x）在上为单调增函数.所以g（x）≥g（0）=0+sin0-a·0·cos0=0，符合题意.所以0

②当1-a<0，即a>1时，令h（x）=g′（x）=1+（1-a）cosx+ axsinx，于是h′（x）=（2a-1）sinx+axcosx.

因为a>1，所以2a-1>0，从而h′（x）≥0.所以h（x）在上为单调增函数.所以h（0）≤h（x）≤h即 2-a≤h（x）≤a+1，所以2-a≤g（′x）≤a+1.

当2-a≥0，即1

综上所述，实数a的取值范围为（-∞，2］.

相信读者看完也会觉得这道题用分类讨论的方法确实太难想，可能学生还是比较容易想到分离参变量的方法，从阅卷情况看也是这样.接下来我们一起来瞧瞧为什么很多学生分参做不下去？

五、反思教学，方能提高

通过对上面几道所谓无法分离参变量的题目的分析后，笔者对教学有几点反思：

（1）解题教学时要学会倾听学声，了解学情，把握好学生的思维起点.课堂教学中教师要立足于讲清解题思路，要将解题的思维过程暴露给学生.不要就题论题，要多讲些如何想的，少讲些如何算的，要教会学生为什么这样解？解此类题的思路是什么？学生最关心的问题是什么？当初你是如何想到这样解的？今后再遇到类似的问题如何下手？要注意讲清思路受阻的原因，以及打开解题思路的步骤、方法.哪怕受阻是暂时的知识，内容不够，也要视情况补充.

（2）教师要认识到对于很多数学问题，教师与学生的认知往往不一样，不能把你认为的好方法直接灌输给学生，形成学生思路单一化，要遵循学生的认知规律，强化学生的“最爱”解法时，还要不失时机地引导学生从变化的角度看问题，带他们进入一个新境界，拓展学生思维，提升学生能力，升华学生本领.

（3）解题时要注意通性通法的讲解，也要注意一题多解，多个方法之间注意比较.就如本文提及的恒成立问题，分离参变量是好方法，但不是唯一的方法，还可以构造新函数，分类讨论.到底哪个方法好，不能一概而论.这就提醒我们平时教学中要具体问题具体分析.

（4）利用好网批试卷后的统计数据，可以促进教学有效性的提升，使教师的“教”、学生的“学”在数据的引领下提高效率，学生的解答就是学生的“声音”，倾听他们的“声音”，从而了解学生的学情，优化我们的教学效果.

六、结束语

“课堂是一门有遗憾的艺术”，但关键部分处理不好而出现的种种遗憾，有时恰恰是数学问题的核心、知识的重点、学生的盲点，因此我们要以学生为本，以学生的发展作为教学根本目的，能倾听学生的心声，及时反思，冷静分析，找出问题，并制定相应的对策；要有勇气，能够自我否定，及时弥补，这样方能取得成功！

1.杨晓翔.细节决定成败［J］.数学通报，2015（10）.

2.展国培.增强思辨意识发展思维能力［J］.数学通报，2015（9）.F