关于正规函数和球面导数乘积的进一步结果

戚建明，朱泰英

(上海电机学院 数理教学部，上海 201306)



关于正规函数和球面导数乘积的进一步结果

戚建明，朱泰英

(上海电机学院 数理教学部，上海 201306)

基于亚纯函数正规族理论，运用正规函数的概念和球面导数乘积的形式，获得了一些新的结果，改进了Xu和Qiu得到的相关结果.

亚纯函数； 正规族； Nevanlinna理论； 球面导数

如果函数f(z)除去极点之外在整个复平面上是解析的，我们称其为亚纯函数.我们假定读者熟悉Nevanlinna理论[1-2].当r→∞时，除去r的有限线性测度，记S(r,f)=o(T(r,f)).设f(z)和a(z)为复平面上的亚纯函数.如果T(r,a)=S(r,f)，则a(z)称为f(z)的小函数.设D为上一区域且F为D上的一族亚纯函数.F在区域D上正规，即如果每一序列{fn}⊂F有一子序列{fnj}在区域D上按球径一致收敛为一亚纯函数或者∞[1-2].并设Δ为复平面上的一单位圆.

正规函数的概念是由Lehto和Virtanen[3]引入的，且他们证明关于正规函数与球面导数的一特征：一函数f在Δ上正规当且仅当

这里

是f的球面导数.

1998年，Chen和Lappan[4]证明了如下结果.

定理A[4]设f为Δ上的一亚纯函数且f的所有零点重数至少是3.对任何的z∈Δ，如果存在正数δ和M满足

f#(z)(f′)#(z)(f″)#(z)≤M

(1)

且满足|f(z)|≤δ和(1-|z|2)|f′(z)|≤δ,则f是一正规函数.如果f所有的零点是重的且对任何的z∈Δ，且式(1)被

(1-|z|2)f#(z)(f′)#(z)≤M

或者

(f′)#(z)≤M

所取代且|f(z)|≤δ和(1-|z|2)|f′(z)|≤δ成立，则结论仍然成立.

2015年，Xu和Qiu[5]运用与Chen和Lappan[4]不同的方法并且获得如下结果.

定理B[5]设f为Δ上的一非常数的亚纯函数.假定存在M>0且对任何的z∈Δ，如果f(z)=0使得|f′(z)|≤M和|f″(z)|≤M成立.如果存在一含有12个不同点的集合E1在上，对任何的z∈Δ∩f(-1)(E1)且存在一正数K1使得

f#(z)(f′)#(z)(f″)#(z)≤K1

(2)

成立，则f是一正规函数.

定理C[5]设f为Δ上的一非常数的亚纯函数，假定存在M>0且对任何的z∈Δ,如果f(z)=0使得|f′(z)|≤M.如果

(i) 存在一含有8个不同点的集合E2在上，对每一个z∈Δ∩f(-1)(E2)且存在一正数K2满足

f#(z)(f′)#(z)≤K2

(3)

或者

(ii) 存在一含有6个不同点的集合E3在上，对每一个z∈Δ∩f(-1)(E3)且存在一正数K3满足

(f′)#(z)≤K3,

(4)

则f是一正规函数.

在本文中，我们获得如下结果.

定理1 设f为Δ上的一非常数的亚纯函数且k≥2为一正整数.假定存在M>0，对任何的z∈Δ，只要f(z)=0且满足|f(i)(z)|≤M(1≤i≤k+1).如果存在一含有2k+10不同个点的集合E1在上，对每一个z∈Δ∩f(-1)(E1)且存在一正数K1满足

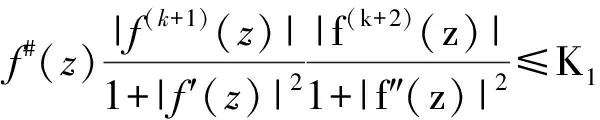
(5)

则f是一正规函数.

定理2 设f为Δ上的一非常数的亚纯函数且k为一正整数.假定存在M>0，对任何的z∈Δ，只要f(z)=0且满足|f(i)(z)|≤M(1≤i≤k).如果

(i) 存在一含有k+7个不同点的集合E2在上，对每一个z∈Δ∩f(-1)(E2)且存在一正数K2满足

(6)

或者

(ii) 存在一含有k+5(k≥2)个不同点的集合E3在上，对每一个z∈Δ∩f(-1)(E3)且存在一正数K3满足

(7)

则f是一正规函数.

注1 在式(5)，(6)，(7)中如果k=1，则分别是式(2)，(3)，(4)，且定理1，2就是定理A，B.因此在定理1和定理2的(ii)中我们考虑的是k≥2的情形.

为了证明我们的定理，需要下面3个引理：

引理1[1-2]设f为一在上非常数亚纯函数，且设a1,a2,…,aq(q≥3)∈∪{∞}为不同的复数，则

引理2[1-2]设f为一在上非常数亚纯函数，且设k∈，则

T(r,f(k))≤(k+1)T(r,f)+S(r,f).

下面的引理[4]是由Chen和Lappan引入的.

对于α=0的情形，由Lohwater和Pommerenke[6]所证.

下面我们来证明定理1，在证明中运用文献[5]中的一些思想.

假定f不是正规函数.则由引理3，存在一点列zn∈Δ，|zn|→1，和一正数序列ρn满足ρn→0且

gn(ζ)=f(zn+ρnζ)→g(ζ)

(8)

(9)

假定g(ζ0)=0.运用Hurwitz’s定理我们得到存在ζn,ζn→ζ0满足f(zn+ρnζn)=0.对足够大的n，由ρn→0即zn+ρnζn∈Δ.则由假设，我们有|f(i)(zn+ρnζn)|≤M(1≤i≤k+1).从式(9)可得，我们有

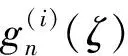
(n→∞).即得g(i)(ζ0)=0(1≤i≤k+1).则g的所有零点重数至少是k+2.即g是一非常数函数且对1≤i≤k+2,g(i)≢0.

设E1={a1,a2,…,a2k+10}，这里a1,a2,…,a2k+10为上不同的点.现在假定g(ζ0)=ai∈E1.由式(8)和Hurwitz’s定理，存在一点列ζn,ζn→ζ0满足f(zn+ρnζn)=ai.简之，设un=zn+ρnζn.显然对充分大的n有un∈Δ，且设un∈Δ∩f(-1)(E1).则由假设，对充分大的n有

因此，当n→∞时，有

(10)

即得到

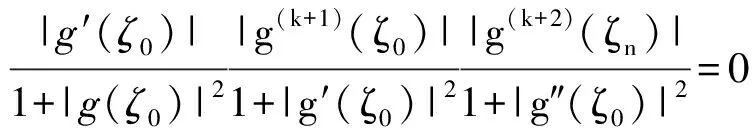
因此对每一个ai∈E1，g-ai的任一零点肯定是g′g(k+1)g(k+2)的零点.对1≤i≤k+2，记g(i)≢0，我们得到

联系引理1和引理2，得到

T(r,g′)+T(r,g(k+1))+T(r,g(k+2))+S(r,g)≤(2k+7)T(r,g)+S(r,g),

(11)

即T(r,g)≤S(r,g)，矛盾.定理1获正.

下面我们来证明定理2，在证明中运用文献[5]中的一些思想.

(i) 假定f不正规.则由引理3，存在点列zn∈Δ,|zn|→1，且一正数序列ρn满足ρn→0使得

gn(ζ)=f(zn+ρnζ)→g(ζ)

(12)

(13)

运用和定理1相同的证明方法，我们得到g的所有零点重数至少是k+1，即对1≤i≤k+1有g(i)≢0.

设E2={a1,a2,…,ak+7}，这里a1,a2,…,ak+7是中不同的零点.假定g(ζ0)=ai∈E2.运用式(12)和Hurwitz’s定理，则存在一点列ζn,ζn→ζ0使得f(zn+ρnζn)=ai.简之，设un=zn+ρnζn.显然，对充分大的n有un∈Δ，且un∈Δ∩f(-1)(E1).则由假设，对充分大的n有

因此，当n→∞，得到

(14)

即得到

因此对每一个ai∈E2，g-ai的任一零点肯定是g′g(k+1)的零点.即对1≤i≤k+1，g(i)≢0，我们得到

由定理1的证明，由引理1和引理2，我们得出T(r,g)≤S(r,g)，矛盾.(i)获证.

gn(ζ)=f(zn+ρnζ)→g(ζ)

(15)

类似于定理1的证明，对1≤i≤k+1，我们有g(i)≢0和式(9).

设E3={a1,a2,…,ak+5}，这里a1,a2,…,ak+5是上不同的点.现在假定g(ζ0)=ai∈E3.由式(15)和Hurwitz’s定理，这里存在一点列ζn,ζn→ζ0使得f(zn+ρnζn)=ai.简之，设un=zn+ρnζn.显然，对充分大的n有un∈Δ，且设un∈Δ∩f(-1)(E1).则由假设对充分大的n有

因此

(16)

(n→∞)，即得

对每一个ai∈E3,g-ai的任一零点肯定是g(k+1)的零点.对1≤i≤k+1，有g(i)≢0，我们得到

再次运用引理1和引理2，我们得到一矛盾.定理2获证.

[1] YANG L. Value distribution theory [M]. Berlin：Springer, 1993.

[2] HAYMAN W K. Meromorphic functions [M]. Oxford：Clarendon Press, 1964.

[3] LEHTO O, VIRTANEN I. Boundary behaviour and normal meromorphic functions [J].ActaMathematica,1957,97(1)：47-65.

[4] CHEN H, LAPPAN P. Products of spherical derivatives and normal functions [J].JournaloftheAus-tralianMathematicalSociety, 1998,64(2)：231-246.

[5] XU Y, QIU H L. Normal functions and products of spherical derivatives [J].AnalysisandMathematicalPhysics, 2015,5(3)：241-248.

[6] LOHWATER A J, POMMERENKE C. On normal meromorphic functions [J].AnnalesAcademiaeScientiarumFennicaeMathematica, 1973,550：1-12.

Further Results about Normal Functions and Products of Spherical Derivatives

QI Jianming, ZHU Taiying

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

Based on the theory of normal families of the meromorphic functions, some new results are obtained by using the concept of normal function and the product of spherical derivative, also Xu and Qiu’s results are improved.

meromorphic function; normal family; Nevanlinna theory; spherical derivative

0427-7104(2016)05-0565-05

2016-01-11

国家自然科学基金数学天元青年基金(11326083)；上海市教委科研创新项目(14YZ164)；上海电机学院重点学科(13XKJC01)；上海电机学院学科建设项目(16JCXK02)

戚建明(1981—)，男，博士，副教授，E-mail：qijianmingsdju@163.com.

O 174.5

A