谈变式教学在初中数学习题中的运用

浙江省桐乡市洲泉中学 钱子荣

谈变式教学在初中数学习题中的运用

浙江省桐乡市洲泉中学 钱子荣

提高课堂效率，减轻学生的课业负担，是每一个一线教师的迫切追求；发展思维品质，培养学生探索、创造、创新能力，追求有效地数学课堂教学是新课标要求的重要体现；而变式教学有利于培养学生发现问题、探究问题和解决问题的能力，是思维训练以及能力培养的重要途径，为此，在当今全面实施新课程、深化教育改革的新时期，重新审视数学变式教学，阐明其原理、方法等精神实质，具有重要而深远的现实意义.

变式 变式教学 习题

变式是创新的重要途径，是模仿与创新的中介，是一种重要的思想方法.通过变式进行教学，展示知识的发生、发展和形成的完整认知过程，有利于培养学生发现问题、探究问题和解决问题的能力，是思维训练以及能力培养的重要途径.

例题、习题教学是把知识、技能和方法联系起来的主要纽带，是数学教学的重要组成部分.当学生掌握问题的基本解法后，教师可引导他们对问题进行多角度、多层次的思考，通过变式提出新问题或获得同一问题的多种结果.

例题、习题变式包括一题多解(证)、一题多变、多题一解(一法多用)等.

一、一题多解(证)

一题多解(证)变式就是对同一个数学问题，启发学生探索不同的解题方法，培养学生的发散思维和创新意识.

例一个六边形如图1，已知AB∥DE，BC∥EF，CD∥AF，求∠A+∠C+∠E的度数.

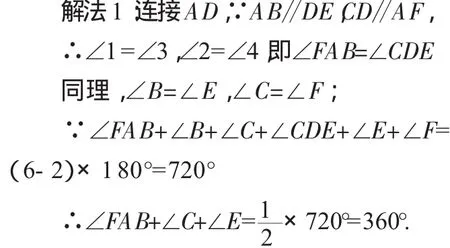
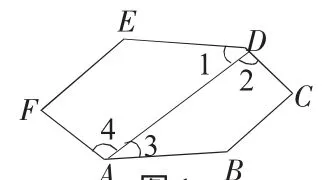
图1

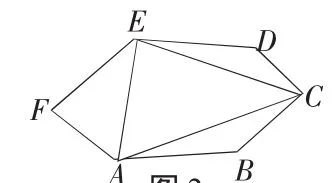
图2

解法2：连接AC、AE、CE，如图2，

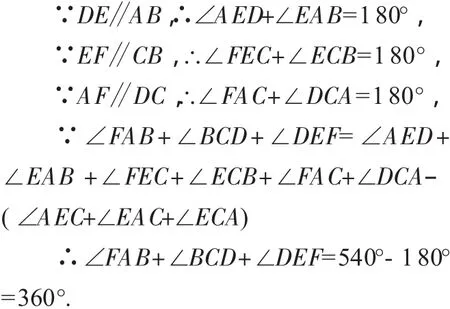
解法3：向两个方向分别延长AB，CD，EF三条边，构成△PQR，如图3，

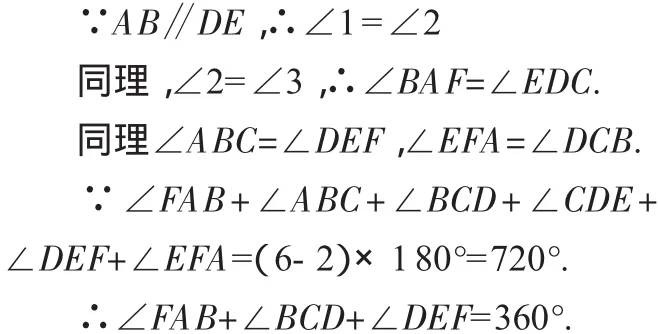
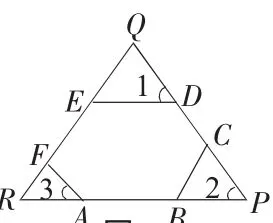
图3

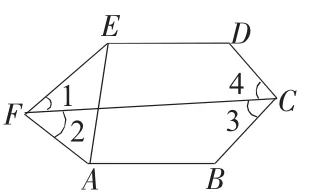
图4

解法4：连接AE、FC，如图4，

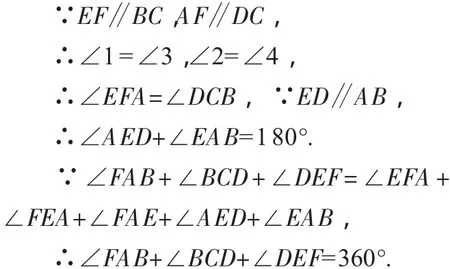
解法5：延长AB、DC交于点P，连接EB，如图5，

同上证法可得：

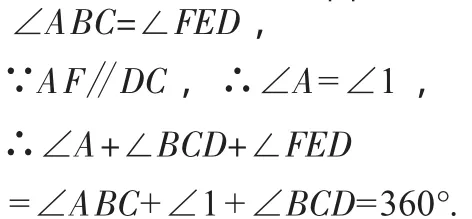
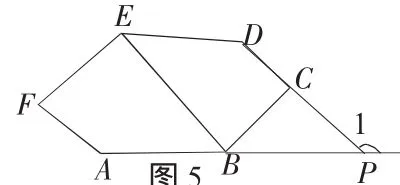
图5

一题多解变式需要丰富的知识经验.对于同一个问题通过多种方法来证明（求解），不但熟知数学知识的应用，而且增强了学生思维的灵活性、深刻性、广阔性、变通性；通过几种方法的比较，感受到数学的简洁美、和谐美，只有这样的审美感受，才能真正激发学生的学习兴趣；让学生认识到：已掌握的通法并不是惟一的解题方法，还可以根据题目的特点，改变考虑问题的角度，去寻找更简捷、巧妙的方法；在平时的学习或复习中，应广开思路、发散思维、探求问题的多种解法，从而使四基得到训练、能力得到增强、智力得到开发；多种方法的灵活运用能让学生产生“海阔凭鱼跃，天高任鸟飞”的感觉.

二、一题多变

一题多变，就是对某个题目进行多角度、多层次的条件、结论的变换，使一个题变为一类相似题，达到融会贯通的目的.一题多变有利于培养学生的创新能力，形成良好的思维品质.一题多变主要有条件变式、逆向变式、结论变式、拓广变式等.

1.条件变式.

所谓条件变式，就是引导学生对某一题目的条件适当变化，得到一组变式题，通过对这组变式题的分析、解决，让学生掌握某类问题的题型结构，深入认识问题的本质，提高解题能力.

例已知：如图1，在正方形ABCD中，E、F分别是BC，CD上的点，AE⊥BF.求证：AE=BF.

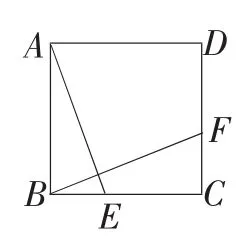
图1

图2

本题证明并不难，在学生证好本题之后，尝试将该题作如下变化：

变式1：如图2，四边形ABCD是正方形，E、F分别是BC，CD延长线上的点，AE⊥BF.求证：AE=BF.

变式2：如图3，四边形ABCD是正方形，E、F分别是CB，DC延长线上的点，AE⊥BF.求证：AE=BF.

变式3：将图1中的线段BF向上平移，如图4，其余条件不变.求证：AE=HK

图3

变式4：将图4中的线段AE向左平

移，如图5，其余条件不变．求证：EF=HK.

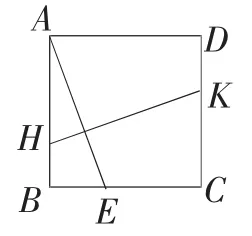
图4

图5

作如上变式设问后，创设了学生活动的情境，在动中提高学生举一反三、触类旁通的能力，这不仅加深学生对知识的深层次理解，更对培养学生思维的发散性和创造性有着重要作用.

2.结论变式.

所谓结论变式，就是抓住一个问题的条件，引导学生运用类比，联想等发散思维，将问题的结论向横向、纵向拓展，以达到以点串线、举一反三、触类旁通的目的.

例：（2011·遵义）已知抛物线y=ax2+bx+3（a≠0）经过A（3，0），B（4，1）两点，且与y轴交于点C．

（1）求抛物线y=ax2+bx+3（a≠0）的函数关系式及点C的坐标；

（2）如图1，连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；

图1

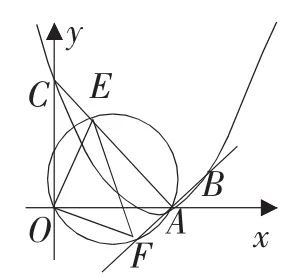
图2

（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标．

变式1：点P为抛物线对称轴上的一个动点，其中△APB的周长最短，求点P的坐标；

变式3：在抛物线上找一点P，使△APB是以AB为底边的等腰三角形，求点P的坐标；

变式4：连接AC，在直线AC下方的抛物线上找一点P，使S△APC最小，求点P的坐标；

变式5：在平面直角坐标系内找一个点P，使得以A、B、C、P为顶点的四边形为平行四边形，求点P的坐标；

一题多变其实就是结论开放型的习题，教学时应经常启发学生多角度地引申问题，培养学生的创造意识与探索精神.

3.逆向变式.

所谓逆向变式，就是当一个命题得到解决以后，启发学生探求这个命题的逆命题是否成立，有利于培养学生的逆向思维，提高学生的创造能力.

例1如图，正方形ABCD中，点E、 F分别在BC、CD上，且∠EAF=45°，求证：BE+DF=EF.

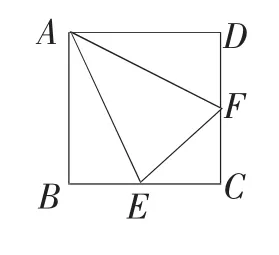
变式：原题其他内容不变，把结论“BE+DF=EF”变为条件，把条件“∠EAF= 45°”变为结论，则结论成立吗？

例2角平分线上的点到这个角两边的距离相等.

变式1：“到一个角两边距离相等的点在这个角的角平分线上”，是真命题吗？

变式2：“在一个角的内部，到这个角两边距离相等的点在这个角的角平分线上”，是真命题吗？

因为命题的逆命题与原命题的真假性不一定相同，从思维训练的角度出发，逆向变式有助于培养学生的逆向思维，有助于学生对数学问题的理解和掌握.

三、一法多用（多题一解）

数学中有许多不同的分支，常常出现内容上的相互渗透.不同单元的问题虽然形式不同，但这些题目本质不变，所以方法与结果相同.另外，选择题、填空题、解答题、证明题等不同题型之间的转换，也可列入一法多用（多题一解）的范围.

1.等价变式.

所谓等价变式，就是通过互为逆否命题的转换、不同单元内容的表述等手段得到与原命题等价的变式题组，达到多题一解、强化方法的目的.

例下列问题虽然位于不同的知识单元，但都使用同一种方法，即利用一元二次判别式来解题：

变式1：m为何值时，x2-（m-3）x+8= 0无实根？

变式2：m为何值时，f（x）=x2-（m-3）x+8的图像与x轴无交点？

变式3：m为何值时，x2-（m-3）x+8≤0的解集是空集？

变式4：m为何值时，x2-（m-3）x+8不能分解为两个一次因式的积？

变式5：m为何值时，抛物线y=x2+8与直线y=（m-3）x无交点？

上述五个问题其实是等价的，其解题方法相同.通过上面的等价变式，使学生明确含参变量的二次方程、二次函数、二次不等式、二次三项式及二次曲线交点问题之间的内在联系及相互转化的规律，开阔知识视野和解题思路.

2.题型变式.

所谓“题型”，指的是题目的结构形式，也就是在一道题目中，将已知与未知及解题指令中的所有事项相互联结起来的逻辑形式.同一数学问题，可以有用不同的表现形式，如填空题、选择题、判断题、计算题、证明题等.同一问题在不同题型之间的转换就是题型变式.

变式3：计算：sin150.

题型变式有助于学生透彻理解题目的本质属性，开阔解题思路，提高解题能力.

常言道，要给学生一杯水，教师就要有一桶水.这就要求我们不断提高自己的专业素养和教学水平.当然，教学方式不能仅局限于变式教学，而要灵活运用各种教法学法，提高学生的数学素养.

[1]史宁中主编.义务教育数学课程标准解读（2011版）[M].北京：北京师范大学出版社.2012：6

[2]卜启虎.反思——高效学习方法[J].中国数学教育（初中版）.2011（4）：17

[3]朱信化、王锋.变式中感悟习题魅力探究中提升创新能力[J].中国数学教育（初中版）.2012（7/8）：50