例谈初中数学题中隐含条件的挖掘

浙江省桐乡市洲泉中学　俞梅芳

例谈初中数学题中隐含条件的挖掘

浙江省桐乡市洲泉中学俞梅芳

初中数学题目有很多看起来平淡无奇的常规题，这些平淡的背后隐藏着命题者精心设计的一个个小“陷阱”，他们把一些已知条件隐藏在题目中，未明确表达出来，而这些隐含的条件，往往是解题的关键，这些条件容易被忽视，或隐藏很深，不易被挖掘，往往使求解陷入困境，给人“山重水复疑无路”的感觉.若能深入挖掘题中的隐含条件，并充分加以利用，往往可以使问题得到迅速而巧妙的解决.

初中数学隐含条件挖掘

要想正确求解初中数学题目，审题是解题的第一步，审题时要多角度、无遗漏地收集题目中的信息，挖掘题目中隐含的条件，化隐为显，这就需要有扎实的基础知识，熟练的基本技能，严谨的思维能力和灵活的思想方法，通过观察、分析逐步探索和转化.如果粗心大意，急于求成，只看见事物的现象，而看不见事物的本质，往往使解题偏离方向，而走错了道路.

隐含条件存在的形式多种多样，有的以文字形式存在，也有的存在于图形中，下面就结合数学实践对隐含条件的发现和运用进行浅显的探讨.

一、从数学概念中挖掘隐含条件

数学概念题，简单地说，就是根据数学概念、性质等内容所设置的问题案例.初中生在数学概念题的解答中，需要对数学概念的整体进行正确的理解和掌握，才能把握住数学概念的实质，而部分初中生由于对数学概念、性质等内容，特别是重点字词的内涵，不能有效理解和掌握，导致解题时出现审题不清、理解错误.例如：同类项、负整数幂、零指数幂、二次根式、分式、一元二次方程等概念.

例1：已知5a2bn-2与-2am-1b3的和是一个单项式，求m、n的值.

分析与解：只有同类项才可以合并，因此：m-1=2，n-2=3，

∴m=3，n=5.

例2：求使下列式子有意义的x的取值范围.

（1）（x+2）-3（2）（x-1）0

分析与解：（1）隐含条件：必须底数不为零，即：x+2≠0，∴x≠-2；

（2）隐含条件：必须底数不为零，即：x-1≠0，∴x≠1；

（3）隐含条件：必须被开方数为非负数，即：x+6≥0，∴x≥-6.

（4）隐含条件：必须分母不等于零，即：x-3≠0，∴x≠3.

二、从数学公式中挖掘隐含条件

许多数学知识是通过数学公式来呈现的，学生对数学公式的理解程度决定了其对数学知识的达成度.

例3：已知关于x的一元二次方程（m2-1）x2-（2m+1）x+1=0有两个不相等的实数根，求m的取值范围.

分析与解：因为一元二次方程有两个不相等的实数根，根据根的判别式b2-4ac＞0得而判别式有前提条件的，隐含了二次项系数不为零，则m2-1≠0，所以m≠±1，即且 m≠±1.

三、从结构特征中挖掘隐含的条件

很多数学题会给各种条件，有些是有用信息可以帮助解题，有些是无用信息用来混淆解题思路，所以学生需要在这种罗列的结构信息中，进行抽丝剥茧的分析来得到被隐含的条件.

例4：已知（a2+b2）2-3（a2+b2）-10=0，求a2+b2的值.

分析与解：用整体思想把a2+b2看成一个整体，并用因式分解法得（a2+b2+2）（a2+b2-5）=0，则a2+b2=-2，或a2+b2=5，而条件中隐含了a2+b2≥0，所以a2+b2=5.

四、从图形中挖掘隐含的条件

几何图形是由许多基本元素和基本图形构成的，而有些几何问题，已知中给出的条件往往对这道题不够进行解答，似乎缺少了条件，而这正是题目中隐含的条件，所以在解题时要对图形进行观察和有分析地进行思考，从而把握图形的基本特征，找到解决问题的突破口.

例5：在Rt△ABC中，∠BAC=90°，AB=AC=2，以AC为一边，在△ABC的外部作等腰直角三角形ACD，则线段BD的长为__________.

分析与解：要想解决本题，首先要找到线段BD，由于等腰直角三角形ACD的位置具有不确定性，因此要充分挖掘图形中隐含的条件，通过分类解决此题；

解：①以A为直角顶点，向外作等腰直角三角形DAC，

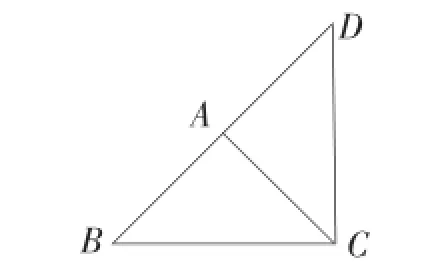
∵∠DAC=90°，且AD=AC，

∴BD=BA+AD=2+2=4；

②以C为直角顶点，向外作等腰直角三角形ACD，

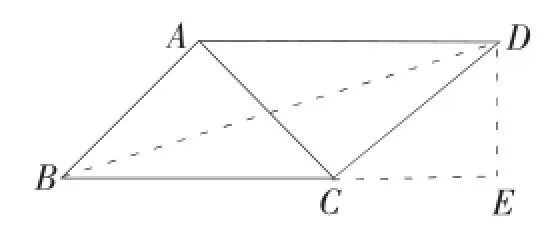
连接BD，过点D作DE⊥BC，交BC的延长线于E.

∵△ABC是等腰直角三角形，∠ACD=90°，∴∠DCE=45°，

又∵DE⊥CE，∴∠DEC=90°，

∴∠CDE=45°，

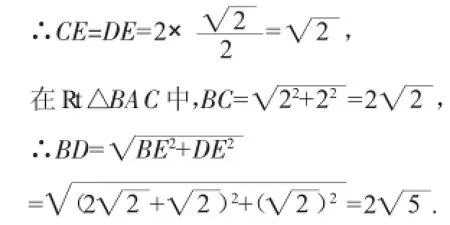
③以AC为斜边，向外作等腰直角三角形ADC，

∵∠ADC=90°，AD=DC，且AC=2，

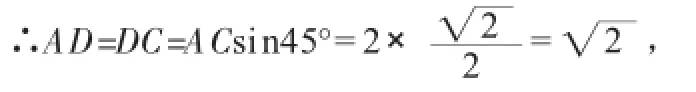
又∵△ABC、△ADC是等腰直角三角形，

∴∠ACB=∠ACD=45°，∴∠BCD=90°，又∵在Rt△ABC中，

五、从图像中挖掘隐含的条件

图像是表示函数的一种重要形式，函数图像最能够形象地反映数字的规律的变化，它将函数的各种性质及特点无保留地展现在你的面前，正因如此，函数图像也具有较强的解题功能，很多看似复杂的问题，通过绘制函数图像，能得到初步的感知，或者利用图像上的信息，并根据函数的相关知识解决问题.

例6：如图：已知抛物线y= ax2-3x+a2-1的图像，则求a的值.

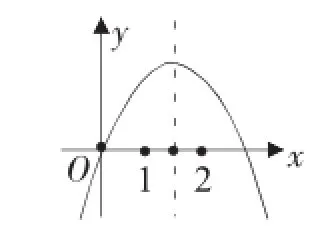
分析与解：由抛物线的性质可知，图像中隐含两个条件，即a＜0，且抛物线经过原点，得：a2-1=0且a＜0，所以a=-1.

六、从问题的实际意义中挖掘隐含的条件

数学来源于生活，同时又服务于生活.对于实际问题，在求解后要检验结果的合理性，是否符合实际，因此要挖掘出这些隐含的条件，才能正确求解.

例7：某公司在甲乙两地销售一种品牌车，利润（单位：万元）分别为：L1=5.06x-0.15x2，L2=2x，其中x为销售量（单位：辆），若该公司在两地共销售15辆车，求其最大利润.

分析与解：学生解此题时，常由于忽略变量x的实际意义，而得到错误答案45.606（万元）.考虑到变量x的实际意义，正确解答如下.

解析：设甲地销量为x辆，则乙地销量为（15-x）辆，该公司销售利润为

y=5.06x-0.15x2+2（15-x）

=-0.15x2+3.06x+30

=-0.15（x-10.2）2+45.606

∵x∈N，

∴当x=10时，ymax=45.6

即该公司销售汽车所获得的最大利润为45.6万元.

综上，隐含条件的挖掘是初中生必备的解题技能，而隐含条件虽然会给我们的数学解题带来困扰和阻碍，但是，我们只要把多种方法结合起来使用，认真审题，从多角度、多方位、多层次去挖掘每个隐含的条件，并能有效地加以利用，就能发挥积极的作用，达到“柳暗花明又一村”的畅快，顺利到达解题的彼岸，从而真正提高自己解决问题和分析问题的能力.

［1］巧妙利用隐含条件解题.考试周刊.2013

［2］初中数学解题过程中隐含条件的解读.论文网.2015

［3］教学与研究.考试周刊.2013

［4］深挖题设条件中的隐含条件.中学数学研究.2012