Wi-Fi设备间节能通信抗频偏数据分组检测

杨帆，梁溪，龙柯宇，蒋李

（1. 电子科技大学通信与信息工程学院，四川 成都 611731；2. 中国民用航空局第二研究所，四川 成都 610041）

Wi-Fi设备间节能通信抗频偏数据分组检测

杨帆1，梁溪1，龙柯宇2，蒋李2

（1. 电子科技大学通信与信息工程学院，四川 成都 611731；2. 中国民用航空局第二研究所，四川 成都 610041）

提出了一种基于Wi-Fi接口的数据分组检测算法，它在OFDM符号同步定时度量函数中采用一种新型归一化因子作为分母，与传统方法相比，该算法不仅有较高的检测概率，而且阈值的设置无需预先估计频偏。理论分析和仿真结果表明，在AWGN信道中，提出的算法使数据分组检测阈值设置更为灵活。此外，在多径Rayleigh衰落信道下，阈值可以直接根据相应AWGN信道的情形进行设置。

绿色通信；D2D；OFDM同步；Wi-Fi；移动无线网络

1 引言

基于Wi-Fi的设备间 (D2D, device to device)通信是指Wi-Fi终端设备无需基础设施（如基站和接入点）节点的介入而直接通信的一种技术[1～3]。这些搭载Wi-Fi的终端设备采用802.11标准进行互联，实现数据传输或共享应用等任务。D2D通信按带宽可分为带内D2D和带外D2D，前者指在授权频谱范围内传输数据，而后者指采用其他无线通信技术在未授权频段进行的通信。带外 D2D通信由于具有较高的频谱效率、低能耗及时延小的特点，受到人们的广泛关注[4～6]。

D2D通信按控制分为受控和自组织2种方式，受控方式指完全由基站控制 D2D连接，而自组织方式指D2D设备自主地完成D2D连接的建立与维持，具有突发通信的特点。此外，现有的设备间通信大多采用自适应传输和反馈重传机制，而在自组织 D2D系统传输时，信号会因路径损失、阴影效应以及多径衰落的影响而发生畸变，使接收信号的信噪比起伏变化，导致同步系统数据分组检测的阈值难以确定。

正交频分复用(OFDM, orthogonal frequency di-vision multiplexing)是基于Wi-Fi无线传输协议的核心技术之一。实现OFDM可靠接收需要建立在高效的数据分组检测基础上。数据分组检测算法的优劣可以用漏检概率(MDP, missed detection probability)和误检概率(FAP, false alarm probability)来表征。MDP与FAP是阈值的函数，当阈值设置过大时，会造成信号MDP增大，增加分组丢失率；而阈值设置过小则使FAP增大，导致将超过阈值的噪声信号当作有效信号来处理，造成接收机功率的浪费。在 D2D突发通信中，接收端通过前导序列对突发信号进行检测，突发数据传输中的同步与相应的连续通信中的同步相比，对精确度和实时性有更高的要求。针对不同信道质量，可以用信噪比（SNR）来衡量，为实现高效同步，需要有较大的阈值设置范围，即对于某一给定的通信指标（如给定的FAP和MDP），应使FAP和MDP对应的阈值间隔尽可能得大。

对于符号同步技术以及数据分组检测，早在1997年，Schmidl和 Cox就提出了一种经典的OFDM时频联合同步算法，简称SC算法[7]。类似于SC算法，文献[8, 9]利用多块重复训练序列的自相关性，使基于 OFDM 的数据分组检测在独立Rayleigh多径衰落信道下同步性能良好。近年来，文献[10]进一步探讨了数据分组检测的阈值设置问题，并得到了定时度量的2个归一化因子，产生了差值的幅度(MoD, magnitude-of-difference)和幅度的差值(DoM, difference-of-magnitude)算法。MoD算法具有优异的检测性能，但与载波频偏(CFO, carrier frequency offset)相关，当CFO为零时，MoD算法性能最优。而DoM算法独立于CFO，但其检测性能与前者相比，性能欠佳，DoM算法仅略优于SC算法。

针对以上问题，本文着眼于自组织 D2D通信突发传输系统，研究基于Wi-Fi的数据分组检测问题，实现良好的节能通信。首先，文章介绍自相关特性的定时度量，基于自相关的OFDM短训练符号可用做同步和阈值的检测。接着，根据定时度量函数中的分子对同步头相邻的2个子块进行自相关的结果，提出一种新型的归一化因子作为定时度量函数的分母，它利用了传统的能量归一化因子与分子的自相关结果进行差分处理。该方法的优点在于可抑制较大的频偏，且独立于CFO。此外，在同步性能方面可以逼近最优MoD算法，并使在信道SNR波动较大时仍能够实现稳定高效的数据分组检测，从而尽可能避免不必要的后处理和反馈重传。

图1含D2D簇的移动网络模型和信号传输

2 系统模型

不失一般性，本文考虑任意2个D2D无线通信节点，并称这一对节点为D2D簇，如图1所示。在 D2D无线通信传输中，会经历不同程度的干扰和失真，包括路径损失、阴影效应、多径衰落和带外散射。因建筑物的阻挡和距离的变化，信道质量会随之变化，导致接收端SNR的波动较大，如图1中5～15 dB的波动，本文的目的是实现在SNR大范围波动的条件下，仍然能够灵活地设置阈值，并实现较为稳定和高效的数据分组检测。

首先考虑搭载Wi-Fi模块的D2D发送节点，采用如图2所示的OFDM同步头[11]。在该突发模式传输下，数据帧由同步头、信令和数据流组成，最开始为同步头，用于数据分组检测以及符号同步等操作，同步头之后是信令和数据流。

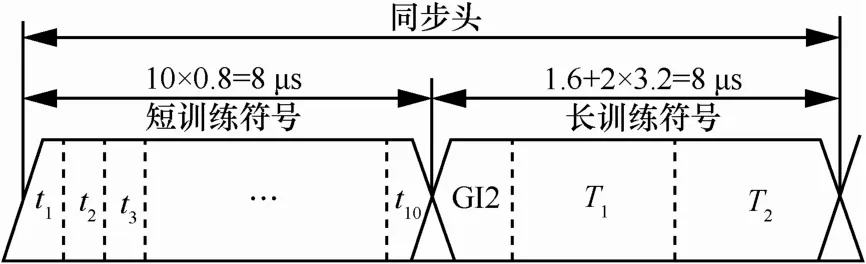
图2文献[11]中所采用的同步头结构

如图2所示，同步头可分为2个OFDM符号。第一个OFDM符号为短训练符号，它的每一个子块包括16个样点，持续0.8 µs。第二个OFDM符号包含 2个长训练符号和 1个保护间隔（GI, guard interval）。每个长训练符号包括 64个样点，持续3.2 µs，而保护间隔的样点数为32。信令域和数据域采用 64点快速傅里叶反变换(IFFT, inverse fast Fourier transform)，且每个OFDM符号的信令或数据域之前都有长度为K的循环前缀或保护间隔。由于短训练符号主要用于进行数据分组检测，也是本文重点考虑的对象，为便于后续讨论，采用训练符号替代短训练符号，特此说明。

对于D2D簇中的接收节点，在n时刻的接收信号的样值可表示为

其中，x( n)表示发送信号样值，h( l)表示第l条路径的信道脉冲响应，τm表示多径信道采样点的最大延迟。

假设接收到的训练符号和其他 OFDM 数据符号都是相互独立的，且服从均值为0，方差为的高斯分布。由文献[7, 8, 10, 12]可知，基于自相关特性的定时度量可统一表示为

其中，d表示在自相关窗[d−2K+1,d ]范围内最后一个样点时刻，此范围长度为2K，指对变量的模值运算，ΛΞ(d)是归一化因子，它是基于自相关定时度量函数分母的统一记号，上标Ξ表示算法名称代号，如SC、Minn、MoD、DoM或本文后续提出的新型归一化因子Pro。ϒ(d)可进一步表示为

其中，(·)H表示对变量的复合共轭运算，ΓΞ(d)中的分子为自相关部分。

不失一般性，可用d=0作为帧头和噪声的分界点，从而可以将时间轴划分为3个不同的区域。当da=(−∞,−1]时，表示只存在噪声的区域，当dp={[0,2K−2]∪[JK,(J+2)K−1]}时，表示含有部分同步头、部分有效数据以及噪声的区域；当df=[2K−1,JK −1]时，表示只含有同步头和噪声，而不包括有效数据的区域。

接下来，简要介绍文献[7, 8, 10]中的SC、Minn、MoD以及 DOM 算法中涉及的归一化因子ΛSC、ΛMinn、ΛMoD和ΛDoM，下文用来近似表示期望值E[z( n)]。

在文献[7]中，df和da范围内的归一化因子ΛSC可由式(5)给出。

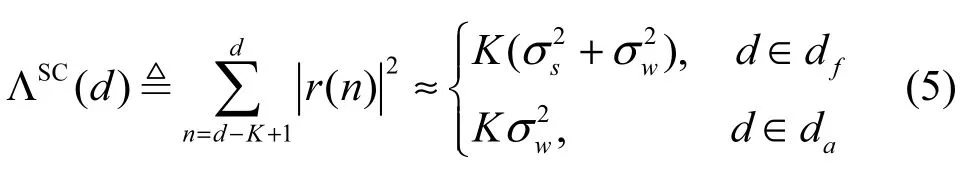
文献[8]中所提出的算法，在df和da范围内的归一化因子ΛMinn可表示为

而文献[10]算法中的归一化因子ΛMoD和ΛDoM分别定义为

和

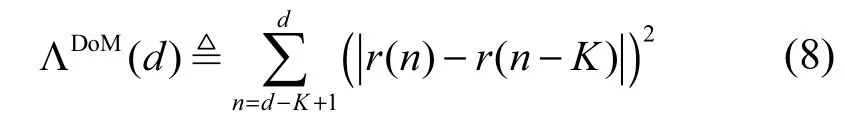
其中，如果d∈df，则，如果d∈da，则

3 本文提出的归一化因子

在附录中，分别讨论在da、dp和df这3个区域内的理论值。因为瑞利分布是莱斯分布的一种特殊情况，可在定义域上一致看成服从莱斯分布，其均值可近似为

其中，Lq(·)中在附录中的式(18)已有定义。时域上对应的2个参数v和2σ2总结如下

受文献[10]的启发，收到训练序列时，定时度量主瓣的锐化可通过对式(3)中的分子和分母部分做差分处理，因为两者在同步头到达区域，数值呈相反的变化趋势。最直接的考虑是通过利用ΛMinn(d)和做减法来设计一个新型的归一化因子，表示为

相应的定时度量采用的算法称为Pro算法。结合式(4)和式(6)，可得到所有d取值时，ΛPro(d)≥0，且有

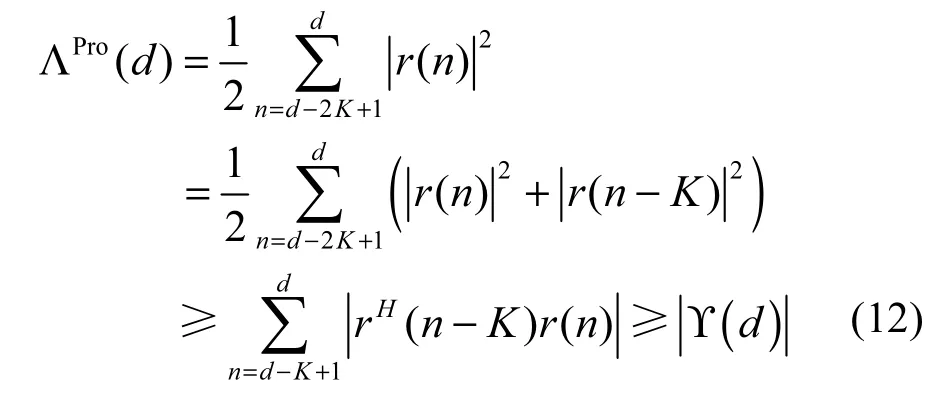
从节能 D2D通信的角度出发，定时度量函数中的分子和分母部分经过初始化运算之后，可通过类似自相关滑动窗的方法进行少量迭代运算来降低ΛMinn(d)和的计算量[8]。

下文通过仿真验证归一化因子ΛPro(d)的理论解析结果。在图 3(b)中看到，时间段的[16,159]区间内，ΛPro(d)曲线呈凹槽状，相应地，在图 3(a)中存在一个峰值。这个性质使所提出的算法能够使定时度量函数更加尖锐，为了更好地选择阈值，同时还保证在较大 CFO情况下检测算法的顽健性。在图3(b)中时间段[160,319]对应的不匹配区域是由图3(a)中的凹槽引起的。

正如文献[10]所述，ΓΞ(df)和ΓΞ(da)之间定时度量的差异对数据分组检测性能有显著影响，已经分别得出归一化因子ΛSC、ΛMinn、ΛMoD、ΛDoM、ΛPro以及自相关部分中的解析式。定时度量的定量分析可根据文献[10]中描述的方法进行计算和比较，具体的分析过程在此不再赘述。

图4所示为SNR=10 dB、ε=0及K=16时，在AWGN信道下，自相关部分和4种算法中归一化因子进行1000次仿真分别取均值得到的结果。从图中可看到，ΛSC(d)和ΛMinn(d)在[K−1,2K−2]范围内增加，达到峰值。然而，ΛMoD(d)、ΛDoM(d)和ΛPro(d)在此范围内下降至最小值，与相比，它们在该区域具有相反的变化趋势，需要特别指出的是此处ΛMoD(d)的性能是 CFO为零的条件下得出的。

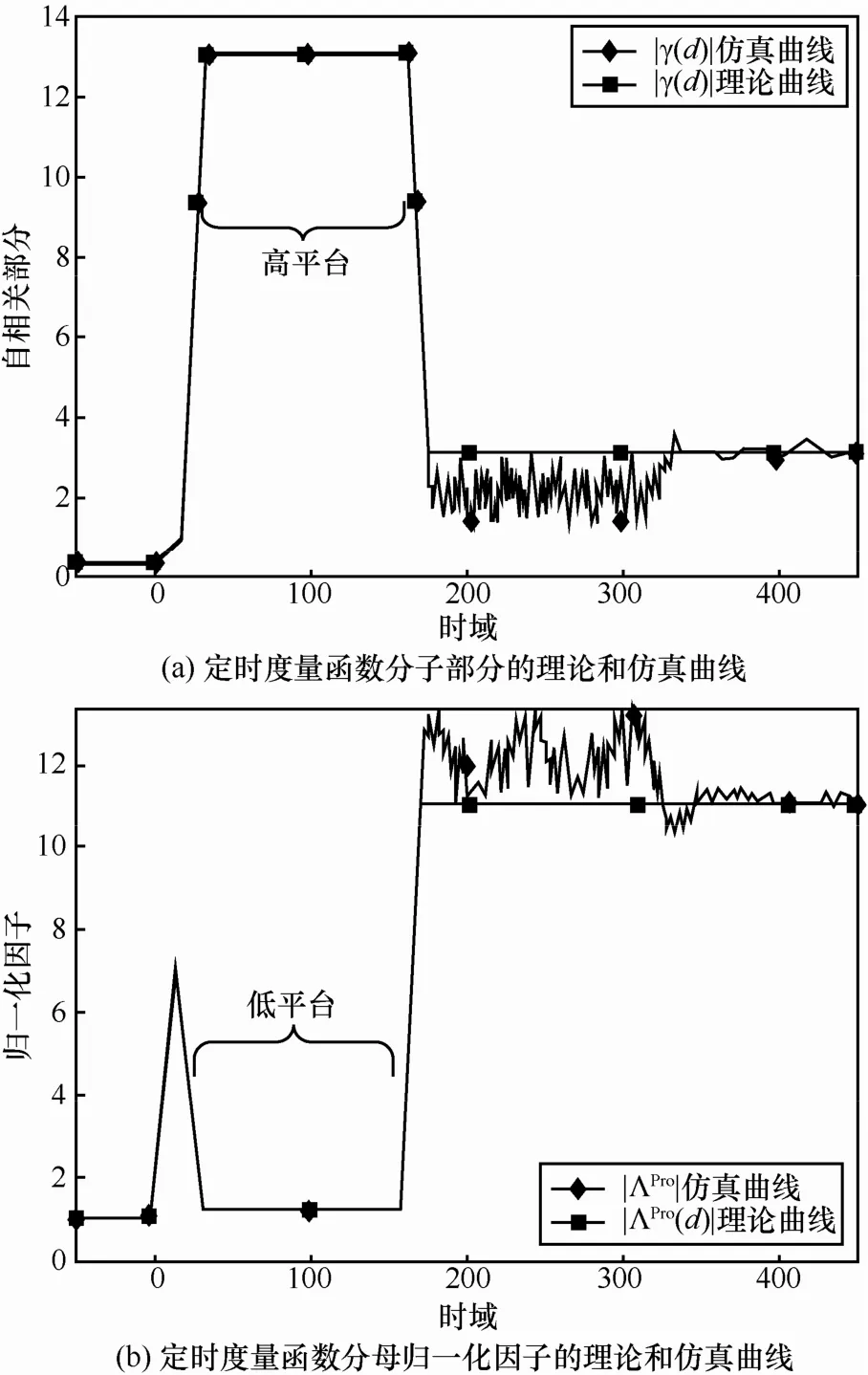
图3定时度量函数分子、分母（归一化因子）各自的理论和蒙特卡洛仿真曲线对比

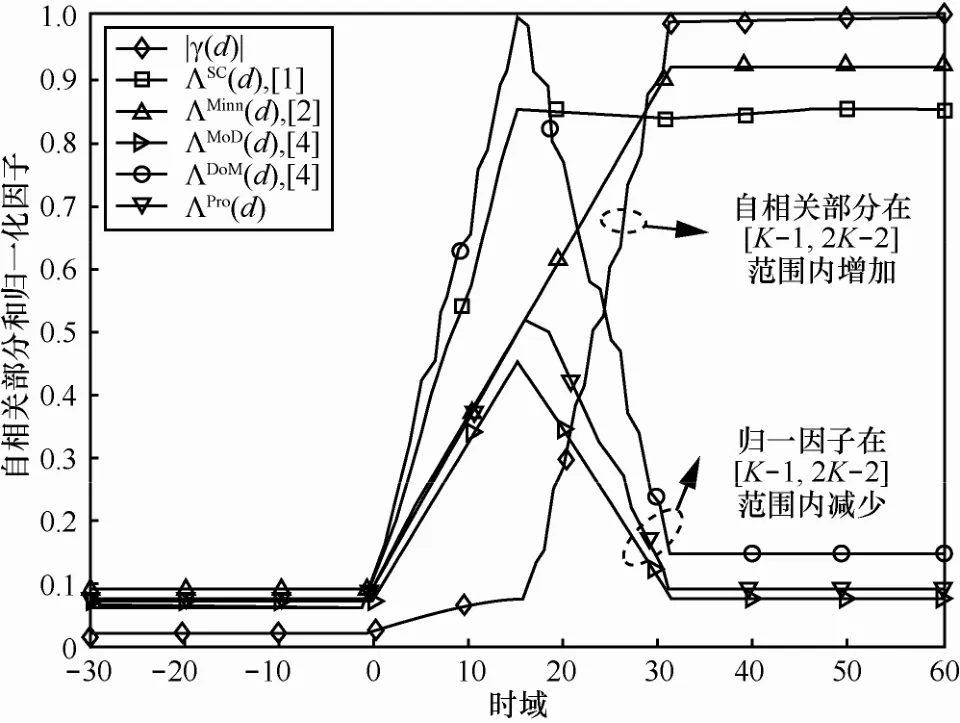
图44种算法中归一化因子的曲线

4 性能评估

前面提到，数据分组检测算法可由2种类型的概率来表征，即FAP和MDP。FAP是指在没有信号的情况下，噪声的时间度量Γ(d)大于系统同步误检阈值Fη的概率，用FP表示；MDP是指在信号已经到达的情况下，同步头时间度量Γ(d)小于系统漏检阈值ηM的概率，用PM表示，即

这里，H1和H2分别对应完全是噪声的区域(d∈da)和完全是同步头出现的区域(d∈df)。节能 D2D通信中阈值设定的目标是为了较方便地设置阈值η的值，以同时兼顾误检和漏检概率的要求。因此，阈值η的选取需满足ηF≤η≤ηM，在给定某一SNR的条件下，阈值比率的值越大，阈值越容易设置。本文对每一个给定SNR值进行了超过2× 105次的模拟，用以实现阈值的设置。由上述可知，在概率误差允许范围内，当PF=PM时，比率ρ的值越大，说明阈值的选择越灵活。此处，定义一个交叉点概率PC，当ηF=ηM（或ρ=1）时， PC=PF=PM。PC对应于阈值η可以看作是最优阈值，它保证了FAP与MDP同时达到最低。

图5曲线所描绘的情形是在AWGN信道下，当SNR=10 dB 、ε=0.01以及K=16时，文中提到的4种算法的FAP和MDP曲线性能。对于SC算法，2个误差概率都可最小化至PC=10−3，对应于η≈0.75。对于MoD和DoM算法，从CFO和MoD因子的关系知道，当CFO较大时，MoD因子性能会显著恶化。此时，MoD因子与DoM因子有着近乎相同的性能。与其他3个算法相比，Minn算法和Pro算法有着近似的交叉点概率PC。然而，因Minn算法中FAP和MDP曲线之间的间距较窄，故其阈值的选择较为有限。相反，Pro算法在FAP和MDP曲线之间提供了一个较宽的间隙，在设定阈值时能保持两者之间的平衡，更具有灵活性。

需要说明的是，对于以上几种算法，为获得更低的交叉点概率PC，可以通过增加自相关窗的长度，来获得更好的数据分组检测性能，但需要在定时度量函数初始化时增加一定的运算量，在后续迭代处理过程中的运算量几乎不变。如第一种方式：短训练符号包含了 10个相同的部分，每个部分的长度K为 16，对应地，自相关窗的长度为 32。增加相关窗长度的方式：可将短训练符号分为5个相同的部分，每个部分的长度为2K，其中，K=16，则2K=32，对应的自相关窗长度就为64。进行同步初始化之后，通过迭代执行计算，前后2种方式的计算复杂度几乎相同，所以本文只考虑自相关窗长度为32的情况。从定量的角度采用阈值比率来衡量各个算法阈值设置的灵活性。考虑2种不同的系统检测性能：1）当PF=PM=10−3时，Minn算法的ηF和ηM分别近似等于0.60和0.83，ρ=1.38。而Pro算法的ηF和ηM分别近似等于1.50和5.10，此时，ρ=3.4；2）当PF=PM=10−4时，Minn算法的ηF和ηM分别近似等于0.65和0.80，ρ=1.33，选择阈值更为有限。而Pro算法的ηF和ηM分别近似等于1.90和 4.20，从而ρ=2.21，可见阈值η仍然有较大的选择余地。

图5AWGN信道下4种算法的FAP和MDP曲线

为获得较精确的阈值设置，可以通过在AWGN信道下进行数值模拟实验，从而获得FAP和MDP曲线。然而为了使FAP和MDP曲线较为平滑，需要大量的数值模拟，少量的模拟次数会使曲线出现波动。与Minn算法相比，Pro算法对仿真FAP和MDP的曲线波动有着更高的容忍度，这一性质可以更容易地选择出合适的阈值。由此可知，比率越大，意味着FAP和MDP在允许范围内有更好的折衷。

图 6显示了在SNR=10 dB 及K=16下，不同CFO值对MoD和Pro算法中归一化因子的影响。ε= 0时，MoD算法表现出最佳性能。但是，当CFO不可忽略时（如ε=0.01），MoD算法的数据分组检测性能显著下降。正如文献[10]所述，MoD算法并不适用于 CFO较大的系统。相反地，对于Pro算法，在ε=0和ε=0.01这2种情况下，MDP曲线是重合的，这充分体现了该算法独立于CFO的特性。

图6不同频偏对MoD和Pro算法检测性能的影响

图7表示的是在AWGN和多径Rayleigh衰落信道下，SNR处于较大范围内变化时，Pro算法的数据分组检测性能曲线。每一次实验中，未知的CFO都设置成一个随机变量，取值为任意实数。其中，软件仿真使用的信道为IEEE802.11含有10个抽头的多径信道[13]，由图7可看到在AWGN和CHI信道下，不同的SNR值（如5 dB、10 dB和15 dB）所对应的MDP曲线几乎是重叠在一起的，这是因为对应于图 3(a)中的峰值平台部分不受多径的影响，在ISI区域内的定时度量函数值在多径Rayleigh衰落信道下只受到噪声的影响，其效果类似于AWGN信道下的情形。

图7AWGN和Rayleigh衰落信道下Pro算法的FAP和MDP曲线

5 结束语

本文主要针对 AWGN信道探讨了一类基于自相关特性的新型归一化因子，提出了一种基于Wi-Fi的D2D突发通信数据分组检测算法。提出的算法独立于系统频偏，因此它无需预先估计系统的频偏，且在同步性能方面可以逼近最优MoD算法，阈值的选择范围较大，易于设置，能很好地实现MDP和FAP之间的折衷，适用于SNR动态变化范围较大的系统。此外，多径Rayleigh衰落信道的阈值选择可由 AWGN的情形中直接得出，无需再进行大量的数值仿真。

式(9)和式(10)的推导。

不失一般性，此处假设θ=0，由式(4)，ϒ(d)可表示为

1) 对d＞0，有y( d−K)=0和y( d)=0，则

因为w( n)和w( n−K )是复高斯噪声样本，且相互独立，它们相乘构成的式子也服从高斯分布，期望为E[w( n) wH(n−K)]=0，方差为则服从瑞利分布，其均值可近似为

2) 对0≤d≤K−2，有y( d−K)=0，而y( d)≠0，则

3) 对K−1≤d≤2K−2，有y( d−K)≠0且y( d)≠0则

其中，假设y( n)和y( n−K )相互独立，并且有相同的方差，那么，的均值为，它的方差为，从而可知服从莱斯分布，其均值可近似为这里，莱斯分布中莱斯因子[14]的各个参数别为，以及表示拉格朗日多项式[15]，对，它可表示为

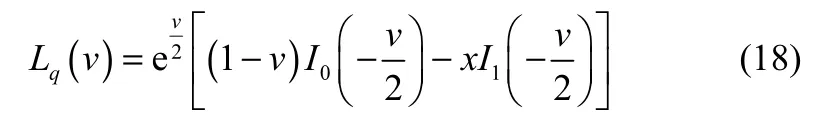
其中，Iα(·)是修正的第一类α阶贝塞尔函数。4) 对2K−1≤d≤PK−1，有y(d−K)≠0且y(d)≠0则得到

5)对PK≤d≤(J+1)K−1，有y(d−K)≠0且y(d)≠0。ϒ(d)与式(19)有相同的形式，服从莱斯分布，其均值可近似为。其中，6) 对于其余的d值，即(J+1)K≤d ，有y( d−K)≠0且y( d)≠0，ϒ(d)有形如式(19)一样的表达式，服从莱斯分布，

[1]CAMPS D M, GARCIA-SAAVEDRA A, SERRANO P. Deviceto-device communications with Wi-Fi direct: overview and experimentation[J]. IEEE Wireless, 2013, 20(3): 96-104.

[2]MACH P, BECVAR Z, VANEK T. In-band device-to-device communication in OFDMA cellular networks: a survey and challenges[J].IEEE Communications Surveys amp; Tutorials, 2015, 17(4): 1885-1922.

[3]ASADI A, WANG Q, MANCUSO V. A survey on device -to-device communication in cellular networks[J]. IEEE Communications Surveys Tutorials, 2014, 16(4): 1801-1818.

[4]CHUNG Y L, LIN M Y. A power-saving resource allocation algorithm for D2D-assisted cellular networks[C]//The 4th IEEE International Conference on Innovative Computing Technology. 2014.

[5]周斌, 胡宏林. 提高蜂窝网络中数据分发效率的 D2D协作转发算法[J]. 电子与信息学报,2012, 34(3): 704-709.ZHOU B,HU H L. Cooperative device-to-device (D2D) forwarding algorithms for improving data dissemination efficiency in cellular networks[J]. Journal of Electronics amp; Information Technology, 2012,34(3): 704-709.

[6]康小磊, 季新生, 黄开枝. 基于人工噪声辅助的D2D异构蜂窝安全通信方法[J]. 通信学报, 2015, 36(10): 1-7.KANG X L, JI X S, HUANG K J. Secure D2D underlaying cellular communication based on artificial noise assisted[J]. Journal on Communications, 2015, 36(10): 1-7

[7]SCHMIDL T, COX D. Robust frequency and timing synchronization for OFDM[J]. IEEE Transactions on Communications, 1997, 45(12):1613-1621.

[8]MINN H, ZENG M, BHARGAVA V. On timing offset estimation for OFDM systems[J]. IEEE Communications Letters, 2000, 4(7): 242- 244.

[9]AWOSEYILA A, KASPARIS C, EVANS B. Robust time-domain timing and frequency synchronization for OFDM systems[J]. IEEE Transactions on Consumer Electronics,2009,55(2):391-399.

[10]ZHANG J, HUANG X. Autocorrelation based coarse timing with differential normalization[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 526-530.

[11]IEEE standard for Information technology-telecommunications and information exchange between systems local and metropolitan area networks-Specific requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications[S]. Std,March 2012.

[12]MINN H, BHARGAVA V, LETAIEF K. A robust timing and frequency synchronization for OFDM systems[J]. IEEE Transactions on Wireless Communications, 2003, 2(4): 822-839.

[13]WANG C L, WANG H C. On joint fine time adjustment and channel estimation for OFDM systems[J].IEEE Transactions on Wireless Communications, 2009, 8(10): 4940-4944..

[14]RICE S O. Mathematical analysis of random noise[J]. Bell System Technical Journal, 1944,23(3): 282-332.

[15]CHAI C C, TJHUNG T T. Unified laguerre polynomial-series-based distribution of small-scale fading envelopes[J]. IEEE Transactions on Vehicular Technology, 2009, 58(8): 3988-3999.

Anti-frequency-shift packet detection for D2D power-saving communications over Wi-Fi network

YANG Fan1, LIANG Xi1, LONG Ke-yu2, JIANG Li2
(1.School of Communication and Information Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China;2.The Second Research Institute of Civil Aviation Administration of China, Chengdu 610041,China)

An efficient packet detection scheme based on Wi-Fi interface was proposed. It was implemented by employing a novel normalized factor as a denominator in OFDM symbol synchronization-timing metric. Compared to the old-tradition schemes, the proposed scheme can not only obtain great detection probability, but also achieve the threshold setting without pre-estimation of frequency offset. Both theoretical analysis and conducted simulation results show that the new scheme facilitates threshold selection for a wide range of signal-to-noise ratio (SNR) in additive white Gaussian noise (AWGN) channel. Besides, the threshold setting in multi-path Rayleigh fading channels can be determined according to the AWGN case straight forwardly.

green communication, device-to-device, OFDM synchronization, Wi-Fi, mobile wireless network

s:The National Natural Science Foundation of China(No.61301272, No.61675040), The Applied Basic Research Foundation of Science and Technology Department of Sichuan Province(No.2014JY0037)

TN92

A

10.11959/j.issn.1000-436x.2016195

2016-03-26；

2016-08-31

国家自然科学基金资助项目（No.61301272，No.61675040）；四川省应用基础研究计划基金资助项目（No.2014JY0037）

杨帆（1982-），男，重庆人，博士，电子科技大学副教授、硕士生导师，主要研究方向为无线移动通信、电力线载波通信、5G关键技术、无人机通信和室内定位。

梁溪（1992-），男，广西贺州人，电子科技大学硕士生，主要研究方向为无线移动通信、室内定位。

龙柯宇（1981-），男，四川乐山人，博士，中国民用航空局第二研究所工程师，主要研究方向为信号处理。

蒋李（1985-），男，四川安岳人，中国民用航空局第二研究所工程师，主要研究方向为电子与通信工程。