永磁型无轴承电机自适应振动抑制控制

张 涛， 倪 伟， 莫丽红， 贾红云

(1. 淮阴工学院 自动化学院，江苏 淮安 223003； 2. 南京信息工程大学 信息与控制学院，南京 210044)



永磁型无轴承电机自适应振动抑制控制

张 涛1， 倪 伟1， 莫丽红1， 贾红云2

(1. 淮阴工学院 自动化学院，江苏 淮安 223003； 2. 南京信息工程大学 信息与控制学院，南京 210044)

为解决在永磁型无轴承电机转子抑制振动控制时，高频噪声信号降低振动信号频率辨识精度，导致系统不稳定的难题，介绍了一种基于多频率跟踪算法的转子自适应振动抑制控制策略。分析了振动信号频率辨识误差形成机理，推导了自适应多频率跟踪算法，构建了转子振动抑制控制系统，采用李雅普诺夫稳定性理论分析了自适应多频率跟踪算法和基于该算法的振动抑制控制系统稳定性。将其应用到永磁型无轴承电机转子磁场定向控制系统中，进行了仿真和实验研究。研究结果表明，自适应多频率跟踪算法可快速准确辨识振动信号频率，基于该方法的振动抑制控制系统，可有效抑制转子振动，提高转子旋转精度。

永磁型无轴承电机；无轴承电机；振动抑制；质量不平衡；自适应控制

永磁型无轴承电机具有无摩擦、无磨损和高功率密度、高转速等独特优点，可实现电机高速高精运行，在涡轮分子泵、离心压缩机、飞轮储能、航空航天等高速直接驱动领域具有广阔的应用前景[1-4]。

由于转子叠片质量分布不均匀、径向位移传感器测量误差、转轴弯曲变形和加工装配精度等原因，导致转子旋转惯性轴与几何中心轴不重合，会产生如下问题：① 电机产生不平衡的偏心磁拉力，引起转子周期性振动，加剧电机的振动和噪声，降低了转子的旋转精度；② 由偏心离心力产生不平衡振动，且振动幅值会随着转速的升高而非线性增大，特别是转子高速旋转时，定、转子将发生摩擦，使系统失控；③ 振动降低了转子刚度，损坏永磁转子结构，使永磁型无轴承电机转速和功率的进一步提升受到限制，严重影响系统动态特性和安全运行[5-6]。

文献[7]分析了永磁型无轴承电机不平衡振动特性，推导出转子振动方程，提出了在振动控制方法中最具代表性的“前馈补偿控制策略”。文献[8]采用基于最小均方算法的自适应凹陷滤波器对无轴承开关磁阻电机转子质量偏心进行补偿控制。此后，又有学者提出采用重复控制和模糊控制策略对悬浮转子振动进行控制，从现有文献可以看出，所有振动控制策略的关键是准确、实时在线辨识振动信号频率[9-10]，但控制系统中不可避免的存在高频噪声信号，信号辨识模型不可能全部滤除高频噪声信号。因此，振动信号频率辨识产生误差，由此频率信号构成的转子振动控制系统转子旋转精度较低，降低了电机动态特性，误差较大时，将导致控制系统不稳定，这些控制方法的实际应用受到极大限制。

本文以准确辨识转子振动信号频率为核心，分析了振动信号频率估算误差形成机理，提出了基于多频率跟踪算法的永磁型无轴承电机转子自适应抑制振动控制策略，推导了多频率跟踪算法，采用李雅普诺夫稳定性理论证明其稳定性，构建了永磁型无轴承电机转子振动补偿控制系统，并进行仿真和实验研究，结果表明，该方法能够准确辨识振动频率，抑制转子振动，减小旋转时的转子振幅，提高了转子的旋转精度。

1 抑制振动控制机理

图1所示的是无轴承电机转子振动抑制机理，假设转子角速度为ω，由于转子存在质量偏心等原因，径向位移传感器检测到的信号x和y为正弦信号，且相位相差90°，旋转产生的离心力fu欲使转子围绕惯性中心轴旋转，而位移闭环控制器将产生相应的不平衡磁拉力f，试图使转子围绕几何中心轴旋转，根据作用力与反作用力原理，转子将产生径向振动，振动将传递到定子与机座，引起系统振动，当振动频率等于系统固有频率时，将产生共振。

图1 振动抑制机理Fig.1 Mechanism of vibration-rejection

利用悬浮转子刚度和阻尼可调节的特点，可采用控制策略降低或者消除转子振动，即产生一个与转子振动信号幅值大小相等、相位相反的信号，抵消位移闭环控制系统中误差信号中的振动信号，径向位移闭环控制系统不控制转子振动信号，即不产生不平衡磁拉力f，从而减小或消除了振动力。由于质量偏心远小于电机气隙长度，在转子振动抑制控制时，总可以使转子围绕其惯性中心轴旋转而无振动力传递到定子与机座上，彻底消除转子振动，特别适合应用于无轴承电机系统的转子振动抑制。

2 振动信号频率辨识

转子位移传感器的输出信号由位移信号、振动信号和高频噪声信号组成。振动信号包括转子质量不平衡信号与位移传感器误差信号[11-12]，高频噪声信号可表示为：

(1)

式中：ωi、αi、βi分别为有色噪声i的频率和幅值，rand(t)为白噪声序列。

假设振动信号由多频率信号组成：

(2)

式中：ωdj、αdj、βdj分别为振动信号j的频率和幅值。

位移控制系统的扰动信号为：

d=Nz+Nd

(3)

与噪声信号相比，当i=j时，αi≪αdj，βi≪βdj，ωdj≪ωi(i=1,…,M)。

振动信号辨识模型的输出信号为：

(4)

式中：ωj为输出信号频率，αj、βj为输出信号幅值。

图2所示的是单自由度转子振动抑制控制框图。假设控制器、驱动和悬浮系统的传递函数为G(s)=Aejθ，与振动信号r相比，让y*-y=0，则系统稳态输出y为：

y=rG(jω)=

(5)

式中：Aj，θj为系统频率为ωj时的增益和相位，则系统稳态输出误差e为：

e=y+d=

αdj(t)sin(ωdjt)+βdj(t)cos(ωdjt)}+Nd

(6)

e经过振动信号辨识模型，提取出振动信号。

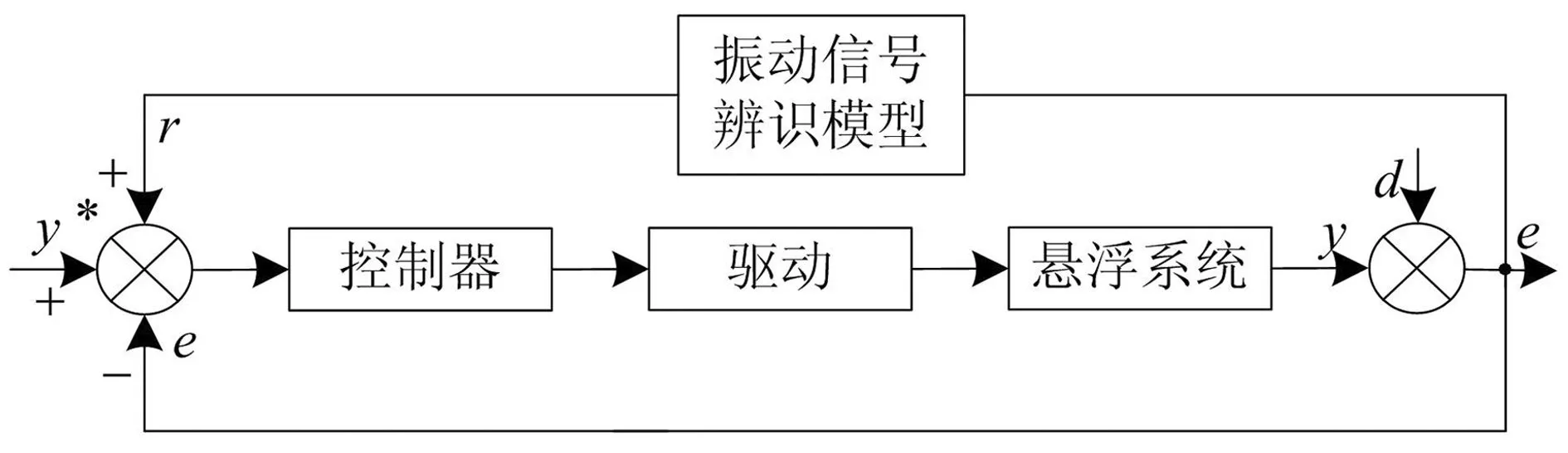
图2 振动抑制控制框图Fig.2 Block diagram of vibration-rejection control

振动信号辨识原理如图3所示，包括信号分解、傅里叶系数计算和信号合成三部分[13]。

图3 振动信号辨识模型Fig.3 Identification model of vibration signal

信号分解过程如图4所示，e分别与正弦和余弦信号相乘可得：

(7)

求解可得：

βj(t)cos(ωjt+θj)]sin(ωjt)+[αdj(t)sin(ωdjt)+

βdj(t)cos(ωdjt)]sin(ωjt)}+Ndsin(ωjt)=

βj(t)(sin(2ωjt+θj)-sinθj)]+

0.5[αdj(cos(ωdj-ωj)t-cos(ωdj+ωj)t)+

βdj(sin(ωdj-ωj)t-sin(ωdj+ωj)t)]+Ndsin(ωjt)}(8)

图4 输入信号分解Fig.4 Decomposition of input signals

低通滤波器截止频率定义为ωBj，ωBj≥2ωdj。高频噪声信号频率ωi远大于滤波器的截止频率ωBj。所以，经过低通滤波器后，高频噪声信号被滤除。

定义频率辨识误差为：

Δω=ωdj-ωj

(9)

低通滤波器输出信号为：

(10)

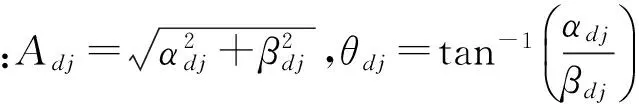
当Δω=0时，采样自适应律与频率ωj无关。

(11)

式中:μ1j，μ2j为采样步长，所以

式中:

(13)

上式为非线性自适应律，对于不同的θj，当初值μj满足一定条件时，非线性系统稳定。

但低通滤波器不可能全部滤除高频信号，造成频率估算存在误差，即Δω≠0时，式(10)的离散形式为：

0.5Adj[sin(Δω(k+1)+θdj)]}=

(βj(k)-μ2j(k+1)n2j(k))sinθj+

0.5Adj[sin(Δω(k+1)+θdj)]}

(14)

由于Δω≪ωj，则cosΔω≅1，sinΔω≅Δω，上式可写为：

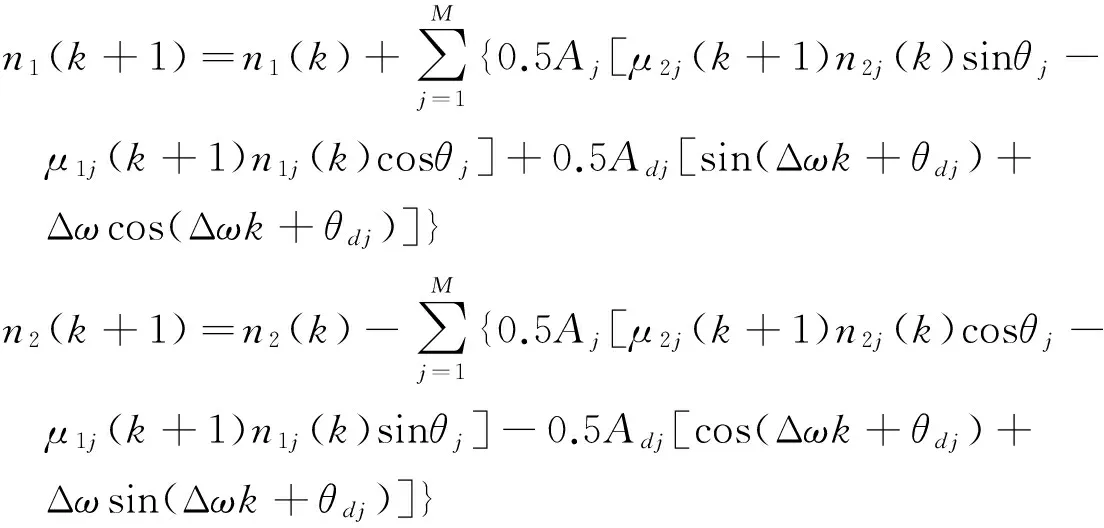
n1j(k+1)和n2j(k+1)不仅与n1j(k)和n2j(k)有关，还与频率辨识误差Δω有关，因此，对于上式所示的非线性系统，即使选择合适的初值μ1j和μ2j(j=1，…，M)，也不能保证其稳定，所以很有必要修正频率辨识算法，提高频率辨识精度。

3 多频率自适应跟踪算法

由式(10)可得：

Nj(t)=n1j(t)+n2j(t)=

0.5Aj[αj(t)(cosθj+sinθj)+βj(t)(cosθj-sinθj)]+

0.5Adj[sin(Δω+θdj)+cos(Δω+θdj)]

(16)

Nj(k)的离散形式为：

Nj(k+1)=

Nj(k)+0.5Aj[μ1j(k+1)n1j(k)(cosθj+sinθj)+

μ2j(k+1)n2j(k)(cosθj-sinθj)]+

0.5AdjΔω[cos(Δω(k+1)+θdj)-

sin(Δω(k+1)+θdj)]=0.5Nj(k)+

0.5AdjΔω[cos(Δωk+θdj)-sin(Δωk+θdj)]

(17)

当k→∞时，Δω必须为零，可得修改后的自适应律为：

ωj(k+1)=ωj(k)-μ3j(k+1)Nj(k)

(18)

式中：

采用输出信号Nj(t)修正估算频率，频率辨识结果趋近实际值[11,13-14]。

4 稳定性分析

4.1 算法稳定性

式(11)描述的自适应律参数αj、βj与θj无关，假设Nj(k+1)=n1j(k+1)+n2j(k+2)，由式(12)可得：

Nj(k+1)=Nj(k)-0.5Aj[(μ2j(k+1)n2j(k)+

μ1j(k+1)n1j(k))(cosθj+sinθj)

(20)

定义μj(k+1)Nj(k)=μ2j(k+1)n2j(k)+μ1j(k+1)n1j(k)，则，

μj(k+1)=(μ2j(k+1)n2j(k)+

μ1j(k+1)n1j(k))/Nj(k)

(21)

(22)

则式(20)可写为：

Nj(k+1)=Nj(k)-

0.5Aj[(μj(k+1)Nj(k)(cosθj+sinθj)]

(23)

V(k+1)-V(k)=N2(k+1)-N2(k)=

0.5Adj[sin(Δωj(k+1)+θdj]}=

0.5Ajμj(k+1)Nj(k)(cosθj+sinθj)]2}≤

(24)

4.2 控制系统稳定性

由式(10)可得

则

Nj(k+1)=n1j(k+1)+n2j(k+1)=0.5Nj(k)+

0.5AdjΔω[cos(Δωk+θdj)-sin(Δωk+θdj)]

(26)

定义：ΔNj(k+1)=Nj(k+1)-Nj(k)。则李雅普诺夫函数为[16-17]：

Vj(k+1)-Vj(k)=Nj(k+1)2-Nj(k)2=

2ΔNj(k+1)Nj(k)+ΔNj(k+1)2

(27)

当上式等号右边小于零时，控制系统稳定。

Vj(k+1)-Vj(k)=

2[-0.5Nj(k)+0.5AdjΔω(cos(Δω+θdj)-

sin(Δω+θdj))]Nj(k)+[-0.5Nj(k)+

0.5AdjΔω(cos(Δω+θdj)-sin(Δω+θdj))]2=

-0.75Nj(k)2+0.5Nj(k)ΔωAdj[cos(Δωk+θdj)-

sin(Δωk+θdj)]2

(28)

(29)

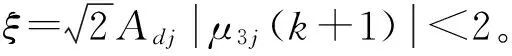
因此，上式小于等于零的条件是，μ3j的初值满足

(30)

因此，选择合适的初值，控制系统渐近稳定，频率估算值趋近实际值。

5 仿真与实验研究

为验证算法的正确性，给出由频率为f1=105 Hz和f2=306 Hz的正弦信号、有色噪声和白噪声组成的混合信号，其波形如图5(a)所示。采用不考虑辨识误差的振动信号自适应辨识模型从合成信号中辨识出的振动频率分别为f1=103.061 1 Hz，f2=304.761 5 Hz。而采用基于多频跟踪算法的振动信号自适应辨识模型，从合成信号中辨识出的振动频率结果如图5(b)和5(c)所示，分别为f1=104.998 2 Hz，f2= 305.995 1 Hz，频率辨识误差小于0.18%。

图5 自适应多频率跟踪算法仿真结果Fig.5 Simulation results of adaptive multi-frequency tracking algorithm

永磁型无轴承电机实验样机参数为：转子质量m=1.25 kg，转动惯量J=2.3×10-4kg·m2，转矩绕组极对数PM=1，悬浮绕组极对数PB=2，转矩绕组电阻为2.5 Ω，悬浮绕组电阻为1.9 Ω，定子外径为120 mm，转子外径为65 mm，定子内径为67 mm，永磁体厚度1 mm，铁心长度为85 mm，气隙厚度为1 mm，定子槽数24，辅助轴承厚度0.5 mm，永磁体剩余磁感应强度为1.2 T，悬浮力绕组匝数NB=30，永磁体矫顽力为900(kA/m)，转矩绕组匝数NM=35，转速设定为6 000 r/min，经实验测得转子偏心距ρ=5 μm，在建立永磁型无轴承电机控制模型时，在转子径向位移模型中叠加随机白噪声信号作为高频噪声信号，建立永磁型无轴承电机转子抑制振动控制系统框图如图6所示。

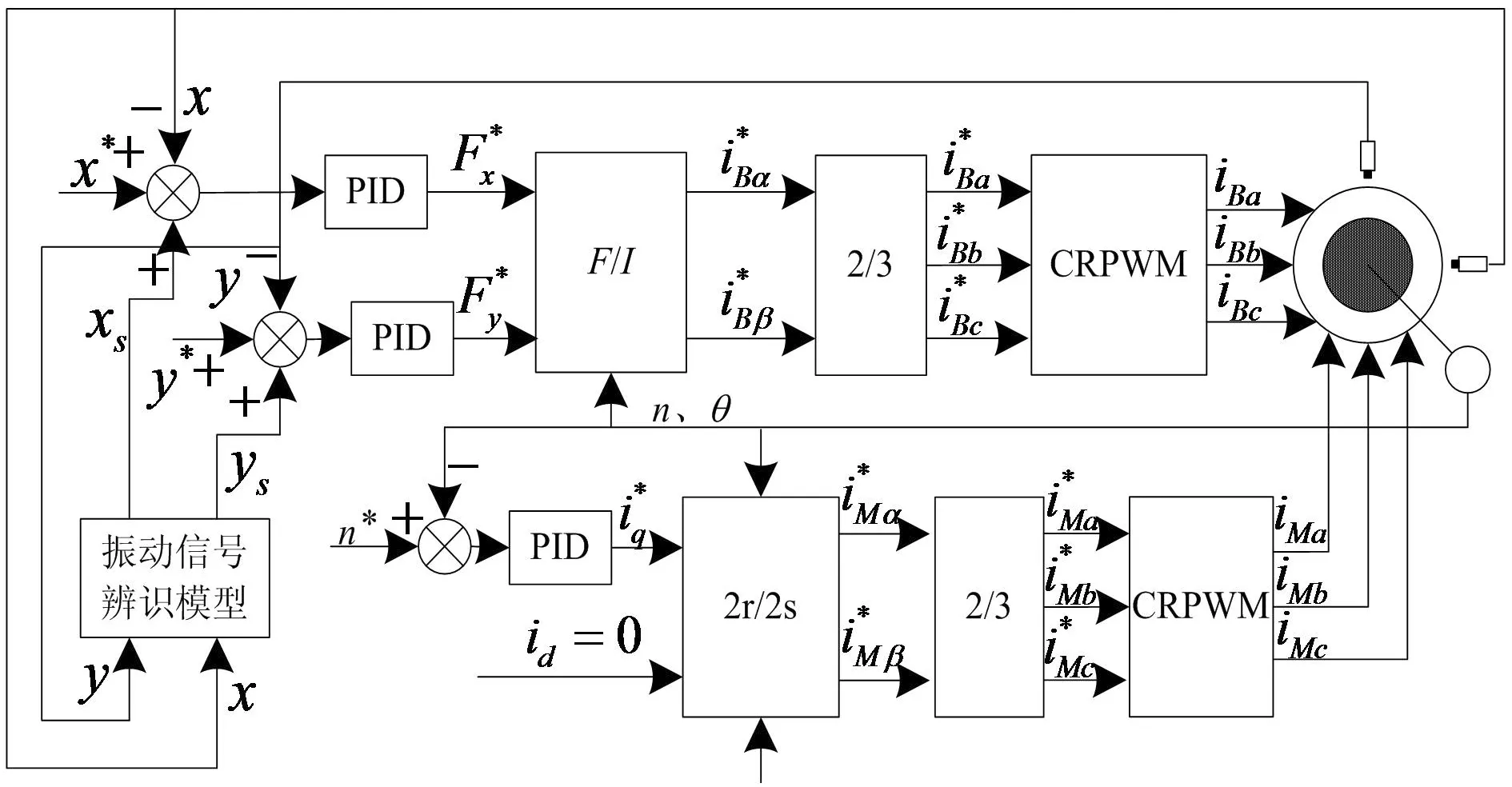
图6 永磁型无轴承电机转子自适应振动控制框图Fig.6 The block diagram of adaptive rotor vibration control system for permanent magnet-type bearingless motor

仿真结果如图7所示，在稳定运行状态，图7(a)是对转子振动不加控制时的转子旋转轨迹波形，转子在x和y方向的振动位移相等，约为100 μm；图7(c)是采用传统振动信号自适应辨识模型的振动方法时，转子在y方向的位移波形，约为25 μm。图7(d)是基于多频率跟踪算法的自适应辨识模型振动控制方法时，转子在x方向位移波形，约为4 μm，对应的转子旋转轨迹如图7(b)所示。由仿真结果可知，由于振动信号频率估算存在误差，使得基于传统自适应律的永磁型无轴承电机转子振动控制策略的转子振动效果为原幅值的25%，而采用多频率跟踪算法的振动控制策略可以将转子径向振动降低为原幅值的4%，提高转子旋转精度，转子围绕惯性中心旋转。

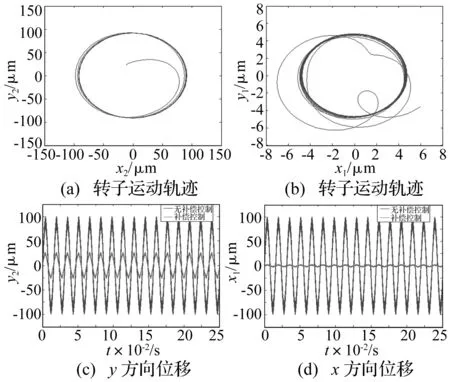
图7 仿真结果Fig.7 Simulation results

1.逆变器; 2.直流电源；3. 交流电源；4.旋转编码器；5.永磁型无轴承电机；6. 位移传感器；7. 接口电路；8.DSP控制板图8 实验样机与实验平台Fig.8 Experimental prototype motor and platform

试制了一台永磁型无轴承电机，建立了实验平台，如图8所示，控制系统由实验样机、位移传感器、旋转编码器、位移和转速接口电路、驱动电路及控制器组成。实验结果如图9所示，图9(a)给出的是采用传统振动信号自适应辨识模型时的转子几何中心运动轨迹，振幅约为40 μm；图9(b) 所示的是基于多频率跟踪算法的自适应辨识模型振动控制方法时，转子几何中心旋转轨迹，振幅约为5 μm。从实验结果可以看出，由于采用了高辨识精度的多频率跟踪算法，极大地抑制了位移闭环控制系统中的振动信号，转子围绕惯性中心旋转，彻底消除转子振动。

图9 实验结果Fig.9 Experimental results

6 结 论

为提高永磁型无轴承电机转子旋转精度和动态特性，在分析转子振动信号频率辨识误差形成机理的基础上，研究一种可准确辨识振动频率的多频率跟踪算法，将其加入到永磁型无轴承电机转子磁场定向控制系统中，采用李雅普诺夫稳定性理论分析其稳定性，并进行仿真和实验研究，得出如下结论：

(1) 多频率跟踪算法提高了振动信号频率辨识精度；

(2) 基于多频率跟踪算法的永磁型无轴承电机控制系统可有效抑制转子振动，使转子围绕其惯性轴旋转;

(3) 该算法不受振动信号来源的影响，可应用于抑制其他结构的无轴承电机转子振动。

[1] 王凤翔. 高速电机的设计特点及相关技术研究[J]. 沈阳工业大学学报, 2006, 28(3):258-264.WANG Fengxiang. Study on design feature and related technology of high speed electrical machines [J].Journal of Shenyang University of Technology, 2006, 28(3): 258-246.[2] 王继强, 王凤翔, 鲍文博,等. 高速永磁电机转子设计与强度分析[J].中国电机工程学报, 2005, 25(15):2843-2848.

WANG Jiqiang, WANG Fengxiang, BAO Wenbo, et al. Rotor design and strength analysis of high speed permanent magnet machine[J]. Proceedings of the CSEE, 2005, 25(15): 2843-2848.

[3] NASIR M, UDDIN U. Control of interior type PM synchronous motor for high speed operations-summary [J]. Power Engineering Society General Meeting, 2004, 2：1280-1283.

[4] SCHNEIDER T, BINDER A. Design and evaluation of a 60 000 r/min permanent magnet bearingless high speed motor[J]. IEEE Transactions on Industry Applications,2006,42(4): 1031-1037.

[5] BINDER A, SCHNEIDER T, KLOHR M. Fixation of buried and surface-mounted magnets in high-speed permanent-magnet synchronous machines[J]. IEEE Transactions on Industry Applications, 2006, 42(4): 1031-1037.

[6] ELNAZ V, BAHRAM S, STUART B. Estimation and rejection of unknown sinusoidal disturbance using a generalized adaptive force balancing method[C]// Proceedings of the 2007 American control conference.New York, USA, 2007: 3529-3534.

[7] 张涛，朱熀秋. 无轴承永磁同步电机转子质量不平衡补偿控制[J]. 中国电机工程学报, 2007, 27(15): 33-37.

ZHANG Tao, ZHU Huangqiu. Rotor’s mass unbalance compensation control in bearingless permanent magnet-type synchronous motors [J]. Proceedings of the CSEE,2007,27(15): 33-37.

[8] 张倩影, 邓智泉, 杨艳. 无轴承开关磁阻电机转子质量偏心补偿控制[J]. 中国电机工程学报,2011,31(21): 128-134.ZHANG Qianying, DENG Zhiquan, YANG Yan. Compensation control of rotor mass eccentric in bearingless switched reluctance motors [J]. Proceedings of the CSEE, 2011, 31(21): 128-134.

[9] ALEKSANDAR B, HENK P, JAN A F. On the speed limits of permanent magnet machines [J]. IEEE Transactions on Magnetics, 2010, 57(1): 220-227.

[10] SUNG I K, YOUNG K K, GEUN H L, et al. A novel rotor configuration and experimental verification of interior PM synchronous motor for high speed applications [J]. IEEE Transactions on Magnetics, 2012, 48(2): 843-846.

[11] JIANG Kejian, ZHU Changsheng. Multi-frequency periodic vibration suppressing in active magnetic bearing-rotor systems via response matching in frequency domain[J].Mechanical Systems and Signal Processing, 2011, 25 : 1417-1429.

[12] NONAMI K, FAN Q. Unbalance vibration control of magnetic bearing systems using adaptive algorithm with disturbance frequency estimation[C]// Proceedings of the 6th International Symposium on Magnetic Bearings.Cambridge, MA, 1998, 663-672.

[13] SHI J, MOOD R Z, QIN L. Synchronous disturbance attenuation in magnetic bearing systems using adaptive compensating signals[J]. Control Engineering Practice, 2004, 12 :283-290.

[14] TSAI N C, SHIH L W, LEE R M. Spindle vibration suppression for advanced milling process by using self-tuning feedback control[J]. International Journal of Advanced Manufacture Technology, 2010, 48: 1-10.

[15] XIANG Min, WEI Tong. Autobalancing of high-speed rotors suspended by magnetic bearings using LMS adaptive feedforward compensation[J]. Journal of Vibration and Control, 2014, 20(9): 1428-1436.

[16] YOON S Y, LIN Z L, ALLAIRE P E. Control of surge in centrifugal compressors by active magnetic bearings [M]. London: Springer-Verlag, 2013.

[17] KEUCHEL U, STEPHAN R M. Microcomputer based adaptive control applied to thyristor-driven DC Motors[M]. London: Springer-Verlag, 1994.

Adaptive vibration-rejection control on permanent-magnet-type bearingless motors

ZHANG Tao1, NI Wei1, MO Lihong1, JIA Hongyun2

(1. Faculty of Automation, Huaiyin Institute of Technology, Huai’an 223003, China；2. School of Information and Control Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, China)

This work aims to solve the issues that the high frequency noise signal seriously affects the identification precision of vibration frequency and that the vibration-rejection control system is unstable in permanent-magnet-type bearingless motor. A vibration-rejection control method based on adaptive multi-frequency tracking algorithm was presented. The mechanism of vibration frequency identification error was analyzed. The adaptive multi-frequency tracking algorithm was induced and the control system was constructed. Using Lyapunov stability theory, the adaptive multi-frequency tracking algorithm and the control system asymptotically stability were proved. The method was added into the rotor field oriented control system of permanent-magnet-type bearingless motor. Simulation and experiments were conducted. The results show that the adaptive multi-frequency tracking algorithm can identify the vibration frequency quickly and correctly. The vibration-rejection control system can suppress the rotor vibration and the rotational accuracy is improved.

permanent-magnet-type bearingless motor; bearingless motor; vibration-rejection; mass unbalance; adaptive control

江苏省自然科学基金资助项目(BK2012462;BK20130418);江苏省高校自然科学研究项目 (13KJB470001)

2015-06-18 修改稿收到日期：2015-09-23

张涛 男，博士，讲师，1978年11月生

TM301.2

A

10.13465/j.cnki.jvs.2016.20.011