二次函数的极值问题

董晓磊

二次函数的极值问题

董晓磊

二次函数极值问题是中考数学中的热点问题，而利用二次函数求极值又是初中数学中常见的一种手段，本文将结合2015年中考原题具体阐述这类问题.

例1（2015·南京）某企业生产并销售某种产品，假设销售量与产量相等.如图1中的折线ABD、线段CD分别表示该产品每千克生产成本y1（单位：元）、销售价y2（单位：元）与产量x（单位：kg）之间的函数关系.

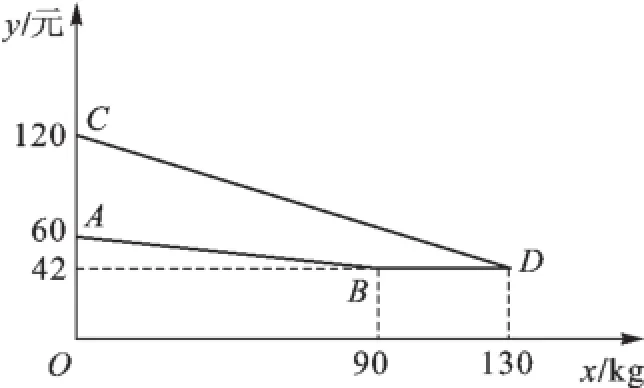
图1

（1）请解释图中点D的横坐标、纵坐标的实际意义；

（2）求线段AB所表示的y1与x之间的函数表达式；

（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

【分析】（1）点D的横坐标、纵坐标的实际意义：当产量为130 kg时，该产品每千克生产成本与销售价相等，都为42元；

（2）根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可；

（3）利用总利润=单位利润×产量列出有关x的二次函数，求得最值即可.

解：（1）点D的横坐标、纵坐标的实际意义：当产量为130 kg时，该产品每千克生产成本与销售价相等，都为42元.

（2）设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1，

∵y=k1x+b1的图像过点（0，60）与（90，42），

∴这个一次函数的表达式为：y=-0.2x+ 60（0≤x≤90）.

（3）设y2与x之间的函数关系式为y= k2x+b2，

∵y=k2x+b2的图像经过点（0，120）与（130，42），

∴这个一次函数的表达式为y2=-0.6x+ 120（0≤x≤130）.

设产量为x kg时，获得的利润为W元，

当0≤x≤90时，W=x［（-0.6x+120）-（-0.2x+60）］=-0.4（x-75）2+2 250，∴当x=75时，W的值最大，最大值为2250；当90≤x≤130时，W=x［（-0.6x+120）-42］=-0.6（x-65）2+2 535，

∴当x=90时，W=-0.6（90-65）2+2 535= 2 160，

由-0.6＜0知，当x＞65时，W随x的增大而减小，∴当90≤x≤130时，W≤2 160.

因此当该产品产量为75 kg时，获得的利润最大，最大值为2 250.

【点评】此题考查了二次函数的应用，解题的关键是从实际问题中抽象出二次函数模型，在自变量不同取值范围内，求出每段的最大值，最后进行比较，得出结论.

例2（2015·济宁）如图2，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y=，与x轴相交于点D，以点C为顶点的抛物线过点B.

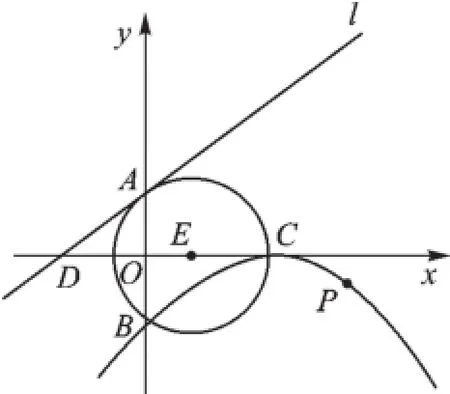
图2

（1）求抛物线的解析式；

（2）判断直线l与⊙E的位置关系，并说明理由；

（3）动点P在抛物线上，当点P到直线l的距离最小时，求出点P的坐标及最小距离.

【分析】（1）连接AE，由已知得：AE=CE= 5，OE=3，利用勾股定理求出OA的长，结合垂径定理求出OC的长，从而得到C点坐标，进而得到抛物线的解析式；

（3）过点P作直线l的垂线段PQ，垂足为Q，过点P作直线PM垂直于x轴，交直线l于点M.

解：（1）如图3，连接AE，由已知得：

AE=CE=5，OE=3，

在Rt△AOE中，由勾股定理得，

图3

∵OC⊥AB，∴由垂径定理得，OB=OA=4，

OC=OE+CE=3+5=8，

∴A（0，4），B（0，-4），C（8，0），

∵抛物线的顶点为C，

∴设抛物线的解析式为y=a（x-8）2，

当x=0时，y=4，

∴点A在直线l上，

在Rt△AOE和Rt△DOA中，

∵∠AOE=∠DOA=90°，

∴△AOE∽△DOA，

∴∠AEO=∠DAO，

∵∠AEO+∠EAO=90°，

∴∠DAO+∠EAO=90°，即∠DAE=90°，因此，直线l与⊙E相切于A.

（3）如图4，过点P作直线l的垂线段PQ，垂足为Q，过点P作直线PM垂直于x轴，交直线l于点M.

图4

∵PM⊥x轴，

∴∠QMP=∠DAO=∠AEO，

又∠PQM=90°，

∴△PQM的三个内角固定不变，

∴在动点P运动的过程中，△PQM的三边的比例关系不变，

∴当PM取得最小值时，PQ也取得最小值，PQ最小=PM最小·sin∠QMP =PM最小·sin∠AEO=

【点评】此题是二次函数综合题，涉及勾股定理、待定系数法求二次函数解析式、切线的判定和性质、二次函数的最值等知识，在解答（3）时要注意点P、点M坐标的设法，以便利用二次函数的最值求解.

例3（2015·东莞）如图5，在同一平面上，两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4 cm.

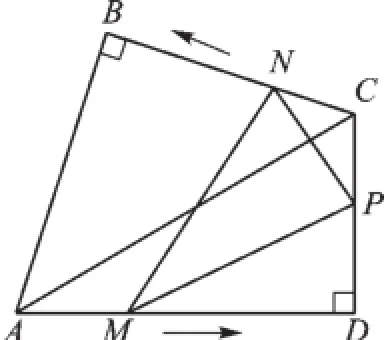
图5

（1）填空：AD=_______（cm），DC= _______（cm）；

（2）点M，N分别从A点，C点同时以每秒1 cm的速度等速出发，且分别在AD，CB上沿A→D，C→B方向运动，求当M，N点运动了x秒时，点N到AD的距离（用含x的式子表示）；

（3）在（2）的条件下，取DC中点P，连接MP，NP，设△PMN的面积为y（cm2），在整个运动过程中，△PMN的面积y存在最大值，请求出y的最大值.

【分析】（1）由勾股定理求出AC，由∠CAD=30°，得出DC=，由三角函数求出AD即可；

（2）过N作NE⊥AD于E，作NF⊥DC，交DC的延长线于F，则NE=DF，求出∠NCF= 75°，∠FNC=15°，由三角函数求出FC，得NE= DF=，即可得出结果；

（3）由三角函数求出FN，得出PF，由△PMN的面积=梯形MDFN的面积-△PMD的面积-△PNF的面积，得出y关于x的二次函数，即可得出y的最大值.

解：（1）∵∠ABC=90°，AB=BC=4 cm，

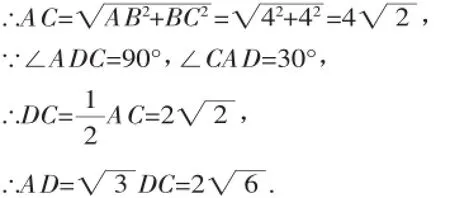
（2）过点N作NE⊥AD于E，作NF⊥DC，交DC的延长线于F，如图6所示：

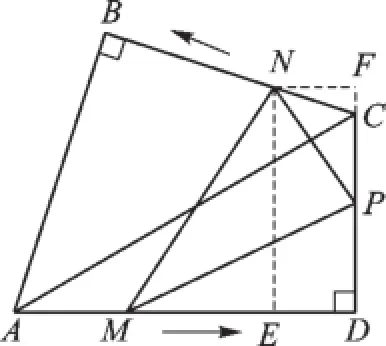
图6

则NE=DF，

∵∠ABC=∠ADC= 90°，AB=BC，∠CAD= 30°，∴∠ACB=45°，∠ACD=60°，

∴∠NCF=180°-45°-60°=75°，∠FNC=15°，

∴FN=

∵△PMN的面积=梯形MDFN的面积-△PMD的面积-△PNF的面积，

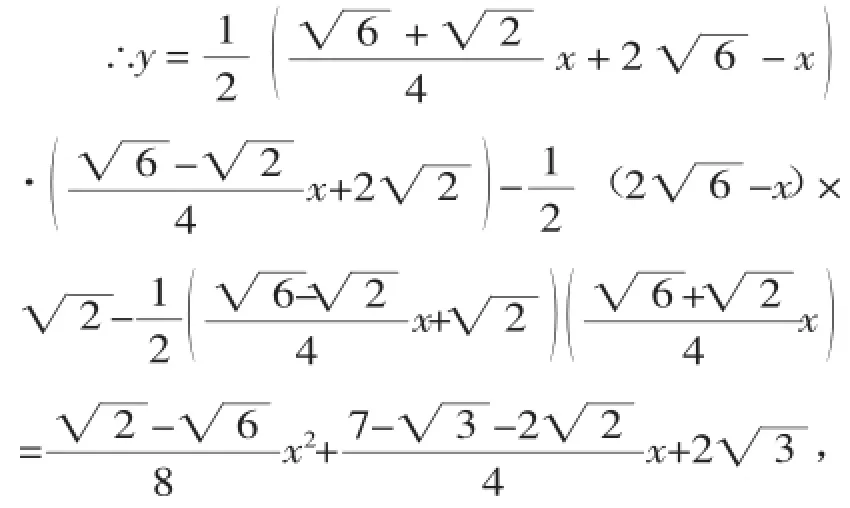
由此可知y是x的二次函数，

【点评】此题是在几何动点问题中利用二次函数求最大值，解题的关键是利用补形的方法表示出三角形的面积.本题难度较大，综合性也很强.

（作者单位：江苏省宿迁市钟吾国际学校）