“函数”复习专题

张志军

“函数”复习专题

张志军

一、选择题

1.二次函数y=-2（x-1）2+3的图像的顶点坐标是（）.

A.（1，3）B.（-1，3）C.（1，-3）D.（-1，-3）

2.将函数y=-3x的图像沿x轴向左平移2个单位长度后，所得图像对应的函数关系式为（）.

A.y=-3x+2B.y=-3x-2C.y=-3（x+2）D.y=-3（x-2）

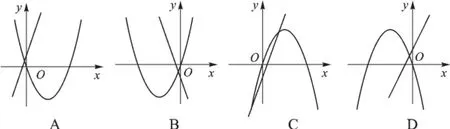
3.在同一平面直角坐标系中，函数y=ax2+bx与y=bx+a的图像可能是（）.

4.如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2，则关于x的不等式-x+ m＞nx+4n＞0的整数解为（）.

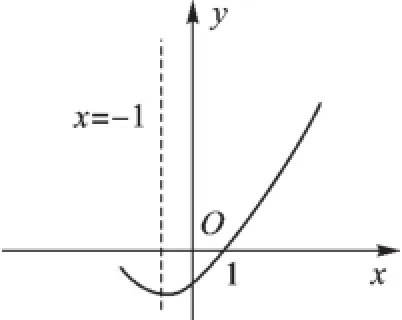
A.-1B.-5C.-4D.-3

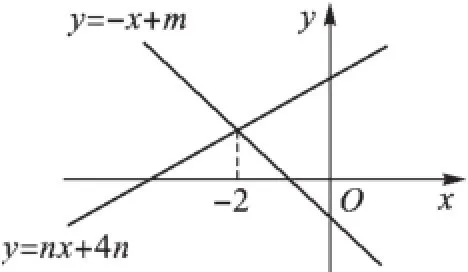
第4题图

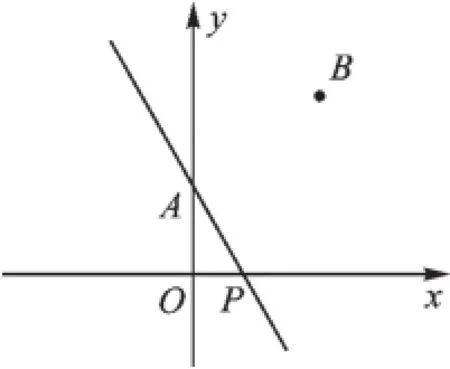
第5题图

第6题图

A.3B.4C.5D.6

6.如图，直线y=x-2与y轴交于点C，与x轴交于点B，与反比例函数的图像在第一象限交于点A，连接OA，若S△AOB∶S△BOC=1∶2，则k的值为（）.

A.2B.3C.4D.6

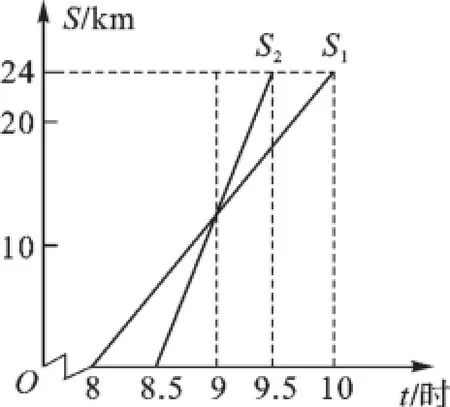
7.小亮家与姥姥家相距24 km，小亮8：00从家出发，骑自行车去姥姥家.妈妈8：30从家出发，乘车沿相同路线去姥姥家.在同一直角坐标系中，小亮和妈妈的行进路程S（km）与北京时间t（时）的函数图像如图所示.根据图像得到结论，其中错误的是（）.

A.小亮骑自行车的平均速度是12 km/hB.妈妈比小亮提前0.5小时到达姥姥家

C.妈妈在距家12 km处追上小亮D.9：30妈妈追上小亮

第7题图

第8题图

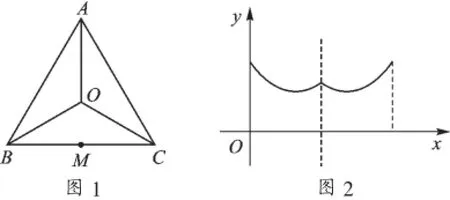
8.一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB，BC，CA，OA，OB，OC组成.为记录寻宝者的行进路线，在BC的中点M处放置了一台定位仪器.设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图像大致如图2所示，则寻宝者的行进路线可能为（）.

A.A→O→BB.B→A→CC.B→O→CD.C→B→O

二、填空题

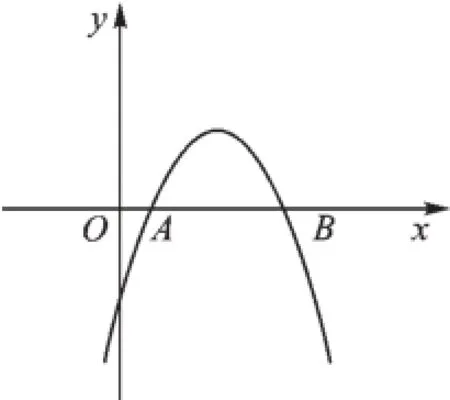
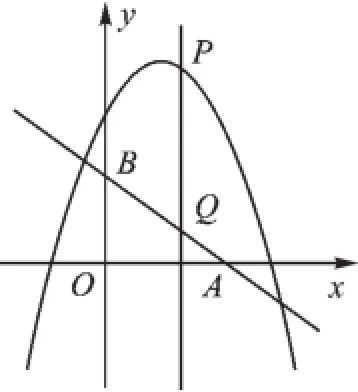
10.如图，是二次函数y=ax2+bx+c（a≠0）的图像的一部分，给出下列命题：

①a+b+c=0；②b＞2a；③a-2b+c＞0；④ax2+bx+c=0的两根分别为-3和1.

其中正确的命题是_______.（只要求填写正确命题的序号）

第10题图

第11题图

11.如图，抛物线y=-x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧.当x=x2-2时，y______0.（填“＞”、“=”或“＜”号）

12.正方形A1B1C1O和A2B2C2C1按如图所示方式放置，点A1、A2在直线y=x+1上，点C1，C2在x轴上，已知点A1的坐标是（0，1），则点B2的坐标为_______.

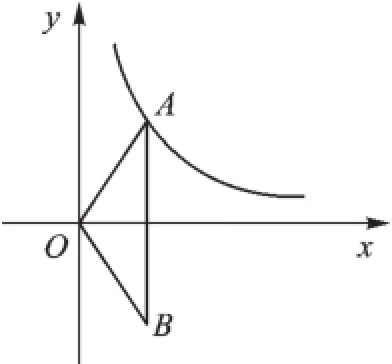
13.如图，点A、B的坐标分别为（0，2），（3，4），点P为x轴上的一点，若点B关于直线AP的对称点B′恰好落在x轴上，则点P的坐标为_______.

第12题图

第13题图

第14题图

三、解答题

（1）判断该函数图像的另一支所在的象限，并求m的取值范围；

（2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图像上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值.

16.如图，隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4 m.按照图中所示的直角坐标系，抛物线可以用表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为

第15题图

第16题图

第17题图

（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；

（2）一辆货运汽车载一长方体集装箱后高为6 m，宽为4 m，如果隧道内设双向车道，那么这辆货车能否安全通过？

（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8 m，那么两排灯的水平距离最小是多少米？

17.已知一次函数y=2x-4的图像与x轴、y轴分别相交于点A、B，点P在该函数图像上，P到x轴、y轴的距离分别为d1、d2.

（1）当P为线段AB的中点时，求d1+d2的值；

（2）直接写出d1+d2的范围，并求当d1+d2=3时点P的坐标；

（3）若在线段AB上存在无数个P点，使d1+ad2=4（a为常数），求a的值.

18.甲、乙两人匀速从同一地点到1 500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图像的一部分如图所示.

（1）求甲行走的速度；

（2）在坐标系中，补画s关于t函数图像的其余部分；

（3）问甲、乙两人何时相距360米？

19.如图，在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线l：y=kx+b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC.

（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）；

第18题图

（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求a的值；

（3）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由.

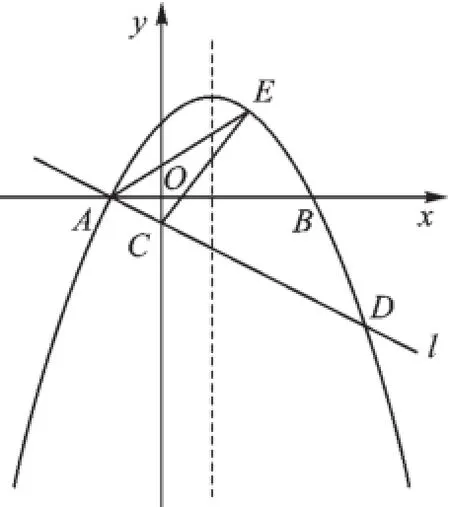
第19题图

备用图

扫二维码关注微信输入“数学”查答案

（作者单位：江苏省宿迁市钟吾国际学校）